An application of zero forcing sets in quantum computing

Özlem Salehi

WGT-Workshop on Graph Theory and Its Applications-X

14.10.2022

OUTLINE

A brief introduction to quantum computing
Quantum Approximate Optimization Algorithm (QAOA)
Zero forcing sets
Universality of QAOA and zero forcing sets
Open questions

Based on: Morales, M.E., Biamonte, J.D. and Zimborás, Z., 2020. On the universality of the quantum approximate optimization algorithm. Quantum Information Processing, 19(9), pp.1-26

BIT vs. QUBIT

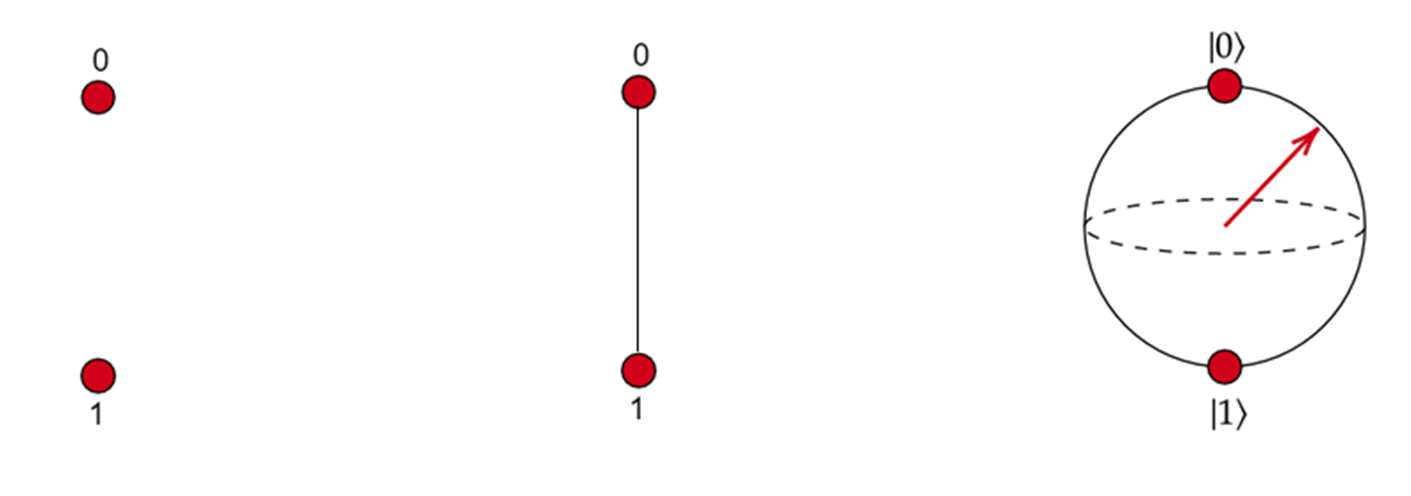
Probabilistic Bit

Bit

Qubit

Either 0 or 1

0 with probability $p_0$

1 with probability $p_1$

$p_0 + p_1 = 1$

$|0\rangle$ with probability $|a_0|^2$

$|1\rangle$ with probability $|a_1|^2$

$|a_0|^2 + |a_1|^2 = 1$

a_0 |0\rangle + a_1 |1\rangle

p_0 [0] + p_1[1]

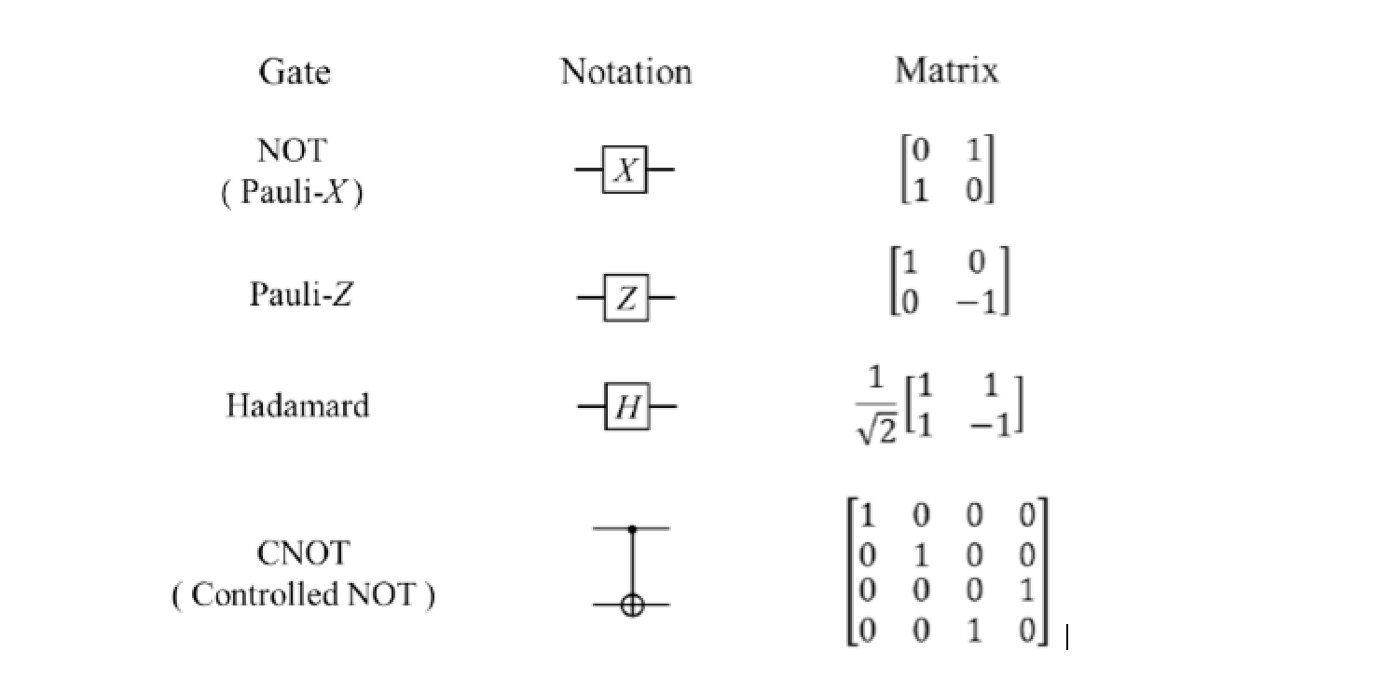
GATE-BASED COMPUTING

Gates corresponding to unitary operators

Measurement

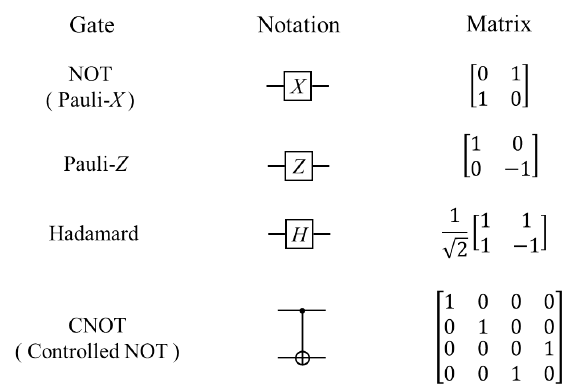
$|0\rangle=$

$|1\rangle=$

Adiabatic Quantum Computing

$H(t) =\frac{1-t}{\tau} \:H_{\rm mix} + \frac{t}{\tau}\: H_c$

Slow evolution during time $\tau$

Quantum Adiabatic Theorem: A quantum system that starts in the ground state of a time-dependent Hamiltonian, remains in the in the instantaneous ground state provided the Hamiltonian changes sufficiently slowly.

Z|0\rangle = |0\rangle

Z|1\rangle = -|1\rangle

EVOLutıon of a CLOSED quantum system

$|\psi\rangle' = U |\psi\rangle$

State of the system at $t_1$

State of the system at $t_2$

Unitary operator

i h \frac{d |\psi\rangle}{dt}|\psi\rangle = H |\psi\rangle

Hermitian operator

Hamiltonian

H = \sum e |E \rangle \langle E|

Eigenstate

Energy

Lowest energy state: Ground state

|\psi(t)\rangle = exp(-itH) |\psi(0)\rangle

Unitary

Isıng model

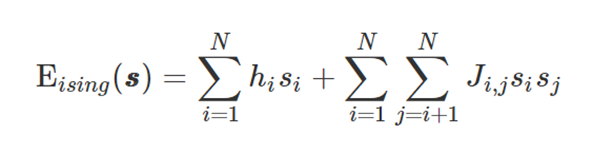
Consider Hamiltonian

\displaystyle \mathcal{H}_I = \sum_{i\in V} h_i Z_i + \sum_{(i,j)\in E} J_{ij} Z_iZ_j

Z|0\rangle = |0\rangle = (-1)^0 |0\rangle

Z|1\rangle = -|1\rangle = (-1)^1 |0\rangle

Note that

\displaystyle \mathcal{H}_I |\phi \rangle = \left (\sum_{i\in V} h_i Z_i + \sum_{(i,j)\in E} J_{ij} Z_iZ_j \right ) |\phi \rangle

\displaystyle \mathcal{E}_I = \sum_{i\in V} h_i (-1)^{\phi_i} + \sum_{(i,j)\in E} J_{ij} (-1)^{\phi_i}(-1)^{\phi_j}

Yields energy function

Hence,

Corresponds to

$s_i \in \{-1,1\} $

where,

Example - MAx-cut Problem

$\displaystyle \sum_{(i,j) \in E} Z_iZ_j $ = $Z_0Z_1 + Z_1Z_2 + Z_2Z_3 + Z_0Z_3$

Corresponding Hamiltonian:

$\min.~ \displaystyle \frac{1}{2}\sum_{(i,j) \in E} (s_is_j-1)$

$\implies \min. \displaystyle \sum_{(i,j) \in E} s_is_j $

\max. \displaystyle \frac{1}{2}\sum_{(i,j)\in E} 1-s_is_j =

U(H_P,\gamma) = e^{-i\gamma H_P} = e^{-i\gamma Z_0Z_1}e^{-i\gamma Z_1Z_2} e^{-i\gamma Z_2Z_3} e^{-i\gamma Z_0Z_3}

Quantum Approximate Optimization Algorithm (QAOA)

For the gate based model

$\gamma_i$ and $\beta_i$ optimized by external classical procedure

$$|\gamma,\beta\rangle = \prod_{i=1}^p \exp(-\mathrm{i} \beta_iH_{\rm mix})\exp(-\mathrm{i} \gamma_iH_c) |+\rangle^{\otimes n}$$

Can be viewed as a trotterization of AQC

Zhou, Leo, et al. "Quantum approximate optimization algorithm: Performance, mechanism, and implementation on near-term devices." Physical Review X 10.2 (2020): 021067.

$H(t) =\frac{1-t}{\tau} \:H_{\rm mix} + \frac{t}{\tau}\: H_c$

|\psi(t)\rangle = exp(-itH) |\psi(0)\rangle

How to implement QAOA?

Hamiltonian:

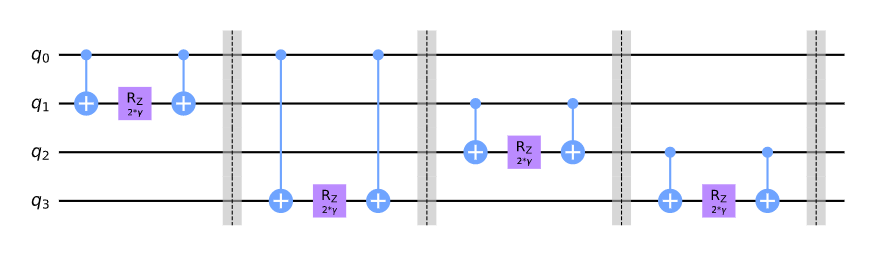
https://qiskit.org/textbook/ch-applications/qaoa.html

H_P = Z_0Z_1 + Z_1Z_2 + Z_2Z_3 + Z_0Z_3

exp(-iZ\otimes Z t) =

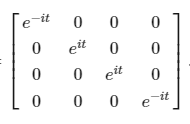
Unitary:

U(H_P,\gamma) = e^{-i\gamma H_P} = e^{-i\gamma Z_0Z_1}e^{-i\gamma Z_1Z_2} e^{-i\gamma Z_2Z_3} e^{-i\gamma Z_0Z_3}

Node $\leftrightarrow$ Qubit

Edge $\leftrightarrow$ Interaction (Gate)

Universalıty of qaoa

Morales, M.E., Biamonte, J.D. and Zimborás, Z., 2020. On the universality of the quantum approximate optimization algorithm. Quantum Information Processing, 19(9), pp.1-26.

= U(H_X, \beta_p)U(H_Z, \gamma_p)\cdots U(H_X, \beta_1)U(H_Z, \gamma_1)|+\rangle^{\otimes n}

|\gamma,\beta\rangle = \prod_{i=1}^p \exp(-\mathrm{i} \beta_iH_{\rm X})\exp(-\mathrm{i} \gamma_iH_Z) |+\rangle^{\otimes n}

Universality in general: Possibility of generating arbitrary unitary operations by composition of elementary gates in a gate set.

Back to QAOA

For fixed $ H_X$ and $H_P$ and $p\in \mathbb{Z}$, the family of circuits defined by QAOA corresponds to the set of unitaries

\mathcal{C}_{H_Z,H_X}^p = \{U(H_X, \beta_p)U(H_Z, \gamma_p)\cdots U(H_X, \beta_1)U(H_Z, \gamma_1)|+\rangle^{\otimes n}~|~ \gamma_j, \beta_j \in \mathbb{R}\}

\mathcal{C}_{H_Z,H_X} = \bigcup_p \mathcal{C}_{H_Z,H_X}^p

Universalıty of qaoa

Morales, M.E., Biamonte, J.D. and Zimborás, Z., 2020. On the universality of the quantum approximate optimization algorithm. Quantum Information Processing, 19(9), pp.1-26.

For fixed $ H_X$ and $H_P$ and $p\in \mathbb{Z}$, the family of circuits defined by QAOA corresponds to the set of unitaries

\mathcal{C}_{H_Z,H_X}^p = \{U(H_X, \beta_p)U(H_Z, \gamma_p)\cdots U(H_X, \beta_1)U(H_Z, \gamma_1)|+\rangle^{\otimes n}~|~ \gamma_j, \beta_j \in \mathbb{R}\}

\mathcal{C}_{H_Z,H_X} = \bigcup_p \mathcal{C}_{H_Z,H_X}^p

For fixed $H_Z$ and $H_X$ acting on $n$ qubits, we say QAOA is universal if any element in the full unitary group $U(2^n)$ is approximated to arbitrary precision (up to a phase) by an element of $\mathcal{C}_{H_Z,H_X}$.

Question: For which $H_Z$, $\mathcal{C}_{H_Z,H_X}$ is universal?

A Lie algebra is a vector space $g$ over some field $F$ together with a binary operation

$[~,~]: g\times g \rightarrow g$ satisfying some relationships.

LIE ALGEBRA

Ex: $[x,y]=-[y,x]$

Given a set of Hamiltonians $P = \{i H_1,i H_2,\dots,i H_q \}$, we call the smallest real Lie algebra $\mathcal L$ containing the elements of $P$ the generated Lie algebra of $P$.

We will denote the generated Lie algebra as

\mathcal{L}= \langle P \rangle_{Lie} = \langle\{i H_1,i H_2,\dots,i H_q \}\rangle_{Lie}.

e^\mathcal{L}=\{e^{A_1}, e^{A_2}\cdots e^{A_m}: m\in \mathbb{N}, A_j \in \mathcal{L} \}

is the set of reachable unitaries.

In QAOA setting, we are interested in knowing whether the Lie algebra generates (up to a phase) the entire unitary group $U(2^n)$.

\mathcal{L}=\langle i H_Z ,i H_X \rangle_{Lie}

commutators and operators

$[X_i, Y_i] = 2iZ_i$

$[Y_i, Z_i] = 2iX_i$

$[Z_i, X_i] = 2iY_i$

$[A,B] = AB-BA$

$A_iB_j = B_jA_i$ for $A,B \in \{X,Y,Z\}$ and $i \neq j$

\mathcal{L}=\langle i H_Z ,i H_X \rangle_{Lie}

Show that $e^\mathcal{L}$ contains universal gates, such as any 1-qubit gate and CNOT

MAIN STRATEGY

Example:

If $X_j \in \mathcal{L} $ for all $j$, then the gate $R_X(\theta) \in e^{\mathcal{L}}$
If $Z_{i}Z_j \in \mathcal{L}$ for all $(i,j) \in E$, then CNOT gate $\in e^{\mathcal{L}}$

Zero Forcıng SET

Given a simple graph $G = (V, E)$, let $S\subseteq V$ be an initial set of "infected" vertices which are colored red and suppose that the remaining "non-infected" vertices are colored black.

Consider an iterative process, where at each step, the color of a black vertex changes into red if it is the only black neighbor of a red vertex.

$S$ is called a zero forcing set if starting with the vertices in $S$, all the vertices are colored in red at the end of this process i.e. all vertices are infected.

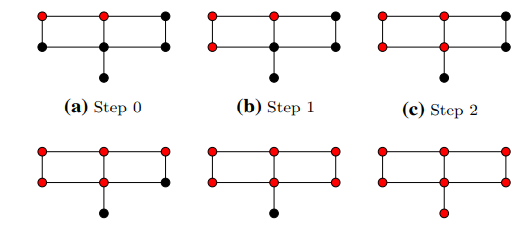
Zero forcing process

Universalıty of qaoa defined on graphs

Consider simple graph $G=(V,E)$ and $S\subseteq V$.

Let

\displaystyle H_Z = \gamma \sum_{(i,j)\in E} Z_iZ_j + \sum_{i \in S} \omega_i Z_i + \omega \sum_{i \in V \setminus S} Z_i

\displaystyle =\gamma H_{\gamma} + \sum_{i \in S} \omega_i Z_i + \omega H_V

\displaystyle H_X = \sum_{i\in V} X_i

Theorem Let $G=(V,E)$ be a simple graph and $S \subseteq V$. Consider $S$ as the initial set of infected nodes in a zero forcing process. Let $\gamma,\omega,\omega_i$ be rationally independent. If $S$ is a zero forcing set, then $Z_kZ_j\in \langle H_Z,H_X\rangle_{Lie}$ for all $ (k,j) \in E$ and $X_k\in \langle H_Z,H_X\rangle_{Lie}$ for all $k\in V$.

Universalıty of qaoa defined on graphs

H_Z = Z_0Z_1 + Z_1Z_2 + Z_2Z_3 + Z_0Z_3 + \sqrt{2} Z_0 + \sqrt{3} Z_3 + \sqrt{5}Z_1 + \sqrt{5}Z_2

\displaystyle H_Z = \gamma \sum_{(i,j)\in E} Z_iZ_j + \sum_{i \in S} \omega_i Z_i + \omega \sum_{i \in V \setminus S} Z_i

$S=\{0,3\}$. $S$ is z zero-forcing set.

QAOA defined by $H_Z$ is universal.

H_Z = 2Z_0Z_1 + 3Z_1Z_2 + Z_0Z_2 + \sqrt{2}Z_1 + \sqrt{3} Z_2 + \sqrt{3} Z_3

Universalıty of qaoa defined on graphs

\displaystyle H_Z = \gamma \sum_{(i,j)\in E} Z_iZ_j + \sum_{i \in S} \omega_i Z_i + \omega \sum_{i \in V \setminus S} Z_i

No common $\gamma$

H_Z = 2Z_0Z_1 + 2Z_1Z_2 + 2Z_0Z_2 + \sqrt{2}Z_1 + \sqrt{3} Z_2 + \sqrt{3} Z_3

$S=\{1\}$ Not a zero forcing set

Theorem does not apply

Proof Idea:

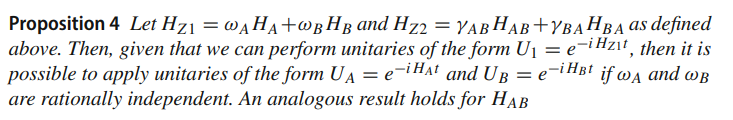
Since $\gamma,\omega,\omega_i $ are rationally independent, we can generate $H_\gamma, H_V, Z_i$ for $i\in S$.
If we can generate $Z_i$, we can also generate $X_i$ for $i \in S$. (Since we also have $H_X$).

$X_i,i \in S$

\displaystyle H_Z = \gamma \sum_{(i,j)\in E} Z_iZ_j + \sum_{i \in S} \omega_i Z_i + \omega \sum_{i \in V \setminus S} Z_i

\displaystyle H_X = \sum_{i\in V} X_i

\displaystyle =\gamma H_{\gamma} + \sum_{i \in S} \omega_i Z_i + \omega H_V

Proof Idea:

\displaystyle H_Z = \gamma \sum_{(i,j)\in E} Z_iZ_j + \sum_{i \in S} \omega_i Z_i + \omega \sum_{i \in V \setminus S} Z_i

\displaystyle H_X = \sum_{i\in V} X_i

\displaystyle =\gamma H_{\gamma} + \sum_{i \in S} \omega_i Z_i + \omega H_V

Let $i,j\in S $ be neighboring vertices in $G$.
Consider the commutator:

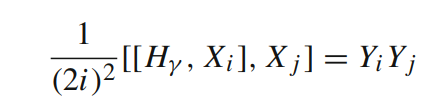
Hence, we can also generate $Z_iZ_j $.

$X_i,i \in S$

$Z_iZ_j, i,j \in S$

Proof Idea:

\displaystyle H_Z = \gamma \sum_{(i,j)\in E} Z_iZ_j + \sum_{i \in S} \omega_i Z_i + \omega \sum_{i \in V \setminus S} Z_i

\displaystyle H_X = \sum_{i\in V} X_i

\displaystyle =\gamma H_{\gamma} + \sum_{i \in S} \omega_i Z_i + \omega H_V

Consider now $i\in S $ that has only one non-infected neighbor $j \in V \setminus S$.
Define $H_i$ as $H_\gamma$ with the interaction terms corresponding to infected neighbors of $i$ subtracted.
Consider the commutator

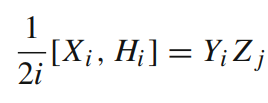
$X_i,i \in S$

$Z_iZ_j, i,j \in S$

Thus, $Z_iZ_j$ can be generated. Then, commute with $H_X − X_i$ and generate $Z_iY_j$ which commuted with $Z_iZ_j$ generates $X_j$.

$X_j, j$ is the only non-infected neighbor of $i$

$Z_iZ_j, i \in S$ $j$ is the only non-infected neighbor of $i$

Proof Idea:

\displaystyle H_Z = \gamma \sum_{(i,j)\in E} Z_iZ_j + \sum_{i \in S} \omega_i Z_i + \omega \sum_{i \in V \setminus S} Z_i

\displaystyle H_X = \sum_{i\in V} X_i

\displaystyle =\gamma H_{\gamma} + \sum_{i \in S} \omega_i Z_i + \omega H_V

$X_i,i \in V$

$Z_iZ_j, (i,j) \in E$

This is analogous to an infection step in the zero forcing process.
It is then easily seen that if $S$ is zero forcing, then all one-qubit and two-qubit operators are generated in the graph

GENERALIZATON

Consider simple graph $G=(V,E)$ and $S\subseteq V$. Partition the set of edges $E$ into $q$ disjoint sets $\{E_i\}_{i\in[q]}$ such that $\bigcup_{i\in[q]} E_i = E.$

\displaystyle H_Z = \sum_{k=1}^q \sum_{(i,j)\in E_k} \gamma_k Z_iZ_j + \sum_{i \in S} \omega_i Z_i + \omega \sum_{i \in V \setminus S} Z_i

\displaystyle =\sum_{k=1}^q \gamma_k H_{\gamma_k} + \sum_{i \in S} \omega_i Z_i + \omega H_V

\displaystyle H_X = \sum_{i\in V} X_i

Same result applies if $S$ is a generalized zero-forcing set.

The generalized zero forcing process proceeds by considering each infected vertex and the subgraph $G_1 = (V, E_1)$.

If an infected vertex has a single non-infected neighbor in $G_1$, then infect this new vertex and add it to $S$.
Then, proceed in the same fashion with the neighbours of vertices of $S$ in graphs $G_2, G_3,\dots, G_q$ .

UNIVERSALITY WITHOUT ZERO FORCING

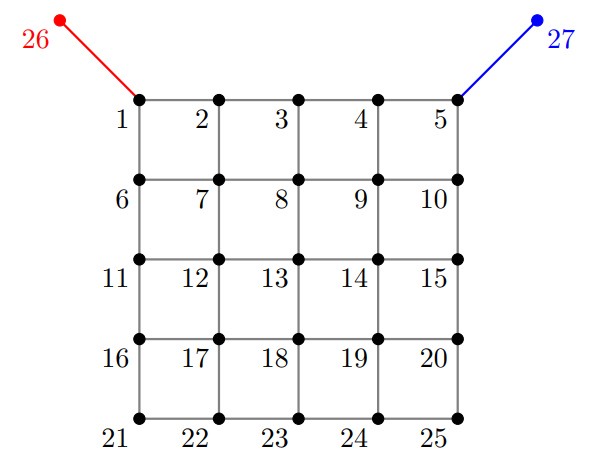
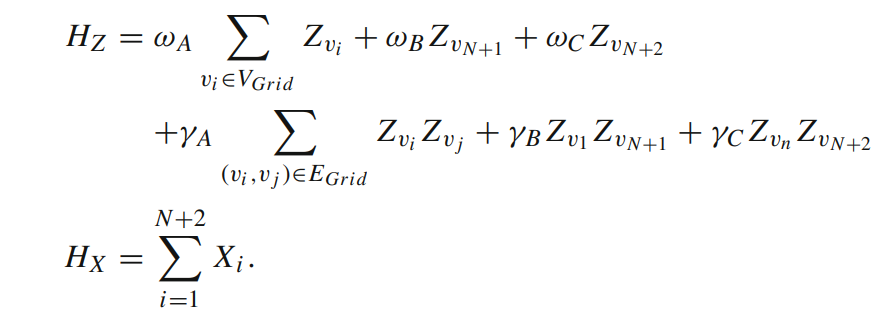
$N=25$

HYPERGRAPHS

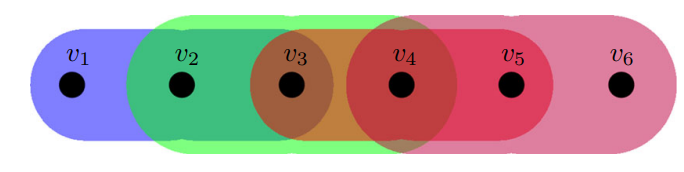
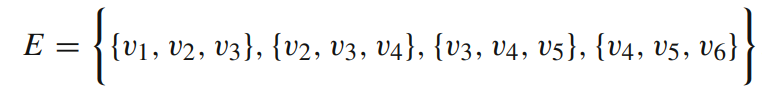
Consider a hypergraph $\mathcal{G} = (V, E)$ where $|e| \leq 3$ for all $e \in E$; a hyperzero forcing process on $G $ consists of an initial set of vertices $S_1 \subseteq V$ and an initial set of 2-edges $S_2$ which we will consider as “infected”.

At each step, a pair of infected vertices $v_1, v_2$ infects a non-infected 3-neighbour $w$ if $w$ is the only non-infected 3-neighbour of $v_1$ and $v_2$ and also the 2-edge $v_1, v_2$ is infected.

We call $S_1$ and $S_2$ hyper-zero forcing sets if we can infect all the graphs by starting with $S_1$ and $S_2$ infected.

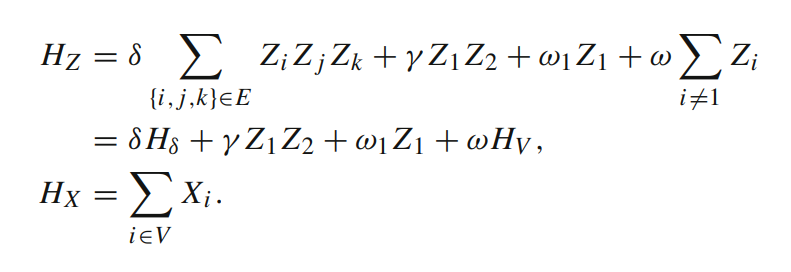
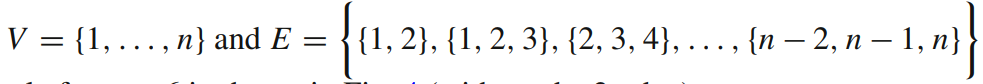
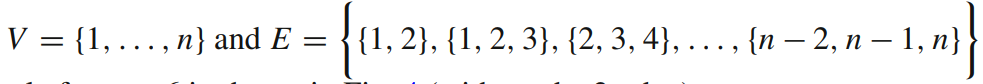
OPEN QUESTIONS

Can we define a more general graph process than zero-forcing for universality?

For Hamiltonians involving higher order terms, can we find other classes of Hamiltonians and show universality through hyperzero forcing process?