long chains
Parker Rule
MGGG
April 22, 2020
motivation
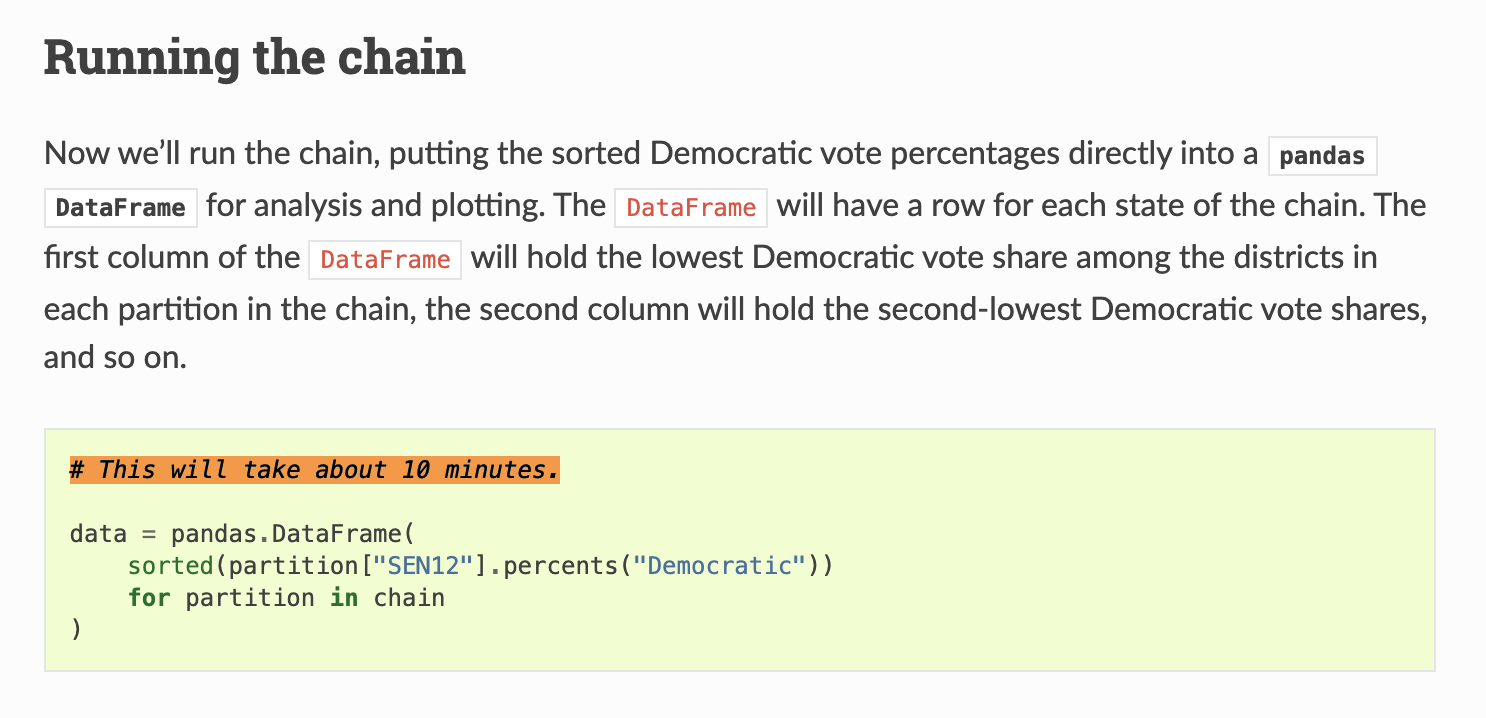
GerryChain is slow...
Why?
motivation

ouch! 😬
For a typical ReCom run on Pennsylvania, random spanning tree operations take up ~70% of runtime.
motivation

...and calls to a single NetworkX function take ~40% of runtime!
motivation

This is not particularly surprising.
DeFord et al. 2020
motivation
~50x slowdown relative to graph-tool 😢
...but NetworkX is superior in other ways (API, documentation, ease of installation, popularity).
AmDAHl's LAW
(say, by 50x!)
xkcd
AmDAHl's LAW
What if we could make the slow bit faster? 🤔
(say, by 50x!)
AmDAHl's LAW
Speeding up just the biggest NetworkX call...
AmDAHl's LAW
Speeding up all of random_spanning_tree()...
AmDAHl's LAW
Very optimistically...
AmDAHl's LAW

This stuff also matters!
AmDAHl's LAW
Abandoning this branch was probably wise.
AmDAHl's LAW
Solution: make all the parts faster.
sites.tufts.edu/vrdi

Use a compiled language!
what about FLIP? 🙂🙃
Less computation per step...
but usually more steps.
Pennsylvania flip-to-ReCom ratio: ~100x
1k ReCom steps in ~10 minutes
100k flip steps in ~10 minutes
what about FLIP?
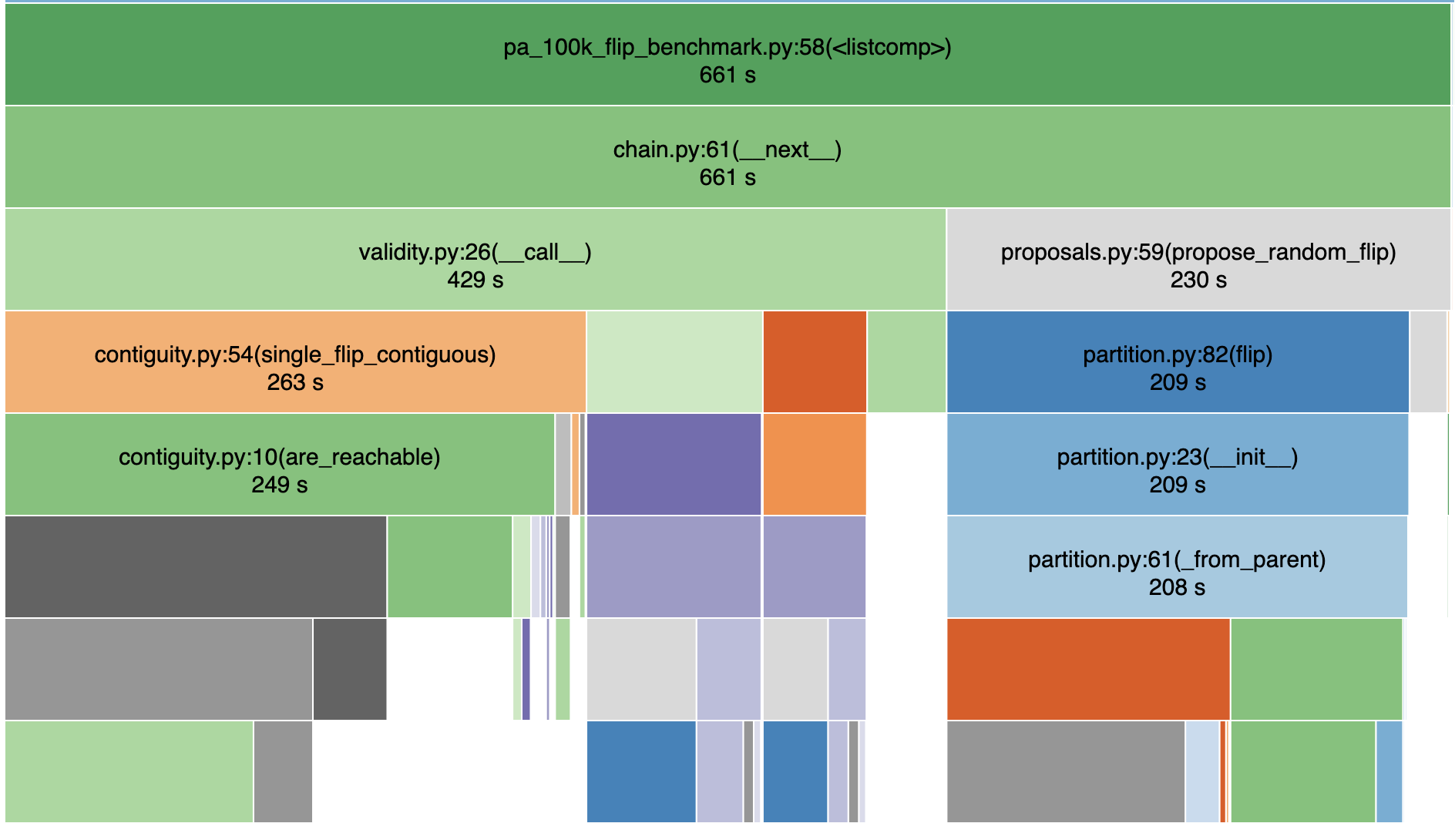
Contiguity checks are the slow bit this time.
(depth-first search at each step)
what about FLIP?

Contiguity checks are the a slow bit this time.
Creating new partitions also takes much of the runtime!
what's in a gerrychain partition?

Each new partition of Pennsylvania costs ~20KB
(with optimizations!)
github.com/mggg/GerryChain
what's in a gerrychain partition?
1 million Pennsylvania flip steps (easily computable in two hours) costs ~20GB of RAM to store.
Even with operating system RAM compression, large ensembles (millions of plans) are extremely challenging to work with!
solving the memory problem
Solution 1: compute statistics on the fly rather than saving every plan and computing statistics ex post facto.
Pros:
Trivial to implement
Potential O(1) memory usage (for pre-binned histograms, etc.)
Cons:
Loss of flexibility
(what if you don't know what statistics you want?)
solving the memory problem
Solution 2: save the deltas between each step, plus the occasional snapshot of the full plan for fast reconstruction.
Pros:
Entire chain preserved—more flexibility
Cons:
More complicated to implement
Doesn't work well for ReCom (naïvely)
Doesn't scale well to billions of steps
solving the memory problem
The answer probably depends on scale.
Thousands of plans — save everything
Millions of plans — use a more compact representation; save statistics
Billions of plans — save (rich) statistics only
Trillions of plans — save summary statistics
GerryChain theoretically supports all of these scales, but it is oriented around working with thousands of plans.
Why work with Long chains, anyway?
Optimization
Richer ensembles
Developing new chains
High coverage (small grid experiments)
Rewriting flip and recom
GerryChain is a fantastic preprocessing and analysis tool. Why throw that out?
Load and filter geodata
Define chain
Run chain
🕐🕓🕖
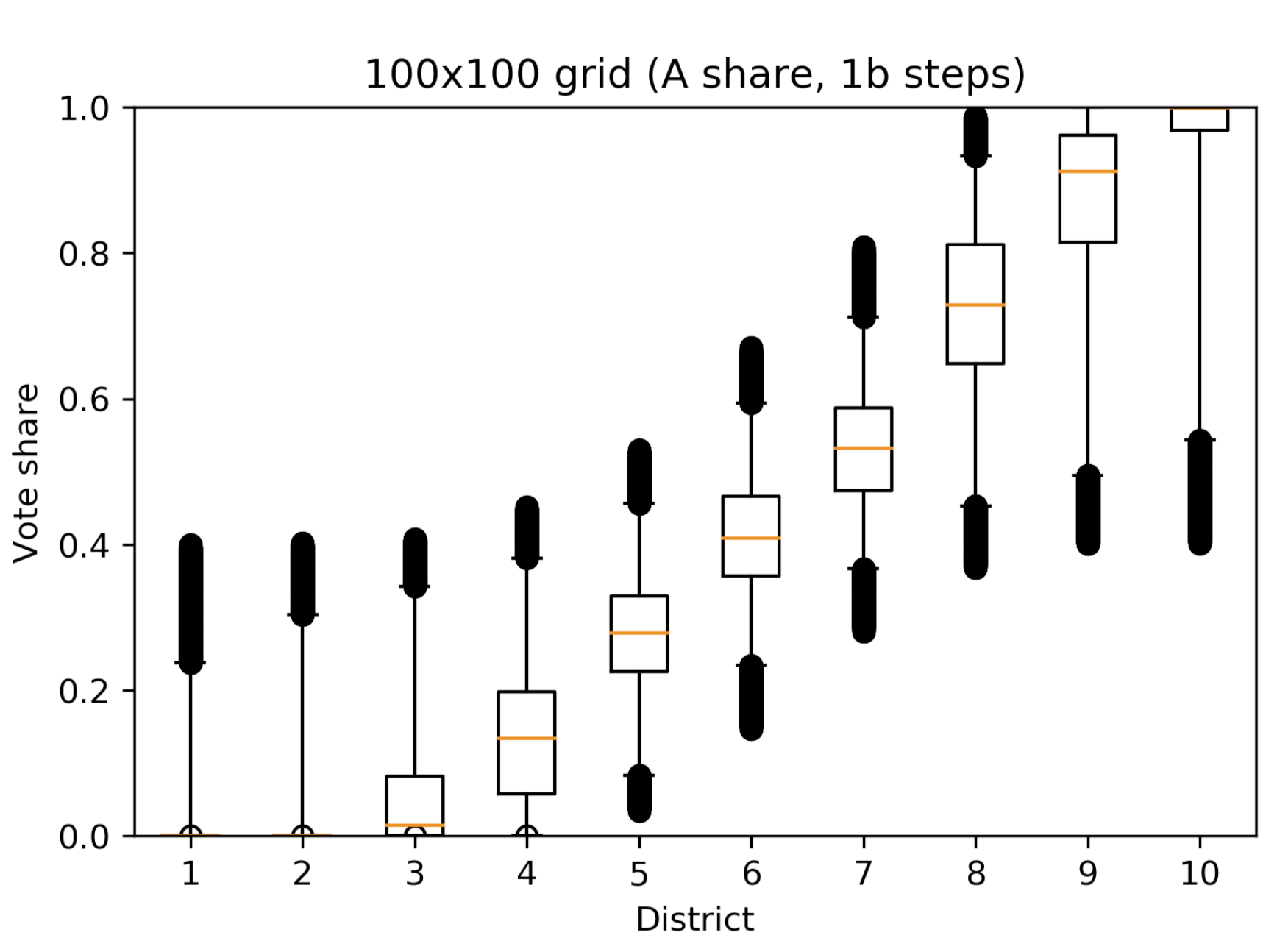
Make a nice boxplot
Rewriting flip and recom
GerryChain is a fantastic preprocessing and analysis tool. Why throw that out?
Load and filter geodata
Define chain
Load chain results
Make a nice boxplot
Run optimized chain
🔥
INSPO!
Counting polyomino tilings (districts on a grid)
mggg.org/table
inspo!

Zach Schutzman's polyomino tiling enumeration code
github.com/zschutzman/enumerator
Rewriting flip and recom


Rewriting flip and recom
| Julia? | C++? |
|---|---|
| Optimized for scientific computing (built-in linear algebra, graph analysis, and tabular data libraries) | More mature and well-known |
| Python-like syntax (+ REPL!) | Easier to use with Python |
Dependencies are annoying, particularly in the C++ context.
Most people at MGGG (including myself) primarily use Python, and Julia is easier to learn with a Python background.
new tools
first generation: flips.jl
Originally written to compute ~1-billion-step flip chains for the ReCom paper (DeFord, Duchin, Solomon 2019)
Supports basic on-the-fly computation of statistics
first generation: flips.jl
first generation: flips.jl
A quick benchmark...
100k Pennsylvania flip steps
(2% population tolerance, no compactness constraint, no statistics)
GerryChain: 22 min, 34 sec
Flips.jl: 13.6 sec
~100x speedup!
Second generation: flips.jl (recom edition)
Originally written to compute ~10-million-step chains for the reversible ReCom paper (Cannon, Duchin, Randall, Rule; forthcoming)
Integrated with GerryChain via Python-Julia bindings
Second generation: flips.jl (recom edition)
Another benchmark...
1k Pennsylvania ReCom steps
(2% population tolerance, no compactness constraint, no statistics)
GerryChain: 6 min, 33 sec
Flips.jl: 14.1 sec
~28x speedup!
python-julia bindings
Goal: use GerryChain for preprocessing and analysis.
Calling Julia from Python is finicky, so it best to minimize interaction. (This also cuts down on overhead!)
Strategy: Loose coupling (JSON serialization)
python-julia bindings

Extremely simple (~30 lines)
takes in an initial partition; returns a block of partitions
python-julia bindings
Converting the output of the Julia chain into GerryChain partitions is effective up to the memory bottleneck.
If we save only a few partitions and record statistics, this strategy works well for up to ~100m Pennsylvania ReCom steps on the HPC cluster.
Computing statistics and initializing GerryChain partitions is the CPU bottleneck; this can be largely alleviated through parallelization.
parallelizing chains
Markov chains are inherently serial—the next step depends on the last step.
However, proposals starting from the same step can be parallelized. This can result in large wall-clock speedups for chains with low acceptance probabilities (roughly proportional to the number of cores used).
Third generation: Gerrychain.jl
Coming soon!
(see github.com/mggg/GerryChainJulia)
Collaboration between me and Bhushan Suwal
Pure Julia—removing Python entirely should allow for faster, longer chains (but can still be called from Python if desired)
Parallelization support
Built-in support for many common statistics and analyses
May still depend on/integrate with Python geodata tools for preprocessing
Third generation: Gerrychain.jl
Coming soon!
(see github.com/mggg/GerryChainJulia)
Please be our beta testers!
epilogue: Cluster computing with julia
Julia has rich support for cluster computing and integrates with the Slurm job manager on the Tufts HPC cluster with just a few lines of code.
Account limit: ~450 cores 🤯
Could be used for large-scale optimization experiments
case study: optimalvotes.jl
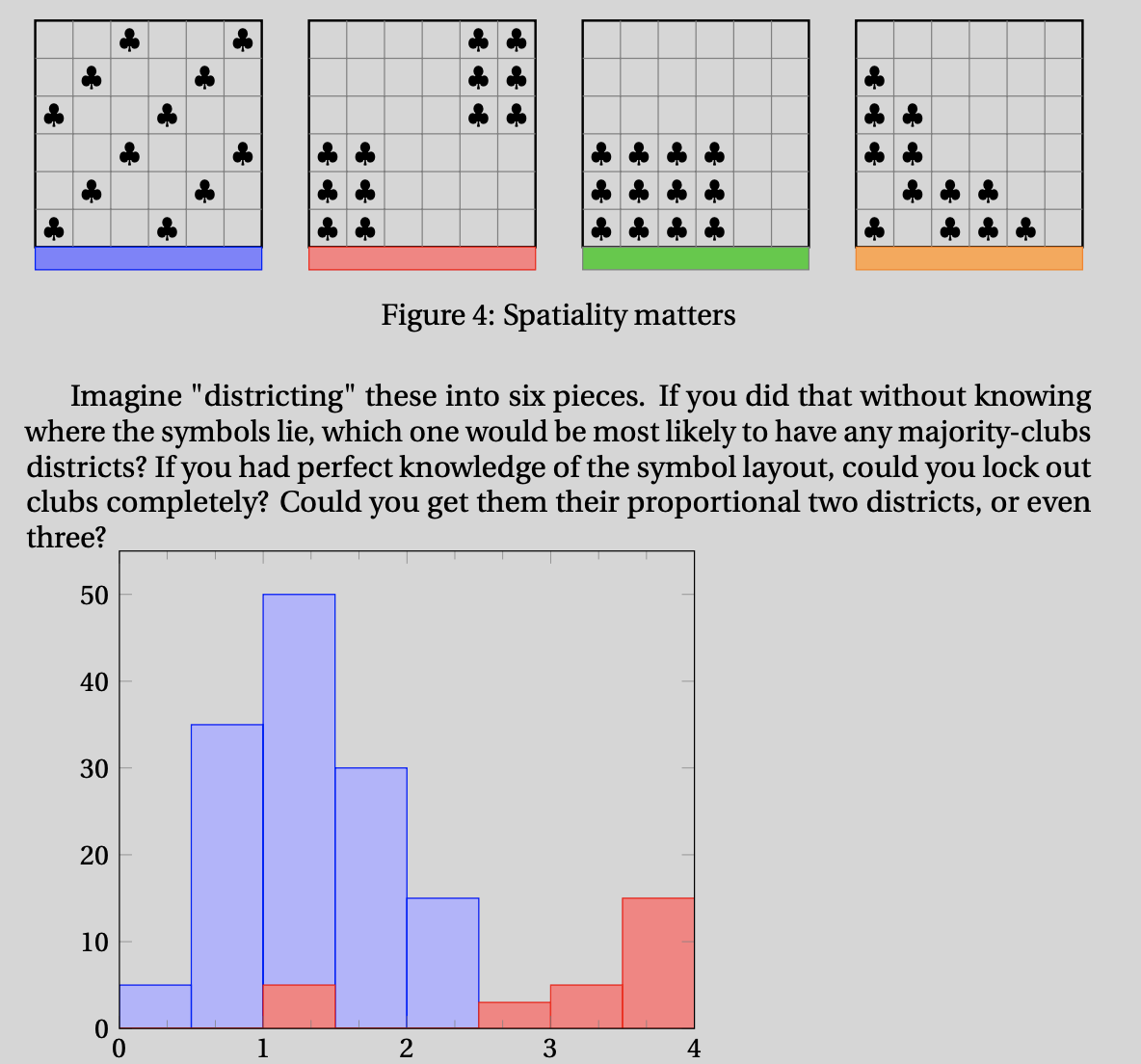
Question: How do vote patterns map to seat shares?
Hypothesis: Spatiality matters.
(Diffuse patterns and overly packed patterns perform worse.)
from preprint of Political Geometry
case study: optimalvotes.jl
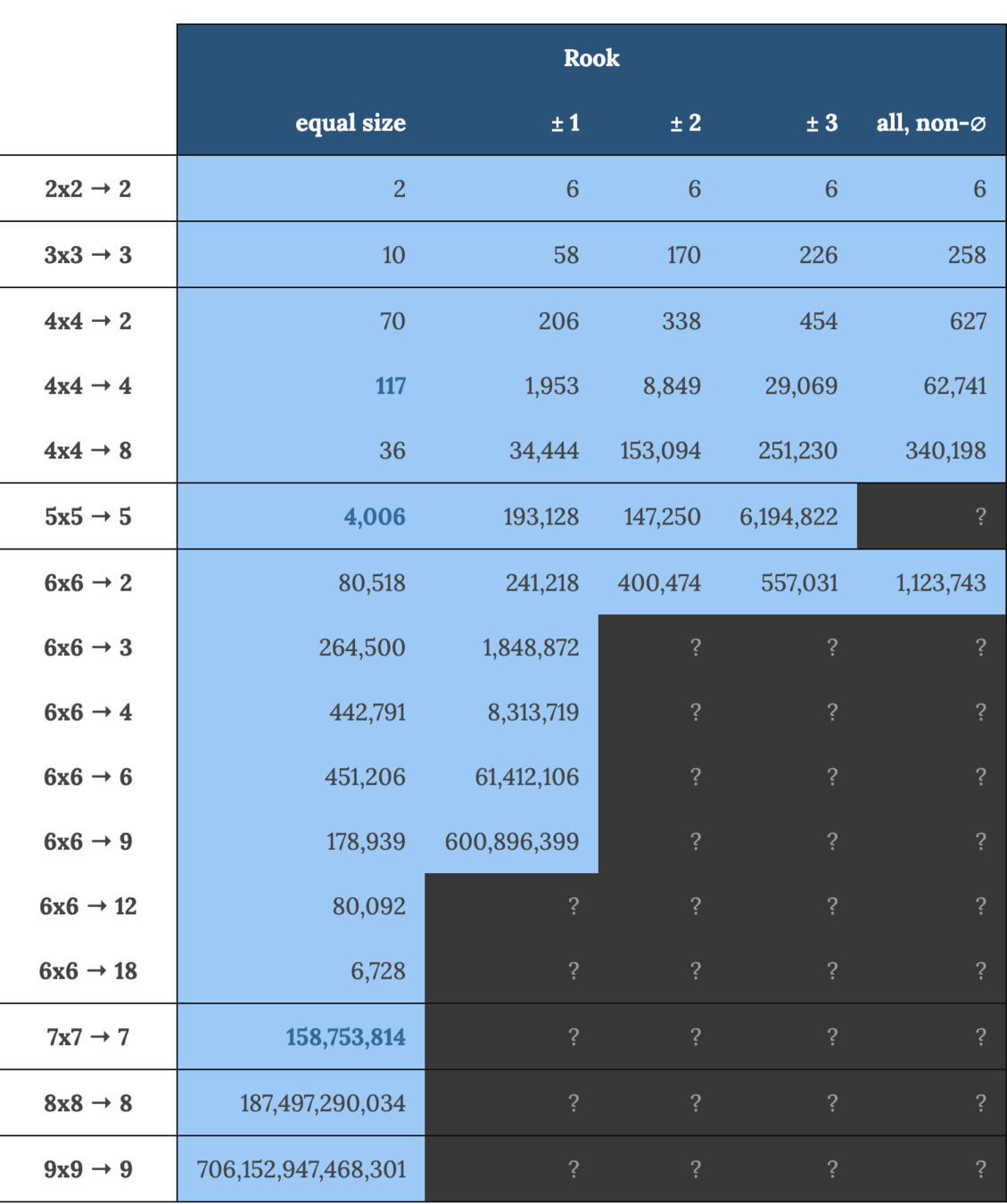
Goal (6x6 grid → 6 districts, 12 club voters):
evaluate 1,251,677,700 vote distributions over 451,206 districtings
What is the best vote distribution for clubs over all districtings?
What is the worst?
First-past-the-post voting introduces nonlinearities that make this problem hard.
case study: optimalvotes.jl
Approach:
Decompose ~450,000 districtings into ~2,500 polyominoes
Remove vote distributions that are redundant by symmetry
Compute all polyomino-vote distribution pairings to find best and worst expected seat shares
Solved in ~3 hours over hundreds of cores using Distributed.jl!