Low-dimensional linear programming
Reminder: what is linear programming?
Most generically, a linear program is a problem of the form
(n variables, m constraints)
Reminder: what is linear programming?
(Sometimes, we add another constraint.)
How are linear programs solved?
Simplex method (Dantzig, 1940s)
Basic idea: pivot around on the convex polytope of constraints
From User:Sdo (Wikimedia). CC BY-SA 3.0.
Works well in practice, but technically has exponential asymptotic complexity (Klee 1973)
How are linear programs solved?
Karmarkar's algorithm (1984)
Runs in polynomial time...
Complicated (relies on projective geometry)
Constraints on a plane
Two types (ignoring vertical constraints):
Constraints on a plane
Some constraints may be redundant.
Constraints on a plane
Ultimately, we are interested in the intersection of half-planes.
How many vertices can we have?
Counting vertices
By McMullen's upper-bound theorem, there are only O(n) vertices to consider for the intersection of half-spaces in and .
Counting vertices
In general, a convex hull of dimension d has facets, and a polytope with n facets can have vertices.
Thus, the (asymptotically) best methods for low-dimensional linear programming depend on dimension.
Half-plane intersection
Naive algorithm
Let the set of constraints be P. For every unique
, compute the intersection and check to see if the vertex satisfies all constraints.
Runtime: O(n³)
Half-plane intersection
Divide-and-conquer (Shamos 1978)
Recursively merge half-planes until reaching a (potentially unbounded) convex hull.
D&C half-plane intersection
Need to deal with unboundedness (...but each chain can only have two rays)
D&C half-plane intersection
Runtime (Shamos 1978): O(n log n) — reduces to sorting
Can we do better?
Half-plane intersection
Duality — map constraints in the primal to points in the dual and take the convex hull; edges are intersections.
Requires taking the convex hull—O(n log n)
Incremental — merge in one half-plane at a time.
Still O(n²) or O(n log n) — where to merge?
Pruning (Megiddo 1983)
What if taking all the half-plane intersections is overkill?
Rewrite the LP.
Pruning (Megiddo 1983)
What if taking all the half-plane intersections is overkill?
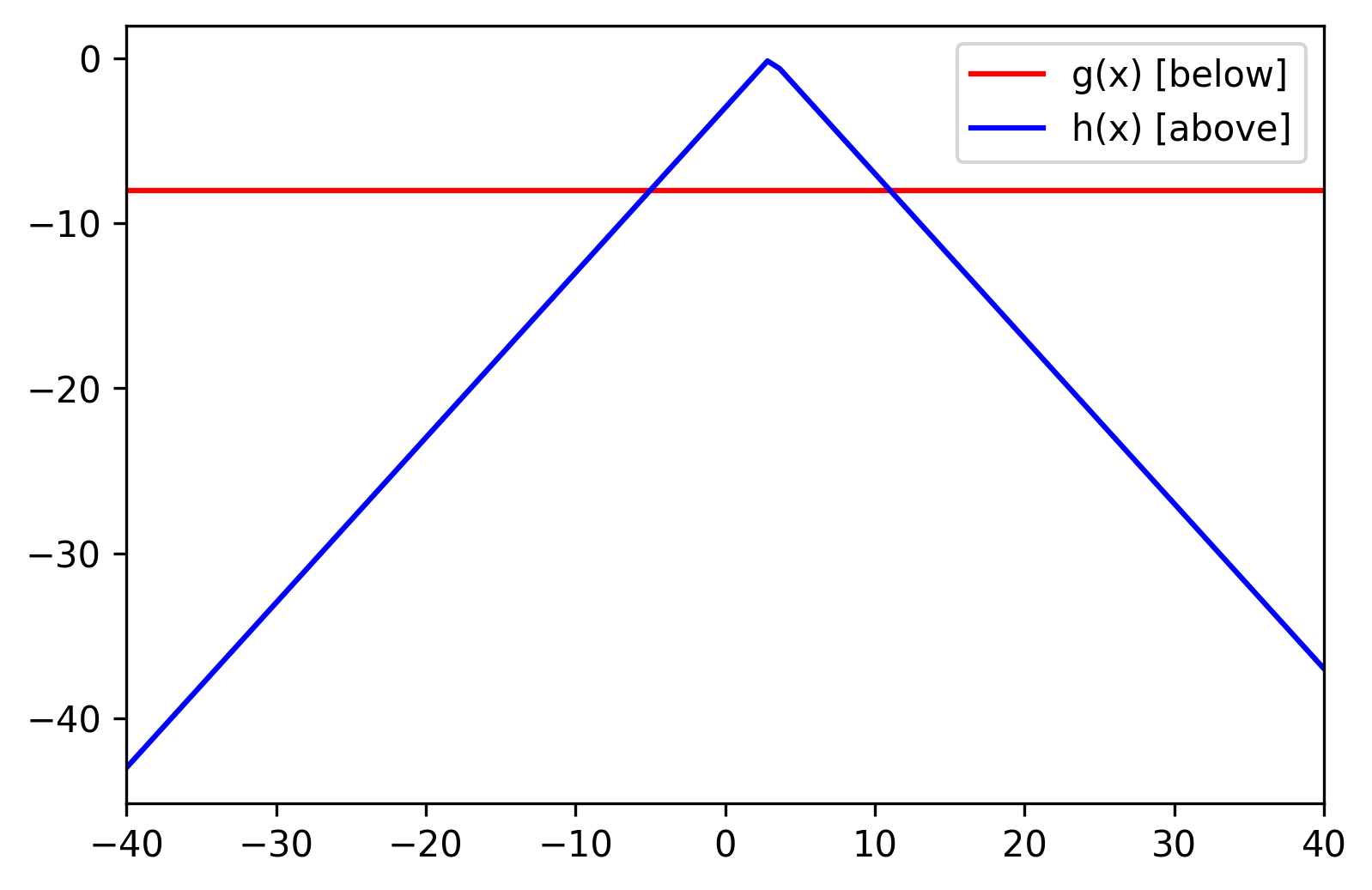
Now we're just looking for the x* that induces the minimum y-value.
Observation: every x has a tightest upper and lower constraint.
Pruning (Megiddo 1983)
What if taking all the half-plane intersections is overkill?
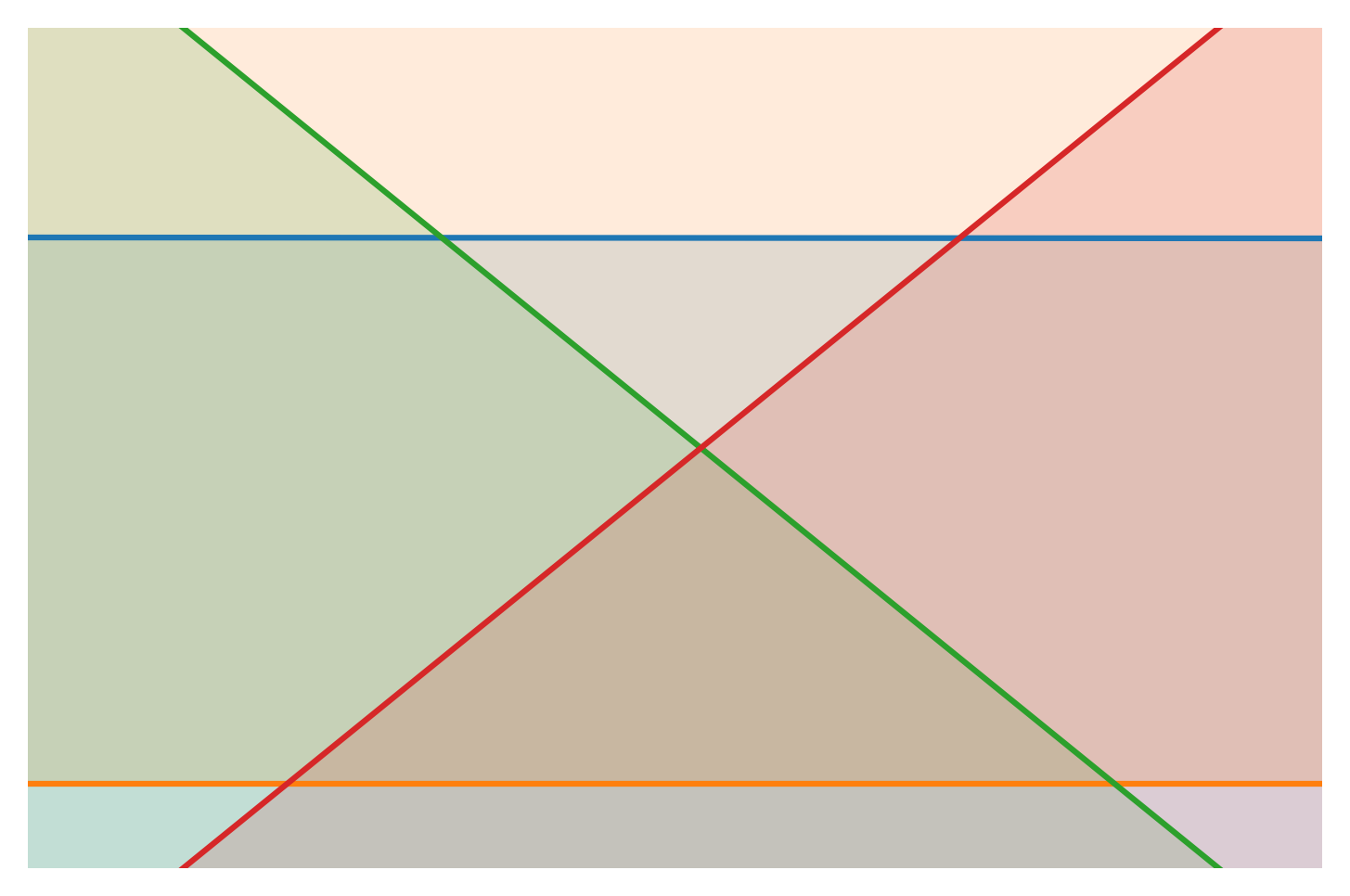
Merge constraints piecewise.
Eliminating constraints
Our goal is to narrow down the range of x-values. First we must find a feasible range; then we must find x* (or determine that the problem is infeasible).
We move along edges of the piecewise constraints and attempt narrow down the range of x-values. The more we narrow down the range, the more constraints we can eliminate.
The algorithm removes approximately n/4 points at each step, yielding an O(n) runtime.
The Megiddo paradigm
Megiddo 1983 solves several related problems in O(n), including the smallest enclosing circle problem. Shamos offers a O(n log n) algorithm for this problem (naively O(n⁴)) using farthest-point Voronoi diagrams.
