Multi-splay trees and tango trees
Christian Altamirano
Parker Rule
May 19, 2021
Dynamic optimality
Recall: it is conjectured that splay trees are dynamically optimal (Sleator and Tarjan 1985). However, this conjecture remains unproven.
Consider a static universe of keys. Every access sequence X has an optimal BST that requires OPT(X) unit cost operations.
A BST data structure is dynamically optimal if every sequence X requires O(OPT(X)) operations.
O(log log n)-competitive BSTs
Tango trees (Demaine et al. 2005): preferred paths of length O(log n) are represented as red-black trees in a tree of trees.
Multi-splay trees (Wang, Derryberry, and Sleator 2006): Somewhat similar to tango trees, but preferred paths are represented as splay trees instead. Better (amortized) worst-case performance.
Multi-splay trees
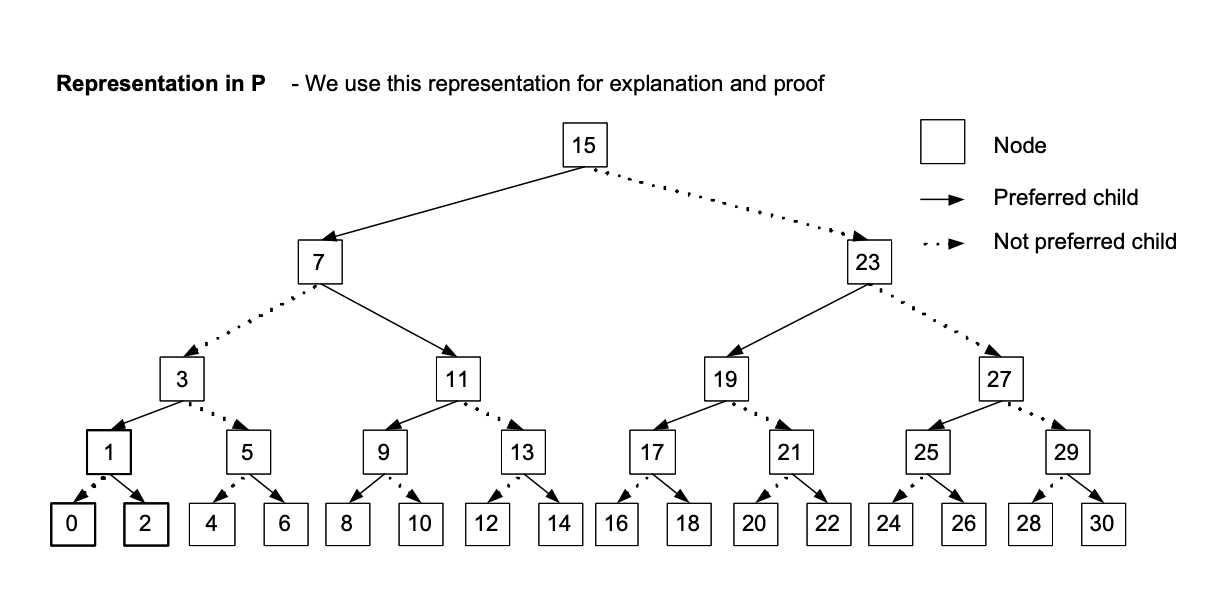
Source: Sleator and Wang 2004
Multi-splay trees
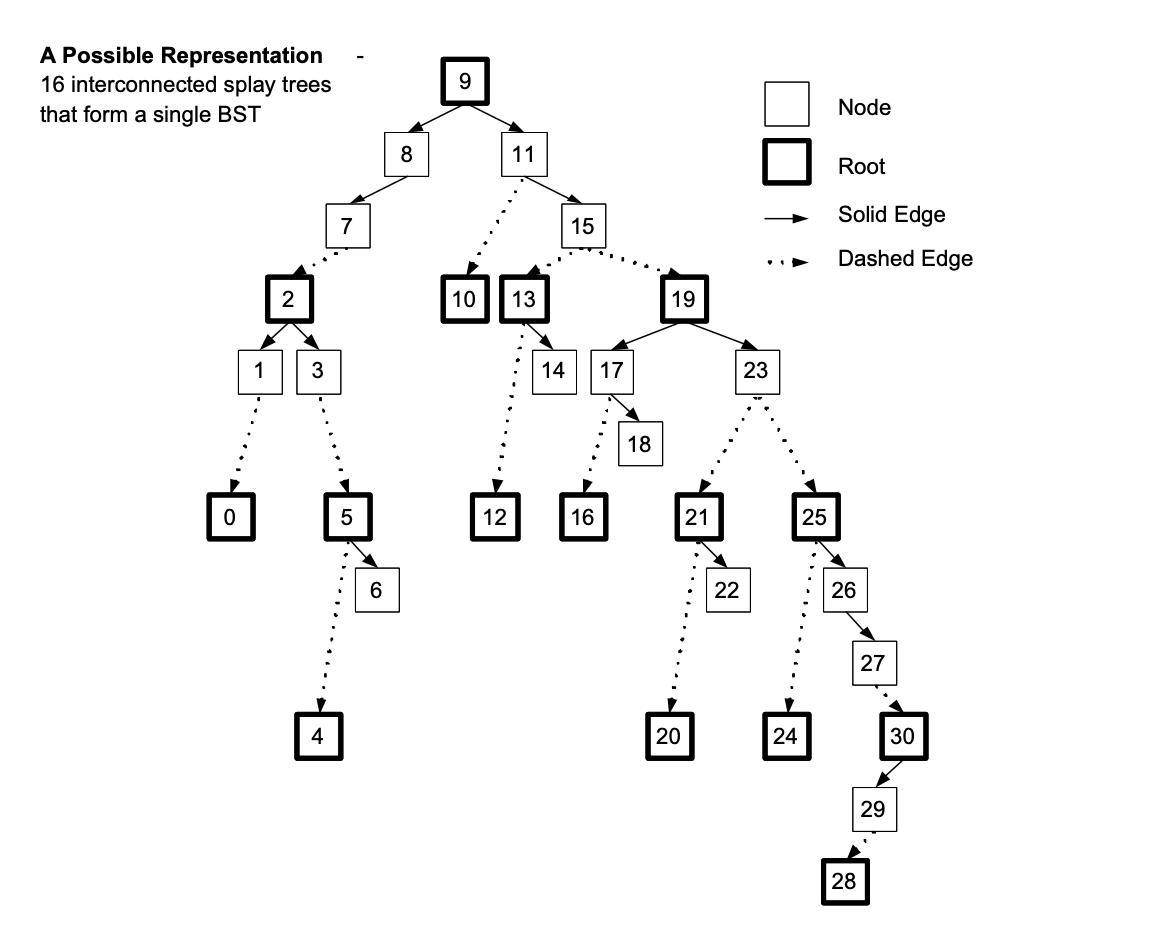
Source: Sleator and Wang 2004
Multi-splay implementation
Augmented tree (of splay trees) with Query method implemented
Only support static trees, augmentations depend on a perfect binary search tree
All modifications to the tree are made via splaying
Multi-splay Query implementation
Left2Right(node) and Right2Left(node) change the preferred child of node
Change the preferred children top-down and splay such nodes
Multi-splay benchmarks: sequential access
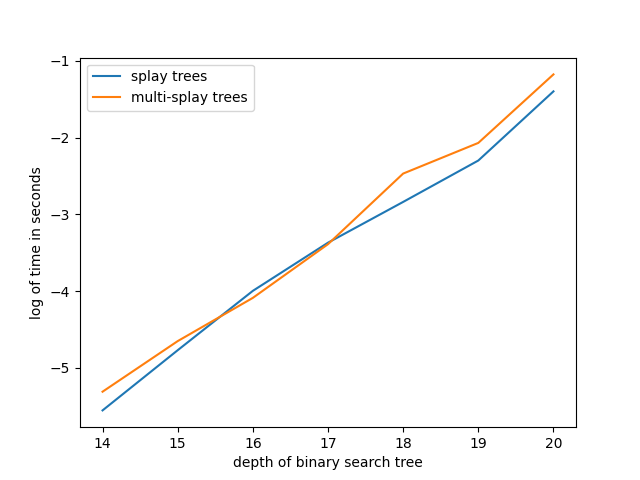
Multi-splay benchmarks: random access

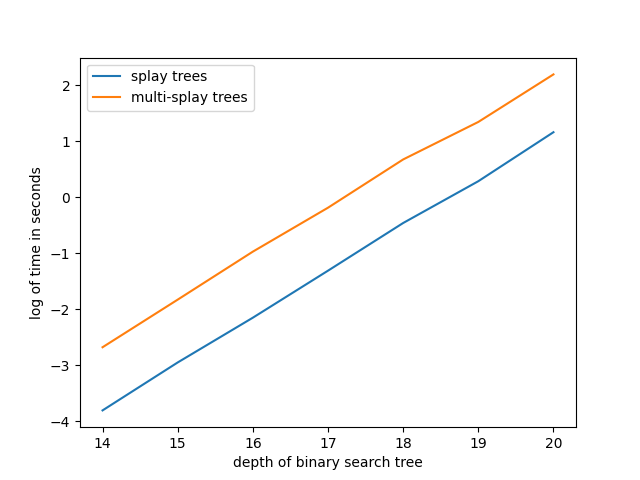
Multi-splay benchmarks: bit reversal sequence
Tango trees
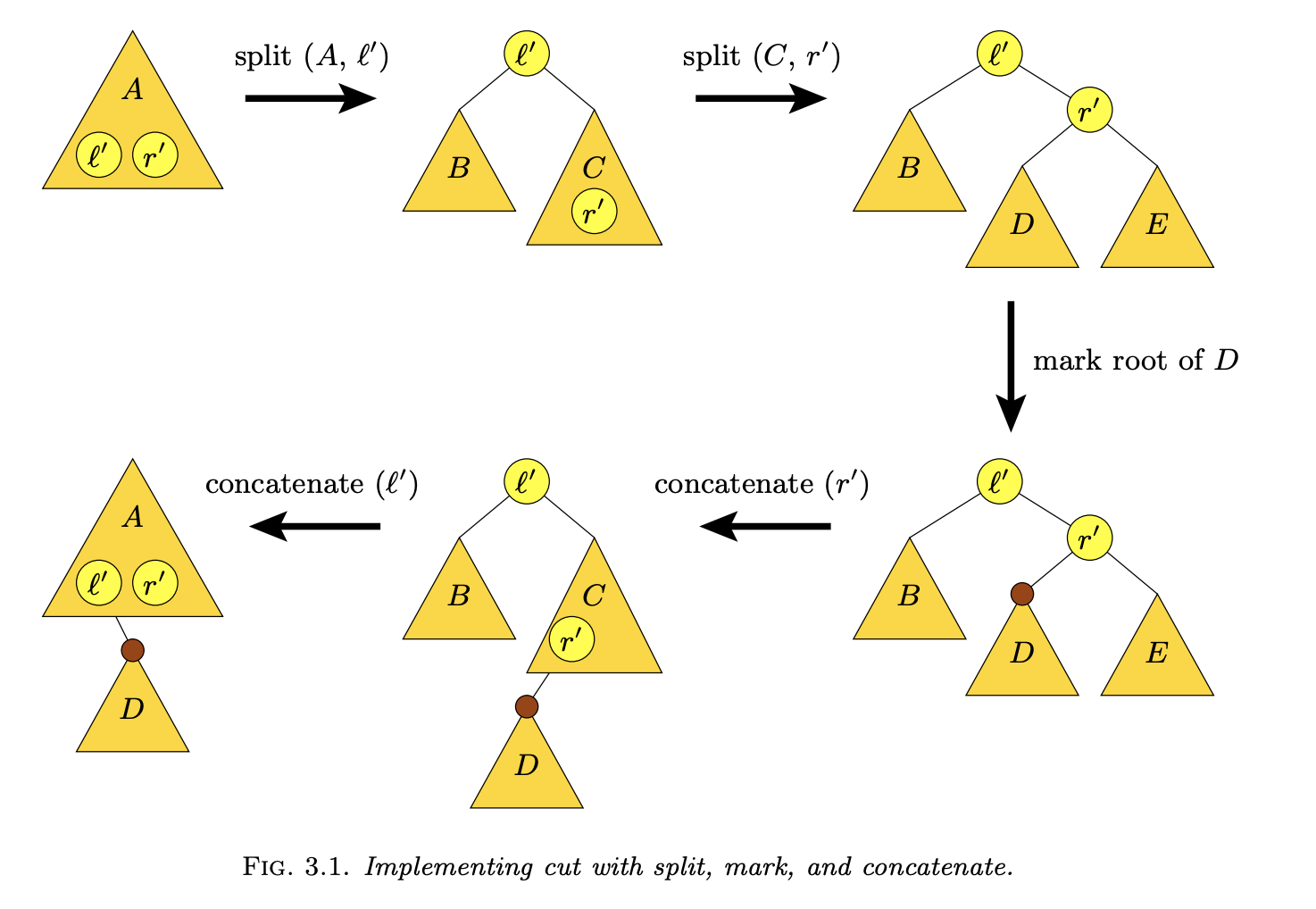
Source: Demaine et al. 2005
Tango implementation progress
Augmented red-black tree (of trees) with split/concatenate implemented
Challenge: the implicit tree-of-trees representation makes everything trickier!
API: lock() (read-only) and unlock() (write-only)
Tango implementation TODO
(Seemingly) need to implement perfect tree → tango tree conversion
After this, finishing cut/join should be relatively simple
Empirical work: benchmarks against multi-splay implementation and the like