Maths: Shapes

Dr. Paul Johnson

Paul

• Topology: what's leftover from Geometry if can't measure distance or angles
• Graph Theory: Studying how "things" are "connected"

Studying "Shapes"

Goal: Convince you these ideas are Fun and useful

Topology Joke

Henry Segerman

Videogames

Surface:

Locally looks 2-dimensional

Text

Manifold: 

Locally looks n-dimensional

 What n-dimensional manifolds are there?

How can we tell different manifolds apart?

What manifold do we live in?

M.C. Escher

Cosmic Microwave Background

Graph Theory:

"Utilities Puzzle"

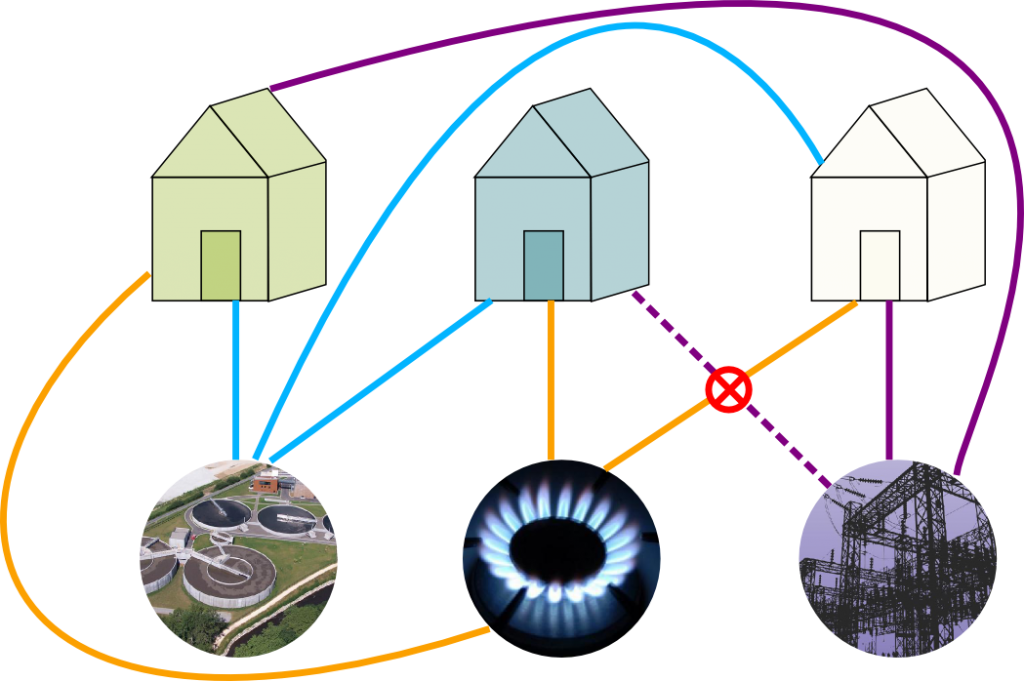
A failed attempt

Utilities question is impossible

But how can we know for sure?

How can we prove it?

Can we check every single possible way of connecting them, or are there infinite many different possibilities to try?

If it were possible, some connections would make a loop.

That loop would have an inside and an outside...

What connections are missing?

Utilities question is impossible

But how can we know for sure?

How can we prove it?

Can we check every single possible way of connecting them, or are there infinite many different possibilities to try?

If it were possible, some connections would make a loop.

That loop would have an inside and an outside...

This isn't true on the Mobius/Torus band!  Can we solve the Utilities Question there?

Solve it on the Mobius Band?

Graphs:

• Vertices: A set of "things"
• Edges: A set of "connections" between pairs of things

Text

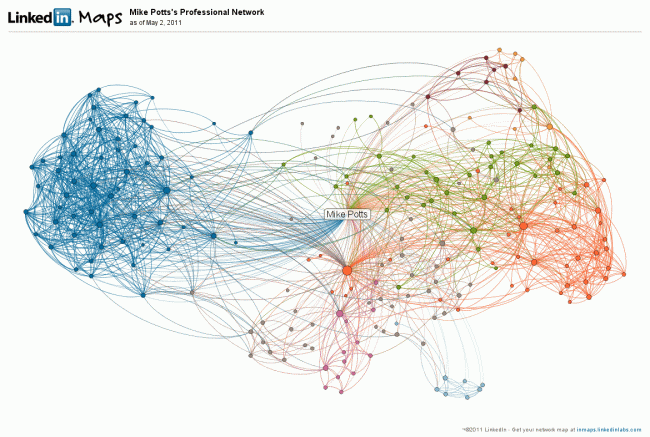
"Epidemic dynamics on higher-dimensional small world networks"

Figure from an applied math/biology paper

The same graph, drawn different ways

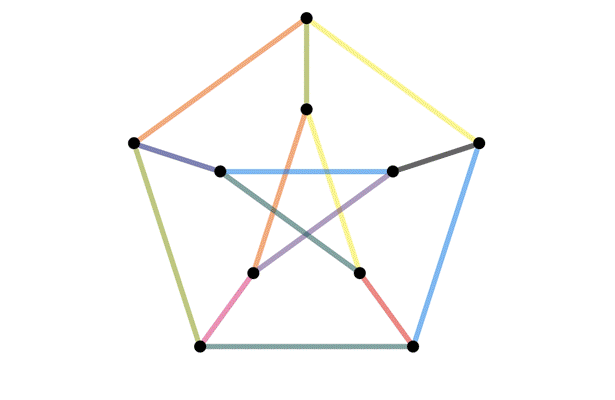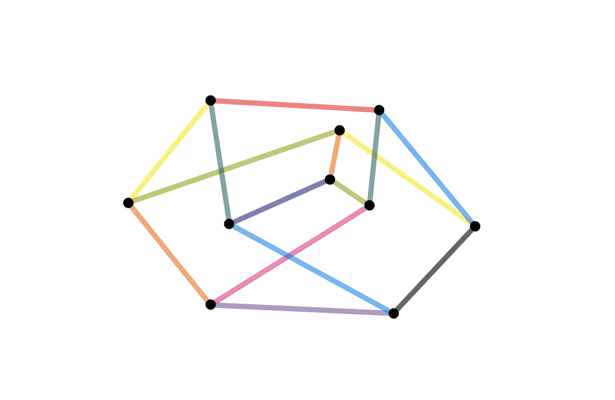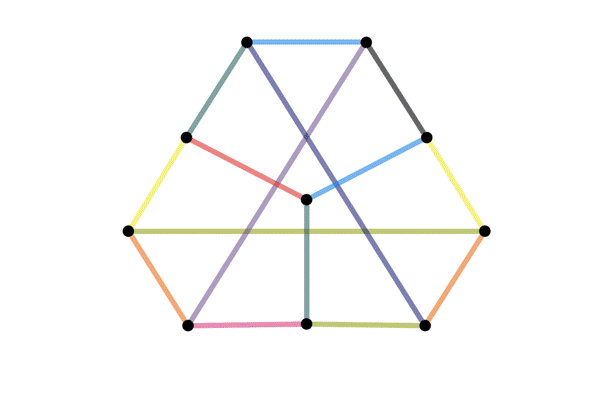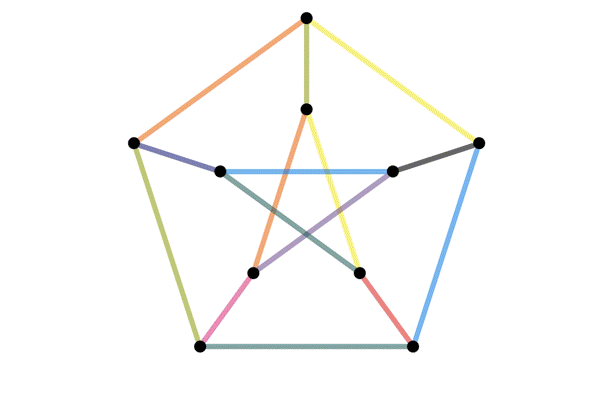
Definition: A graph is planar if it can be drawn on a piece of paper without any edges crossing.

Definition: The complete graph on n vertices, written \(K_n\), is the graph with n vertices, and an edge between every pair of vertices

Definition: The complete bipartite graph \(K_{n,m}\) has n red vertices, m blue vertices, and an edge between every red vertex and every blue vertex.

Utilities Question: Is \(K_{3,3}\) planar?

What about other graphs?

Can you draw this graph on the Mobius Band?