計算幾何
Computational Geometry
建國中學 吳沛恩
目錄
- 座標與向量
- 有向面積
- 線段相交
- 掃描線算法
- 極角排序
- 凸包演算法
- 旋轉卡尺
- 模擬退火
- More Topics
「計算幾何是以數學方式精確與高效的計算出幾何結構與其性質的嚴謹應用。」
今天討論的都是二維平面上的幾何問題!
座標與向量
線性代數
座標


- 二維平面座標
- 極座標
Source: Wiki
Source: Wiki
實作上的座標
template <typename T>
class pt{
T x,y;
//下方運算子重載與上方相同
}
pt<int> p[N]; //點座標宣告為整數
pt<double> pp[N]; //點的不同資料型別宣告依照題目需求,座標可以用int或double存
廣義三角函數

Source: https://pse.is/3suhzc
弧度
- \(2\pi = 360^{\circ},\pi = 180^{\circ}\)
- \(x = \frac{x^{\circ}}{180}\times\pi\)
- \(x^{\circ} = \frac{x}{\pi}\times 180^{\circ}\)
- 弧度沒有單位,以「rad」表示!
- C++ 裡面的三角函數都是弧度!

Source: Wiki
三角函數運算
等一下證明會用到
- 平方關係:\(\sin^2\theta +\cos^2\theta = 1\)
- 正弦定理:\(\frac{c}{\sin(\gamma)} = \frac{a}{\sin(\alpha)} = \frac{b}{\sin(\beta)}\)
- 餘弦定理:\(cos(\gamma) = \frac{a^2+b^2-c^2}{2ab}\)

向量
- 有向線段(向:方向、量:長度)
- 純量:只有大小、沒有方向的量
- \(\overrightarrow{AB}\):由 A 點起始指向 B 點的向量
- 可任意移動
- 向量長度(加絕對值表示):兩點的歐基里德距離
- \(\left|\overrightarrow{AB}\right| = \sqrt{{(x_A - x_B)}^2 + {(y_A - y_B)}^2}\)
Vector
向量加法
- 頭尾相連:\(\overrightarrow{AC} = \overrightarrow{AB}+\overrightarrow{BC}\)
- 三角形法
- 平行四邊形法
EX:
=
+
(2,1)
(2,0)
(0,1)

EX:
向量減法
終點減始點
內積(DOT)
Dot Product
定義:若 \(\vec a\) 與 \(\vec b\) 為二度或三度空間的向量,且 \(\theta\) 為\(\vec a\) 與 \(\vec b\) 的夾角(滿足\(0\leq\theta\leq\pi\)),則點積(或歐基里德內積 ) \(\vec a\cdot\vec b\) 定義為
內積(DOT)
Dot Product
- 直觀看法:兩個向量在「同一方向」的程度
- 兩個向量的內積(點積)以「\(\cdot\)」表示
- 運算結果為一個純量
- 幾何關係:\(\vec A\cdot \vec B = |\vec A||\vec B|\cos\theta\)
- 正定性:\(|\vec A|^2 = \vec A\cdot\vec A\)
- 座標公式:假設\(A(x_A,y_A),B(x_B,y_B)\),則內積滿足:\(\vec A\cdot\vec B = x_Ax_B+y_Ay_B\)

Source: Wiki
內積(DOT)
Dot Product
- \(\vec A\cdot\vec B > 0\):兩向量之間的夾角為銳角
- \(\vec A\cdot\vec B = 0\):兩向量垂直
- \(\vec A\cdot\vec B < 0\):兩向量夾角為鈍角



Proof
令向量\(\overrightarrow{a} = (x_1,y_1),\overrightarrow{b} = (x_2,y_2)\),證明:
餘弦定理:\(\cos\theta = \frac{|\vec a|^2+|\vec b|^2-|\vec a-\vec b|^2}{2|\vec a||\vec b|}\),帶入公式:
外積(CROSS)
Cross product
定義:若\(a = (a_1,a_2,a_3)\)與\(b = (b_1,b_2,b_3)\)為三度空間裡的向量,則外積(叉積)\(a\times b\) 為一向量定義為:
向量的外積只有在三度空間才有定義!
外積結果的向量由右手定則決定
外積(CROSS)


Cross product
- 直觀看法:兩向量在逆時針方向的「垂直」的程度
- 兩個向量的外積(叉積)以「\(\times\)」表示
- 幾何關係:\(\vec A\times \vec B = \hat n|\vec A||\vec B|\sin\theta\)(\(\theta\)為有向角)
- 運算結果為一個向量(三維空間),方向由右手定則決定
- 外積結果同時也是兩向量所張的平行四邊形面積,我們在二維平面上將它拿來當作純量來使用
- 座標公式:假設\(A(x_A,y_A),B(x_B,y_B)\),則外積滿足:\(\vec A\times\vec B = x_Ay_B-x_By_A\)
Source: Wiki
Source: Wiki
外積(CROSS)
Cross product
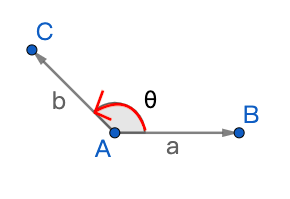
- \(\vec A\times\vec B > 0\):A向量到B向量逆時針旋轉
- \(\vec A\times\vec B = 0\):兩向量平行
- \(\vec A\times\vec B < 0\):A向量到B向量順時針旋轉


Proof
令向量\(\vec{a} = (x_1,y_1),\vec{b} = (x_2,y_2)\),證明:
得到:\(\vec a\times\vec b = x_1y_2-x_2y_1\)
比較
- 向量內積(Dot Product)
- 判斷向量是否垂直
- 結果為純量
- 向量外積(Cross Product)
- 判斷向量是否平行
- 結果為向量(今天都當純量來用)
- 判斷向量夾角方向
- 可用來計算面積
實作上的向量
struct pt{
int x,y;
bool operator < (pt b){
if(x == b.x)return y < b.y;
return x < b.x;
}
bool operator > (pt b){
if(x == b.x)return y > b.y;
return x > b.x;
}
bool operator == (pt b){
if(abs(x-b.x)<=eps && abs(y-b.y)<=eps)return true;
return false;
}
pt operator+(pt b) {return {x + b.x, y + b.y};} //向量相加
pt operator-(pt b) {return {x - b.x, y - b.y};} //向量相減
pt operator*(int k) {return {x * k, y * k};} //向量乘法(係數積)
pt operator/(int k) {return {x / k, y / k};} //向量除法
int operator^(pt b) {return x * b.y - y * b.x;} //向量外積cross
int operator*(pt b) {return x * b.x + y * b.y;} //向量內積dot
};題目
-
Leetcode:223. Rectangle Area
- 給定平面上兩個矩形,求交集面積
-
Leetcode:939. Minimum Area Rectangle
- 給定平面上\(n\)個點,求由這些點構成的最小矩形面積(邊平行於\(x-y\)軸)
-
Leetcode:963. Minimum Area Rectangle II
- 續上題,邊可能不平行於\(x-y\)軸
-
NEOJ 399:等長線段對
- 給定平面上很多個點,求出有幾對線段等長。
有向面積
好用的工具
性質
- 利用外積計算多邊形面積
- 有向角:逆時針為正、順時針為負
- 外積有正有負,稱為「有向面積」
+
-
三角形面積
兩向量夾出的三角形有向面積為:
A
B
C
三角形面積
代數證明:利用正弦三角形面積公式推得
三角形面積
幾何證明:簡單明瞭

多邊形面積
- 在平面上任選一點(通常是原點)
- 以此點為一端點,將多邊形切割成許多三角形。
- 依照逆時鐘的方向將所有三角形的有向面積相加即是多邊形的有向面積。

Source: https://reurl.cc/NZ5ZNq
多邊形面積
假設多邊形的頂點依序為(要特別注意結束的點必須是起始點):
則多邊形的面積為(aka測量師公式):
多邊形面積

Pick's Theorem
給定頂點座標均是格子點的簡單多邊形,皮克定理說明了其面積\(A\)和內部格點數目\(i\)、邊上格點數目\(b\)的關係:
證明在這裡
Pick's Theorem

Source: Wiki
題目
-
ZJ a871: Museum Area
- n個點圍成的多邊形,求面積。
-
CSES: Polygon Area
- 一樣是裸題
-
Polygon Lattice Points
- 裸皮克定理
線段相交
線段香蕉
方向函式
- 利用外積找兩向量相對的方向,方便判斷
- 共線則為回傳0,逆時針回傳1,順時針回傳-1
//方向函數dir,回傳OA向量與OB向量的方向
int dir(pt a, pt b, pt o) { //方向函數
int cross = (a - o) ^ (b - o);
if(fabs(cross) <= eps) return 0;
else if(cross > 0) return 1;
else return -1;
}方向函式
方向函式能做什麼?

判斷點是否在線段兩端點的異側!
點與線段的關係
- 判斷線段
香蕉之前,先處理點在線段上的情況 - onseg() 判斷點 O 是否在線段 AB 之上
- 當點在線段上時,OA向量與OB向量之外積為零、內積為負(夾角為180度)
bool onseg(pt a, pt b, pt o){ //o是否在ab線段上
int cross = (a - o) ^ (b - o); //是否平行
int dot = (a - o) * (b - o); //是否在線段中
return (cross == 0)&&(dot <= 0);
}線段相交
- 首先判斷特例,也就是線段有一端點在另外線段上
- 利用方向函式判斷點是否在另一線段端點的異側
bool Intersection(pt a, pt b, pt c, pt d){ //線段ab是否與cd相交
if(onseg(a,b,c)||onseg(a,b,d))return true; //點c、d是否洽在線段ab上
if(onseg(c,d,a)||onseg(c,d,b))return true; //點a、b是否洽在線段cd上
if(dir(a,b,c)*dir(a,b,d)==-1 && dir(c,d,a)*dir(c,d,b)==-1)
return true; //對於線段兩端點看另外兩端點必須方向相反
return false;
}線段交點座標
知道兩線段是否相交之後,進一步求出交點座標

線段交點座標
幾個算式列一列得到:
帶回 \(\vec{P} = \vec{A} + i\overrightarrow{AB}\) 即可
pt Intersection_point(pt a, pt b, pt c, pt d){
assert(Intersection(a, b, c, d)); //是否相交
return a + ((a - c)^(d - c) * (b - a))/((d - c)^(b - a));
}Point in Polygon
給定平面上\(n\)個點構成的簡單多邊形,還有\(m\)個詢問的點。對每一個點輸出它是在多邊形內部、外部或邊界上。
$$3\leq n\leq 1000$$
$$1\leq m\leq 1000$$
$$10^9\leq x_i,y_i\leq 10^9$$
來看看凸多邊形的情況
- 由P點指向多邊形上點的向量依序繞一圈做外積,過程中結果皆為正,表示在多邊形內部。


- 若遇到凹多邊形,則這個方法會失敗。
射線作法
- 對每一個點做一條往正x方向的射線(實作上就是和一個x座標很大的點,連成線段)
- 計算每一條邊與這條線段相交的次數。
- 如果是奇數則在多邊形內部,反之則是在外部。
- 小心處理相交於多邊形頂點的情況
- 相交頂點時只考慮 \(y\) 較小的點
- 把射線改成往右上角斜?
- 右端點設成\((\infty,y_i+1)\)

Source: geeksforgeeks
程式碼
#include <bits/stdc++.h>
#define int long long
#define double long double
#define pii pair<int, int>
#define N 1005
#define INF 1000000005
#define x first
#define y second
#define IOS ios::sync_with_stdio(0),cin.tie(0)
using namespace std;
int n,m;
struct point{
int x,y;
bool operator == (point b){
if(x == b.x && y == b.y)return true;
return false;
}
point operator - (point b){return {x - b.x , y - b.y};}
point operator + (point b){return {x + b.x , y + b.y};}
int operator ^ (point b){return (x * b.y - y * b.x);}
int operator * (point b){return (x * b.x + y * b.y);}
}pt[N];
bool onseg(point a,point b,point o){
int cross = (a - o) ^ (b - o);
int dot = (a - o) * (b - o);
return (cross == 0) && (dot <= 0);
}
int dir(point a,point b,point o){
int cross = (a - o) ^ (b - o);
if(cross == 0)return 0;
else if(cross > 0)return 1;
else return -1;
}
bool inter(point a,point b,point c,point d){
if(onseg(a,b,c) || onseg(a,b,d))return true;
if(onseg(c,d,a) || onseg(c,d,b))return true;
if(dir(a,b,c) * dir(a,b,d) < 0 && dir(c,d,a) * dir(c,d,b) < 0)
return true;
return false;
}
int solve(point cur){
int sum = 0;
for(int i=0;i<n;i++){
if(onseg(pt[i],pt[i+1],cur) == 1)return -1;
if(inter(pt[i],pt[i+1],cur,point{INF,cur.y}))sum++;
point temp = pt[i].y > pt[i+1].y ? pt[i] : pt[i+1];
if(temp.y == cur.y && temp.x > cur.x)sum--;
}
return sum;
}
signed main(){
IOS;
cin>>n>>m;
for(int i=0;i<n;i++)cin>>pt[i].x>>pt[i].y;
pt[n] = pt[0];
for(int i=0;i<m;i++){
point temp;cin>>temp.x>>temp.y;
int ans = solve(temp);
if(ans == -1)cout<<"BOUNDARY"<<"\n";
else if(ans & 1)cout<<"INSIDE"<<"\n";
else cout<<"OUTSIDE"<<"\n";
}
}
題目
-
NEOJ 400:向左轉向右轉
- 給你平面上n個點,依序走訪每一個點,試問走訪過程中共執行幾次的左轉、右轉以及迴轉。
-
CSES 2190:Line Segment Intersection
- 裸的線段相交
-
NEOJ 401:線段相交
- 裸的線段相交
掃描線算法
好用的工具
給定平面上\(n\)個點的座標\((x_i, y_i)\)
求出這 \(n\) 個點中最近的兩個點的距離是多少?
\(n \leq 50000, x_i, y_i \leq 2^{31} - 1\)
註:這邊的距離指的是歐幾里得距離
經典題1:最近點對問題
四種不同作法
- 暴力,極度慢:\(O(n^2)\)
- 掃描線,很快:\(O(n\log n)\)
- 分治,之前講過:\(O(n\log n)\)
- 隨機,實作複雜:期望\(O(n)\)
這裡有更詳盡的比較
今天要講的是掃描線算法
作法1
- 先將所有點依照 \(x\) 座標進行排序
- 想像一條從左往右掃的掃描線,對於每一條掃描線看右邊的點,如果當前最近點對距離為 \(d\),只要遇上x座標差距大於 \(d\) 的點時,即可繼續下一輪的枚舉。
複雜度分析:Worst Case : \(O(n^2)\)
當所有點都在同一鉛直線上會退化成平方
作法1

如何處理點集中在鉛直線上的情況?
作法2
- 利用set優化作法1
- 左掃描線依序往右掃(作法1是右掃描線)
- 用二分搜把y座標範圍在\(d\) 之內的點挑出來
- 複雜度:\(O(n\log n)\)
作法2
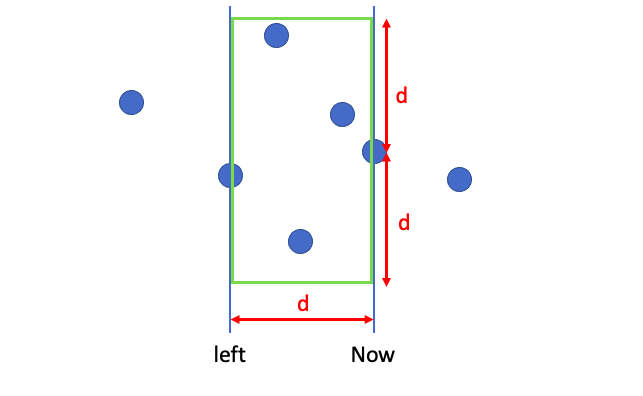
- 將點輸入並且排序,X座標為主,Y座標為輔。
- 使用set,並以Y座標為排序基準,以儲存第\(i\)點的左方、水平距離小於等於 \(d\) 的點。
- 右掃描線依序窮舉各點作為右端點。
- Erase與右端點水平距離大於 \(d\) 的點們(左掃描線右移)
- 用二分搜找出與第 \(i\) 點垂直距離小於 \(d\) 的點,並嘗試更新
- 將第 \(i\) 點加入set中。
作法2
作法2:實作
#include <bits/stdc++.h>
#define int long long
#define ld long double
#define N 200005
#define x first
#define y second
#define pii pair<int,int>
#define IOS ios::sync_with_stdio(0),cin.tie(0)
using namespace std;
int n;
vector<pii> p;
set<pii> s;
ld dis(pii a, pii b){
ld x = a.x-b.x, y = a.y-b.y;
return sqrt(x*x + y*y);
}
signed main(){
IOS;
cout<<fixed<<setprecision(6);
while(cin>>n){
p.assign(n,{0,0});
for(int i = 0;i < n;i++)cin>>p[i].x>>p[i].y;
sort(p.begin(),p.end());
s.clear();
s.insert({p[0].y,p[0].x});
int l = 0;ld ans = 5e18;
for(int i = 1;i < n;i++){
int d = ceil(ans);
while(l < i && p[l].x < p[i].x - d){
s.erase({p[l].y,p[l].x});
l++;
}
auto it_l = s.lower_bound({p[i].y - d,0});
auto it_r = s.upper_bound({p[i].y + d,0});
for(auto it = it_l;it != it_r;it++){
ans = min(ans,dis({it->y,it->x},p[i]));
}
s.insert({p[i].y,p[i].x});
}
cout<<ans<<endl;
}
}經典題2:矩形合併面積計算
給你一堆矩形,找出他們覆蓋範圍的總面積
(這一題在之前資料結構那邊講過)
\(n \leq 10^5\), 矩形範圍 \(\leq 10^6\)

Source: OI-wiki
題目
極角排序
逆時鐘一個一個排
Polar coordinate system
利用每一個對特定點(通常是原點)的極座標的角度進行排序

C++ 三角函數
- 用 asin(),acos() 常常有值域的問題
- 用 atan2() 很棒!
- 值域 \((-\pi,\pi]\),可以換算成0~360度

Source: Wiki
應用問題
- 點集共線問題
- 點集能構成多少個三角形
- 常常搭配雙指針找範圍
Sort by Angle
- 優點:直觀
- 缺點:慢、浮點數誤差
- 利用\(atan2(y,x)\)求出角度
bool cmp(pt a, pt b){
return atan2(a.y,a.x) < atan2(b.y,b.x);
}
sort(p.begin(),p.end(),cmp);Sort by Cross
- 利用有向角的正負決定前後順序
- 因為外積的夾角都是銳角,不能直接Cross,要先判斷點在左或右半平面
bool cmp(pt a, pt b){
bool f1 = a < pt{0,0};
bool f2 = b < pt{0,0};
if(f1 != f2)return f1 < f2;
return (a ^ b) > 0;
//逆時針將點進行極角排序,從270度開始逆時針
}
sort(p.begin(),p.end(),cmp);
//以id為原點進行極角排序TIOJ 1205 直角三角形
給你 \(N\) 個座標平面上的點\((x_i,y_i)\),請問總共可形成多少個直角三角形呢?
\(3\leq N \leq 1500, -10^9\leq x_i,y_i\leq 10^9\)
註:保證同一座標不會有兩個點
想法
- 枚舉三角形的三個頂點,排除三點共線的情況,檢查兩兩線段夾的角度是不是直角。
- 複雜度:\(O(n^3)\)
- 可能會TLE,但時限7秒應該會過
- 極角排序?
- 枚舉每一個點當作原點,對所有點進行極角排序
- 預處理將所有共線的點縮成一點
- 雙指針走訪每一個點,與原點夾90度則答案加一
- 繞完一圈就結束了!
- 複雜度:\(O(n^2\log n)\)
程式碼
#include <bits/stdc++.h>
#define Orz ios::sync_with_stdio(0),cin.tie(0)
#define rep(i,a,b) for(int i=a;i<=b;i++)
#define pii pair<int,int>
#define pdd pair<double,double>
#define int long long
#define ll long long
#define ld long double
#define N 100001
#define all(x) x.begin(),x.end()
#define eps 1e-9
#define x first
#define y second
using namespace std;
struct pt{
int x,y;
bool operator < (pt b){
if(x == b.x)return y < b.y;
return x < b.x;
}
bool operator > (pt b){
if(x == b.x)return y > b.y;
return x > b.x;
}
bool operator == (pt b){
if(x-b.x == 0 && y-b.y == 0)return true;
return false;
}
pt operator+(pt b) {return {x + b.x, y + b.y};} //向量相加
pt operator-(pt b) {return {x - b.x, y - b.y};} //向量相減
int operator^(pt b) {return x * b.y - y * b.x;} //向量外積cross
int operator*(pt b) {return x * b.x + y * b.y;} //向量內積dot
};
vector<pt> p,temp,pp;
vector<int> cnt;
int n,ans = 0;
bool cmp(pt a, pt b){
bool f1 = a < pt{0,0};
bool f2 = b < pt{0,0};
if(f1 != f2)return f1 < f2;
return (a ^ b) > 0;
//逆時針將點進行極角排序,從270度開始逆時針
}
//O(n)枚舉每個點當直角情況
int solve(pt id){
pp.clear();cnt.clear();temp.clear();
for(pt i : p){
pt cur = i - id;
if(cur == pt{0,0})continue;
temp.push_back(cur);
}
sort(all(temp),cmp); //以id為原點進行極角排序
pp.push_back(temp[0]); //pp每一角度只存至多一個點
cnt.push_back(1); //考慮每個點共線情況
int len = temp.size();
rep(i,1,len-1){
int cross = temp[i]^temp[i-1],dot = temp[i]*temp[i-1];
if(cross == 0 && dot >= 0)cnt[cnt.size()-1] += 1; //共線數量+=1
else {pp.push_back(temp[i]);cnt.push_back(1);} //非共線設定數量為1
}
len = pp.size(); //考慮橫跨一周的情況
rep(i,0,len-1){ //雙指針i,p1可能會超過一圈
pp.push_back(pp[i]); //將點再繞一圈
cnt.push_back(cnt[i]);
}
int ans = 0,p1 = 0;
rep(i, 0, len-1){
while(p1 < i+len && (pp[i]^pp[p1]) >= 0 && (pp[i]*pp[p1]) > 0)p1 += 1;
//夾銳角的情況要p1+=1
if((pp[i]^pp[p1]) > 0 && (pp[i]*pp[p1]) == 0)ans += cnt[i]*cnt[p1];
//正向的直角三角形,若共線則兩者數量相乘
}
return ans;
}
signed main(){
Orz;
while(cin>>n){
if(n == 0)break;
p.assign(n,{0,0});
rep(i,0,n-1)cin>>p[i].x>>p[i].y;
int ans = 0;
rep(i,0,n-1){
ans += solve(p[i]);
}
cout<<ans<<endl;
}
}
Counting Triangles
給你二維平面上\(n\)個點(n≤2400),每一個點座標皆不相同,計算總共可以畫出多少個三角形?
$$-10^9\leq x_i,y_i\leq 10^9$$
想法
- 在任三點沒有共線的情況下,總共可以畫出 \(C_3^n\) 個三角形
- 如果有\(m\)個點共線(在其他點不共線的情況下),則會少掉 \(C_3^m\) 個三角形
- 對於每一個點進行極角排序,雙指針找共線的區間長度,總複雜度\(O(n^2\log n)\)
- 把點全部移到上半平面較好處理!
程式碼
#include <bits/stdc++.h>
#define Orz ios::sync_with_stdio(0),cin.tie(0)
#define rep(i,a,b) for(int i=a;i<=b;i++)
#define pii pair<int,int>
#define pdd pair<double,double>
#define int long long
#define ll long long
#define ld long double
#define N 100001
#define all(x) x.begin(),x.end()
#define eps 1e-9
#define x first
#define y second
using namespace std;
struct pt{
int x,y;
bool operator < (pt b){
if(x == b.x)return y < b.y;
return x < b.x;
}
bool operator > (pt b){
if(x == b.x)return y > b.y;
return x > b.x;
}
bool operator == (pt b){
if(x-b.x == 0 && y-b.y == 0)return true;
return false;
}
pt operator+(pt b) {return {x + b.x, y + b.y};} //向量相加
pt operator-(pt b) {return {x - b.x, y - b.y};} //向量相減
int operator^(pt b) {return x * b.y - y * b.x;} //向量外積cross
int operator*(pt b) {return x * b.x + y * b.y;} //向量內積dot
};
vector<pt> p;
vector<int> cnt;
int n,ans = 0;
bool cmp(pt a, pt b){
bool f1 = a < pt{0,0};
bool f2 = b < pt{0,0};
if(f1 != f2)return f1 < f2;
return (a ^ b) > 0;
//逆時針將點進行極角排序,從270度開始逆時針
}
//用cnt[i]統計區間長度為i的線段數量
void solve(pt id){
vector<pt> pp;
for(auto i : p){ //以id為原點
pt cur = i-id;
if(cur == pt{0,0})continue;
if(cur.y < 0){cur.x = -cur.x;cur.y = -cur.y;}
if(cur.x < 0 && cur.y==0){cur.x = -cur.x;}
pp.push_back(cur);
}
sort(all(pp),cmp); //將id當作原點進行排序
int p1 = 0,p2 = 0,len = pp.size(); //雙指針找共線區間
while(p1 < n-1){ //最大化區間
while(p2+1 < len && (pp[p1]^pp[p2+1]) == 0)p2++;
cnt[p2-p1+2]+=1;
p1 = p2+1;
}
}
signed main(){
Orz;
cin>>n;
p.assign(n,{0,0});
cnt.resize(n+1,0);
rep(i,0,n-1)cin>>p[i].x>>p[i].y;
rep(i,0,n-1)solve(p[i]);
int ans = (n*(n-1)*(n-2))/6;
rep(i,3,n)ans-=(cnt[i]*(i-1)*(i-2))/6;
cout<<ans<<endl;
}
Max Points on a Line
給定二維平面上\(n\)個點,問一條直線最多能穿越幾個點?
$$1\leq n\leq 300$$
$$-10^4\leq x_i,y_i\leq 10^4$$
想法
- 枚舉每兩個點構成的直線,接著看有多少點會落在這條直線上
- 複雜度:\(O(n^3)\)
- 類似上一題的作法,極角排序之後用雙指針找出共線的最大區間
- 複雜度:\(O(n^2\log n)\)
- 有沒有更好的作法?
- 把每一個點當作是原點,把其他的點與原點的斜率丟進hash當中,計算同一斜率上有最多點的個數
- 斜率可以用分數處理,用浮點數有誤差的問題
- 複雜度:\(O(n^2)\)
題目
-
Leetcode 1610:Maximum Number of Visible Points
- 平面上\(n\)個點,以及一個視野的角度,找出一次最大能看到多少個點。
凸包演算法
Convex Hull
凸包是什麼?
- 凸包是一個凸多邊形(convex polygon)
- 滿足內角都 \(\leq 180\)度的多邊形
- 可以包住平面上所有點

Source: Wiki
凸包演算法
凸包演算法有非常多種,今天介紹其中兩種:
- Gift wrapping (a.k.a. Jarvis march)
- Graham scan
- Quickhull
- Divide and conquer
- Monotone chain (a.k.a. Andrew's algorithm)
- Incremental convex hull algorithm
- Kirkpatrick–Seidel algorithm
- Chan's algorithm
Gift Wrapping Algorithm
(a.k.a. Jarvis' March Algorithm)
- 其實它就是暴力法!
- 從一個凸包上的頂點開始,順著外圍繞一圈(順時針逆時針都可以)
- 每當要尋找凸包上下一個點,則窮舉平面上的所有點,找出最外圍的點來包覆(用外積判斷)。
- 時間複雜度:\(O(nm)\),\(n\) 為平面上的點、\(m\) 為凸包上的點。

Source: Wiki
Gift Wrapping Algorithm
(a.k.a. Jarvis' March Algorithm)
#include <bits/stdc++.h>
#define Orz ios::sync_with_stdio(0),cin.tie(0)
#define rep(i,a,b) for(int i=a;i<=b;i++)
#define pii pair<int,int>
#define pdd pair<double,double>
#define int long long
#define ll long long
#define ld long double
#define N 100001
#define eps 1e-9
#define x first
#define y second
using namespace std;
struct pt{
int x,y;
bool operator < (pt b){
if(x == b.x)return y < b.y;
return x < b.x;
}
bool operator > (pt b){
if(x == b.x)return y > b.y;
return x > b.x;
}
bool operator == (pt b){
if(x-b.x<=eps && y-b.y<=eps)return true;
return false;
}
pt operator+(pt b) {return {x + b.x, y + b.y};} //向量相加
pt operator-(pt b) {return {x - b.x, y - b.y};} //向量相減
int operator^(pt b) {return x * b.y - y * b.x;} //向量外積cross
int operator*(pt b) {return x * b.x + y * b.y;} //向量內積dot
};
bool cmp(pt a, pt b){
if(a.x == b.x)return a.y < b.y;
return a.x < b.x;
}
vector<pt> p;
bool check(pt a,pt b,pt o){
int cross = (a - o)^(b - o);
return cross > 0;
}
int n,t;
vector<pt> convex_hull(){
vector<pt> hull;
if(n < 3)return hull;
int l = 0;
for(int i = 0;i < n;i++){
if(p[i].x < p[l].x)l = i;
}
int p1 = l,p2;
do{
p2 = (p1 + 1) % n;
for(int i = 0;i < n;i++){
if(check(p[i],p[p2],p[p1]))p2 = i;
}
hull.push_back(p[p1]);
p1 = p2;
}while(p1 != l);
return hull;
}
signed main(){
Orz;
cin>>n;
p.assign(n,{0,0});
rep(i,0,n-1)cin>>p[i].x>>p[i].y;
vector<pt> hull = convex_hull();
cout<<hull.size()<<endl;
}
Monotone chain
(a.k.a. Andrew's algorithm)
- Monotone chain = 單調鍊
- 凸包 = 下凸包 + 上凸包
- 對點維護一個單調隊列
- 解決了凸包有重疊的點、共線的點、退化成線段和點的情況。

Source: Wiki
Monotone chain
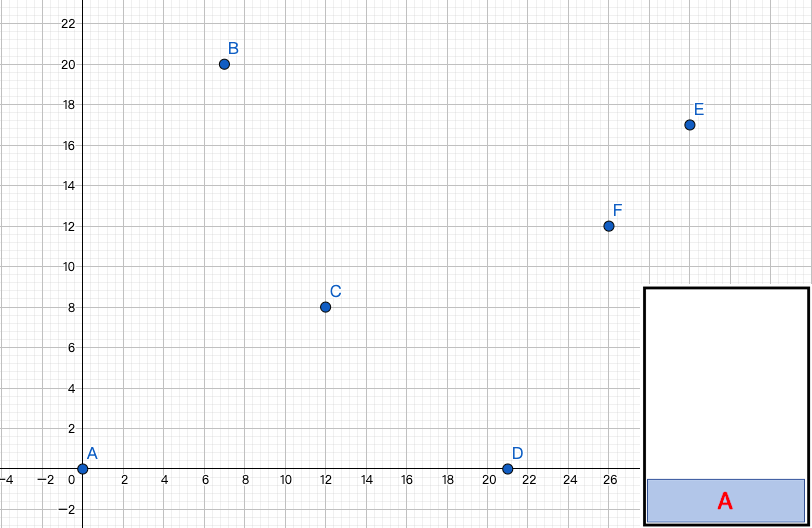
先把下半部凸包圍起來,上半部也可以照同樣方式圍出來。
- 對所有點的座標由x由小排到大
- 使用一個vector(功能為stack)紀錄當前凸包
- 檢查新加入的點會讓vector中哪些點不再是凸包上的點:假設單調隊列中末兩個點是\(P_{i-2},P_{i-1}\),則如果新加入的點\(P_i\)為凸包上的一點,則滿足:
4. 對點逆序之後把上凸包圍出來
Monotone chain

把小於零的點從vector中pop出來!
Monotone chain
Monotone chain

Monotone chain

Monotone chain

Monotone chain

Monotone chain

Monotone chain

將所有點reverse圍上凸包!
Monotone chain

Monotone chain

Monotone chain

Monotone chain

Monotone chain

Monotone chain

好欸,做完了!

程式碼
bool check(pt a, pt b, pt o){
pt aa = a - o;
pt bb = b - o;
return (aa ^ bb) >= 0;
}
vector<pt> convex_hull(){
vector<pt> hull;
sort(p.begin(),p.end(),cmp); //首先對x進行排序
for(auto i : p){ //依序走訪,如果遇到外積<0則不在凸包上
while(hull.size() > 1
&& check(i,hull[hull.size()-1],hull[hull.size()-2])){
hull.pop_back();
}
hull.push_back(i); //在凸包hull的每一點都符合外積小於0
}
int down_hull = hull.size();
hull.pop_back(); //x最大的點會在凸包上,不用做兩次先pop一次
reverse(p.begin(),p.end()); //將所有點逆序之後做一次上面的凸包
for(auto i: p){
while(hull.size() > down_hull
&& check(i,hull[hull.size()-1],hull[hull.size()-2])){
hull.pop_back();
}
hull.push_back(i);
}
return hull; //起點會經過兩次,剛好來算有向面積
}題目
- TIOJ 1178 Convex Hull
-
CSES 2195 Convex Hull
- 裸凸包
-
Leetcode 587 Erect the Fence
- 裸凸包(要輸出凸包邊上的點)
-
TIOJ 1280 領土 (Territory)
- 求所有點對連成的直線所能圍出的最大面積
-
TIOJ 1678 剪多邊形(molding)
- 求多邊形面積和凸包面積的差
旋轉卡尺
旋轉的卡尺
旋轉卡尺是什麼?

我們的多邊形

Source: Wiki
TIOJ 1105 H.PS3
給你一個平面上\(n\) 個點,求最遠點對。
$$2\leq n \leq 3000$$
$$0\leq x_i,y_y\leq 10^4$$
想法
- 其實\(n\)最大\(3000\)直接\(O(n^2)\)枚舉就好了!
- \(O(n\log n)\)?
- 先找出他們的凸包
- 旋轉卡尺夾著凸包,逆時鐘繞一圈,同時更新答案
- 複雜度:建立凸包\(O(n\log n)\),旋轉複雜度\(O(n)\)
如何旋轉?
- 紅色射線是卡尺的一端,我們可以觀察到凸包上的點到這條射線的距離呈現單峰函數
- 要找的點即是D點
- 什麼條件下卡尺能旋轉?點到直線的距離?
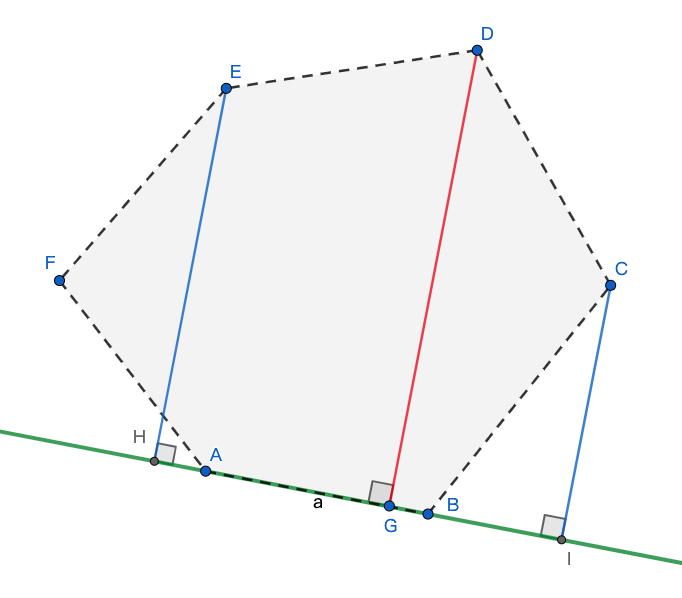
顯然太複雜了!
如何旋轉?

- 利用三角形面積判斷卡尺應不應該旋轉!
- 假設我們現在看的是點\(P\),則三角形面積:
- 不斷旋轉直到兩向量的外積結果有最大值(三角形面積最大)
程式碼
//省略找凸包的過程
bool check2(pt a,pt b,pt c,pt d){
int aa = abs((a - c)^(b - c));
int bb = abs((a - d)^(b - d));
return aa < bb;
}
void solve(){
int ans = 0,d = h,sz = hull.size();
rep(i,0,sz-1){
while(check2(hull[i],hull[(i+1)%sz],hull[d],hull[(d+1)%sz]))
d = (d+1)%sz;
ans = max(ans,(hull[i]-hull[d]).dis());
ans = max(ans,(hull[(i+1)%sz]-hull[d]).dis());
}
}題目
-
ZJ b288: 夏季大三角
- 平面上\(n\)個點,求最大三角形面積
- 練習\(O(n^2)\)的解法(雖然直接\(O(n^3)\)也會過)
- 在凸包上枚舉兩個點,用旋轉卡尺跟著第二個點往下轉找第三個頂點。
-
Ojdl 7083:龜兔賽多邊形
- 目前只有出題者過得了這一題XD
模擬退火(SA)
酷東西
模擬 退火?
- 它是一個隨機算法
- 用來尋找空間中近似最佳解
- 模擬金屬冶煉降溫的過程,初始高溫,在溫度慢慢下降過程當中,移動距離持續減小,直到停止在某一點。

Source: Wiki
利用模擬退火解決TSP
Leetcode 1515.
Best Position for a Service Centre
給你平面上\(n\)個點,請你找出一個點,使得這個點連到這 \(n\) 個點的距離總和最短。
\(n \leq 50, x_i,y_i \leq 100\)
想法
- 初始化
- 隨便戳一個點當作答案
- 設定一次要前進的長度 \(d\)
- \(d\) 一般以空間最長的長度來決定
- 迭代很多次(直到\(d\)小於題目給的精度)
- 隨便選擇一個方向,往那個方向走長度\(d\)
- 如果走到的點比現在好,則移動到那個點
- 否則縮短長度(\(d = d * 0.99\))
- 迭代很多次就是答案了!
程式碼(迭代1)
#define eps 1e-8
#define ld long double
#define pdd pair<ld,ld>
#define x first
#define y second
class Solution {
public:
pdd p[105];int n;
ld dis_all(pdd mid){
ld sum;
for(int i = 0;i < n;i++){
ld x = p[i].x - mid.x,y = p[i].y - mid.y;
sum += sqrt(x * x + y * y);
}
return sum;
}
double getMinDistSum(vector<vector<int>>& pos) {
srand(time(NULL));
n = pos.size();
for(int i = 0;i < n;i++)p[i] = {pos[i][0],pos[i][1]};
pdd cur = p[0];ld mid_dis = dis_all(p[0]);
ld test_size = 150.0;
while(test_size > eps){
pdd newp = cur;
int temp = rand();
newp.x += cos(temp) * test_size;
newp.y += sin(temp) * test_size;
ld new_dis = dis_all(newp);
if(new_dis < mid_dis){
mid_dis = new_dis;
cur = newp;
}
else test_size *= 0.99;
}
return mid_dis;
}
};程式碼(迭代2)
#define eps 1e-6
#define ld long double
#define pdd pair<ld,ld>
#define x first
#define y second
class Solution {
public:
pdd p[105];int n;
ld dis_all(pdd mid){
ld sum;
for(int i = 0;i < n;i++){
ld x = p[i].x - mid.x,y = p[i].y - mid.y;
sum += sqrt(x * x + y * y);
}
return sum;
}
double getMinDistSum(vector<vector<int>>& pos) {
n = pos.size();
for(int i = 0;i < n;i++)p[i] = {pos[i][0],pos[i][1]};
pdd cur = p[0];ld mid_dis = dis_all(p[0]);
ld test_size = 100;
ld dx[4] = {1.0,0.0,-1.0,0.0},dy[4] = {0.0,1.0,0.0,-1.0};
bool flag = 0;
while(test_size > eps){
flag = 0;
for(int i = 0;i < 4;i++){
pdd newp = cur;
newp.x += dx[i] * test_size;
newp.y += dy[i] * test_size;
ld new_dis = dis_all(newp);
if(new_dis < mid_dis){
mid_dis = new_dis;
cur = newp;
flag = 1;
break;
}
}
if(flag == 0)test_size /= 2.0;
}
return mid_dis;
}
};小問題
- 除了隨機找一個方向,也可以直接規定只能朝上下左右迭代(程式碼2)。
- 「當確定\(x\)坐標時,距離和函數對於\(y\)呈現單峰函數;當確定\(y\)坐標時,距離和函數對\(x\)呈現單峰函數。」
- 這一題在距離上有單調性,因此也有對\(x,y\)座標進行三分搜的解法。
題目
-
POJ - 2420 A Star not a Tree?
- 找出一個點,使得這個點連到這\(n\)個點的距離總和最短。
-
NEOJ 791 遊戲再度進行
- 給你一個圓和三角形,求出最大的交集面積。
- 難題不要輕易嘗試!
More Topics
More Topics
- Voronoi Diagram
- Delaunay Triangulation
- Bentley–Ottmann Algorithm
- 最小包覆圓
- 半平面交
- 反演變換