Asymptotic behavior of Brownian motion maximum log-likelihood means

Pernille E.H. Hansen

University of Copenhagen

Content of talk

Mean values on shape spaces
The BM-maximum likelihood mean
Law of Large Numbers
Central Limit Theorem
Example

Statistics on shape spaces

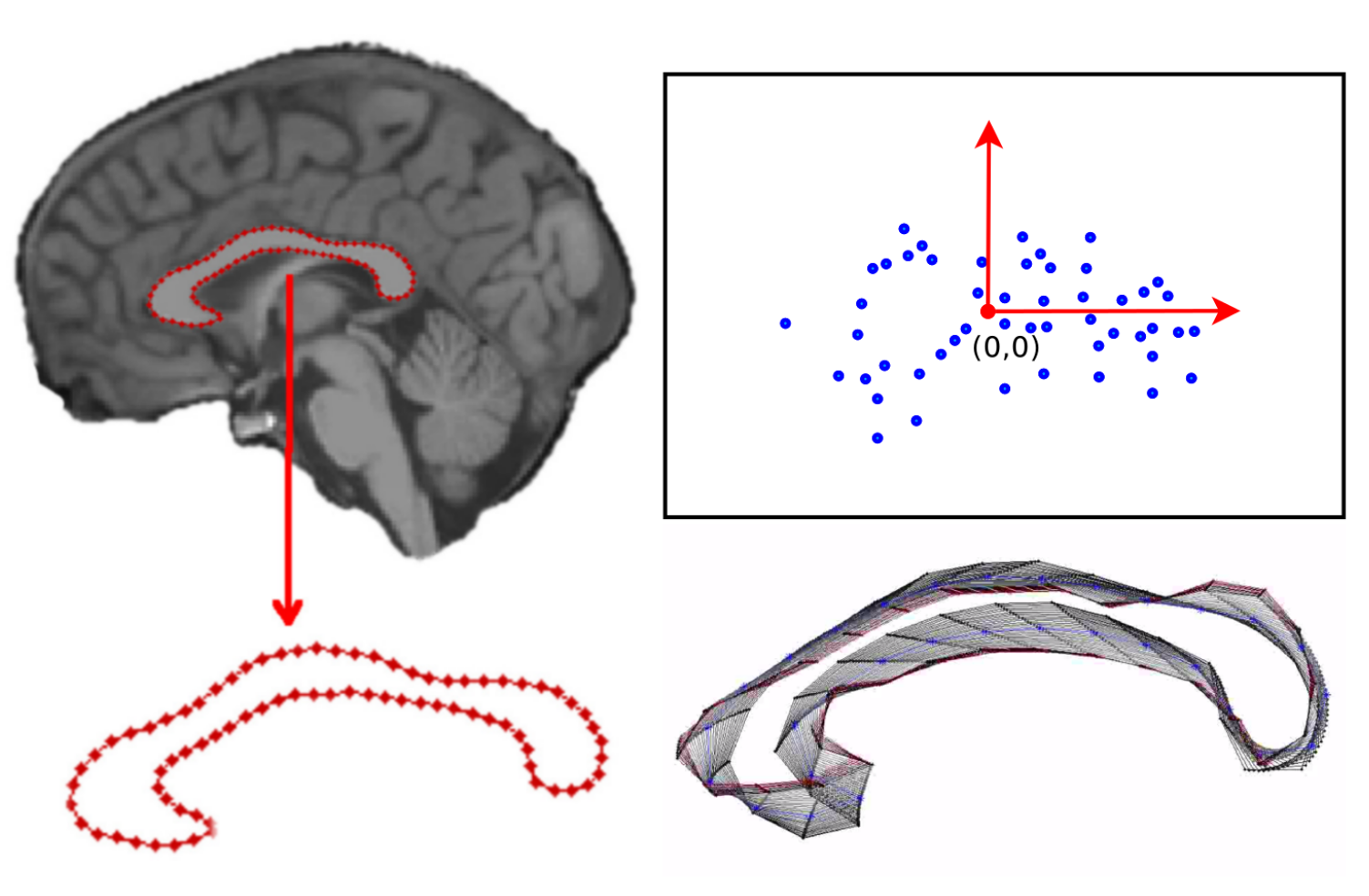
Medical Images

The sphere

\mathcal{S}^2

Manifolds

Mean value?

Y_1,...,Y_N\overset{\text{idd}}{\sim} Y \in

\mu = \mathbb{E}[Y]

Expected value:

Sample estimator:

\mu_N=\frac1N\sum_{i=1}^NY_i

Uniqueness, LLN, CLT

X_1,...,X_N\overset{\text{idd}}{\sim} X \in

\mathbb{R}^n

\mathbb{E}[X]

Fréchet mean

X:\Omega \to M

M = \arg\min_{y\in\mathcal{M}} \mathbb{E}[\text{dist}(y,X)^2]

The Riemann center of mass of a random variable is

If then is the Fréchet mean of

M = \{\mu \}

\mu

For , the sample Fréchet function

X_1,...,X_N\overset{\text{iid}}{\sim} X

F_N(y) = \frac{1}{N}\sum_{i=1}^{N} \text{dist}(y,X_i)^2

M_N = \arg\min_{y\in M}F_N(y)

and sample Fréchet means

Estimation

Uniqueness, LLN, CLT

Limitation:

\text{dist}:M\times M \to \R

is not smooth on all of

Brownian motion maximum log-likelihood means

Heat kernel on manifolds

p:M \times M \times \mathbb{R}_+ \to \mathbb{R}_+

is called a heat kernel on if

(\partial_t-\Delta_x)p(x,y,t) = 0

\lim_{t\to 0} p(x,y,t)= \delta_x(y)

M compact: Unique solution
Else: Unique minimal solution

t = 0.1

t = 0.5

t = 1

smooth manifold

A map

p \in \mathcal{C}^\infty

Brownian motion on manifolds

A Brownian motion on is a Markov process with transition density function

p(x,y,t) \approx

\text{"probability" of hitting }y

\text{ in time }t\text{ when starting in }x

p(x,y,t)

(B_t)

B_t = y

Brownian motion on manifolds

A Brownian motion on is a Markov process with transition density function

p(x,y,t) \approx

\text{"probability" of hitting }y

\text{ in time }t\text{ when starting in }x

p(x,y,t)

(B_t)

X_1,...,X_n \overset{\text{iid}}{\sim}X\in M

Given

\mu = -\arg\min \mathbb{E}_X[\ln p(x,X,t)]

mean point of

\mu = \arg\max \frac{1}{n} \sum_{i=1}^n \ln(p(x,X_i,t))

most likely origin points of

(B_t)

Brownian motion maximum log-likelihood mean

X:\Omega \to \mathcal{M}

E_t = \arg\min_{y\in\mathcal{M}} \mathbb{E}[-\text{ln }p(X,y,t)]

For , the (BMML)-likelihood means of a random variable

are the minimizers of the likelihood function

t>0

E_t

L_t(y) = \mathbb{E}[-\text{ln }p(X,y,t)]

\lim_{t\to 0} -t\ln p (x,y,t) = \frac{\text{dist}(x,y)^2}{2}

Estimation

L_{t,n}(x) = -\frac{1}{N}\sum_{i=1}^N\ln p(x,X_i,t)

E_{t,n} = \arg\min_{x\in M} L_{t,n}(x)

For the sample likelihood function is

X_1,...,X_n \overset{\text{idd}}{\sim} X

with sample likelihood means

Can we say something about:

(LLN)
(CLT)

\mu_n \overset{\mathbb{P}}{\to} \mu

\sqrt{n}(\mu_n-\mu)\overset{\mathcal{D}}{\to} D

\mu_{t,n}\in E_{t,n}

measurable selection.

Fix

t>0.

Law of large numbers

Fix

t>0.

(ZC) of Ziezold if

(E_{t,n})

\cap_{n=1}^\infty \overline{\cup_{k=n}^\infty E_{t,k}} \subset E_t \quad a.s.

(BPC) Bhattacharya and Patrangenaru if

\forall \epsilon>0 \exist n\in \mathbb{N}:

\cup_{k=n}^\infty E_{t,k} \subset B(E_t,\epsilon) \quad a.s.

\mu

\mu_n

\mu_{n-1}

We say that is a SCE in the sense of

Law of large numbers

Fix

t>0, \enspace M

\mu

\mu_n

\mu_{n-1}

satisfies (ZC) if either
- has compact support
- for all
satisfies (BPC) if
- satisfies (ZC)
- Heine-Borel property of
- (A coercivity condition)

Riemannian manifold,

X: \Omega \to M

\mathbb{E}[-\ln p (x,X,t)]<\infty

x\in M

(E_{t,n})

\overline{\cup_{n=1}^\infty E_{t,n}}

E_t \neq \emptyset

(E_{t,n})

*(Huckemann, 2010)

compact Riemannian manifold

satisfies (ZC)
satisfies (BPC) if

E_t \neq \emptyset

(E_{t,n})

Central Limit Theorem

and Smeariness

Central limit theorem & smeariness

\sqrt{n}\mu_n \overset{\mathcal{D}}{\to} \mathcal{N}(\mu,\Sigma)

X_1,...,X_n \overset{\text{idd}}{\sim} X

on with

\mathbb{R}^m

smeary:

n^{\frac{1}{2(k+1)}}X_n \overset{\mathcal{D}}{\to} \mathscr{L}

Note: CLT 0-smeary

\Rightarrow

\mathbb{E}[X] = \mu,

\mu_n = \frac{1}{n}\sum_{i=1}^n X_i

CLT:

(X_n)\in \mathbb{R}^m

Central limit theorem & smeariness

(Y_n)

smeary

n^{\frac{1}{2(k+1)}}X_n \overset{\mathcal{D}}{\to} \mathscr{L}

on Riemannian manifold

Define

X_n = \phi(Y_n)-\phi(\mu)\in \R^m

Does it there exist st is ?

(\mu_{t,n})

k\geq 0

(Y_n)

smeary

\phi

\phi:U \to \mathbb{R}^m

Let be a chart with

\mu \in U

\Leftrightarrow

X_n

\Leftrightarrow

smeary

Central limit theorem

Fix

t>0, \enspace M

Riemannian manifold,

X: \Omega \to M.

(Uniqueness):
(LLN): satisfies (BCP):
(Taylor Expansion): There exist

E_t = \{\mu_t\}

\mu_{t,n}\overset{\mathbb{P}}{\to}\mu_t

L_t(\exp_{\mu_t}(x)) = L_t(\exp_{\mu_t}(0)) + \sum_{i=1}^m T_i |(Rx)_i|^r + o(||x||^r)

\geq 2, R\in\text{SO}(m), T_1,...,T_m\neq 0 \text{ st.}

Assume:

(E_{t,n})

(\mu_{t,n})

smeary

with

k = \quad-2

and

\mathscr{L} = \mathcal{N}

The Example

P(X\in \mathbb{L}) = \alpha

P(X = \mu) = 1-\alpha

\mu

What are the log-likelihood means and is the estimator smeary?

\alpha\in [0,1]

t>0

Does the answer depend on and ?

The Fréchet means

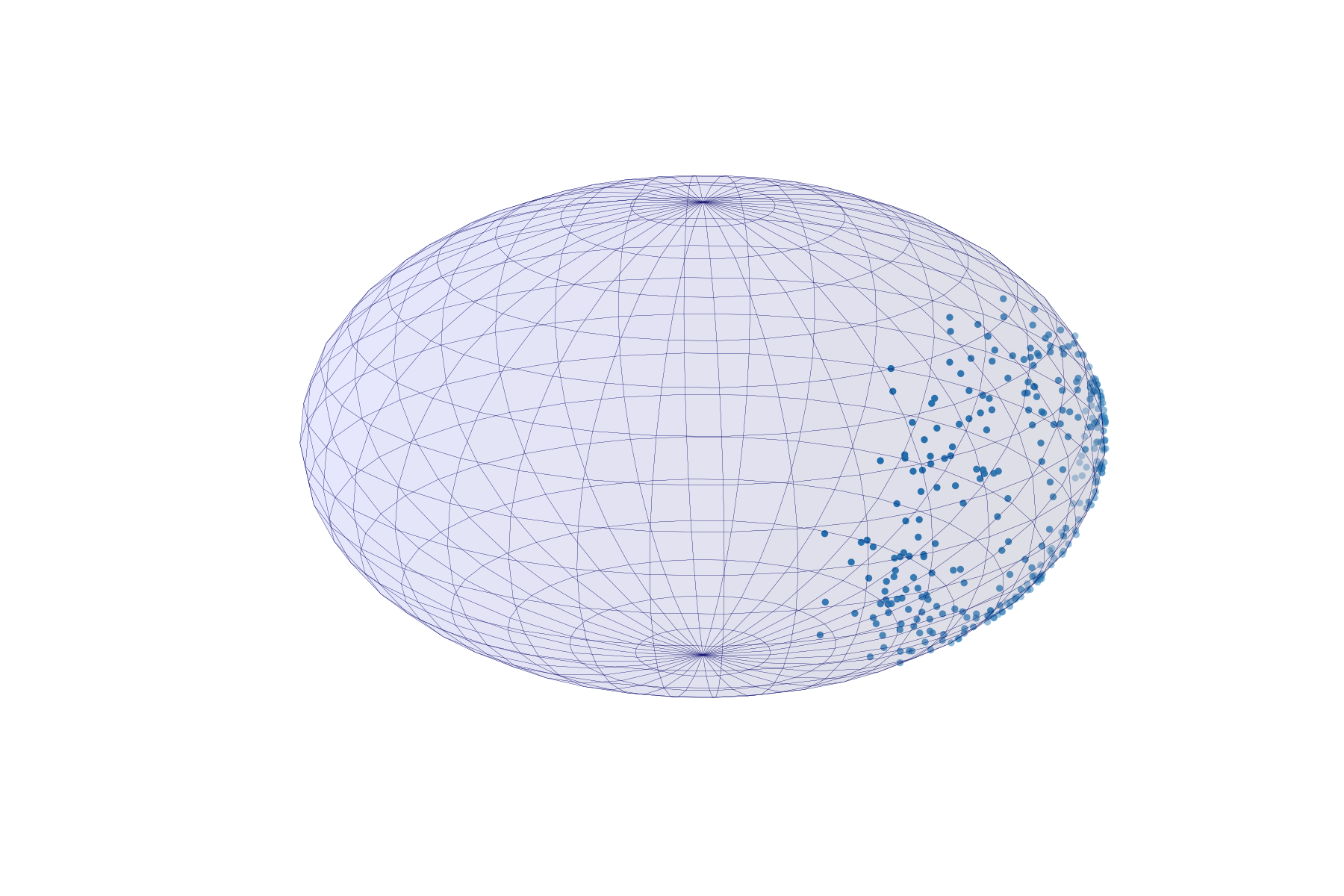
Unique Fréchet mean

and 0-smeary (CLT)

\alpha < 0.56:

Unique Fréchet mean

and 2-smeary

\alpha = 0.56:

Infinitely many means

\alpha > 0.56:

*Stephan Huckemann & Benjamin Eltzner (2018)

\mu

For there exist

such that

t>0

\alpha(t)

Unique likelihood mean

and 0-smeary (CLT)

\alpha < \alpha(t):

Unique likehood mean

and 2-smeary

\alpha = \alpha(t):

Infinitely many means

\alpha > \alpha(t):

\mu

The likelihood means

Summary

(LLN) strong consistency of the likelihood estimator
(CLT) smeariness of the likelihood estimator with Gaussian limit
An example of both 0- and 2-smeariness

We have presented sufficient conditions for

Thank you for your attention!

Law of large numbers

Fix

t>0, \enspace M

\mu

\mu_n

\mu_{n-1}

satisfies (ZC)
satisfies (BPC) if

compact Riemannian manifold,

X: \Omega \to M

E_t \neq \emptyset

(E_{t,n})

Central limit theorem

Fix

t>0, \enspace M

Riemannian manifold,

X: \Omega \to M

Then for any measurable selection is holds that

\sqrt{n}(V_1,...,V_n)^T \overset{\mathcal{D}}{\to} \mathcal{N}(0,\Sigma)

Assume (Uniqueness), (LLN) and (Taylor Expansion)

(\mu_{t,n})

where

x_n = \log_{\mu_t}\mu_{t,n}

V_i = (Rx_n)_i|(Rx_n)_i|^{r-2}

T=diag(T_1,...,T_m)

\Sigma = \frac{1}{r^2}T^{-1}\text{Cov}[\text{grad}_x(-\ln p(x,X,t))|_{x=0}]T^{-1}