Distance
Between
Meshes
by
Hans &
Pernille
Project overview
- Distance on meshes*
- Reproducing Kernel Hilbert Spaces
- Embedding of shapes into space of currents
- Currents metric
- Code (Implementation in Jax)
- Experiments
- Translation, scaling, rotation
- Refinement of mesh
*Stanley Durrleman. Statistical models of currents for measuring the variability of anatomical curves, surfaces and their evolution. Human-Computer Interaction [cs.HC]. Université Nice Sophia Antipolis, 2010. English. fftel-00631382f
Currents metric on shapes
- A solution to the (point)-correspondence issue
- Convergence of 'mesh distance' to the initial continuous representation as the grids become finer
- Works for piecewise smooth curves and surfaces
Let \(\tilde{S}\) be a piecewise smooth curve or surface, and let \(n(x) \) denote the tangent or normal at \(x\in \tilde{S}\).
The shape \(S\) can be characterized by
for test vector fields \( w\in W\).
\( S(w) = \int_S w(x)^t n(x)d\lambda(x) \)
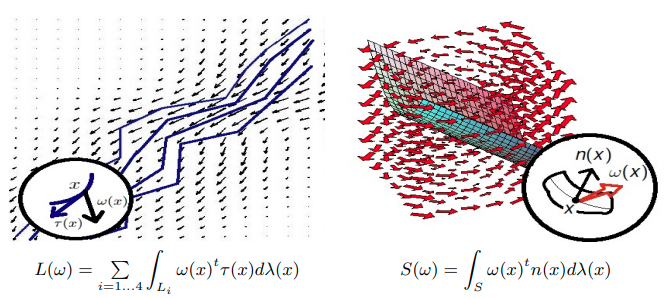
So \(\tilde{S}\) can be identified with \(S \in W^*\) where
\(W^* = \{ f:W\to \mathbb{R} | f \text{ linear and cont.} \} \)
But what is \(W\)?
Reproducing Kernel Hilbert Space
Choose \(W\) as a Reproducing Kernel Hilbert Space with the Gaussian Kernel
This is an infinite dimensional Hilbert space of functions satisfying that \( x\mapsto f(x)\) is cont. for all \(f\in W\).
\( K(x,y) = -\exp(-||x-y||^2) / (2\sigma^2) ) \).
The space has the following important properties:
- W is the closed span of \(K(x,y)\beta\) for points \(y\) and vectors \(\beta\), i.e. \( w = \sum_{i=1}^\infty K(.,y_i)\beta_i\) for all \(w \in W\).
- The inner product on basis vectors is \(\langle K(.,x)\alpha, K(.,y)\beta\rangle_W = \alpha^tK(x,y)\beta \)
Reproducing Kernel Hilbert (dual) Space
By the mapping (contraction) \( L(w)(w') = \langle w,w'\rangle_W \) we can embed \(w\) as \(L(w) \in W^*\). Letting \(\delta_x^\alpha = L(K(.,x)\alpha) \), we may write
\(\tilde{S} \sim S = \sum_i\delta_{x_i}^{\alpha_i}\)
The inner product on \(W\) descents to one on \(W^*\) by
\(\langle \delta_{x}^\alpha, \delta_y^\beta \rangle_{W^*} = \langle K(.,x)\alpha, K(.,y)\beta \rangle = \alpha^tK(x,y)\beta \)
We say that \( W^*\) is the space of currents, which represents our shapes.
\( \langle \sum_i \delta^{\alpha_i}_{x_i},\sum_i \delta^{\beta_i}_{y_i}\rangle_{W^*} = \sum_i \alpha_i^tK(x_i,y_i)\beta_i \)
Distance of shapes
The Currents metric of two shapes is
\( d(S,S') = || S-S' ||_{W^*} = (\langle S-S', S-S' \rangle)^{1/2} \)
If \(S = \sum_i \delta^{\alpha_i}_{x_i} \) and \(S' = \sum_i \delta_{y_i}^{\beta_i} \) then
\( d(S,S') = \sum_{i,j} \alpha_i^t K(x_i,x_j) \alpha_j + \sum_{i,j} \beta_i^tK(y_i,y_j) \beta_j \)
\( -2 \sum_{i,j} \alpha_i^tK(x_i,y_i)\beta_j \)
\(\sum_{i,j} X_i^tK(a_i,b_j) Y_j = X^T Y * K \)
where \(K\) is the matrix \(K_{ij} = K(a_i,b_j) \).
The inner product can be written as the matrix multiplication
Influence of kernel
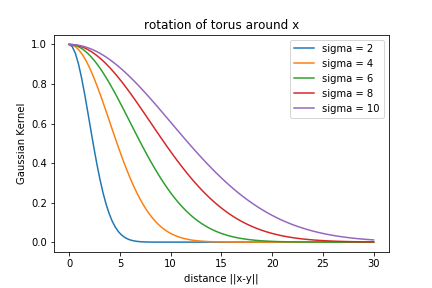
\( K(x,y) = -\exp(-||x-y||^2) / (2\sigma^2) ) \).
Gaussian Kernel:
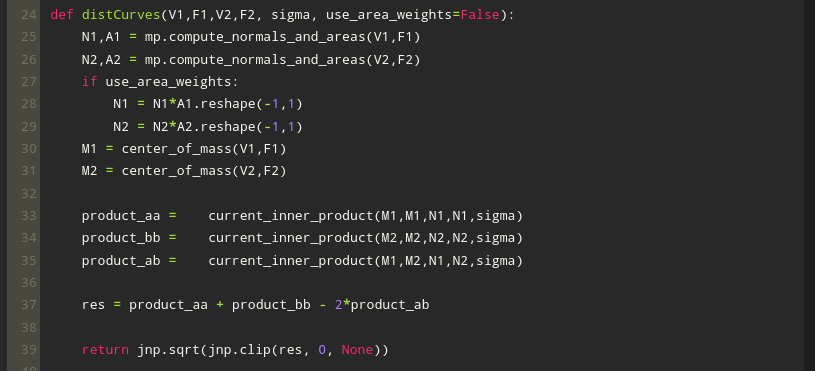
The Code


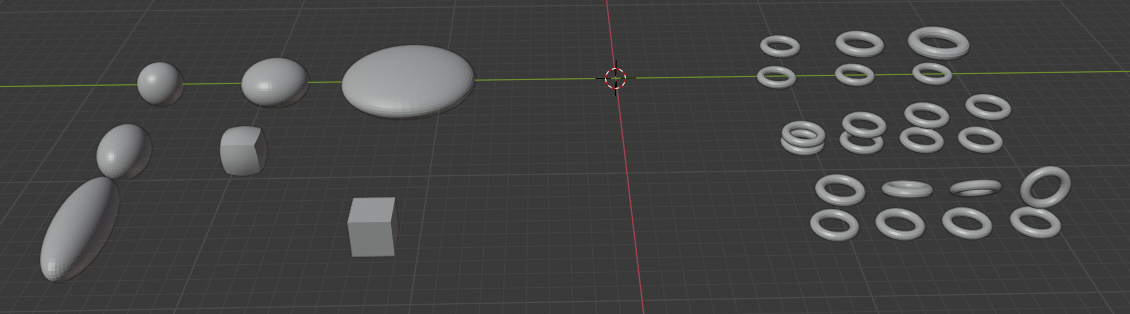
The Meshes
Experiments
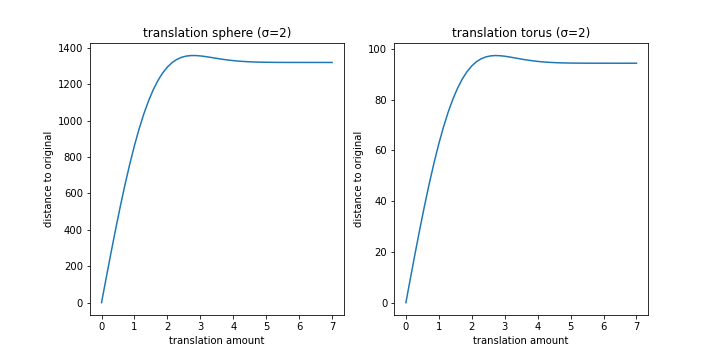
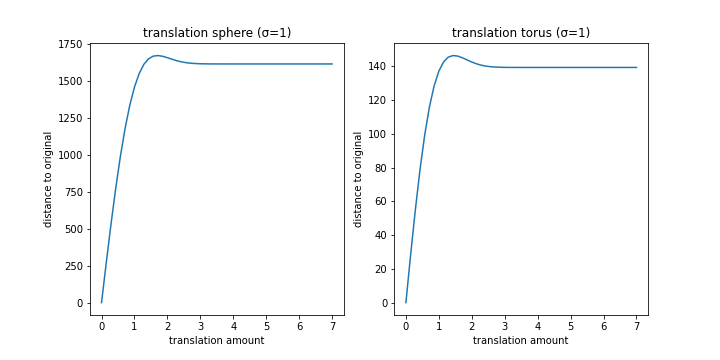
Translation
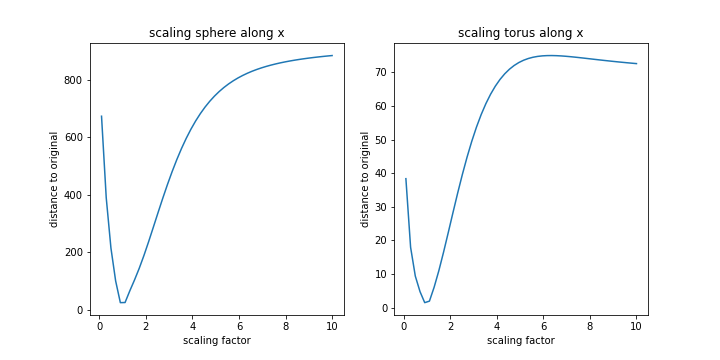
Scaling
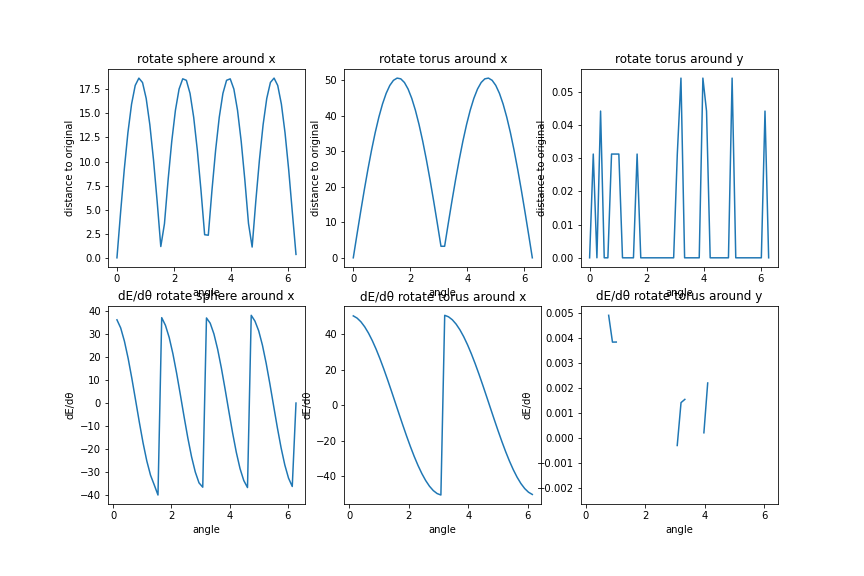
Rotation

Sphere from cube
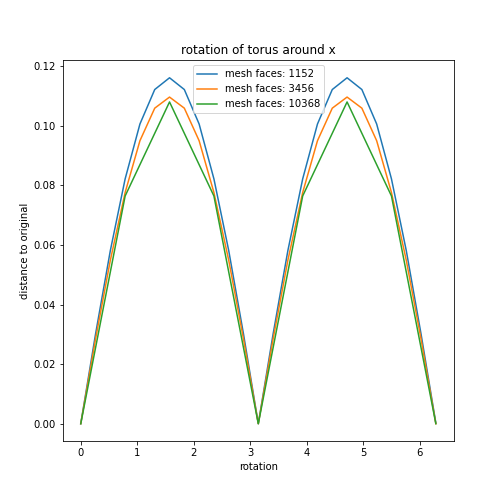
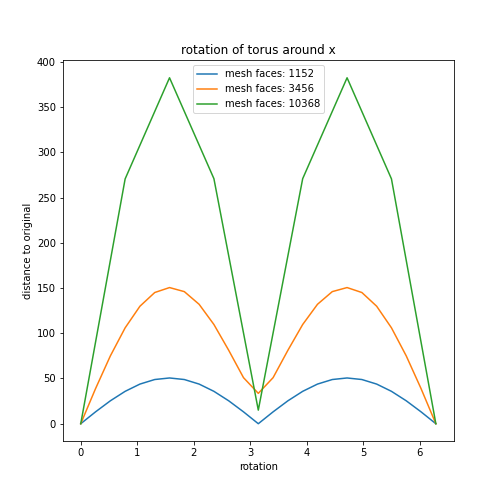
Mesh refinement
Normalizing with area weights
Our Questions
- Should the normals be scaled by area weights?
- What are good use cases?
- What \(\sigma\)-values are appropriate?