K-Funktioner på Fibre
Forskning i Data Science
Pernille Hansen
Lidt om mig
- Pernille Hansen
- Bachelor og kandidat i matematik fra KU
- Ph.d.-studerende på datalogisk institut i IMAGE sektionen
Forskning
- Statistisk på former istedet for punkter
- Definere nye statistiske værktøjer og analysere deres egenskaber og mulighed for anvendelse
- Middelværdi for former og K-funktioner for punkt processer


Punkt processer
En punkt process er en stokastisk variabel der ved hvert udfald giver en mængde af punkter.
Vi analyserer punkt processer via statistiske værktøjer som f.eks. K-funktioner.
og er defineret ved
\(K(r)\) = gennemsnitlige antal punkter inden for radius \(r\)
Ripley’s K-funktion er et værktøj til at afgøre om punkterne
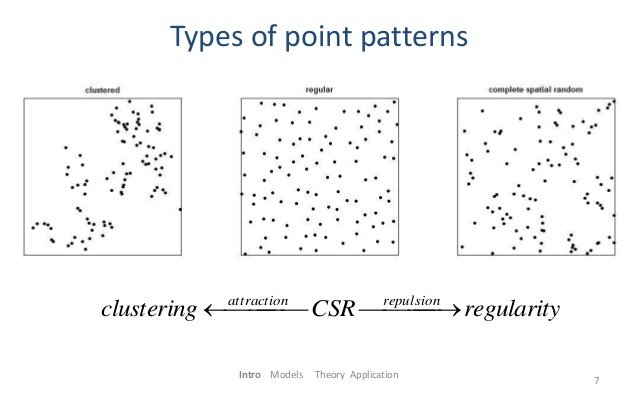
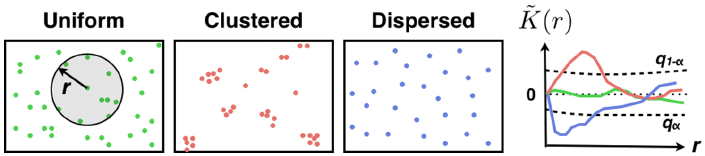
1) er helt tilfældigt fordelt (Uniform)
2) samler sig i grupper (Clustered)
3) spreder sig (Dispersed)
Ripley's K-funktion
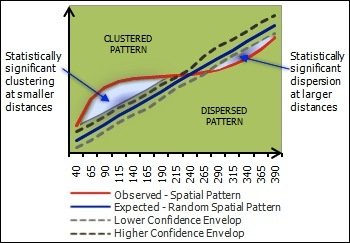
Sammenligning med K-funktionen for en uniform fordeling \( K_U \)
- \(K(r) < K_U(r) \): Indikation for spredning ved radius \(r \).
- \(K(r) \simeq K_U(r) \): Uniform fordelt data
- \(K(r) > K_U(r) \): Indikation for gruppering ved radius \(r \).
Ripley's K-funktion
\(r\)
\( K(r)\)

Forskningsprojekt
Definere en K-funktion for processer hvor hvert udfuld er en mængde af former, f.eks. fibre i 3d.
Problemstillinger
- Afstandsmål mellem fibre
- Uniform fiber process
- Meningsfuldt statistisk værktøj
Afstandsmål
Afstandsmål:
\( d(\gamma_1,\gamma_2) = \Big( \int_{\gamma_1-\gamma_2}\int_{\gamma_1-\gamma_2} \tau_{\gamma_1-\gamma_2}(x)^tK(x,y) \tau_{\gamma_1-\gamma_2}(x) d\lambda(x)\lambda(y) \Big)^{1/2} \)

For punkter i planen har vi aftandsmålet
\(d(x,y) = ||x-y|| = \sqrt{(x_1-y_1)^2+(x_2-y_2)^2} \)
Hvordan oversættes det til fibre?
Her bliver min matematiske baggrund nyttig!
K-funktion for en fiber process \(X\) observeret i et vindue \( W\) is
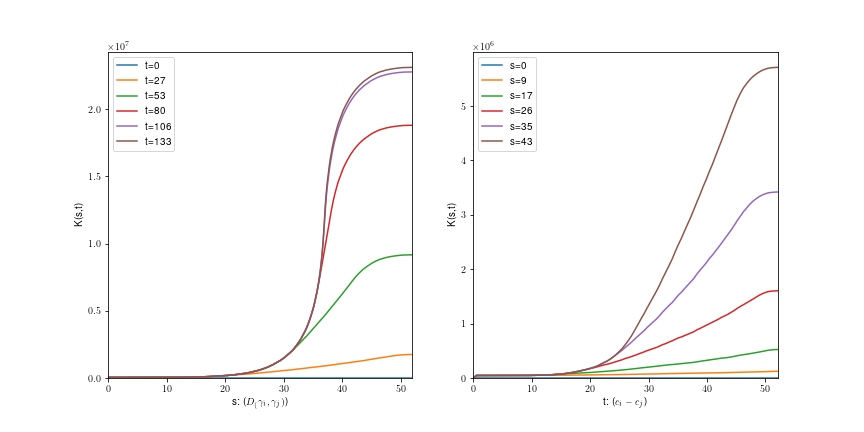
K-funktionen
- \( s \) form parameter
- \(t\) afstand parameter
\( K(s,t) = \frac{1}{|W|\nu(S_0)} \sum \sum 1[||c(\gamma)-c(\gamma')|| \leq t, d_c(\gamma,\gamma')\leq s]\)
\( \gamma\in X:c(\gamma)\in W\)
\( \gamma' \neq \gamma \in X \)
\( =\) forventet antal fibre hvor midtpunkter er tættere end \(t \) og fiberafstand er mindre end \(s\)
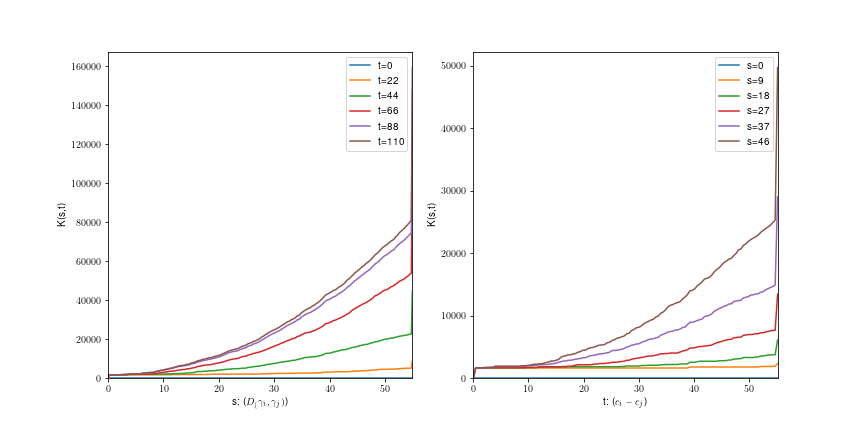
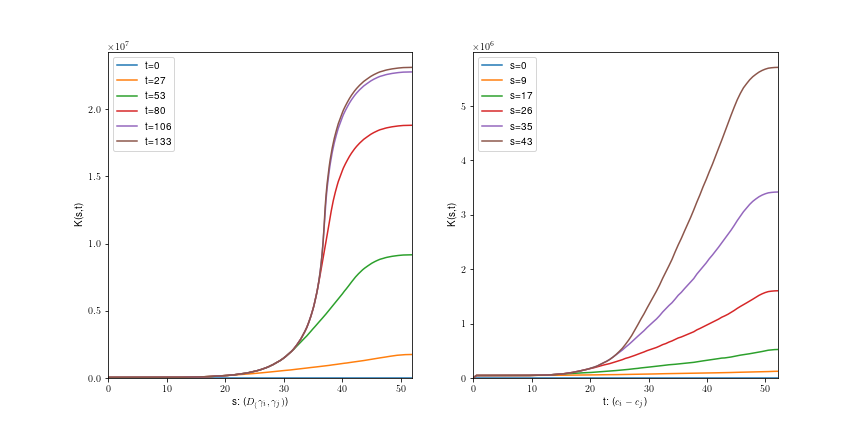
Uniform fiber process
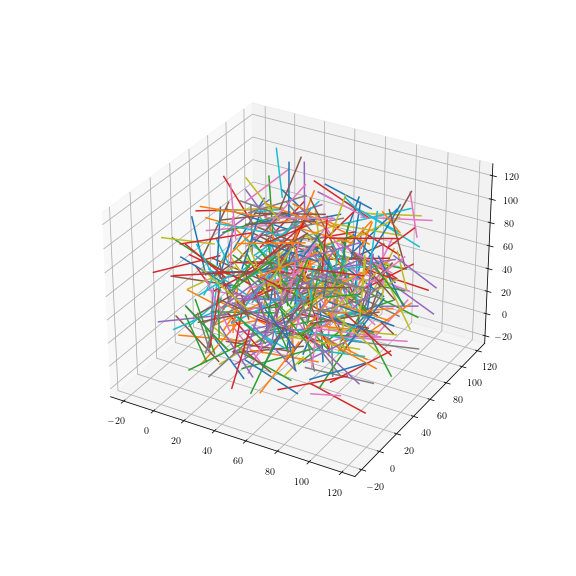
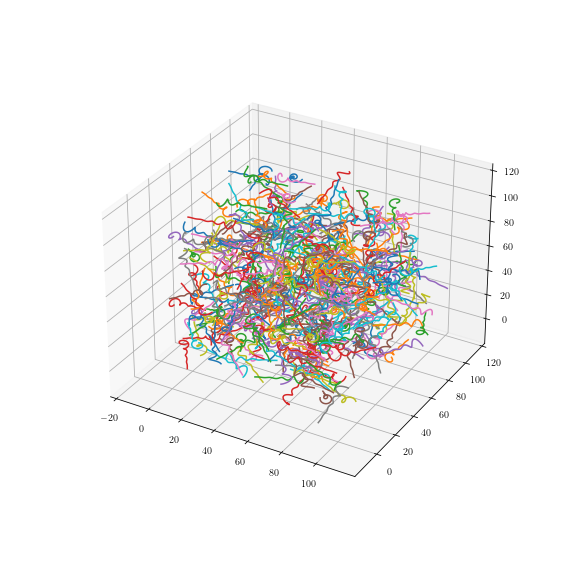
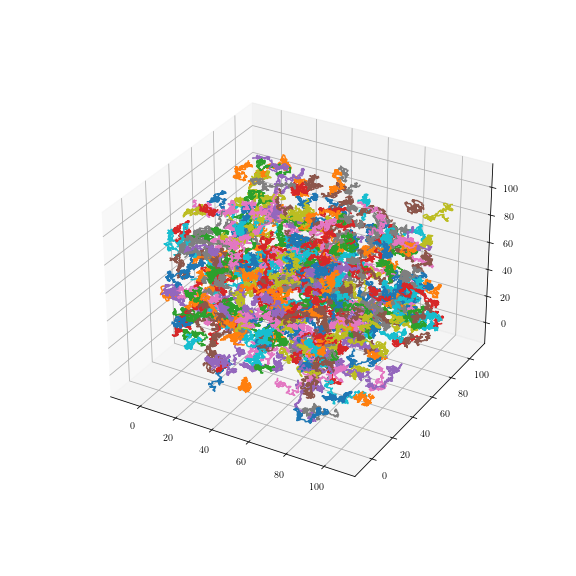
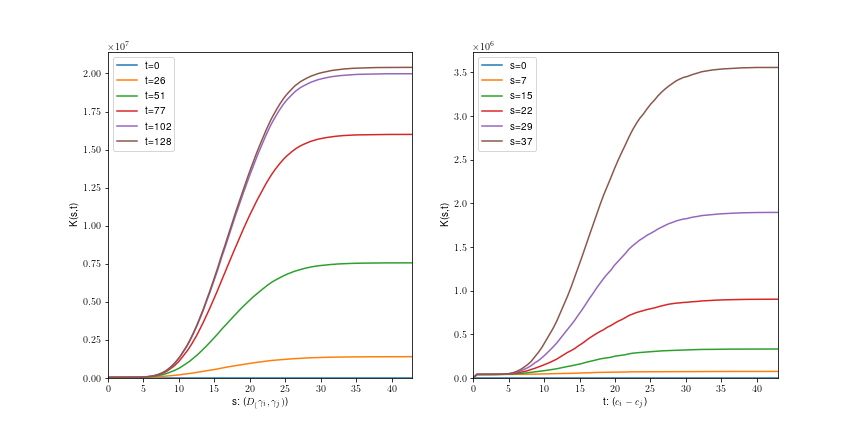
Tilfældigt
roterede linjer:
Tilfældige stier:
Tilfældigt
roterede spiraler:
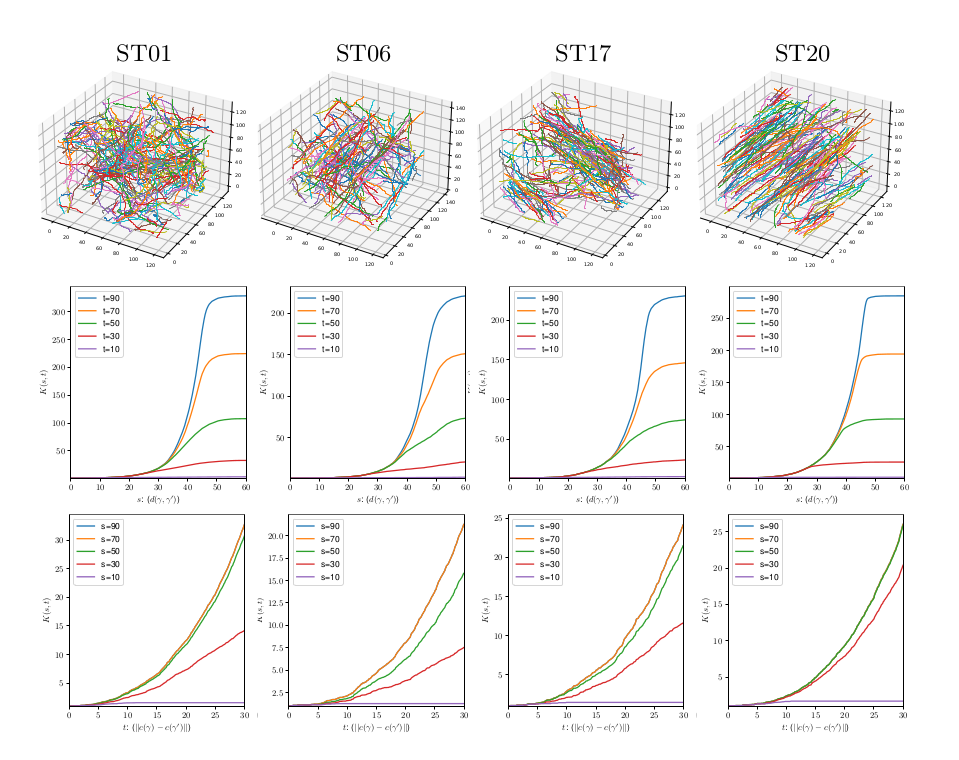
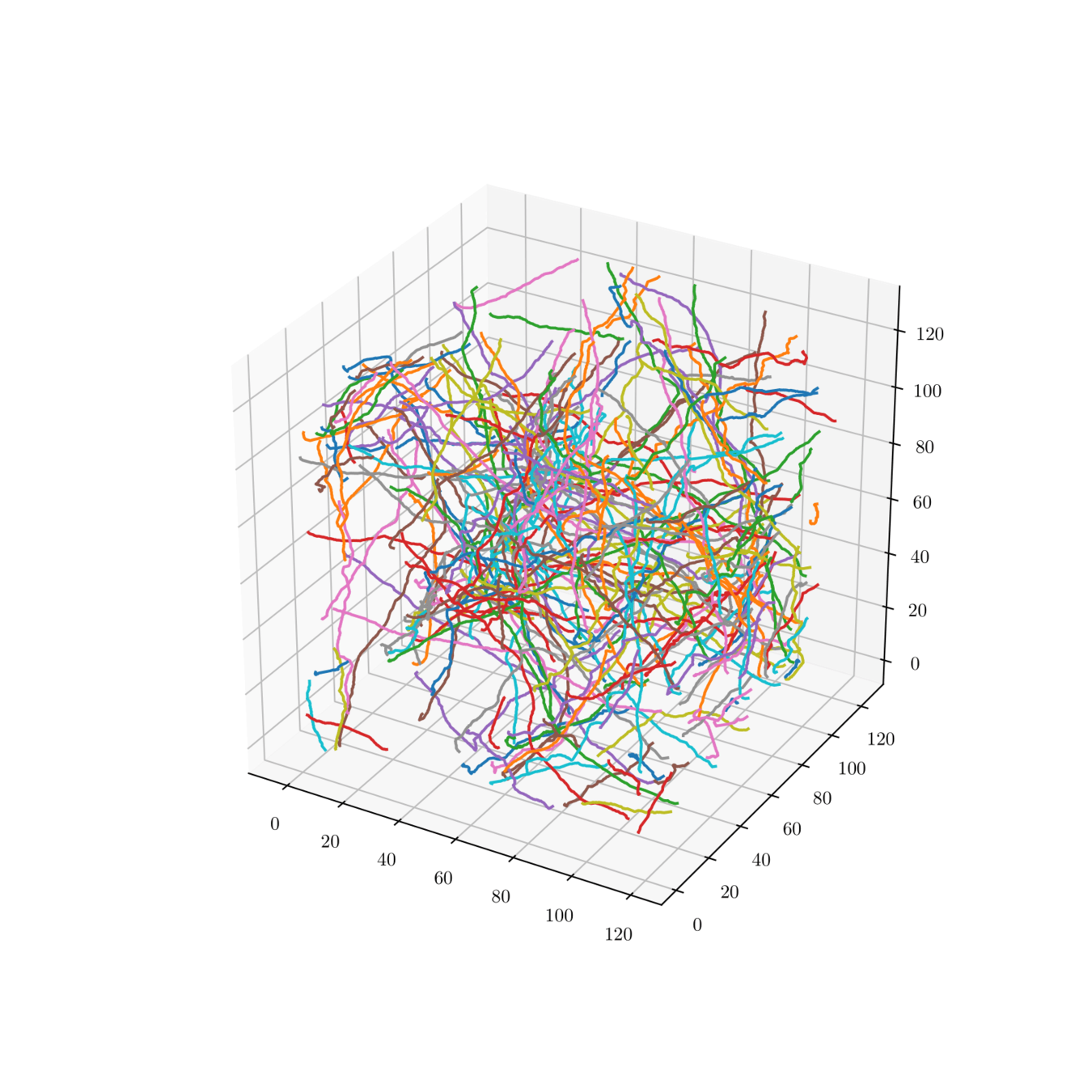
Myelin fibers
Forskning i Data Science
- Anvendeligt i den virkelige verden
- Teoretisk fundament fra matematik
- Spændende datasæt

Tak for jeres opmærksomhed!
