Middelværdier på mangfoldigheder

Pernille E.H. Hansen

University of Copenhagen

Indhold

Motivation
Statistik på mangfoldigheder
Fréchet middelværdien
Diffusionsmiddelværdien

Middelværdi på $ \mathbb{R}^n $

Y_1,...,Y_N\overset{\text{iid}}{\sim} Y

\mu = \mathbb{E}[Y]

\rightarrow \mu_N=\frac1N\sum_{i=1}^NY_i

Eksisterer entydigt hvis $\mathbb{E}[|Y|]<\infty $
Store tals lov $$ \mu_N \overset{a.s.}{\to} \mu$$
Den centrale grænseværdisætning $$\sqrt{N}(\mu_N-\mu) \to \mathcal{N}(0,\Sigma)$$

\frac{1}{N} \sum_{i=1}^N X_i, \enspace\mathbb{E}[X]

$X_1 ,...,X_N\overset{\text{iid}}{\sim} X \in M \rightarrow $

$ Y :\Omega \to \mathbb{R}^n\rightarrow $

Ikke lineære rum?

Mål:

Udvikle statistiske begreber og metoder for ikke lineært data
Beskrive deres opførsel (eksistens, entydighed, konsistens, osv.)

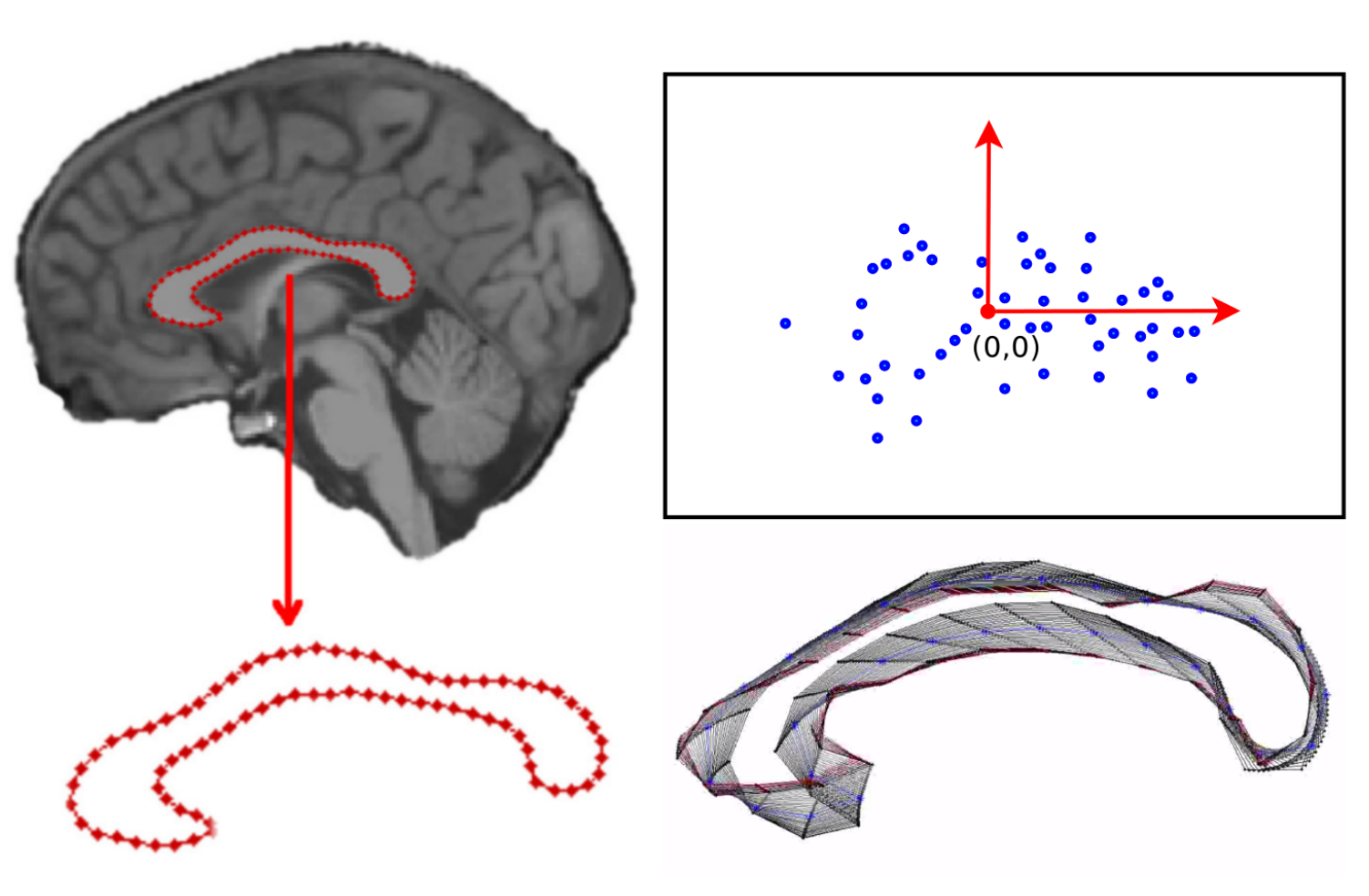
Medicinsk billedanalyse

Alzheimer's Ændringer i
Corpus Callosum (CC)

Hypotese: (AD) kan blive opdaget fra form på (CC).

Mangfoldigheder

En topologisk mangfoldighed $M$ af dimension $ n$ er et topologisk rum der opfylder

$ M$ er Hausdorff
$ M $ er 2. countable
$ M $ er lokalt homeomorf til $ \mathbb{R}^n$

En glat mangfoldighed er udstryret med et atlas $ (U_\alpha,\varphi_\alpha )$ med glatte transitions afbildninger.

\varphi_\alpha

\varphi_\beta

U_\alpha

U_\beta

\mathbb{R}^n

Mangfoldigheder

Til ethvert punkt $ x\in M $ findes et tangetrum $T_xM\cong \mathbb{R}^n $.

En Riemannsk metrik er en samling af indre produkter $\langle v,w\rangle_x $ hvor

$$ x \mapsto \langle v,w \rangle_x$$

er glat for alle $ v,w\in T_xM $

Den nedarvede metrik på $ M $ er da

$$ dist(x,y) = \inf \{ L(\gamma) | \gamma(0)=x,\gamma(1)=y \} $$

Længden af en kurve $ \gamma:[0,1] \to M $$$L(\gamma) = \int^1_0 || \gamma'(t) ||_{\gamma(t)}dt$$

Geodæter er lokalt længdeminimerende kurver.

Mangfoldigheder

For sandsynlighedsrum $ (\Omega, \mathcal{B}, P) $ kan vi betragte stokastiske variabel $ X: \Omega \to M $

Afbildningen $p_X: M\to [0,1] $ er en tæthed for $ X$ mht. volumemålet $ dM$ hvis

$$ P(x\in B) = \int_B p_X(y) d M(y)$$

for alle $ B\in \mathcal{B}(M) $.

For $ f:M \to \mathbb{R}^n $ er $f(X):\Omega \to \mathbb{R}^n$ er reel stok. variabel, med middelværdi

$$ \mathbb{E}[f(X)] = \int f(y) p_X(y) dM(y)$$

Mangfoldigheder

Fréchet middelværdien

Middelværdien $ \mathbb{E}[X] $ af $ X: \Omega \to \mathbb{R}^n $ opfylder

= \arg\min_{y\in \mathbb{R}} \int dist(x,y)^2 dP_X(x)

\mathbb{E}[X] = \arg\min_{y\in \mathbb{R}} Var(X,y)

Definition:

E = \arg\min_{y\in\mathcal{M}} \mathbb{E}[\text{dist}(y,X)^2]

Det Riemannske center af en stok. variabel $ X:\Omega \to M$ er

Hvis $ M = \{ \mu \} $, siger vi at $ \mu$ er Fréchet middelværdien af $ X $.

Eksistens og entydighed

Eksistens er ikke garanteret
Entydighed er bestemt heller ikke!

Sætning [Karcher & Kendall]

Der eksisterer en entydig Karcher middelværdi i $ B = B(y,r) \subset M$, hvis $ X:\Omega \to M $ kun har masse i $ B$ og B opfylder:

Entydige geodæter
Begrænset krumning og radius

Estimator

For $ X_1,...,X_N\overset{\text{iid}}{\sim} X$ defineres den empiriske Fréchet funktionen

$$ F_N(y) = \frac{1}{N} \sum_{i=1}^N dist(y,X_i)^2$$

og dermed de empiriske Fréchet middelværdier

$$ E_N = \arg\min_{y\in M} F_N(y) $$

Den generaliserede centrale grænseværdisætning

På $ \mathbb{R}^m $

\sqrt{n}\mu_N \overset{\mathcal{D}}{\to} \mathcal{N}(\mu,\Sigma)

smeary:

n^{\frac{1}{2(k+1)}}X_N \overset{\mathcal{D}}{\to} \mathscr{L}

CLT $ \Rightarrow$ 0-smeary

CLT:

For $ X_1,...,X_N\overset{iid}{\sim} X $ på $ \mathbb{R}^m $ med $ \mathbb{E}[X] = \mu $ og $ \mu_N = \frac{1}{N} \sum_{i=1}^N X_i $

På en Riemannsk mangfoldighed $ M $

smeary

(Y_n)

\phi

X_n

\Leftrightarrow

smeary

*Stephan Huckemann & Benjamin Eltzner (2018)

For $Y_1,...Y_N \overset{iid}{\sim} Y $ på $M $ og $\phi: U\to \mathbb{R}^{m} $ kort med $ \mu \in U $ definerer vi $$ X_n = \phi(Y_n) - \phi(\mu) \in \mathbb{R}^m $$

Eksisterer der $ k\geq 0 $ så $ M_N $ er $ k $-smeary?

(Entydighed):
(Konvergens):
(Taylorrække): Der eksisterer

M = \{\mu\}

\mu_{n}\overset{\mathbb{P}}{\to}\mu, \text{ for } \mu_n\in E_n

F(\phi(x)) = F(\phi(\mu)) + \sum_{i=1}^m T_i |(Rx)_i|^r + o(||x||^r)

\geq 2, R\in\text{SO}(m), T_1,...,T_m\neq 0 \text{ så}

For $ X: \Omega \to M $, antag

\mu_n

smeary

med

k = \quad-2

\mathscr{L} \sim \mathcal{N}

På en Riemannsk mangfoldighed $ M $

The Fréchet means

Entydig Fréchet m. $ \mu $

og 0-smeary (CLT)

\alpha < 0.56:

Entydig Fréchet m. $ \mu $

og 2-smeary

\alpha \simeq 0.56:

Uendeligt mange m.

\alpha > 0.56:

*Stephan Huckemann & Benjamin Eltzner (2018)

\mu

P(X = \mu) = 1-\alpha

P(X\in \mathbb{L}) = \alpha

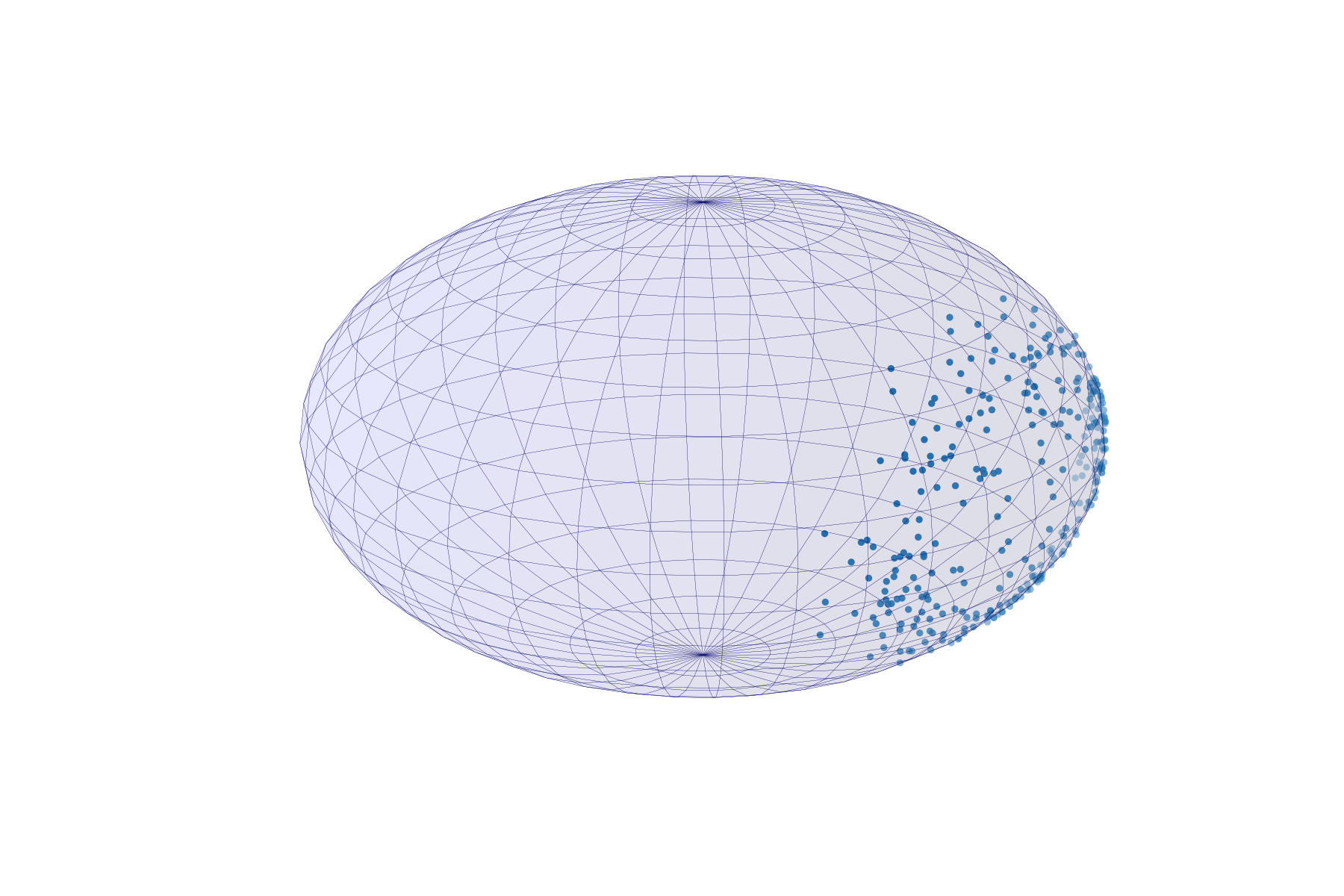
under polskifte

Magnetiske nordpolspositioner

Hvorfor opstår smearieness?

Masse på cut locus?
- Modeksempel på 5-sfæren
Krumningen?
Topologien?

Mange definitioner af smearieness:

Topologisk, geometrisk, "finite sample"

Diffusions-middelværdier

Varmelednings-funktionen

(\partial_t-\Delta_x)p(x,y,t) = 0

\lim_{t\to 0} p(x,y,t)= \delta_x(y)

En funktion $$ p:M \times M \times (0,\infty) \to (0,\infty) $$ er en varmeledningsfunktion på $ M$ hvis den opfylder

p \in \mathcal{C}^\infty(M\times M\times \mathbb{R}_+)

t = 0.5

t = 0.1

Begrænsninger

1) Eksistens

Stochastisk komplet
$M$ kompakt

2) Lukket form

Euclidiske rum
Sfærerne
Hyperbolske rum

Brownian motion på mangfoldigheder

p(x,y,t) \approx \text{ "sandsynlighed"}

\text{for at ramme }y \text{ til tid }t\text{ med start i }x

B_t = y

For $ X_1,...,X_N \overset{iid}{\sim} X \in M $

$$ \mu = \arg\max_{y\in M} \frac{1}{N} \ln(p(y,X_i,t))$$

mest sandsynlighed start af $ (B_t)$

\mu = \arg\min \mathbb{E}_X[-\ln p(x,X,t)]

En Brownian motion på $ M $ er en Markov process $ (B_t )$ med tæthed $ p(x,y,t) $

Diffusions $t$-middelværdier

Fix $t>0$. Diffusions $t$-middelværdier $E_t(X)$ af en stoc. variabel $X: \Omega \to M$ er de værdier der minimerer log-likelihood funktionen,

$$ L_t(y) = \mathbb{E}[-\ln(p(y,X,t)]$$

Altså,

$$ E_t(X) = \arg\min_{y\in M} \mathbb{E}[-\ln(p(y,X,t)]$$

På $\mathbb{R}^m$?

Varmeledningsfunktionen på $\mathbb{R}^n$ for ethvert $t>0$ er

p(x,y,t) =\frac{1}{(4\pi t)^{m/2}} e^{\frac{-\text{dist}_{\mathbb{R}^m}(x,y)^2}{4t}}

E_t(X)=\arg\min_{y\in \mathbb{R}^m} \int_{\mathbb{R}^m} \frac{2}{m}\ln(4\pi t) - \left(\frac{\text{dist}_{\mathbb{R}^m}(x,y)^2}{4t}\right)d\mathbb{P}_X(x)

= \arg\min_{y\in \mathbb{R}^m} \int_{\R^m} \text{dist}_{\mathbb{R}^m}(x,y)^2 d\mathbb{P}_X(x) = \mathbb{E}[X]

For $ X:\Omega \to \mathbb{R}^m $, har vi

Sfærerne

p(x,y,t) = \sum_{l=0}^\infty e^{-l(l+m-1)\sqrt{2t}}\frac{2l+m-1}{m-1} \frac{1}{A_{\mathcal{S}}^{m}} C_l^{(m-1)/2}(\langle x,y\rangle_ {\R^m} )

Betragt $X: \Omega \to \mathcal{S}^m $:

For $m\geq 2$, $t>0$ og $\alpha\in [0,1/2]$, hvad er diffusions $t$-middelværdierne?

\mu

-\mu

P(X = -\mu) = \alpha

P(X = \mu) = 1-\alpha

Varmeledningsfunktionen på $\mathcal{S}^m$ for $ m\geq 2$ og $t>0$ er

\mu

-\mu

P(X = \mu) = 1-\alpha

P(X = -\mu) = \alpha

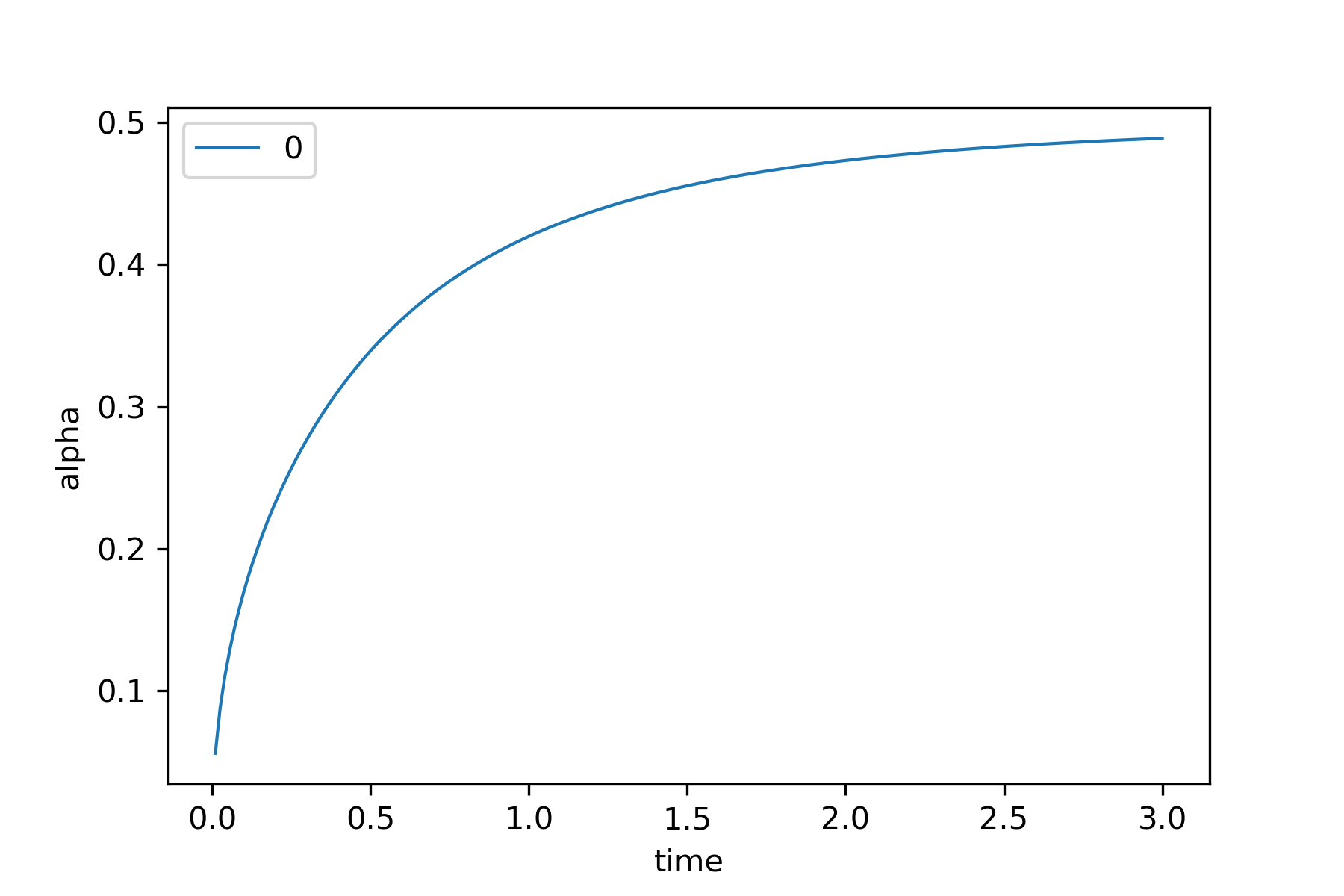
For $m\geq 2$ og $t>\Lambda_{t,m}$ hvor

eksisterer $\alpha_m(t)$ så

Fréchet middelværdierne

$\alpha = 0$: Entydig
$ \alpha>0$: Uendelig mange

Diffusion $t$-middelværdierne

$ \alpha \leq \alpha_m(t) $: Entydig diffusions $t$-middelværdi
$ \alpha > \alpha_m(t)$ : Uendeligt mange

Derudover, $\alpha_{m}(t) \to 1/2$ når $t\to \infty$

\Lambda_{t,m} = \frac12 \left(\log\left( \frac{8(m+3)}{(m+1)} \right) \frac12 \right)^2 \leq 0.838

Estimator

For $ X_1,...,X_N\overset{\text{iid}}{\sim} X$ defineres den empiriske Diffusions $t$-funktion

$$ L_{t,N}(y) = \frac{1}{N} \sum_{i=1}^N -\ln(p(y,X_i,t))$$

og dermed de empiriske Diffusions $t$-middelværdier

$$ E_{t,N} = \arg\min_{y\in M} L_{t,N}(y) $$

Tilstrækkelige betingelser fra Fréchet estimatoren medfører også at $ E_{t,N} $ er en konsistent estimator!

(Entydighed):
(Konvergens):
(Taylorrække): Der eksisterer

E_{t} = \{ \mu_t \}

\mu_{t,n}\overset{\mathbb{P}}{\to}\mu_t

L_t(\phi(x)) = L_t(\phi(\mu)) + \sum_{i=1}^m T_i |(Rx)_i|^r + o(||x||^r)

\geq 2, R\in\text{SO}(m), T_1,...,T_m\neq 0 \text{ så}

For $t>0$ og $ X: \Omega \to M $, antag

E_{t,N}

smeary

med

k = \quad-2

\mathscr{L} \sim \mathcal{N}

\mu

-\mu

P(X = \mu) = 1-\alpha

P(X = -\mu) = \alpha

For $m\geq 2$ og $t>\Lambda_{t,m}$ hvor

eksisterer $\alpha_m(t)$ så

Diffusion $t$-middelværdierne

$ \alpha \leq \alpha_m(t) $: Entydig diffusions $t$-middelværdi
$ \alpha > \alpha_m(t)$ : Uendeligt mange

\Lambda_{t,m} = \frac12 \left(\log\left( \frac{8(m+3)}{(m+1)} \right) \frac12 \right)^2 \leq 0.838

$ \alpha < \alpha_m(t) $: 0-smeariness
$ \alpha = \alpha_m(t)$ : 2-smearieness

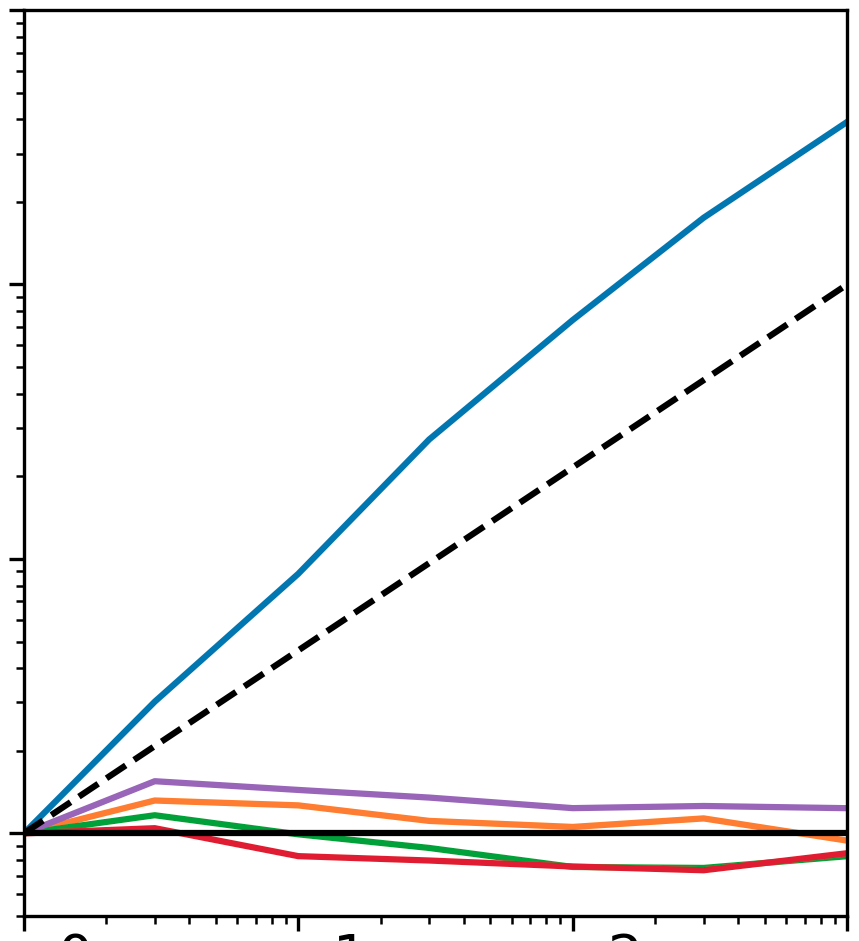
under polskifte

Magnetiske nordpolspositioner

Middelværdier på mangfoldigheder

Indhold

Middelværdi på \( \mathbb{R}^n \)

Ikke lineære rum?

Medicinsk billedanalyse

Mangfoldigheder

Mangfoldigheder

Mangfoldigheder

Mangfoldigheder

Fréchet middelværdien

Eksistens og entydighed

Estimator

Den generaliserede centrale grænseværdisætning

På \( \mathbb{R}^m \)

smeary:

CLT:

På en Riemannsk mangfoldighed \( M \)

smeary

smeary

På en Riemannsk mangfoldighed \( M \)

The Fréchet means

Hvorfor opstår smearieness?

Diffusions-middelværdier

Varmelednings-funktionen

Brownian motion på mangfoldigheder

Diffusions \(t\)-middelværdier

På \(\mathbb{R}^m\)?

Sfærerne

Fréchet middelværdierne

Diffusion \(t\)-middelværdierne

Estimator

Diffusion \(t\)-middelværdierne

Tak for jeres opmærksomed!