Shape transformations on manifolds

by Pernille Hansen
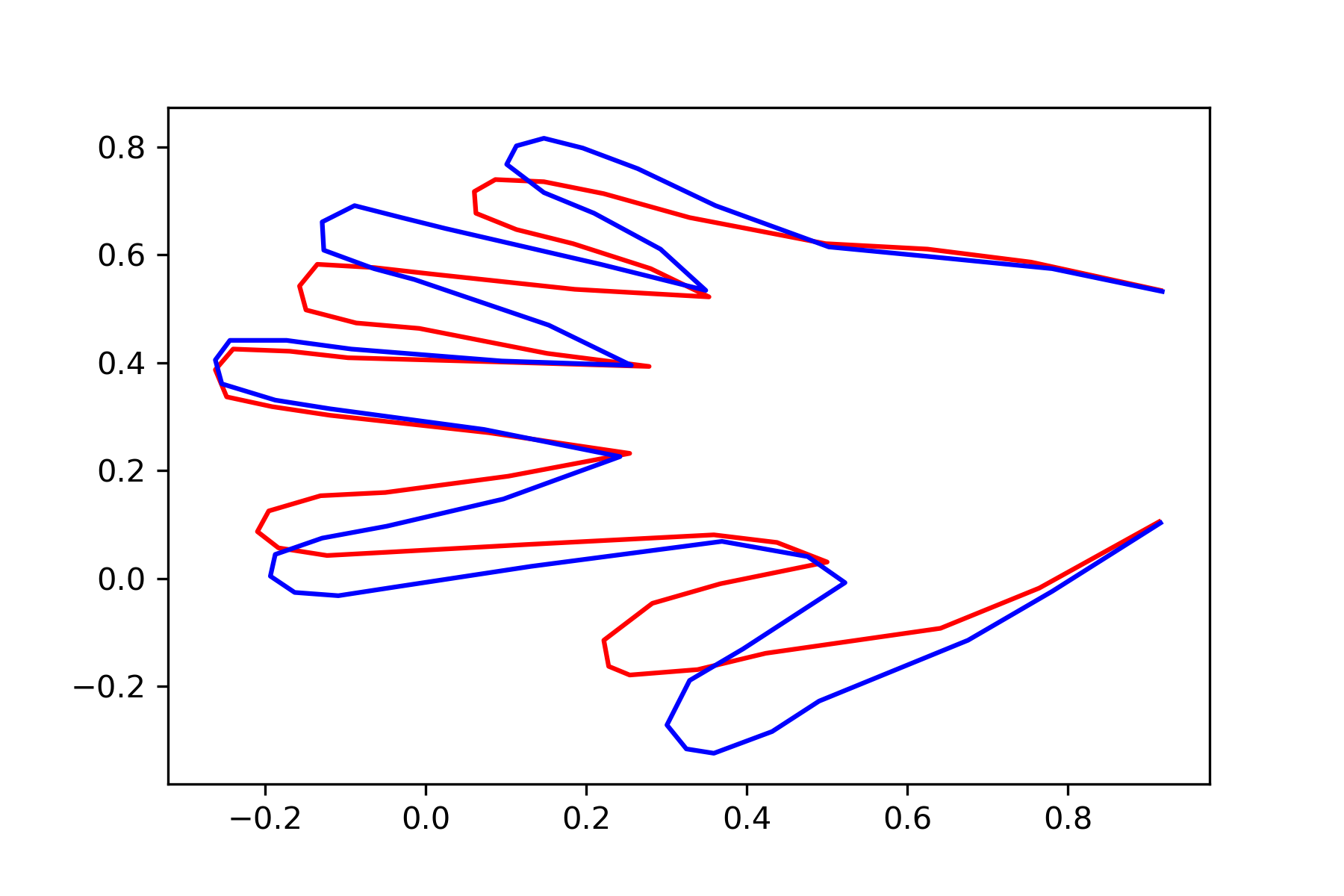
Affine transformation
Find matrix \(A\) such that
- \(AH_1 = A_2\)
- \( ||H_2 - AH_1||_2 \) is minimized
.. Can we do this for manifold-
valued data?
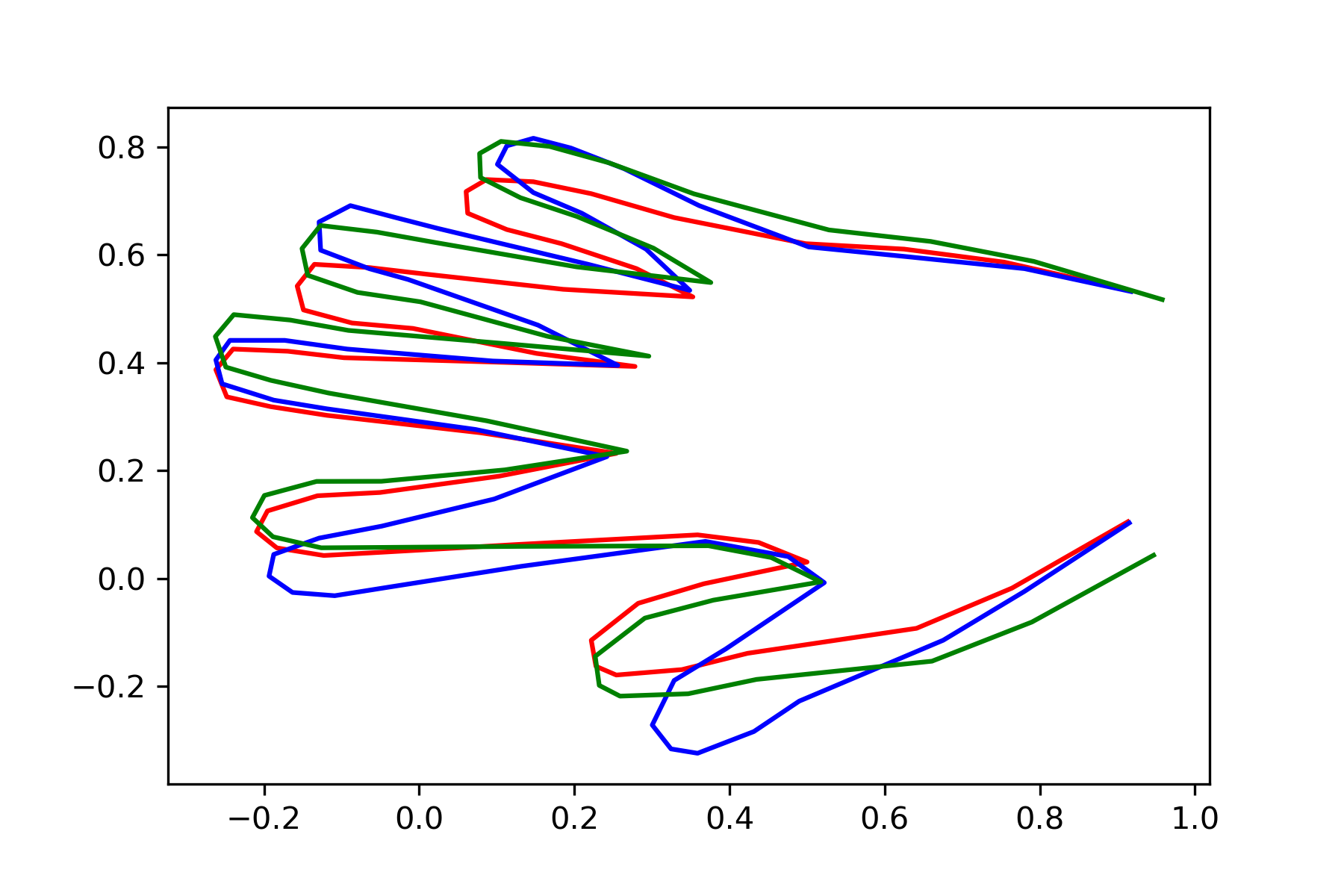
Hand 1 \(H_1\), Hand 2 \(H_2\)


Manifolds
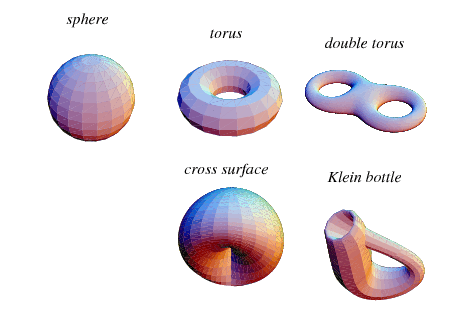
For every \( x\in M \):
- \( log_x : M \to T_x M\)
- \( exp_x : T_x M \to M \)

The 2-Sphere
\( exp_x\)

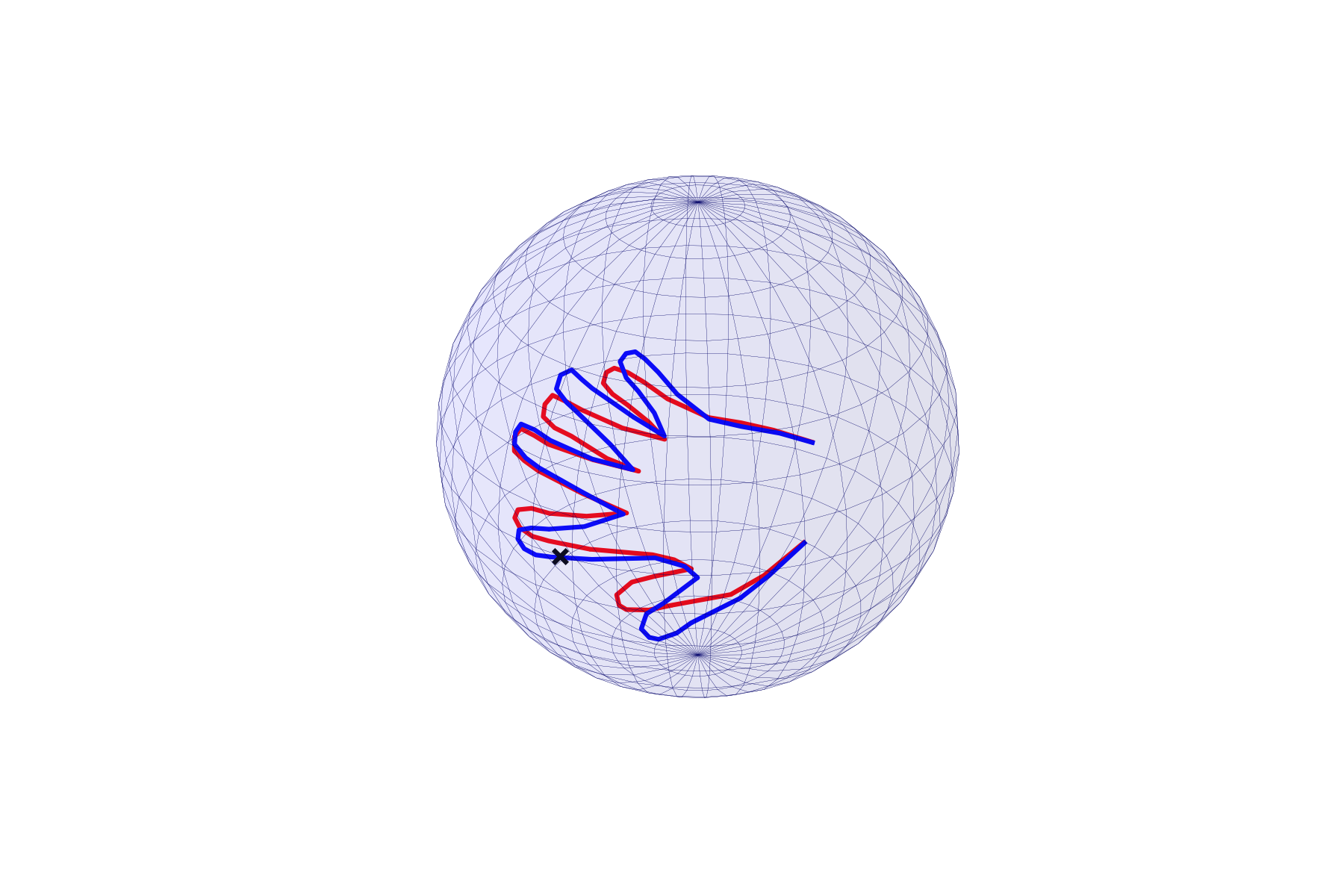
Pick \( x_0 = (0,-1,0) \)
\( exp_{x_0}\)
\( exp_{x_0}\)

Q: Does the solution depend on \(x\)?
Hand 1 \(H_1\)
Hand 2 \(H_2\)
Compute \(A_{x_0} \)
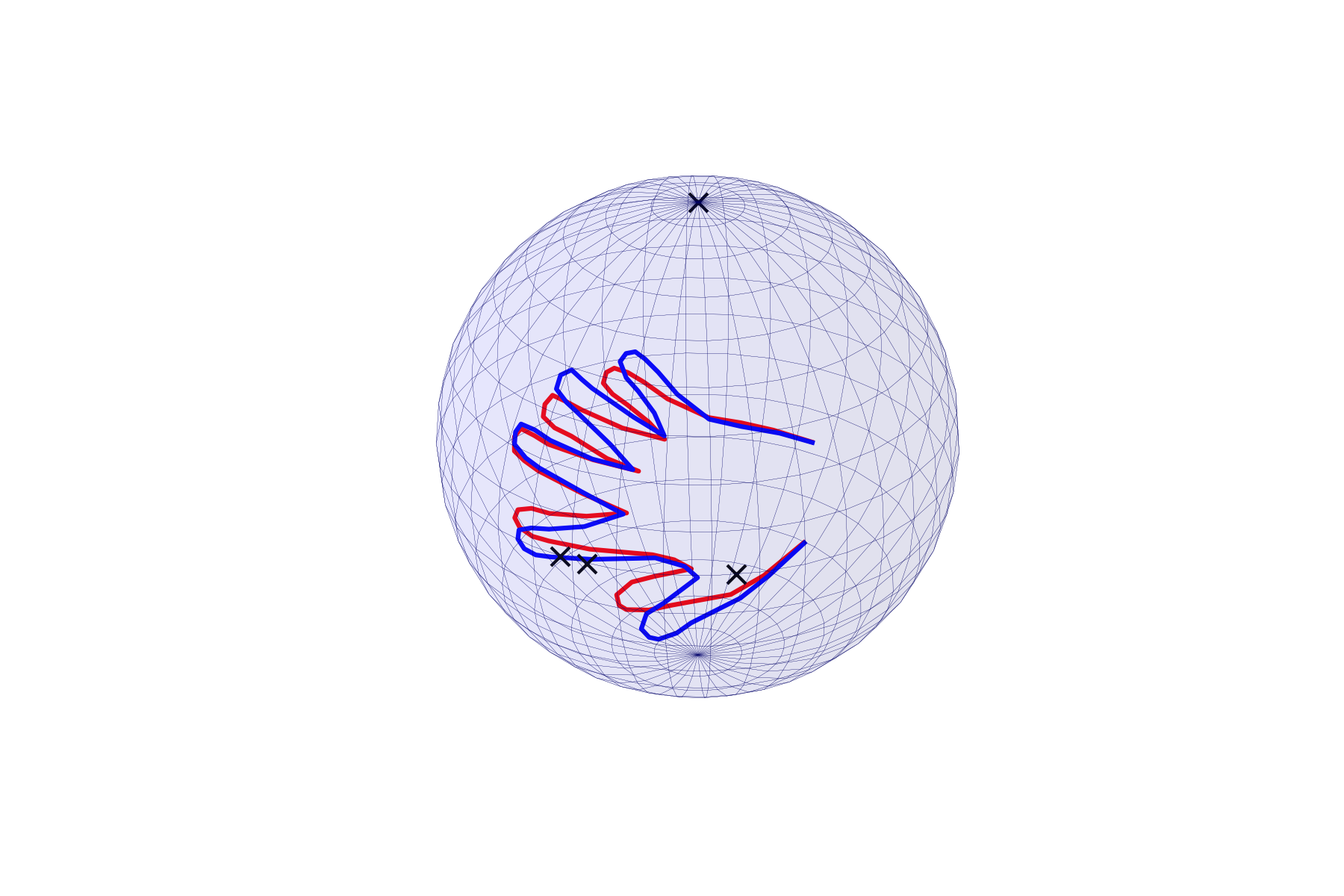
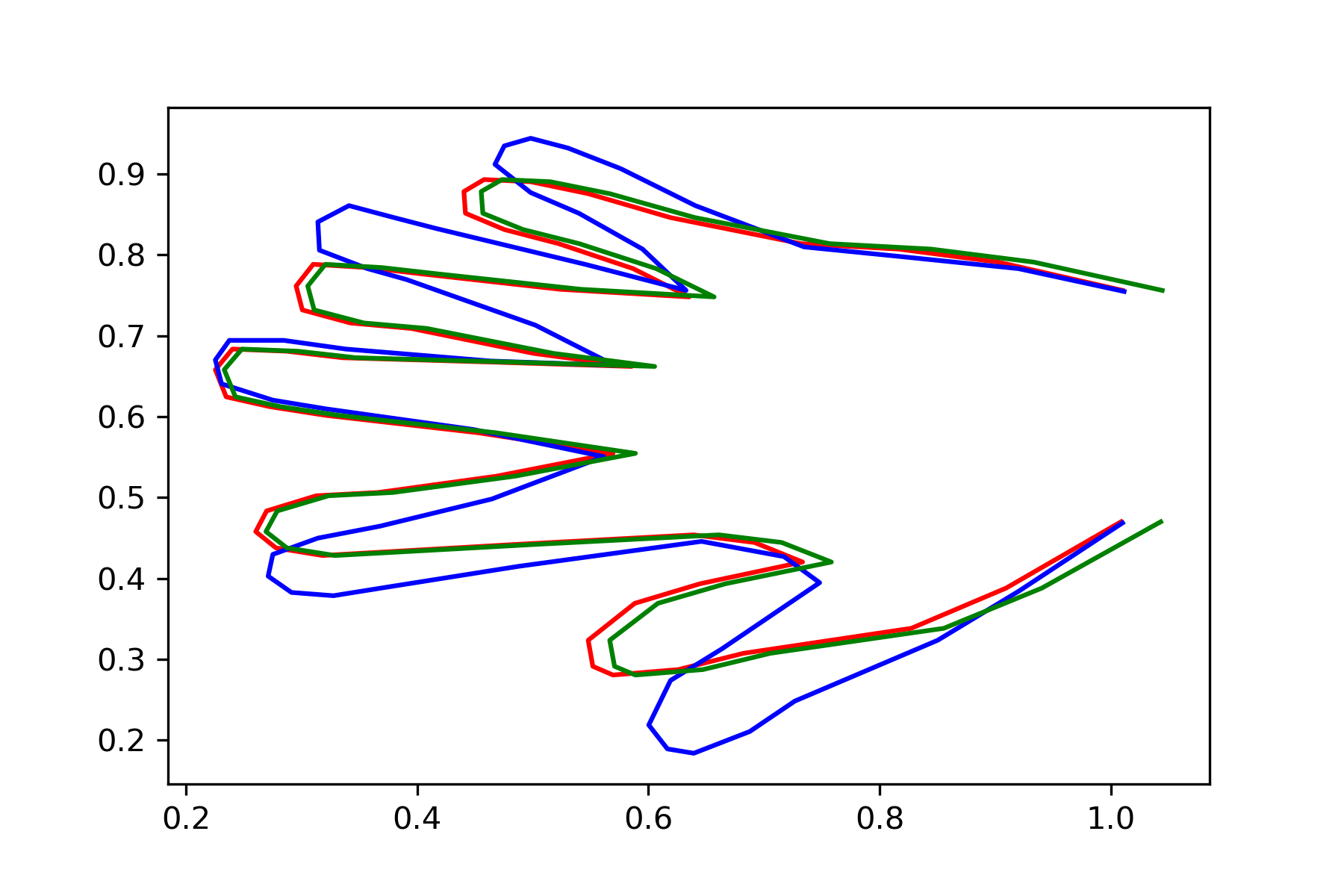
For \( i \in \{0,1,2,3\}\):
\(T_{x_i} S^2 \)
Compute \(A_{x_i} \)



\(d(A_{x_0}H_1,A_{x_1}H_1):\) 0.082
\(d(A_{x_0}H_1,A_{x_2}H_1):\) 0.367
\(d(A_{x_0}H_1,A_{x_3}H_1):\)0.350
\(d(H_2,A_{x_0}H_1):\) 0.473
\(d(H_2,A_{x_1}H_1):\) 0.5032
\(d(H_2,A_{x_2}H_1):\) 0.4702
\(d(H_2,A_{x_3}H_1):\)0.5506
\(log_{x_0}\)
\( exp_{x_0}\)
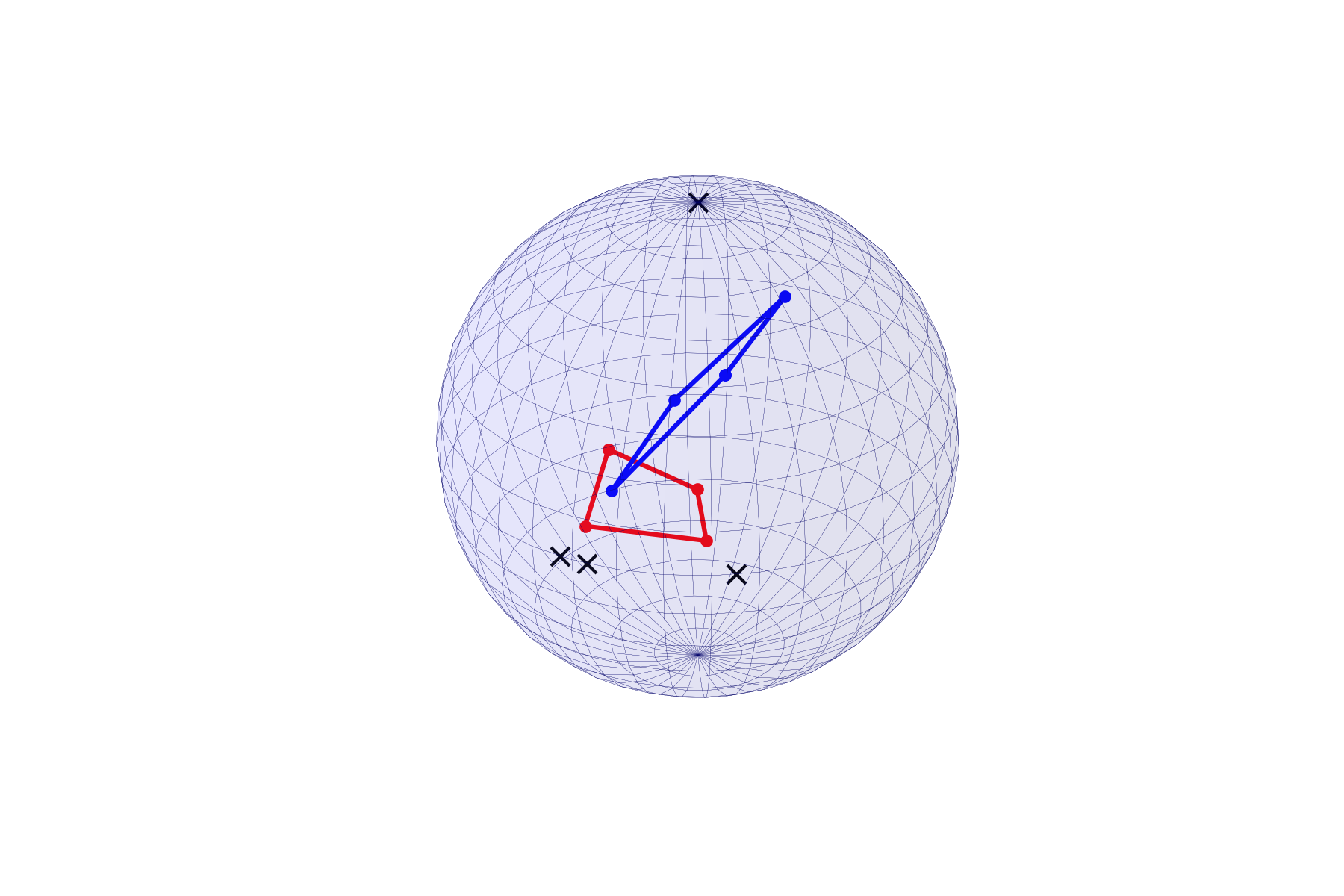
For \( i \in \{0,1,2,3\}\):
\(T_{x_i} S^2 \)
Compute \(A_{x_i} \)
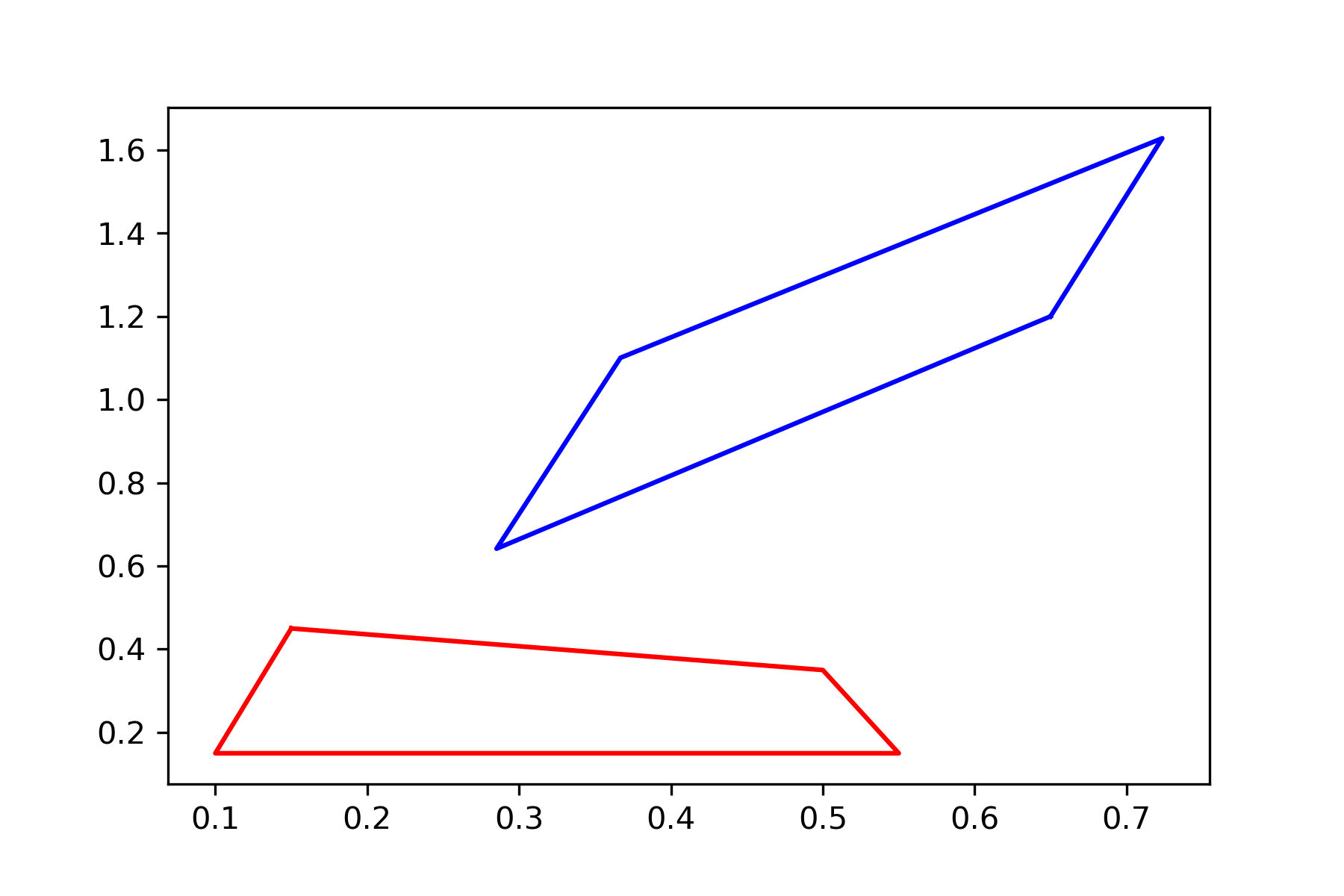
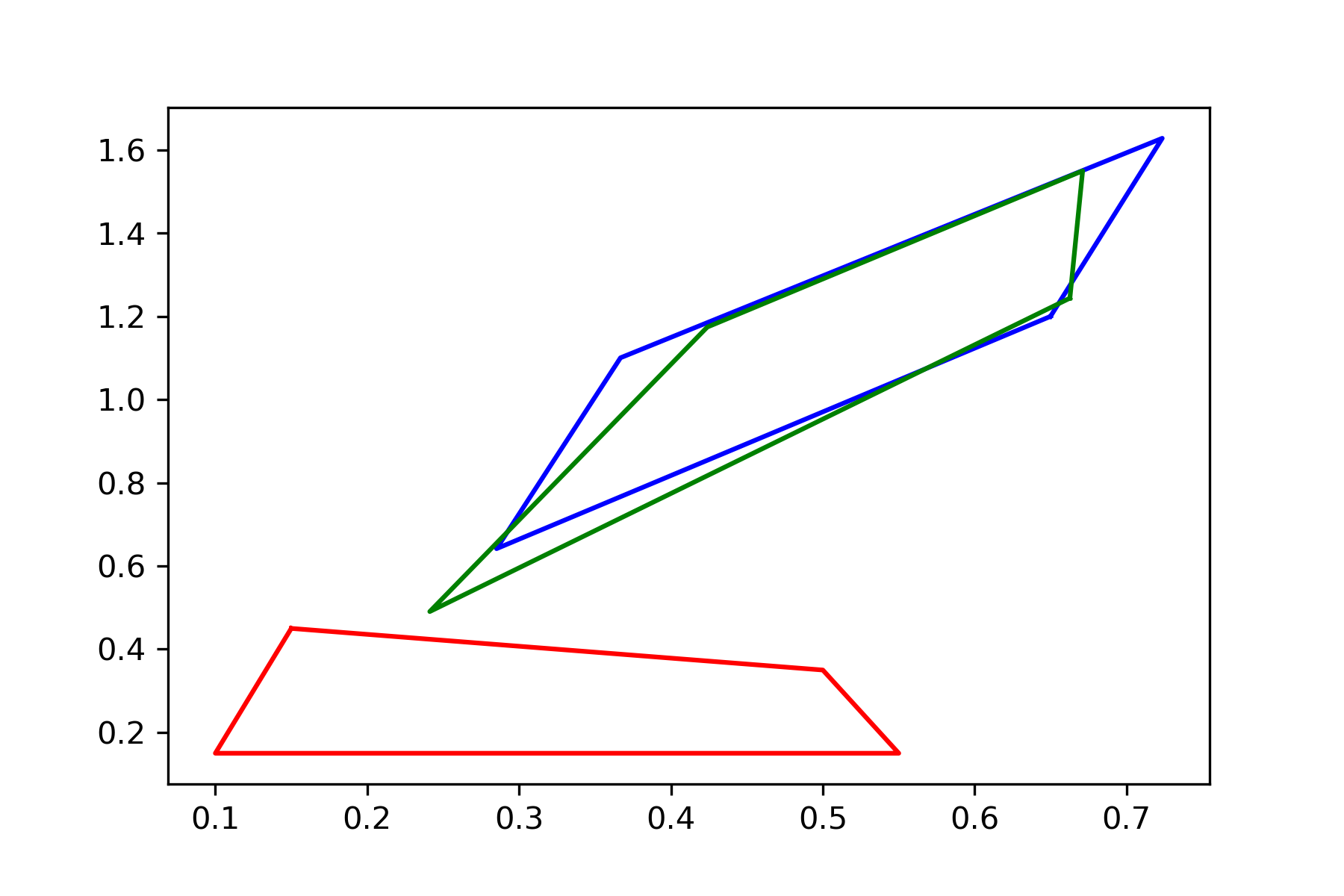
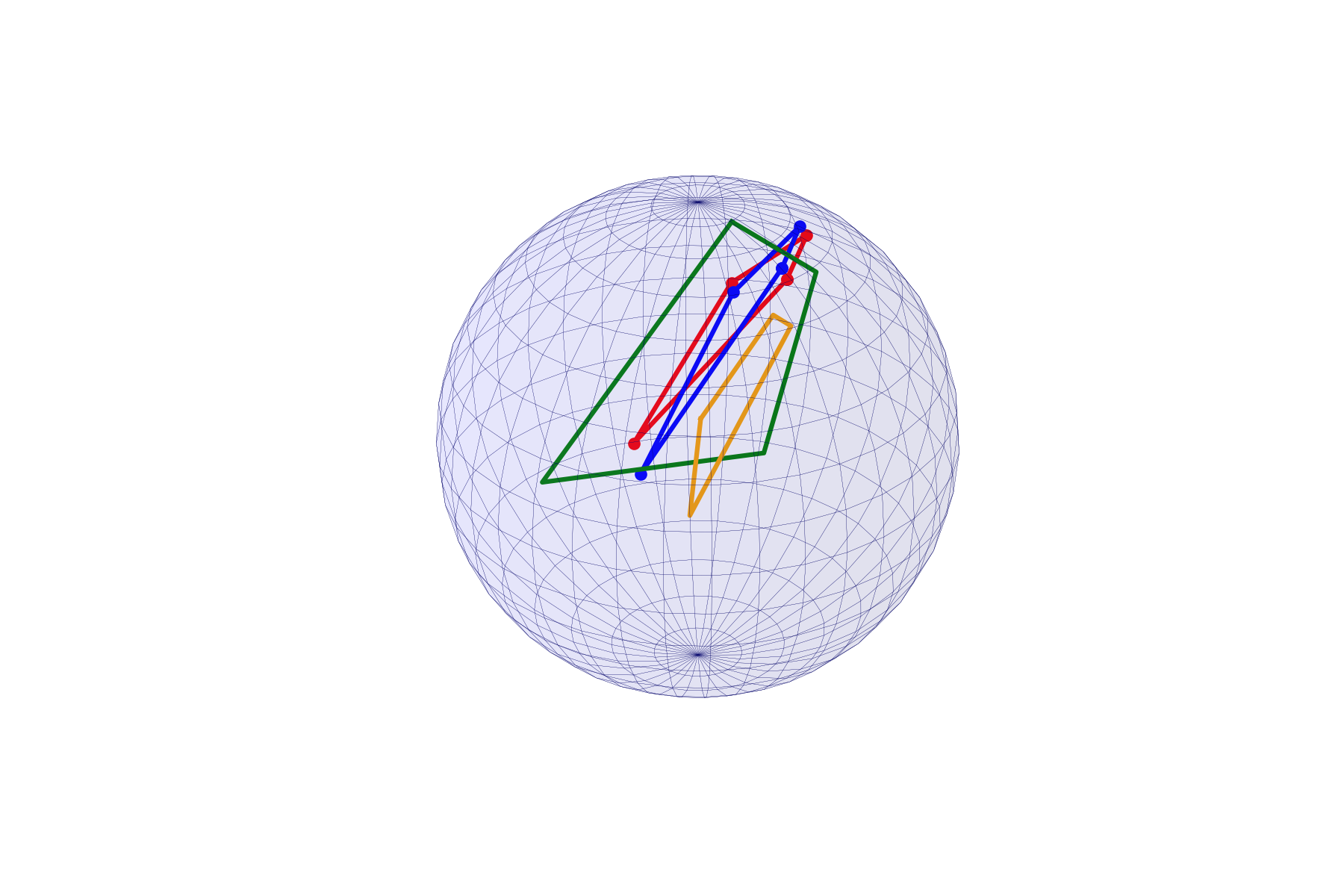
\(d(A_{x_0}H_1,A_{x_1}H_1):\) 0.1515
\(d(A_{x_0}H_1,A_{x_2}H_1):\) 0.909
\(d(A_{x_0}H_1,A_{x_3}H_1):\)1.1004
\(d(H_2,A_{x_0}H_1):\) 1.0193
\(d(H_2,A_{x_1}H_1):\) 1.0081
\(d(H_2,A_{x_2}H_1):\) 1.1205
\(d(H_2,A_{x_3}H_1):\)1.2281
Thank you for listening!