AutoGrad

Peter

Intro

Deep leaning

Gradient Based learning

How to Compute Gradient?

1. Symbolic Diff

Use Symbol

like what you do in Calculus class

Sympy

http://www.sympy.org/en/index.html

2.Numerical Diff

Approximate the derivative 

Simplest

3. Automatic Diff

Build Computational Graph

Computational Graph

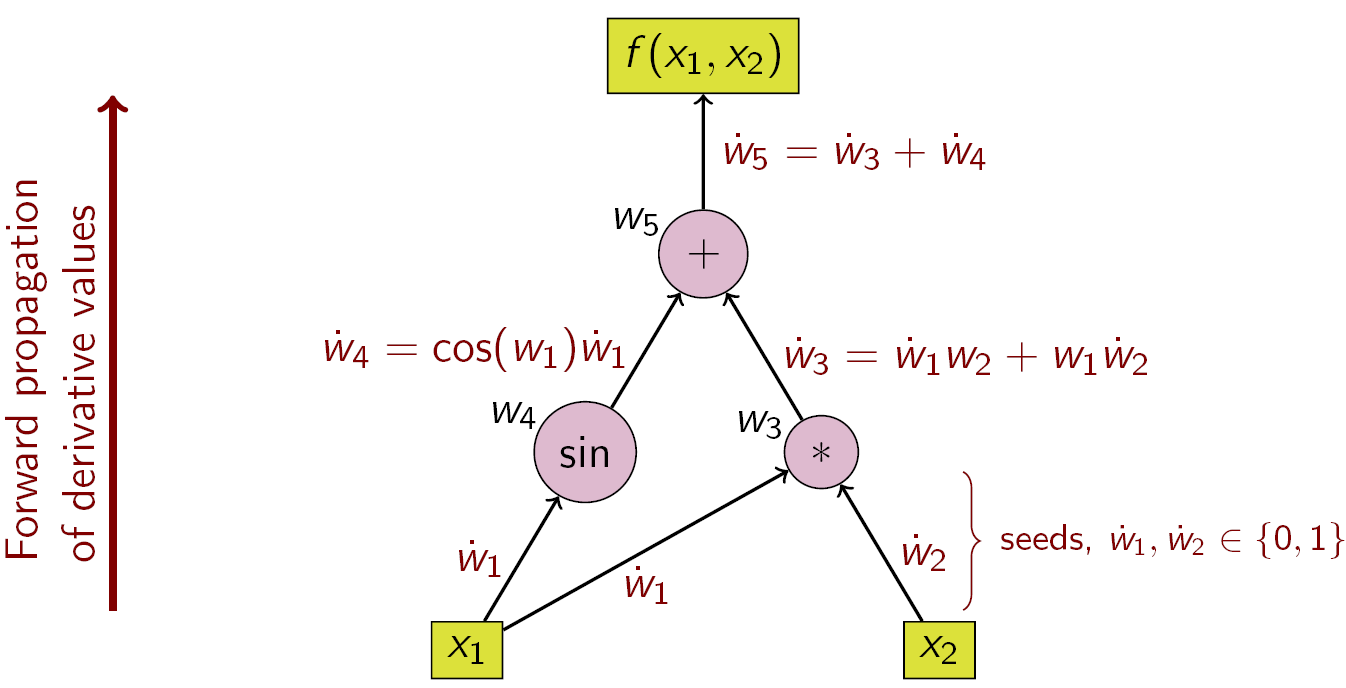
wiki

Two kinds of Computational Graph

Static v.s. Dynamic

Static

• Theano
• Tensorflow
• Caffe
• Mxnet

Dynamic

• PyTorch
• Mxnet
• Tensorflow Fold

Dynamic

Dynamic

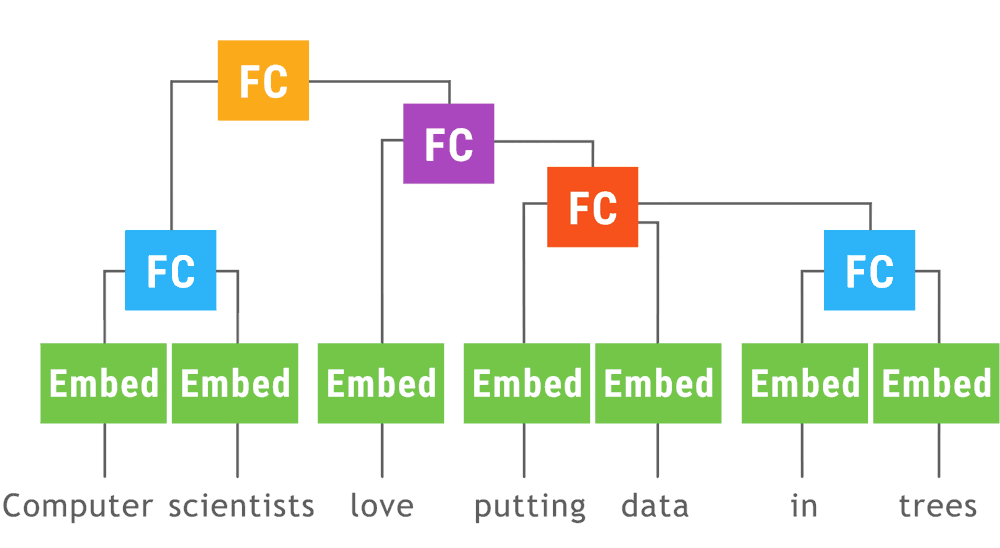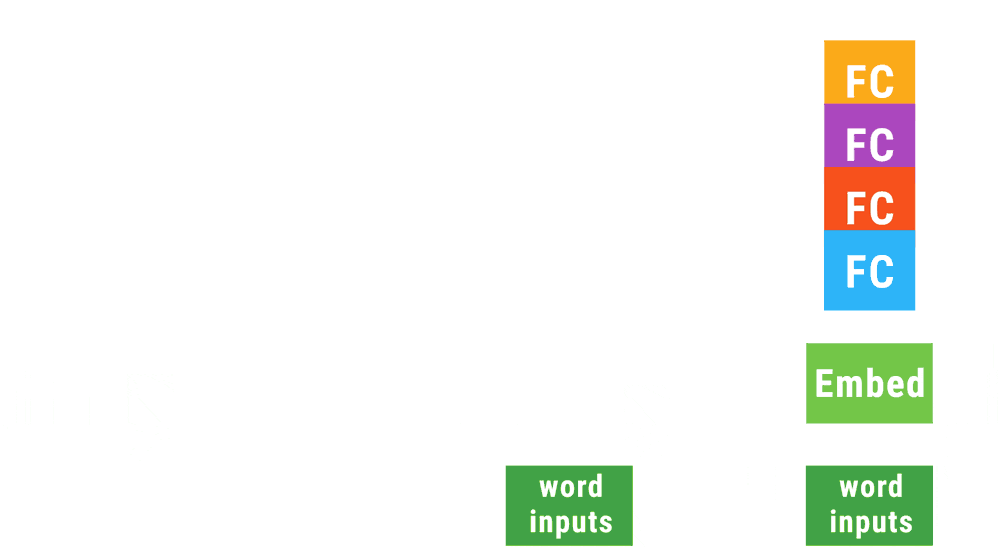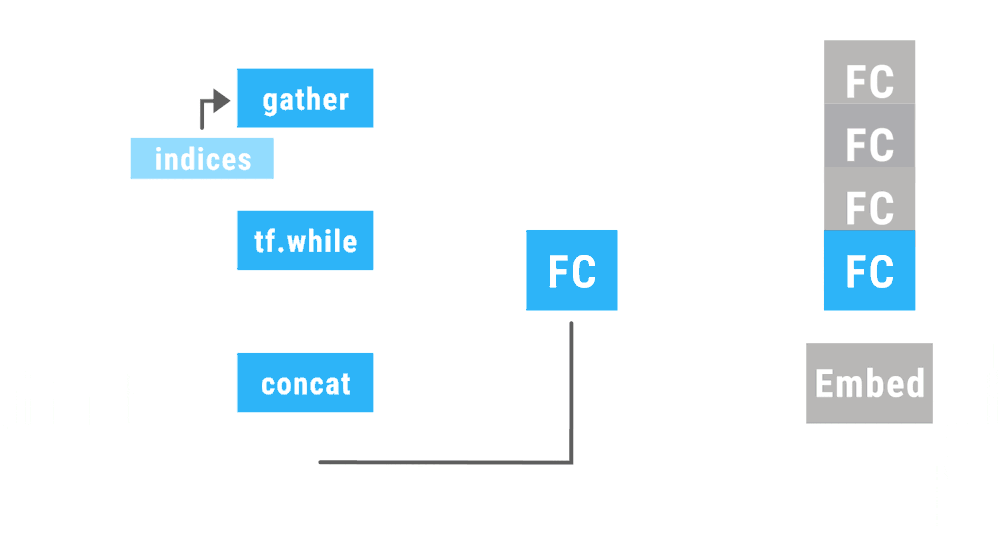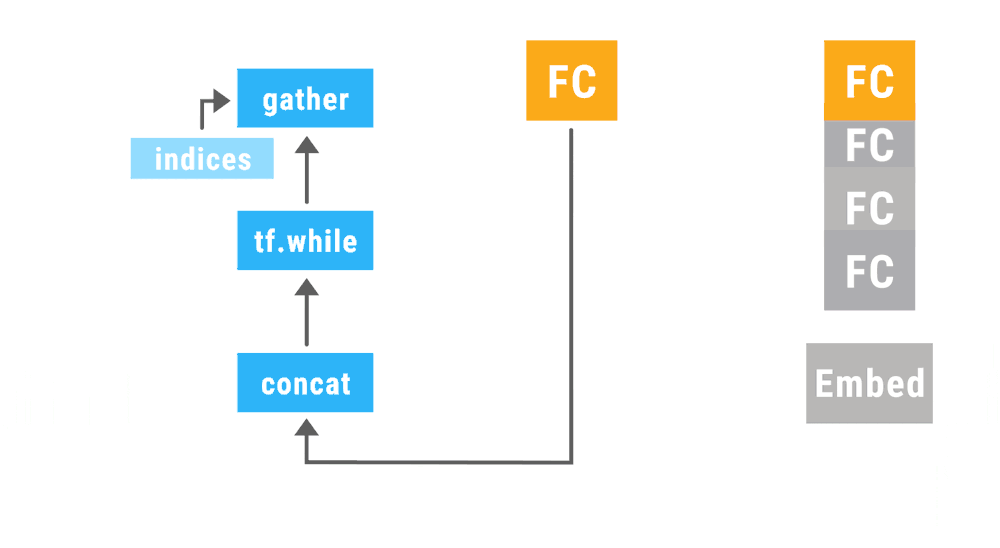
TensorFlow Fold

Pros & Cons

Static pros

• Optimization
• Portable

Static cons

• Hard to debug
• Controll flow 

Dynamic

• Easy to debug
• Control flow
• Dynamic structure

Autograd

HIPS/autograd

Compute Gradient in

Plain Python

>>> import autograd.numpy as np  # Thinly-wrapped numpy
>>> from autograd import grad    # The only autograd function you may ever need
>>>
>>> def tanh(x):                 # Define a function
...     y = np.exp(-x)
...     return (1.0 - y) / (1.0 + y)
...
>>> grad_tanh = grad(tanh)       # Obtain its gradient function
>>> grad_tanh(1.0)               # Evaluate the gradient at x = 1.0
0.39322386648296376
>>> (tanh(1.0001) - tanh(0.9999)) / 0.0002  # Compare to finite differences
0.39322386636453377

>>> import matplotlib.pyplot as plt
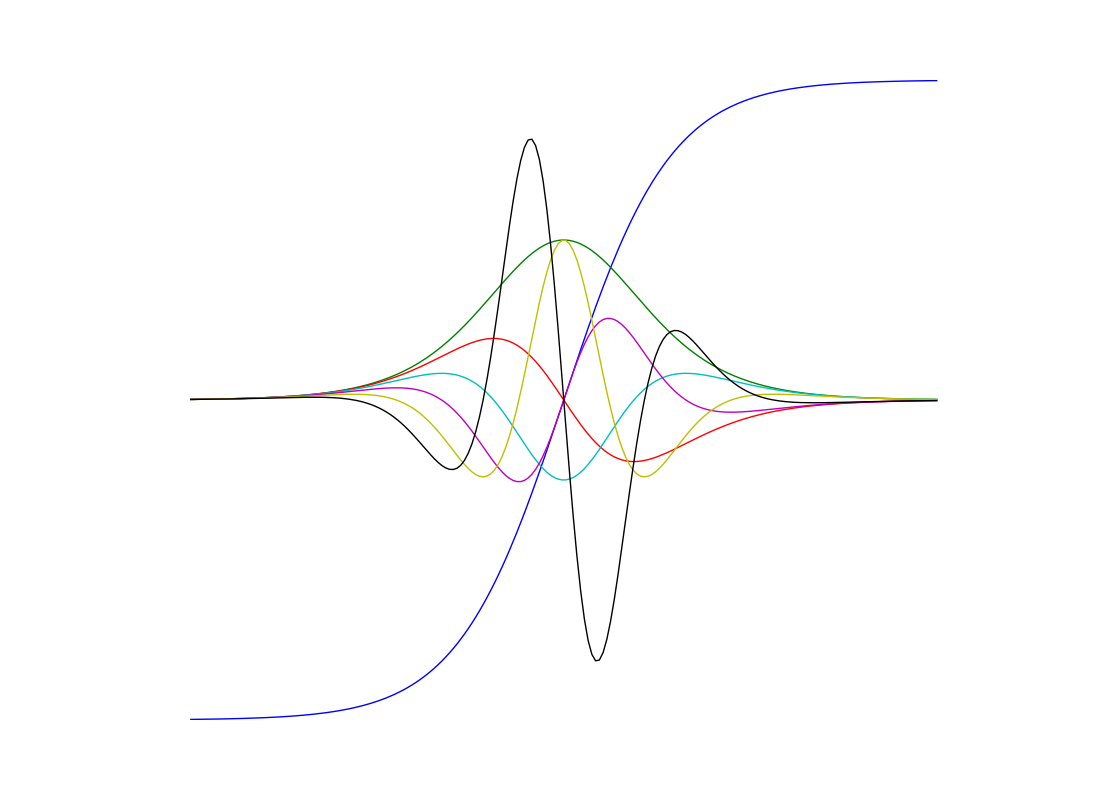
>>> x = np.linspace(-7, 7, 200)           # grad broadcasts across inputs
>>> plt.plot(x, tanh(x),
...          x, grad(tanh)(x),                                # first  derivative
...          x, grad(grad(tanh))(x),                          # second derivative
...          x, grad(grad(grad(tanh)))(x),                    # third  derivative
...          x, grad(grad(grad(grad(tanh))))(x),              # fourth derivative
...          x, grad(grad(grad(grad(grad(tanh)))))(x),        # fifth  derivative
...          x, grad(grad(grad(grad(grad(grad(tanh))))))(x))  # sixth  derivative
>>> plt.show()

Extendable

import autograd.numpy as np
from autograd.core import primitive

@primitive
def logsumexp(x):
    """Numerically stable log(sum(exp(x)))"""
    max_x = np.max(x)
    return max_x + np.log(np.sum(np.exp(x - max_x)))

def logsumexp_vjp(g, ans, vs, gvs, x):
    return np.full(x.shape, g) * np.exp(x - np.full(x.shape, ans))

logsumexp.defvjp(logsumexp_vjp)

from autograd import grad
def example_func(y):
	z = y**2
	lse = logsumexp(z)
	return np.sum(lse)

grad_of_example = grad(example_func)
print "Gradient: ", grad_of_example(np.array([1.5, 6.7, 1e-10])

Support Complex Number!

Multivariable function

import autograd.numpy as np
from autograd import grad

def sigmoid(x):
    return 0.5*(np.tanh(x) + 1)

def logistic_predictions(weights, inputs):
    # Outputs probability of a label being true according to logistic model.
    return sigmoid(np.dot(inputs, weights))

def training_loss(weights):
    # Training loss is the negative log-likelihood of the training labels.
    preds = logistic_predictions(weights, inputs)
    label_probabilities = preds * targets + (1 - preds) * (1 - targets)
    return -np.sum(np.log(label_probabilities))

# Build a toy dataset.
inputs = np.array([[0.52, 1.12,  0.77],
                   [0.88, -1.08, 0.15],
                   [0.52, 0.06, -1.30],
                   [0.74, -2.49, 1.39]])
targets = np.array([True, True, False, True])

# Define a function that returns gradients of training loss using autograd.
training_gradient_fun = grad(training_loss)

# Optimize weights using gradient descent.
weights = np.array([0.0, 0.0, 0.0])
print "Initial loss:", training_loss(weights)
for i in xrange(100):
    weights -= training_gradient_fun(weights) * 0.01

print  "Trained loss:", training_loss(weights)