
About Quantum Computing.
<它>是甚麼 ?
現代的生活中
我們時不時就可以聽到什麼
"量子電腦"、"量子運算"、"超級運算能力"
光在Google上就可以找到大約450多萬筆資料
聽起來好像又是跟AI同樣的異世界事物
但是它真的這麼難理解嗎?
它又會對未來生活造成什麼影響呢?
讓我們繼續看下去...
在進行解說之前...
先看超高品質影片啦><
(觀看數有1151萬呦 ! 排名第一 !
就如同大家所看到的,
量子計算將為我們各位人類帶來:
-
醫療進步
-
更好的加密方法
-
更快的資料庫搜尋
-
強人工智慧的實現
-
物化領域的模擬與深入
-
找到對結構更堅固、好用的材料
-簡而言之,就是方法會變得越來越好,越來越快。
但是......在量子計算之前,就要先有
量子電腦。
其實就是右邊這個東東 \(\rightarrow\)
\(\leftarrow\) 還有這個

在製作量子電腦之前...
我們就必需要知道如何在現實中
做出量子位元。
因此,接下來將介紹目前製作量子位元的方法。
(不過詳細製作方法請自行查詢)
1. 超導迴路
原理是以水銀在 \(4.2 K(-268.95^{\circ}C)\) 溫度下時電阻為 \(0\) 的方法,
讓電流可以在其中無消耗地持續流動。
優點:
錯誤率低 (邏輯上約為 99.4%)
快速 (可利用現有材料製作)
缺點:
壽命短 (只有 0.00005秒),這也是疊加態能夠維持的最小時間。
保存溫度須很低
2. 離子阱
原理是使用電場以及磁場的組合,
來捕捉與外界系統隔離之帶電質點 (離子),
再使用雷射操控。
優點:
壽命長
成功率比超導迴路還要高 (99.9%)
缺點:
操作速度較慢 (需要許多雷射)
3. 拓撲量子位元
優點:
穩定,沒有誤差
缺點:
目前仍只是純理論
此方法目前為純理論 (代研究中)
4. 鑽石空缺
原理是利用鑽石本身的表面原子尺度空缺、
或是利用電子束衝撞而產生的空缺,
讓鑽石晶格多了電子,並運用雷射進行操作。
優點:
高壽命 (10秒)
高成功率 (99.2%)
>>於室溫下可運作!
缺點:
表面只有大約 2% 的空缺
糾纏態不易製備
製作好了量子位元之後,還要符合
迪文森佐準則 (DiVincenzo criteria)
1. 具有可掌控的量子位元,並具有可擴展性。
2. 能夠將量子位元初始化到一個簡單的量子態。
3. 能在較長時間內保持量子相干性,或者說退相千時間要遠大於量子邏輯門操作時間。
4. 能夠進行普適量子邏輯門操作。
5. 能夠進行單量子位元的測量。
為什麼呀(?~?)
因為這樣,
才可以滿足要在真實物理系統裡做量子計算所需要的
最基本運作狀態。
(其實後來還有加入下列兩條,是有關實現量子計算機網路的基本需求。)
6. 本地量子位元和飛行量子位元能夠互相轉化。
7. 能夠在兩地間傳播飛行量子位元。
Linear Algebra
Q: 為什麼要先學基本的線性代數 ?
A: 所有需要計算量子態的地方都會用到!
\(\langle\)向量\(\rangle\)
-
具有大小、方向的一個物件
-
有自己的運算法則
ex: \(\vec{a},\ \bold{a}\)
-
普通都是 2、3 維
-
量子運算需要的是高維複數空間 (希爾伯特空間)
(Vector)
普通的向量:
量子運算中的向量:

\(\vec{a}=(0,1)\)
\(\bold{a}=(1+2i,\ 5-3i)\)
-
向量內積 (Dot product)
\(\vec{a} \cdot \vec{b}=\sum_{i=1}^{n} a_{i}b_{i}\)
\(\vec{a},\vec{b}\in\mathbb{R}^{n}\)
- 兩正交向量之間內積為0
- 結果為一純量
-
向量外積 (Cross product)
\(\vec{a} \times \vec{b}=||\vec{a}||\,||\vec{b}||\,sin(\theta)\bold{n}\)
"范數"、"模長"
\(\bold{n}\cdot\vec{a}=\bold{n}\cdot\vec{b}=0\)
- 其結果為一向量 (除了\(sin(\theta)=0\))
- \(\rightarrow\)兩平行向量外積為0
- 僅限三維
正交性 (Orthogonality)
\(\langle\)複數\(\rangle\)
-
可表達在二維平面上的一點
-
有旋轉等作用時方便操作
\(z=1+i\)
\(\Re\)
\(\Im\)
(Complex Number)

一些性質
-
輻角 (Argument)
\(z=1+i\)
\(\Re\)
\(\Im\)
\(\varphi\)
\(\rightarrow arg(z)=\frac{\pi}{4}\)
取絕對值的意義 \(\rightarrow\) 長度
(模 (Modulus)、輻值)
\(z=1+i\)
\(\Re\)
\(\Im\)
\(|z|\)
\(\rightarrow|z|=\sqrt{2}\)
稍微提一下:
\(e^{i\theta}=cos(\theta)+isin(\theta)\)
因此,一複數可表達為:
\(z=|z|cos(arg(z)) + i|z|sin(arg(z))\)
\(\rightarrow |z|e^{iarg(z)}\)
\(\rightarrow re^{i\varphi}\)
複數相乘
\(r_{1}e^{i\varphi}\cdot r_{2}e^{i\phi}\)
\(=r_{1}r_{2}\cdot e^{i(\varphi + \phi)}\)
\(=r'e^{i\psi}\)
-
長度相乘
-
輻角相加
-
結果為複數
共軛 (Conjugate)
\(z=1+3i\)
\(\rightarrow \bar{z}=z^*=1-3i\)
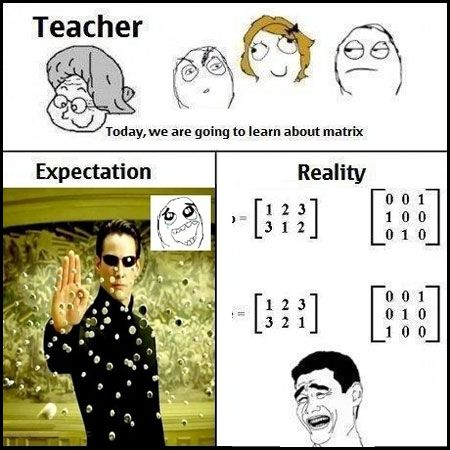
\(\langle\)矩陣\(\rangle\)
-
用於描述線性變換等作用
(Matrix)
\(A_{3\times 4}=\begin{bmatrix}1 & 1 & 1 & 1\\ 1 & 2 & 3 & 4\\ 1 & 3 & 6 & 10\end{bmatrix}\)
\(row\)
\(column\)
\(\begin{bmatrix}a & b\\c & d\end{bmatrix}\begin{bmatrix}n_{1} & n_{2} & n_{3}\\ n_{4} & n_{5} & n_{6}\end{bmatrix}=\)
\(\begin{bmatrix}a[n_{1}\quad n_{2}\quad n_{3}] + b[n_{4}\quad n_{5}\quad n_{6}]\\c[n_{1}\quad n_{2}\quad n_{3}] + d[n_{4}\quad n_{5}\quad n_{6}]\end{bmatrix}\)
加法
乘法
\(\begin{bmatrix}a & b\\ c & d\end{bmatrix}+\begin{bmatrix}e & f\\ g & h\end{bmatrix}=\begin{bmatrix}a+e & b+f\\ c+g & d+h\end{bmatrix}\)
\((\)
\((\)
\((\)
\((\)
Step 2
Step 1
Step 3
Step 4
看乘法詳細步驟 \(\downarrow\)
轉置 (Transpose)
\(A=\begin{bmatrix}1 & 2\\ 3 & 4\\ 5 & 6\end{bmatrix}\)
\(A^T=\begin{bmatrix}1 & 3 & 5\\ 2 & 4 & 6\end{bmatrix}\)
\(|\varphi\rangle = cos(\frac{\theta}{2})|0\rangle + e^{i\phi}sin(\frac{\theta}{2})|1\rangle\)
但這個是什麼?~?
Linear Algebra
Dirac Notation Part
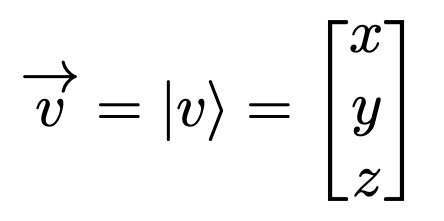
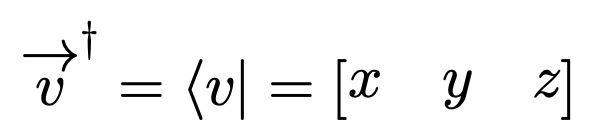
Bra - Ket Notation
Ket
Bra
內積表示法
\(\langle \phi | \varphi\rangle\)
-
Dot product between \(|\phi\rangle\) and \(|\varphi\rangle\)
(共軛轉置矩陣)
\(A=\begin{bmatrix}1 & 1-2i\\ 1+i & 1\end{bmatrix}\)
\(A^\dagger =\begin{bmatrix}1 & 1-i\\ 1+2i & 1\end{bmatrix}\)
矩陣的埃爾米特伴隨 (Hermitian adjoint)
Text
Basic concepts part.1
首先......<Qubit(量子位元)>
同時是1,同時是0 ??
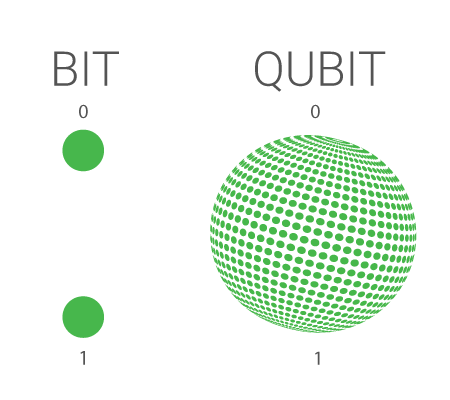
傳統的經典位元
只可以是 0 或 1 其中一個狀態
但是量子位元在疊加態時
卻可以同時是這兩種狀態
( 姆,什麼是疊加態 ? >~<
(等等介紹~
<小小的觀念說明>
\(Bit\) (經典位元) 指的是在典型電腦中所使用的位元,
而 \(Qubit\) (量子位元) 指的是在量子電腦中所使用的位元。
經典位元有 0 或 1 兩種狀態,
而在同一時間只會是其中一種狀態。
0 是經典位元的基本態。
量子位元也可以是 0 或 1 的狀態,
我們以 \(|0\rangle\) 和 \(|1\rangle\) 來個別表示,
\(|0\rangle\) 也是一個量子位元的基本態。
<小小的觀念說明>
<小小的觀念說明>
但是與 \(Bit\) 不同的是,
\(Qubit\) 在同一時間內且未被觀察前,
同時可以是 \(|0\rangle\) 與 \(|1\rangle\)。
觀察後究竟會是哪一個,就要取決於在疊加
態時有多少的機率是 \(|0\rangle\),
多少的機率會是 \(|1\rangle\)。
\( |\psi\rangle = \alpha |0\rangle + \beta |1\rangle , \alpha ,\beta \in \mathbb{C}, \left | \alpha \right |^{2} + \left | \beta \right |^{2} = 1 \)
The state of a qubit.
在此定義中,\( \left | \alpha \right |^{2} \)
代表著此\(Qubit\)被觀察到後,為0的機率
相對的,\( \left | \beta \right |^{2} \)
就是代表著此\(Qubit\)被觀察到後,為1的機率
一個量子的狀態,可以被描繪在布洛赫球面(Bloch Sphere)上
球頂,就表示狀態為 \( |0 \rangle \) 的 \(Qubit\)
球底,就表示狀態為 \( |1 \rangle \) 的 \(Qubit\)
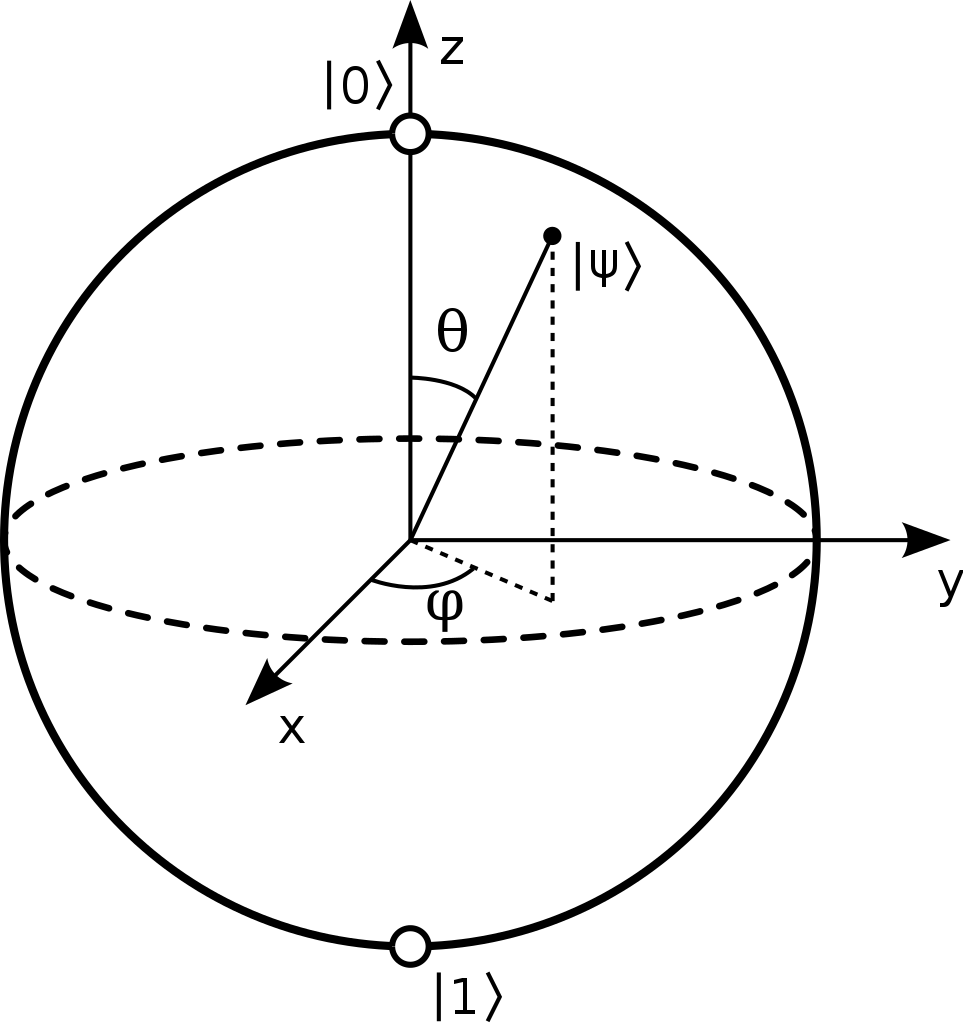
(接下將把"量子態"簡寫為 "QS" (Qubit State))
(這個其實是一種叫做
"球座標"的表示方法
單個 \(Qubit\) 的狀態 :
\( |\psi\rangle = \alpha |0\rangle + \beta |1\rangle\)
也可以被寫成一個向量\~\
\( \begin{bmatrix} \alpha \\\beta \end{bmatrix} \)
\( \alpha |0\rangle + \beta |1\rangle \rightarrow\)
\(|0\rangle = \begin{bmatrix} 1\\0 \end{bmatrix}\)
\(|1\rangle = \begin{bmatrix} 0\\1 \end{bmatrix}\)
小小的由來解釋
為什麼會將 QS
表示在單位圓上呢?
原因是來自於定義的 \(\left | \alpha \right |^{2} + \left | \beta \right |^{2} = 1\)
對於這個的第一印象,
就是與\(cos(\theta)^{2}+sin(\theta)^{2}=1\) 相似,
所以就引進了
\(\left | \alpha \right |=cos(\theta),\ \left | \beta \right |=sin(\theta)\)
的表示法。
此部分為大電神林尚廷學長做出的完備解釋\^~^\
此處可懸(?)\(\rightarrow\)
但是那是絕對值,
而在事實上還有另外一種叫做
"相位" 的東西,
所以還要再加上相位的部分。
\(\alpha = cos(\theta)e^{i\delta},\ \beta=sin(\theta)e^{i\psi}\)
(小小補充 :
對複數取絕對值是代表這個複數
與原點的距離,
而 \(\left |e^{i\theta} \right |,\ \theta \in \mathbb{N},\ \) 恆等於 1)
在這其中,
其實有一個名叫為 "共同相位 \((\delta)\)" 的東西。
物理學家發現這個共同相位在量子閘操作下,
不會影響到測量機率。
(也就是說共同相位對 \(|0\rangle\) 和 \(|1\rangle\)
造成的機率影響都一樣)
\(\alpha = cos(\theta),\ \beta=sin(\theta)e^{i\varphi},\ \varphi=\psi-\delta\)
(就是把兩個相位同時減去共同相位~)
所以可以把 \(\alpha\) 和 \(\beta\) 再簡化,
變成下列的定義。
但是 \(|0\rangle\) 和 \(|1\rangle\) 的機率都是 0 ~ 1,
所以 \(\theta\) 的範圍應該要為 \(0\degree\leq \theta\leq 90\degree\)
想要將 QS 依照下列的方式放到球上時,
我們卻發現 \(\theta\) 的範圍為 \(0\degree\leq \theta\leq 180\degree\)
所以我們必須要把 QS 定義中的 \(\theta\) 改為 \(\frac{\theta}{2}\)。

\(\frown\)
\(\pi(rad)\)
因此, QS 可以使用下列的式子表達~
\(|\varphi\rangle=e^{i\delta}(cos(\frac{\theta}{2})|0\rangle+sin(\frac{\theta}{2})e^{i\varphi}|1\rangle)\)
傳說中的共同相位
叫做 "相對相位"
的東東
而在計算上,
我們會選擇使用簡化過後的式子
(省去沒有物理意義的共同相位)
\(\rightarrow |\varphi\rangle=cos(\frac{\theta}{2})|0\rangle+sin(\frac{\theta}{2})e^{i\varphi}|1\rangle\)
相對&共同相位的介紹
-
為什麼相對相位會被稱作為
相對相位呢?
這是因為在物理學上,
有意義的只有兩個相位之間的差值
所以會被稱作為 "相對的相位"。
我們不可能觀測到共同相位的度數,
所以其實共同相位是多少都沒關係。#^#
還有其實......
(存在又不存在的共同相位(@^@??)
不然其實原本包括共同相位的定義
是要使用到四維空間才能表示的
(因為有兩個不同的複數(&^&))
(所以猜測可能是故意讓其中一個複數變不見當作定義會比較好算且可用三維空間座標表示(?)
所以剛剛的定義......
\(\alpha = cos(\theta),\ \beta=sin(\theta)e^{i\varphi},\ \varphi=\psi-\delta\)
如果當初是以下列為定義
也沒問題呦$^$~
\(\alpha = cos(\theta)e^{i\phi},\ \beta=sin(\theta),\ \phi=\delta-\psi\)
~座標介紹篇~
<這裡的是座標的部分,
所以角度會是 \(\theta\) >
我們剛剛已經知道了 QS 的定義,
接下來要使用這個定義把 QS 表示在球面上
\\~^~^\\
\(|\varphi\rangle=cos(\theta)|0\rangle+sin(\theta)e^{i\varphi}|1\rangle\)
\(0\degree \leq \theta \leq 180\degree,\ 0\degree \leq \varphi \leq 360\degree\)
解剖時間 !
\(|\varphi\rangle=cos(\theta)|0\rangle+sin(\theta)e^{i\varphi}|1\rangle\)

紅色的部分為 \(|\psi\rangle\) 的 \(z\) 座標值
但是橘色部分同時
代表了 \(x\) 和 \(y\) 座標
為什麼呢 \(?~?)
(數學解釋請看下一張
~(=^・ω・^=)
(補充 : 這裡的 \(xy\) 是複數平面)
\(\theta\)
\(r\)
如圖是一個複數平面
上面有一個複數 \(z_{1}\)。
當我們知道 \(|z_{1}|\)(模長)(圖中的\(r\))
與 \(arg(z_{1})\)(輻角)(圖中的\(\theta\)),...
\(z_{1}\)
\(x^{+}(Re)\)
\(y^{+}(Im)\)
我們就可以使用下列的公式
表示出這個複數 \^~^\
\(z=|z|cos(arg(z))+i|z|sin(arg(z))\)
\(\rightarrow z=|z|(cos(arg(z))+isin(arg(z)))\)
\(\rightarrow z=|z|e^{i\cdot arg(z)}\)
歐拉公式
橘色 = 紅色呦 > < !
附上漂亮的歐拉公式定義~^~^~
\(e^{i\theta}=cos(\theta)+isin(\theta),\ \theta (rad)\in\mathbb{R}\)
如果想要了解這個公式的由來的話,
可以去名叫做 "3Blue1Brown"
的 Youtube 頻道看看解釋呦 (^~^)
現在重新回來看這張圖......

\(|\varphi\rangle=cos(\theta)|0\rangle+sin(\theta)e^{i\varphi}|1\rangle\)
就是剛剛的模長
所以 \(|\psi\rangle\)
在三維空間中的座標,
就可以寫成下列這樣~^~^
\(\left\{\begin{matrix}x=sin(\theta)cos(\phi)\\ y=sin(\theta)sin(\phi)\\ z=cos(\theta)\end{matrix}\right.\)
超硬核的部分終於結束了...
回歸到 \(Gate\) 介紹篇囉 ! ~
再來介紹一個Gate
-
泡利-X閘(Pauli-X gate)
\( X = \begin{bmatrix}0 & 1\\1 & 0\end{bmatrix} \)
(這是它的旋轉矩陣形式
這個量子閘操作一個\(Qubit\)
作用是 "反轉量子態"
\( (|0\rangle\rightarrow |1\rangle, |1\rangle\rightarrow |0\rangle) \)
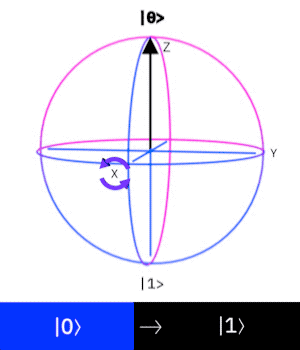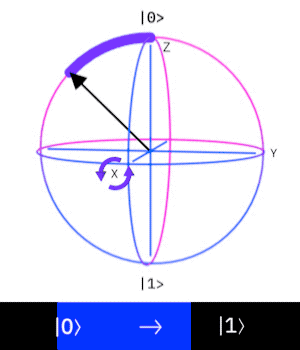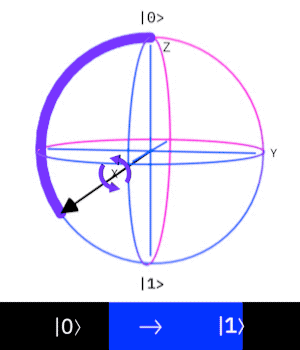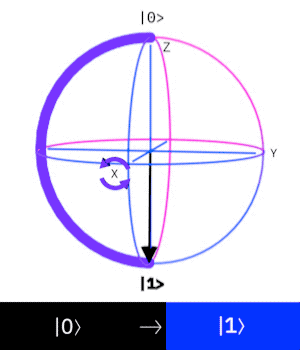
Quiz time!
-
請使用兩個量子閘,將 \(|0\rangle\) 變成 \(|0\rangle\)
Ans : \(X(X|0\rangle)\)
注意到了嗎 ?
對一個 \(Qubit\) 重複操作兩次這個量子閘,
等同於沒操作一樣。
(這是廢話嗎www(不一定喔(?
點它看答案 \(\rightarrow\)
所謂<疊加態\((Superposition)\)>
疊加態是指,
如果一個 \(Qubit\) 被觀察時
同時具有 \(|0\rangle\) 和 \(|1\rangle\)的可能性
那就代表這個 \(Qubit\) 處於疊加態。
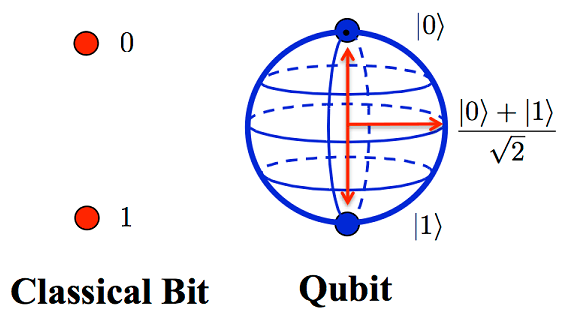
如圖,一個同時擁有
50% 機率為 \(|0\rangle\),50% 機率為 \(|1\rangle\)的\(Qubit\)
通常會被表示為 :
\(\frac{|0\rangle + |1\rangle}{\sqrt{2}}\) or \(\frac{|0\rangle - |1\rangle}{\sqrt{2}}\)
也可以被寫為 :
\(|+\rangle\) 或 \(|-\rangle\)
兩者雖然只差了一個負號,機率也相同,
但是實質上不一樣。
(姆,那要怎麼把\(Qubit\) 變成疊加態呢?~?
另一個Gate
-
阿達馬閘(Hadamard gate)
\(H = \frac{1}{\sqrt{2}}\begin{bmatrix}1 & 1\\ 1 & -1\end{bmatrix}\)
(這是它的旋轉矩陣型態
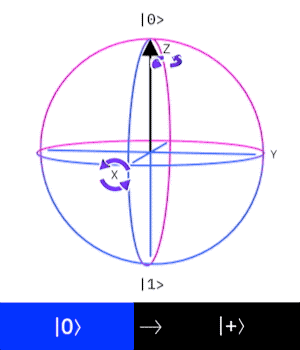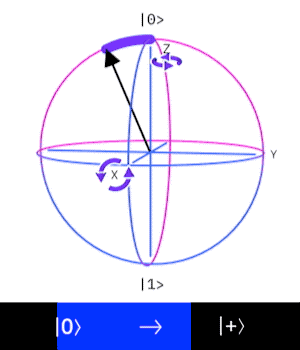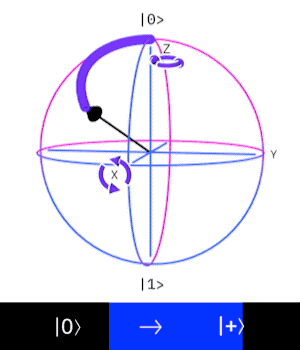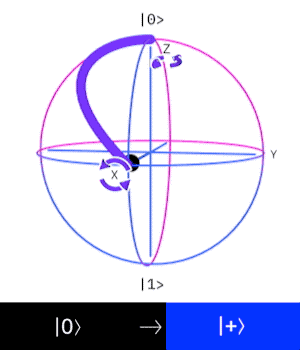
這個量子閘操作一個 \(Qubit\),
作用是讓這個 \(Qubit\) 進入疊加態。
\((|0\rangle \rightarrow |+\rangle, |1\rangle \rightarrow |-\rangle)\)
更準確地說,是 50% 為 \(|0\rangle\), 50% 為 \(|1\rangle\) 的疊加態。
Quiz time again!
第一題點它 \(\rightarrow\)
第二題點它 \(\rightarrow\)
1. 請使用量子閘將\(|0\rangle\) 變成 \(\frac{|1\rangle - |0\rangle}{\sqrt{2}}\)
2. 請使用\(Hadamard\ Gate\)將 \(|0\rangle\) 變成 \(|0\rangle\)
Ans : \(X(H(X|0\rangle))\)
Ans : \(H(H|0\rangle)\)
發現了嗎 ?
剛剛對於 \(X Gate\) 的重複操作效果
在 \(H Gate\) 上也會發生。^~^
又來Gate介紹
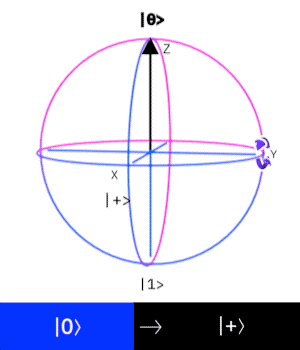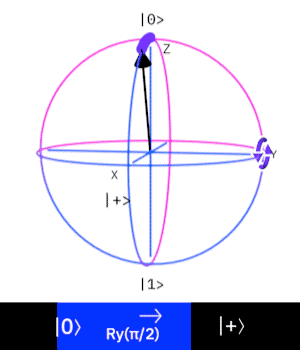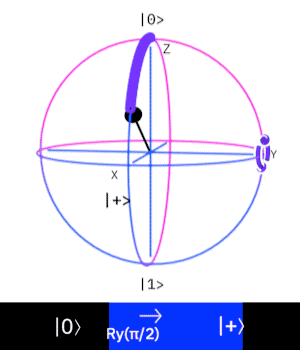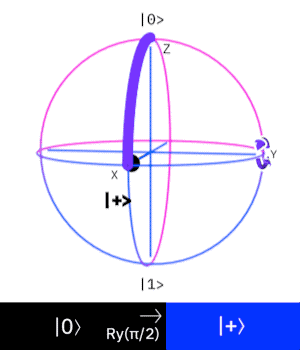
Ry Gate (Rotation Y Gate)
這個量子閘操作一個 \(Qubit\),
作用是在 \(Bloch Sphere\) 上旋轉 \(Y\)軸 \(\psi\) 度來改變量子態。
\(\begin{bmatrix}cos(\frac{\psi}{2}) & -sin(\frac{\psi}{2})\\ sin(\frac{\psi}{2}) & cos(\frac{\psi}{2})\end{bmatrix}\)
(這是它的旋轉矩陣形態)
注意注意注意注意注意注意
!~!
\(H \neq Ry(\frac{\pi}{2})\)
\(Ry(\frac{\pi}{2})\) 就只是讓 \(y\) 軸旋轉 \(\frac{\pi}{2}\) 度而已,
但是 \(H\ Gate\) 的行動模式較難描述...
<小小單元>
求出 \(H|\varphi\rangle\) 的通式
(非正式)
至目前為止的觀察,
\(H\ Gate\) 在三維空間中對 QS
造成的選轉可使用下列矩陣表達
\(H=\begin{bmatrix}0 & 0 & 1\\ 0 & -1 & 0\\ 1 & 0 & 0\end{bmatrix}\)
\(=\begin{bmatrix}x\\ y\\ z\end{bmatrix}\)
因此,
一個經過 \(H\ Gate\) 的量子態可以被寫成
\(H(|\varphi\rangle)=\begin{bmatrix}0 & 0 & 1\\ 0 & -1 & 0\\ 1 & 0 & 0\end{bmatrix}\begin{bmatrix}sin(\theta)cos(\phi)\\ sin(\theta)sin(\phi)\\ cos(\theta)\end{bmatrix}\)
\(=\begin{bmatrix}cos(\theta)\\ -sin(\theta)sin(\phi)\\ sin(\theta)cos(\phi)\end{bmatrix}\)
\(=\begin{bmatrix}z\\ -y\\ x\end{bmatrix}\)
其中新的位置的 \(\theta '\) 角
可以利用比對下列矩陣求出
\(\begin{bmatrix}cos(\theta)\\ -sin(\theta)sin(\phi)\\ sin(\theta)cos(\phi)\end{bmatrix}=\begin{bmatrix}sin(\theta ')cos(\phi ')\\ sin(\theta)sin(\phi ')\\ cos(\theta ')\end{bmatrix}\)
\(\rightarrow cos(\theta ')=sin(\theta)cos(\phi)\)
\(\theta '=cos^{-1}(sin(\theta)cos(\phi))\)
至於求出 \(\phi\) ...
目前使用的方法是如圖~

\(x(H(|\psi\rangle))=cos(\theta)\)
\(y(H(|\psi\rangle))=-sin(\theta)sin(\phi)\)
\(\left |\varphi \right |=tan^{-1}(\frac{-sin(\theta)sin(\phi)}{cos(\theta)})\)
\(\rightarrow \varphi=sgn(-sin(\theta)sin(\phi))tan^{-1}(\frac{-sin(\theta)sin(\phi)}{cos(\theta)})\)
(目前還在研究更正式的形式中...$^$)
如果使用正式方式的話,
就必須要解出下面的聯立方程式@~@
(好複雜 !~!
\(\left\{\begin{matrix}\frac{1}{\sqrt{2}} (cos(\theta)+sin(\theta)e^{i\phi})=cos(\theta ')e^{i\phi '}\\ \\\frac{1}{\sqrt{2}} (cos(\theta)-sin(\theta)e^{i\phi})=sin(\theta ')e^{i(\phi '+\delta ')}\end{matrix}\right.\)
(仍在解中...QwQ
Quantum computing實作!
-量子骰(ㄊㄡˊ)
(好饒口@~@還是叫ㄕㄞˇ子好了
因為我們還沒進入到多量子系統(這什?
所以沒辦法教 \(2\) 面以上的骰子。
不過先到這個網頁吧~
等等......還有一個很重要的觀念沒講呀?!
(請看下一頁\^~^/
不可回復的過程。
量子電腦之所以比古典電腦好,
就是因為它可以利用幺正變換將以往不可逆的傳統邏輯閘,改造為可逆的量子邏輯閘。
\(2\)個傳統\(Bit\)在經過\(And gate\)時會丟失信息,
而這也是讓系統熵增加並生熱的原因
並且無法找回被丟棄的信息。
在量子電腦中同樣有不可逆的過程,
而這個過程就是"測量\((Measurement)\)"。
有關測量
在實際測量量子狀態之前,
我們無法得知系統是處於哪種狀態量子狀態。
在測量之後,\(Qubit\)就會崩潰\((collapse)\)成單一的古典狀態。(\(0\) 或 \(1\))
這也代表,在測量之後,
我們就會只得到單一一個結果,
而不會同時得到兩個結果了。
Implement part . 1
點進去連結後,會看到要叫你登入
請點右邊的\(Google\)帳號登入鍵(一個\(G\)的)
登入之後,會看到以下畫面。

實作部分,請點選左邊的迴路。
可供任何人使用的量子電腦
進去選單之後,請點選上面的
\(New Circuit +\)
創造屬於自己的第一個量子迴路。
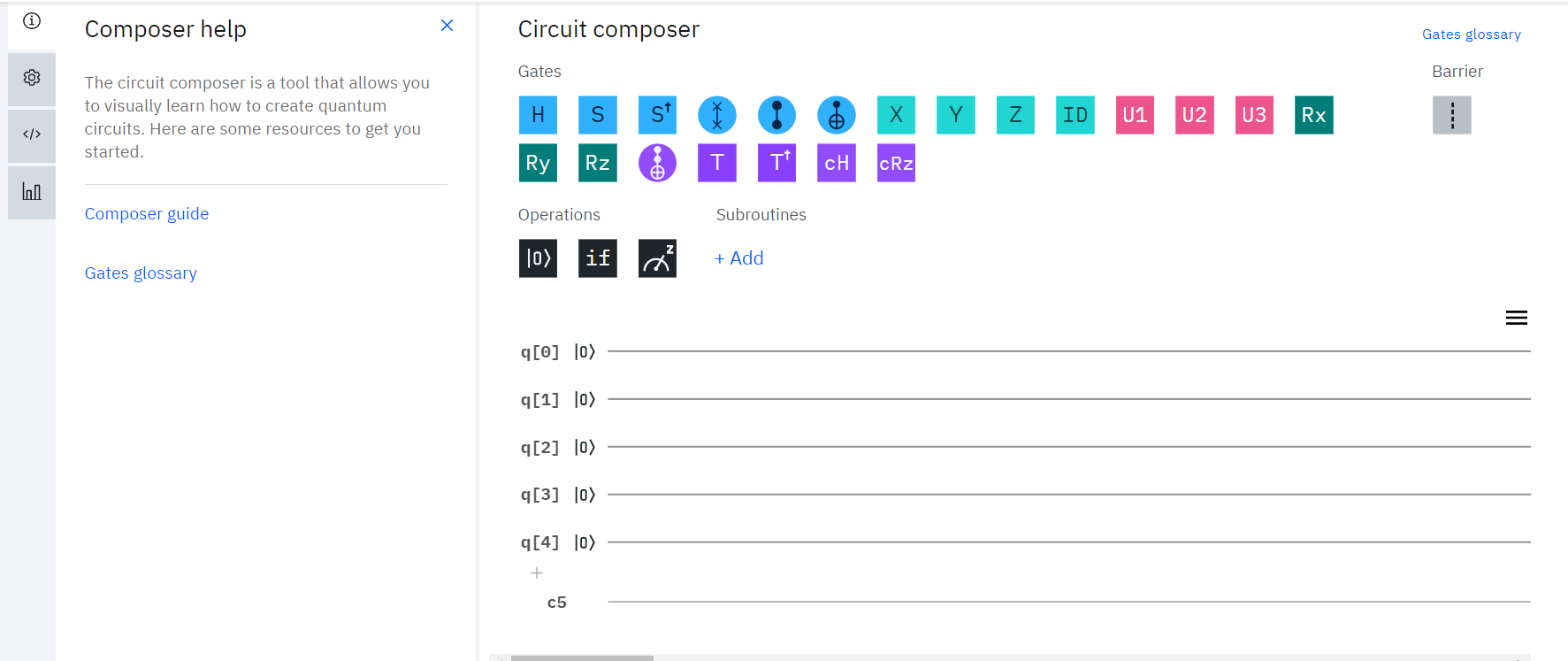
關於亂數,
大家應該知道在古典電腦上做出來的"亂數",
其實是"偽。亂數"
(只是使用了很複雜的亂數產生演算法,
但是在實質上仍然是假的)
但是在量子電腦上,
做出來的亂數確實是實實在在的"真。亂數"
(運用到疊加態Qubit的特性)
\(2\)面骰實作
繼剛才的教學之後,
我們知道要將一個 \(Qubit\) 變成
"觀察後有兩種結果"的話,
就必須要讓它進入 \(|+\rangle\) 的疊加態。

奇怪的骰子www\(\rightarrow\)
最後也要進行測量呦
不然就無法確定結果了@~@
所以,我們將一個 \(H gate\) 拖移到迴路上。
(讓\(|0\rangle\)經過這個 \(Gate\) 後變成\(|+\rangle\)的狀態
結果應該會是下面這樣。
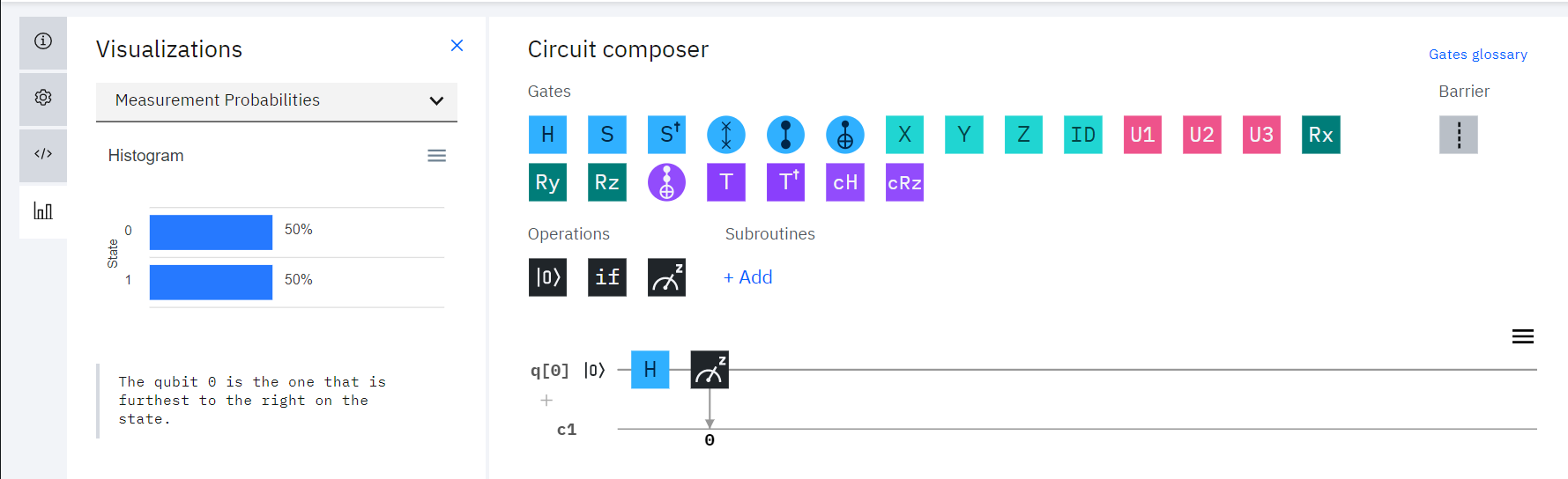
一半的機率是 \(|0\rangle\) ,一半是 \(|1\rangle\)。
但是其實這個只是模擬結果而已......>^<
到真正的量子電腦上執行時
仍然會有機率上的誤差。
(真正量子電腦實作篇請稍等...(_ _)
如果想要在真正的量子電腦上跑的話也可以 :
>>點右上方的儲存鍵
>>再點右方的 Run
>>選擇左邊沒有 "Simulator" 字眼的電腦)
>>再把右邊的 Shots 改成 1 (如果有需要的話)
接下來等它跑就可以了~^~^\\
Implement finished!
啥?!
也太少了吧?!
(因為還沒進入到多量子系統嘛~#^#
(等下就會介紹了。\^~^\
Basic concepts part.2
多量子系統
我們剛剛的教學,
都是屬於只操作單一\(Qubit\)的。
但是經過實做之後,
似乎好像沒辦法做出什麼好玩的東西呢(&^&)
所以接下來,
我們將學習如何結合多個量子的特性,
組合出單量子無法辦到的事情$^$
不過首先...<雙量子系統>
如果有一個量子是 \(|\varphi\rangle\),另一個是 \(|\phi\rangle\)
那麼它們兩個組合在一起就可以用
\(|\varphi\rangle \bigotimes |\phi\rangle\)
來表示。
\(\begin{bmatrix} a_{1} \\ a_{2} \end{bmatrix} \bigotimes \begin{bmatrix} b_{1} \\b_{2} \end{bmatrix} = \begin{bmatrix} a_{1}b_{1} \\a_{1}b_{2} \\a_{2}b_{1} \\a_{2}b_{2} \end{bmatrix}\)
這是它的矩陣形式
(有點像分配律(?
張量乘 \(\rightarrow\)
Practice!
如果今天我們 \(|+\rangle \bigotimes |1\rangle\)
那就是 \((\frac{|0\rangle + |1\rangle}{\sqrt{2}})(|1\rangle)\)
\(\rightarrow \frac{|01\rangle + |11\rangle}{\sqrt{2}}\)
(就是分配律的概念^~^
Gate 介紹
cX Gate (Controlled X Gate)
這個量子閘操作 \(2\) 個 \(Qubit\)
作用是 :
如果第一個 \(Qubit\) 為 \(|1\rangle\),
那麼就對第二個 \(Qubit\) 操作 \(X Gate\)。
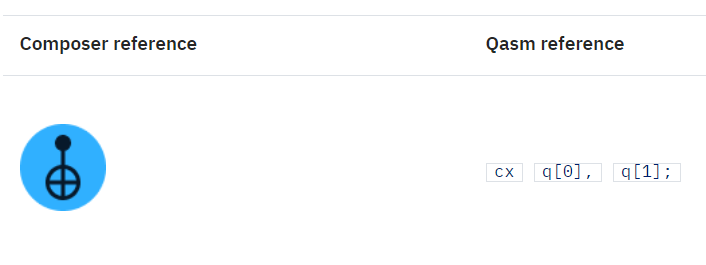
\(\leftarrow\) 第一個 \(Qubit\) (決定者)
\(\uparrow\) 第二個 \(Qubit\) (被操控者)
這是它的矩陣型態...(@^@)
\(\begin{bmatrix}1 & 0 & 0 & 0\\ 0 & 1 & 0 & 0\\ 0 & 0 & 0 & 1\\ 0 & 0 & 1 & 0\end{bmatrix}\)
要怎麼看這個矩陣呢?
- 5轉至矩陣
對兩個 \(Qubit\) 使用了 \(cX\ Gate\) 之後,
如果第一個 \(Qubit\) 是疊加態,
那麼這兩個 \(Qubit\) 就會"纏結"。
(又出現了奇怪的名詞QQ
神奇的<量子纏結>
剛剛有關 cX Gate 的部分,
將先使用數學表達式舉例說明 :
\(cX\left(\frac{|0\rangle + |1\rangle}{\sqrt{2}}, |0\rangle\right) = cX\left(\frac{|0, 0\rangle + |1, 0\rangle}{\sqrt{2}}\right) \rightarrow \frac{|00\rangle + |11\rangle}{\sqrt{2}}\)
(因為第一個 \(Qubit\) 為 \(|1\rangle\),
所以這個 \(Qubit\) 從 \(|0\rangle\) 變成 \(|1\rangle\) 了。
\((Quantum\ Entanglement)\)
所以......究竟是什麼 ?
量子糾纏是指,
當有 \(2\) 個或以上的 \(Qubit\) 糾纏時,
最後只要觀察其中一個,且不需要觀察其它
\(Qubit\) 的結果,就可以確定其他 \(Qubit\) 的結果了。
兩個 QS 不一定會是相反的呦 > <
要點
1. 糾纏的量子態,沒辦被寫成任兩個量子的結合。
(以剛剛的例子舉例)
\(\begin{bmatrix} ?\\?\end{bmatrix} \bigotimes \begin{bmatrix} ?\\? \end{bmatrix}\rightarrow \begin{bmatrix} \frac{1}{\sqrt{2}}\\0\\0\\\frac{1}{\sqrt{2}} \end{bmatrix}\)
2. 糾纏的量子態,無法以\(Bloch Sphere\) 表示,只能表示在 \(Qsphere\) 上。

\(\rightarrow\)
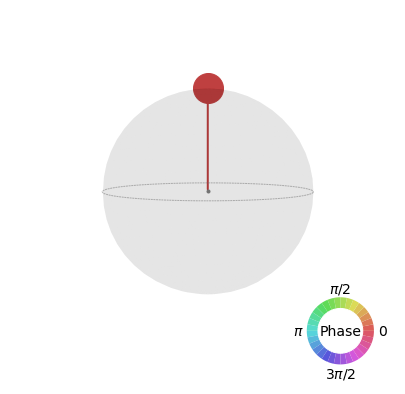
\(\bigcirc\)
( Qsphere 介紹篇一樣在準備中...(_ _)
Qsphere
- 可表示糾纏、疊加態
Gate 介紹

cH Gate (Controlled Hadamard Gate)
這個 \(Gate\) 的功能跟剛剛的 \(cX Gate\) 有些相似,只不過是對被操控的 \(Qubit\) 施加一個 \(H Gate\) 。(^~^)//
Practice !
請算出 \(cX(cH(|-\rangle, |1\rangle))\)
點它看解答&過程 \(\rightarrow\)
\((\frac{|0\rangle - |1\rangle}{\sqrt{2}})(|1\rangle) = \frac{|01\rangle - |11\rangle}{\sqrt{2}}\)
\(cH(\frac{|01\rangle - |11\rangle}{\sqrt{2}}) = \frac{|01\rangle - |1\rangle(\frac{|0\rangle - |1\rangle}{\sqrt{2}})}{\sqrt{2}} = \frac{\sqrt{2}|01\rangle - |10\rangle + |11\rangle}{2}\)
\(cX(\frac{\sqrt{2}|01\rangle - |10\rangle + |11\rangle}{2}) = \frac{\sqrt{2}|01\rangle - |11\rangle + |10\rangle}{2}\)
中間跳過了一大堆計算(&^&) \(\uparrow\)
終於要實作了(?
還沒www
在那之前,要先介紹 \(Ry Gate\) 的用法。
\(Ry Gate\) 是利用旋轉,將一個 \(Qubit\) 的量子態改變。
(簡單來說,就是可以讓一個狀態為 \(|0\rangle\) 或 \(|1\rangle\) 的 \(Qubit\) 進入疊加態。
從 \(|0\rangle\) 到疊加態
向量終於要派上用場了!
我們可以將一個向量型態的 QS
乘上一個矩陣,
就相當於讓這個 Qubit 經過這個量子閘。
所以,
我們先把 \(|0\rangle\) 乘上一個 Ry 的矩陣吧 !^!
數學的部分......@~@
\(\begin{bmatrix}cos(\frac{\psi}{2}) & -sin(\frac{\psi}{2})\\ sin(\frac{\psi}{2}) & cos(\frac{\psi}{2})\end{bmatrix}\begin{bmatrix}1\\0\end{bmatrix}\)
\(=\begin{bmatrix}cos(\frac{\psi}{2})\\ sin(\frac{\psi}{2})\end{bmatrix}\)
而 \(\left |\beta\right |^{2}\) (也就是 \(\left |sin(\frac{\psi}{2})\right |^{2}\)),
就會是 \(|1\rangle\) 的機率,
所以要解下列方程求出角 \(\psi\)~
\(sin^{2}(\frac{\psi}{2})=P(|1\rangle)\)
還是數學的部分......@~@
\(\rightarrow sin(\frac{\psi}{2})=\sqrt{P(|1\rangle)}\)
\(sin^{2}(\frac{\psi}{2})=P(|1\rangle)\)
\(\rightarrow \frac{\psi}{2}=sin^{-1}(\sqrt{P(|1\rangle)})\)
\(\rightarrow \psi=2sin^{-1}(\sqrt{P(|1\rangle)})\)
反三角函數
所以可知,
如果想要把一個為 \(|0\rangle\) 的 QS
加上 \(Ry\ Gate\) 變成有 \(P\) 的機率是 \(|1\rangle\) 的話,
要選轉的角度就是下列呦~^~^//
\(\psi=2sin^{-1}(\sqrt{P})\)
(等等會直接拿來用^^~)
久違的實作,
請看下一章。
Implement part . 2
\((Final)\)
3面骰實作
學過多量子系統後,我們終於可以實作 \(3\) 面骰了!
不過首先,我們要把我們的目標列出 :
\(|00\rangle \rightarrow \frac{|00\rangle + |01\rangle + |10\rangle}{\sqrt{3}}\)
目標:經過對各個量子操作量子閘後,
將左邊的基本態變成右邊的狀態。
首先...<觀察>
\(|00\rangle \rightarrow \frac{|00\rangle + |01\rangle + |10\rangle}{\sqrt{3}}\)
我們首先觀察左邊的 \(Qubit\),
從最一開始全為 \(|0\rangle\), 變成有 \(\frac{1}{3}\) 的機率為 \(|1\rangle\) 了。
為此,我們不行使用 \(H Gate\) 進行操作,
(因為不是 \(\frac{1}{2}\) 的機率)
而是要使用新學的 \(Ry Gate\) 來操作。
<設計Part.1>
利用剛才所學
我們直接將 QS 為 \(|0\rangle\) 的 Qubit
通過下列的 Ry Gate 吧 !^!
\(Ry(2sin^{-1}(\sqrt{\frac{1}{3}}),\ 1)\)
為什麼是 1 ?
\(Ry(2sin^{-1}(\sqrt{\frac{1}{3}}), 1)\)
如剛剛所看到的,
在這個式子的後面多出了一個 1 :
\(\bigcirc\)
此為要進行操控的 \(Qubit \uparrow\)
這是因為依照順序的關係
\(Qubit\) 的順序,通常是以下列方式表現:
\(|0\rangle_{0}\)
\(|0\rangle_{1}\)
\(...\)
\(|0\rangle_{n-1}\)
\(|0_{n-1}\;0_{n-2}\;...\;0_{1}\;0_{0}\rangle\)
第1個
第2個
第n個
...
\(|0\rangle_{n-2}\)
第n-1個
因此,剛剛的 \(1\) 表示的是第二個 \(Qubit\)。
\(\rightarrow\)
數學式Part.1
我們將剛剛進行的操作寫成數學式,並將經過第一步驟後兩個 \(Qubit\) 的量子態令為 \(|\varphi_{2}\rangle_{1}\)
\(Ry(2sin^{-1}(\sqrt{\frac{1}{3}}), 1)|00\rangle \rightarrow \frac{\sqrt{2}|00\rangle + |10\rangle}{\sqrt{3}} = |\varphi_{2}\rangle_{1}\)
再與目標進行比對。
\(|00\rangle \rightarrow \frac{|00\rangle + |01\rangle + |10\rangle}{\sqrt{3}}\)
會發現,第一個 \(Qubit\) 如果為 \(|0\rangle\) 時,第二個 \(Qubit\) 應該要有一半的機率為 \(|0\rangle\),一半的機率為 \(|1\rangle\)。
\(\bigcirc\)
\(\bigcirc\)
<設計Part.2>
因此,我們使用 \(cH Gate\) 將條件設為
"當第一個 \(Qubit\) 為 \(|0\rangle\)",
就對第二個 \(Qubit\) 執行 \(H Gate\)。
但是,\(cH Gate\) 只能適用於偵測
"是否為 \(|1\rangle\)" 的條件,因此要先將第一個 \(Qubit\) 利用 \(X Gate\) 反轉,偵測後,再次反轉回原本的樣子。
\(X(1)(|\varphi_{2}\rangle_{1}) \rightarrow cH(|\varphi_{2}\rangle_{1}, 1, 0) \rightarrow X(1)(|\varphi_{2}\rangle_{1})\)
條件位元\(\uparrow\)
\(\uparrow\)被操控位元
數學式Part.2
我們將剛剛進行的操作寫成數學式
\(X(1)(|\varphi_{2}\rangle_{1}) \rightarrow \)
\(\frac{\sqrt{2}|10\rangle + |00\rangle}{\sqrt{3}}\)
\(cH(\frac{\sqrt{2}|10\rangle + |00\rangle}{\sqrt{3}}, 1, 0) \rightarrow\)
\(\frac{\sqrt{2}|1\rangle(\frac{|0\rangle + |1\rangle}{\sqrt{2}}) + |00\rangle}{\sqrt{3}} = \frac{|10\rangle + |11\rangle + |00\rangle}{\sqrt{3}}\)
\(X(1)(\frac{|10\rangle + |11\rangle + |00\rangle}{\sqrt{3}}) \rightarrow \)
\(\frac{|00\rangle + |01\rangle + |10\rangle}{\sqrt{3}}\)
實作迴路
結果應該會是下面這樣:
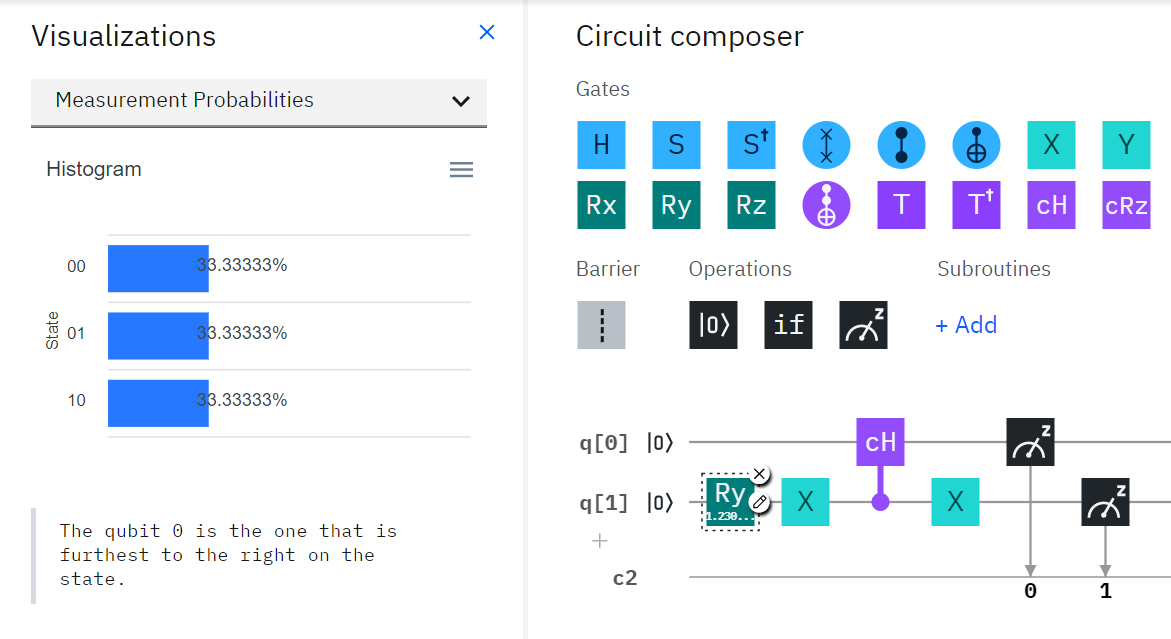
步驟一
步驟二
最後一定要進行測量呦> <
恭喜 !
實作完成。
這次的小小
Quantum Computing 教學
就到此告一段落。
感謝專心聆聽的各位\(^~^)/
{Quantum Computing}
- fin. (?
Quantum Dice!
<Extra Chapter>
目前是放對量子骰發現的規律
和相關的咚咚 \\(&^&)//
實作邏輯
與資訊提取
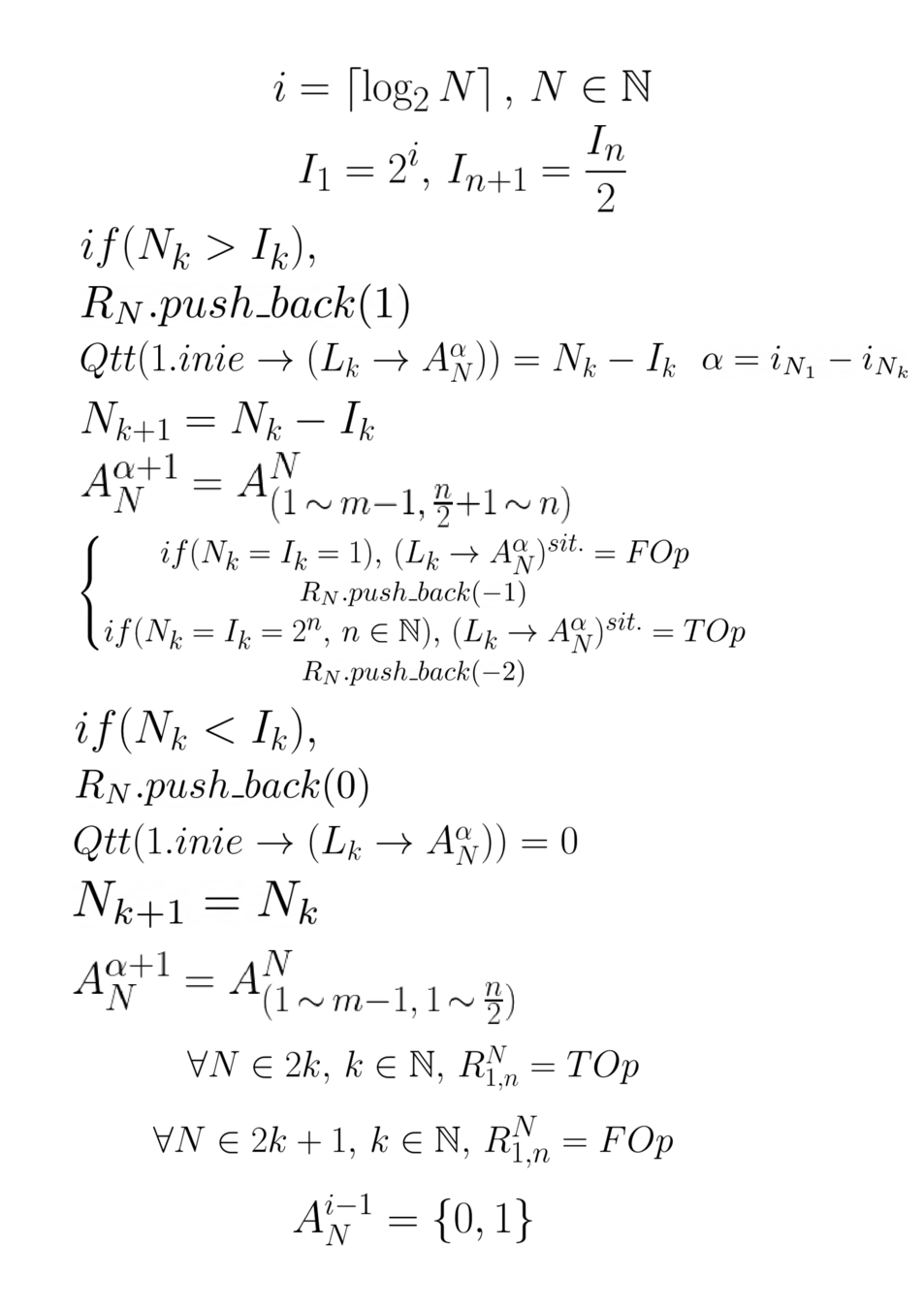
數學式展開通式
\(|0\rangle^{i} \rightarrow \frac{1}{\sqrt{N}}\sum_{i=1}^{L}(|i_{2}\rangle)\)
\(=\sum_{m=1}^{L}\left |A_{m}\right |(\sqrt{\frac{I_{m}}{N}}|<c>\sum_{n=1}^{m-1}(A_{n})0+^{\log_{2}{I_{m}}}\rangle)\)
\(=\frac{1}{\sqrt{N}}\sum_{m=1}^{L}\left |A_{m}\right |(\sqrt{I_{m}}|(<c>\sum_{n=1}^{m-1}A_{n})0+^{\log_{2}{I_{m}}}\rangle)\)
\(\left \{ A_{k} \right \}=sgn(sgn(N_{k}-I_{k})-\frac{1}{2})\)
\(\left \{ I_{k} \right \}=2^{i-k}\)
\(L=n(A)=n(I)\)
\(N\neq 2^{p},\ p, k\in\mathbb{N}\)
還有可以寫量子骰程式的程式(?^?
(利用上面那張密密麻麻的就可以做出來了\\^~^\
(但是還沒證明完(_ _))
Quantum Algorithm
<Hidden Chapter>
小小的隱藏章節\^~^/
在這個章節,
我們要來介紹最一開始時影片中
的兩個量子演算法。
演算法No.1:
大家或許有聽過現在被頻繁使用的
RSA加密演算法,
它的基本概念,
就是使用兩個質數進行相乘,
\((p_{1})(p_{2})=N\)
要解密的話,
就必須在不知道 \(p_{1},\;p_{2}\) 的狀況下,
找出 \(N\) 是由哪兩個質數相乘。
\(143 = (?_{1})(?_{2})\)
\(143 = (11)(13)\)
這還好嘛~ (?
那這個呢?
\(106,913,299,109 = (?_{1})(?_{2})\)
\(106,913,299,109 = (9,369,319)(11,411)\)
而且在真實加密中,
\(N\) 都有可能長達幾千位,
現代的電腦需要花費
很多
很多
很多
很多
很多
很多
很多
很多
很多
很多
很多
很多
很多
很多
很多
很多
很多
很多
的時間才可以解碼完成。
(&~&)