Patrick Power

Instrumental LLMS

Quote to Ponder

The key facts of his career, which are that he knew (1) a lot about math and (2) nothing about finance. This seems to have been a very fruitful combination. If you can program computers to analyze data with, as it were, an open mind, they will pick out signals from the data that work, and then you can trade on those signals and make an enormous fortune. If you insist on the signals making sense to you, you will just get in the way.

Matt Levine (Bloomberg)

Overview

Overview

\tilde{Y}_i \perp D_i \vert X_i

In much of applied micro work, Causal Inference rests on the following condition

In many settings (Health Care, Education, Housing) we have the underlying text

For a refresher on the basics of casual inference, please see these slides

(2) Illustrate that LLMs may particularly advantageous IV

Aim(s)

(1) Clarify the conditional independence assumption for text based controls

Motivation

Motivation #-1

There are a lot of good reasons for not wanting to use LLMs for Causal Inference

  • Black Box Estimators
  • Have Biases
  • Expensive to Fine-tune
  • Harder to fit than linear models
  • Hallucinate

Motivation #1 (Identification)

  • There is tremendous variation across individuals 
  • Language Models -- via the attention mechanism -- can account for this level of detail
  • We often would like to "control" for these differences using a rich set of control variables
  • Eduction
  • Skills
  • Emotional well-being
  • Faith
  • Finances
  • Health
  • Hope
  • Social Skills

Variables Taken From: Evans et al (2024)

Motivation #2 (Efficiency)

In instrumental variables, there can be an exponential relationship between the average first stage and the variance of the LATE estimator

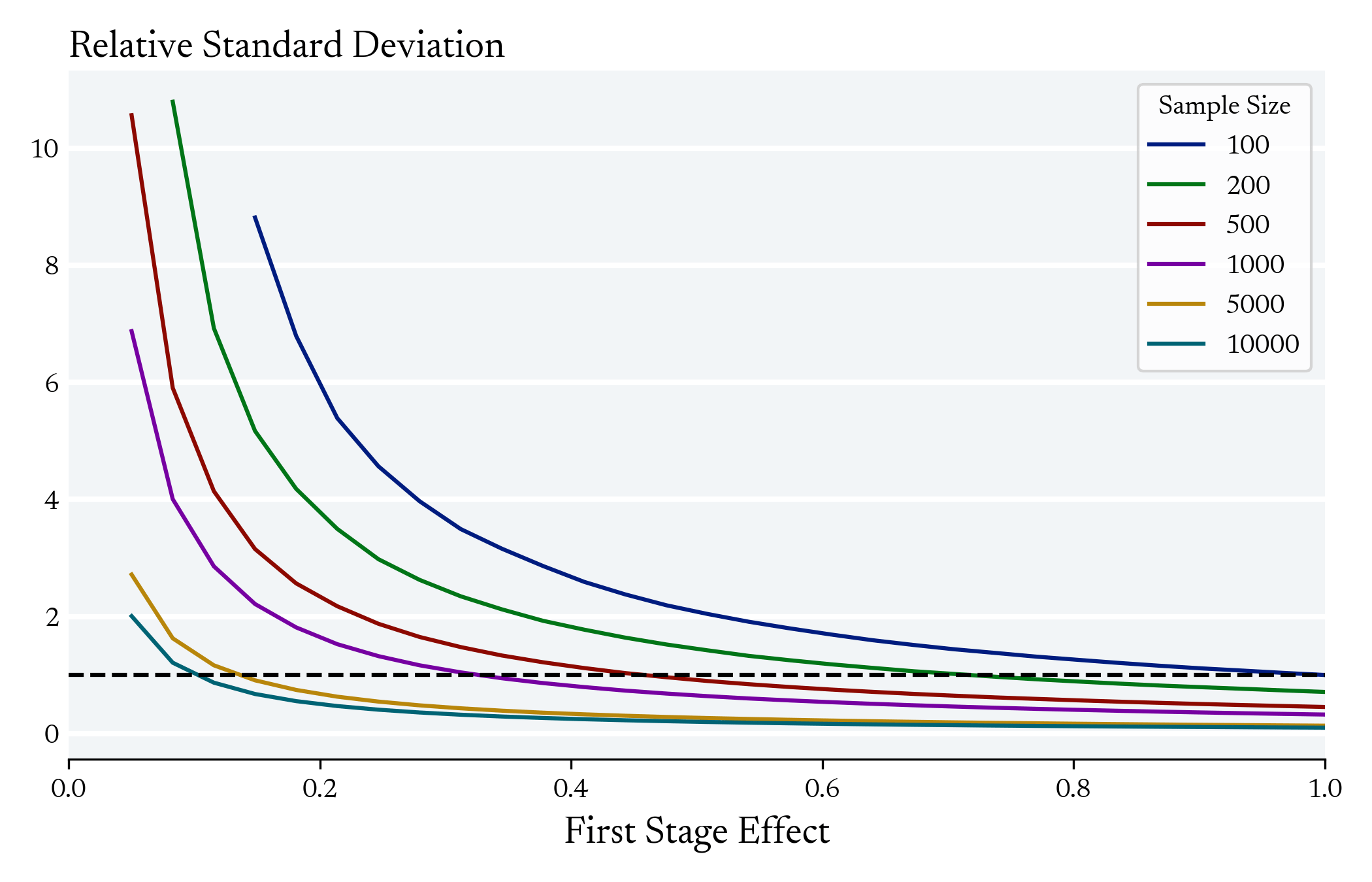
Many Applied Microecon papers Exist in this range

But maybe there is "partial" information about who is a complier that language models can exploit in the first stage to reduce the variance

Motivation #2 (Efficiency)

Practitioners are often concerned about high take-up rates and therefore screen out individuals from the study

"We designed the consent and enrollment process for this RCT to yield high take-up rates, screening potential clients on their willingness to participate. In fact, about 91 percent of those in the treatment group who were offered services actually completed the initial assessment and received some services"

But you don't need to screen these individuals out before hand

Motivation #3 (Tranparency)

  • One motivation for using linear models is that the reported estimate is a function of the data
  • For non-linear models, the estimate is a function of the data and several hyperparameters - nodes, depth, learning rate schedule, activation function, etc.
  • In-context learning (via a prompt) can allow us to fit non-linear models without hyperparameters

Large Language Models

The Fundamental Challenge

The Product Topology Breaks Down

"You shall know a word by the company that it keeps" Firth [1957]

(\mathcal{V}, \mathcal{T}_{\mathcal{V}})
(\mathcal{V}^{d}, \quad \quad \quad \quad ? \quad \quad \quad \quad )

Words (Tokens)

(\mathcal{R}, \mathcal{T}_{\mathcal{R}})
(\mathcal{R}^d, \mathcal{T}_{\mathcal{R}}\times \mathcal{T}_{\mathcal{R}} \times \dots \times \mathcal{T}_{\mathcal{R}})

The Real Numbers

Current Challenges in the literature (Memory, and Attention Scaling: A Mamba Primer)

What Language Model Should We Use?

  • Encoder v.s Decoder?
  • Model Size?
  • Learning Rate?
  • If Decoder
  • Chat Template?
  • Classification Head?
  • Qlora?

LLMs

f_{\theta}(x) = \sum _j \alpha_{j, \theta} 1_{A_{j, \theta}(x)}
f^*_{int} = \textrm{arg} \underset{f \in \mathcal{H}}{\textrm{min}} \| f \| \quad \forall i f(x_i) = y_i

Identification

Estimator

Project Data onto Low-Dimensional Manifold and Average locally

Maybe? But also latent

Estimator

Project Data onto Low-Dimensional Manifold and Average locally*

Probably Not Exactly True

Identification

\tilde{Y}_i \perp D_i \vert X_i

Probably Not Exactly True

*Even linear models extrapolate

Causal Inference Doesn't Really Work

x \longmapsto \mathbb{E}[Y \vert X](x)

Conditional Expectation Function

\mathbb{E}[Y_i \vert D_i =1, X_i] \overset{a.s.}{=} \mathbb{E}[\tilde{Y}_i(1) \vert X_i]

When the treatment variable is conditional independent of the potential outcomes, the following holds

(1)
f_{\theta}(x) \approx \mathbb{E}[\tilde{Y}_i(1) \vert X_i]

We approximate the Condition Expectation function via a parameterized model

(2)

In applied micro, the typical model is

\theta ^T x \approx \mathbb{E}[\tilde{Y}_i(1) \vert X_i]
(3)

Framework

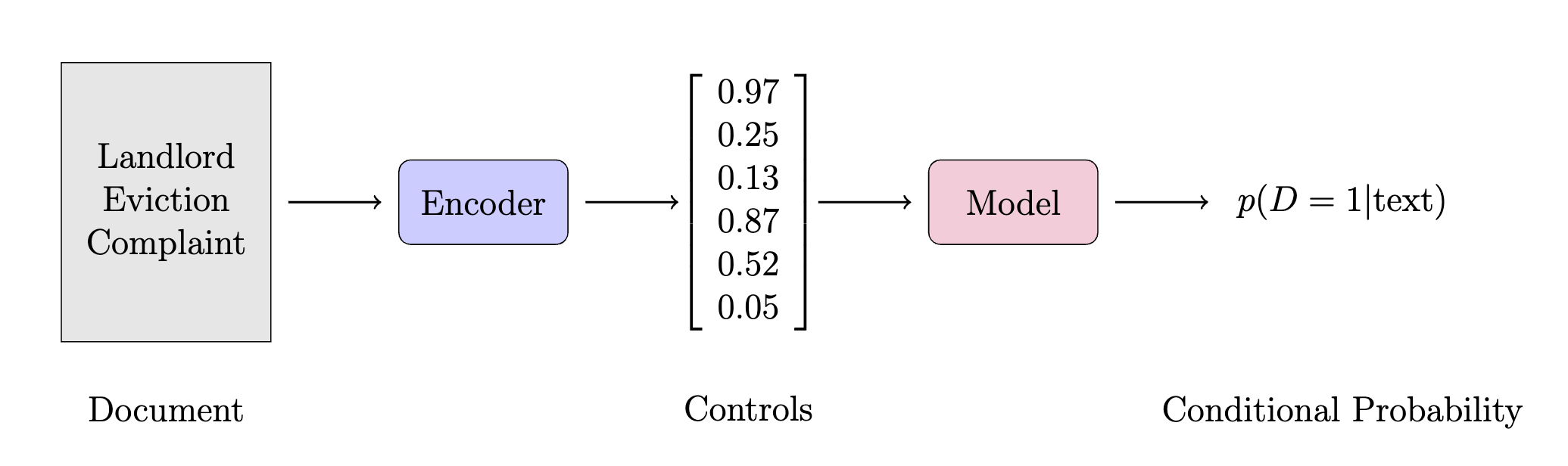
In the standard Applied Micro Setup

Encoder: Hand Selected Features

Model: Linear function of the control variables

Topology provides necessary structure for Conditional Independence

\tilde{Y}_i \perp D_i \vert X_i
\implies \mathbb{E}[\tilde{Y}_iD_i \vert X_i] = \mathbb{E}[\tilde{Y}_i\vert X_i]\mathbb{E}[D_i\vert X_i]

The conditional expectation function defined with respect to the Borel sigma algebra generated with respect to the topology on X products out

Adding Controls

g : \Omega \to \mathcal{R}^2
\omega \longmapsto (g_1(\omega), g_2(\omega))
\big( \Omega, \mathcal{T}_g\big)

More functions are continuous under the finer topology

Creates a "finer" topology on the underlying set

f : \Omega \to \mathcal{R}^3
\omega \longmapsto (g_1(\omega), g_2(\omega), f_3(\omega))
\big( \Omega, \mathcal{T}_f\big)
\mathbb{E}[Y_i\vert D_i , X_i]

A finer topology places fewer restrictions on the Conditional Expectation Function

A finer topology also places fewer restrictions over our continuous model

f_{\theta}(D_i, X_i)

A continuous function exploits meaningful variation

\textrm{Var}(Y_i) = \mathbb{E}[\textrm{Var}(Y_i \vert X_i)] + \textrm{Var}(\mathbb{E}[Y_i \vert X_i])

Unlike Homeomorphisms, continuous functions do not preserve all topological properties, but they do preserve the notion of "closeness"

Causal Framework

Conditional Independence

\big( X, \mathcal{T}\big)

Model

\big( X, \Tau, \langle \cdot, \cdot \rangle \big)

Large Language Model

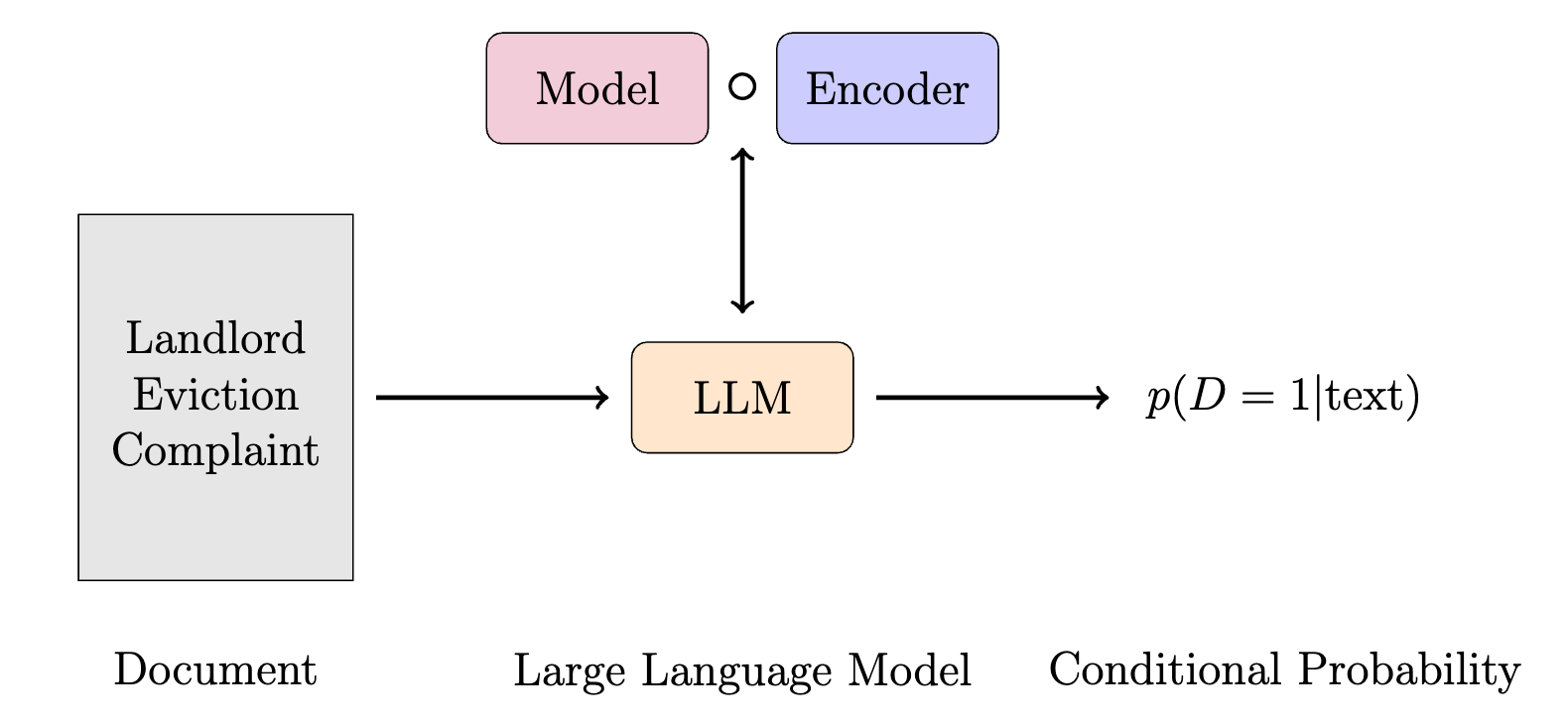
  • We cannot "directly" influence the topology, so we use the discrete topology
  • The model and encoder are not exposed separately

Causal Inference

We define the following random variables of interest

X_i : \Omega _n \to L^V \ (\textrm{Finite sequences of tokens})
D_i : \Omega _n \to \{0,1\}
\tilde{Y}_i : \Omega _n \to \{0,1\} \to \{0, 1\}
\Big( \Omega_n, \mathcal{F}_n, \mathbb{P}_n\Big)

We begin with the underlying probability space

For notational simplicity, we take the treatment and outcome variables to be binary valued

Causal Inference

\forall A, B, C \in \sigma(\tilde{Y}_i), \sigma({D}_i), \sigma (X_i), \int 1_{A \cap B} d\mathbb{P}_C = \int 1_{A} d\mathbb{P}_C \int 1_{B} d\mathbb{P}_C

Conditional Independence

\int _{\Omega} \mathbb{E}[\tilde{Y}_i(1) - \tilde{Y}_i(0)]d\mathbb{P} = \int _{\Omega _n} \mathbb{E}[Y_i \vert D_i=1, X_i] - \mathbb{E}[Y_i \vert D_i=0, X_i] d\mathbb{P}_n

Identification

\textrm{Population Probability Space}\ := \Big( \Omega, \mathcal{F}, \mathbb{P}\Big)

We avoid the idea of "Observed Population" (Lewbel [2019]) which is conceptually a bit fuzzy when working with clustered data and focus instead on the underlying DGP

High Level Summary

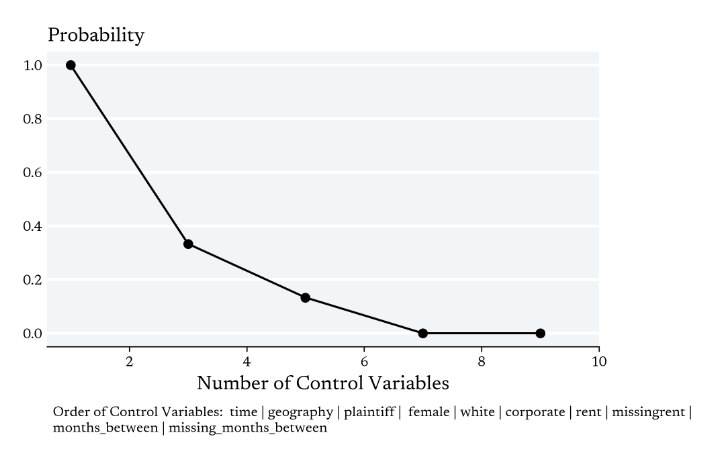
Right to Counsel

We're already Extrapolating with 'Vector' Data

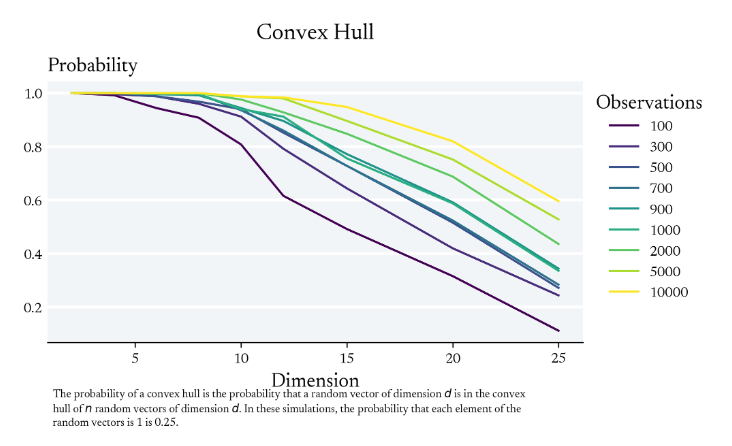
Simulation

Motivation #2

What notion of similarity are we using to define Conditional Independence?

(1)

What notion of similarity are we using to form predictions from the training data?

(2)

Big Picture Overview

Undergraduate courses on Econometrics can be difficult to follow because they don't differentiate between these two notions of similarity

The Aim of this paper is to act as additional chapter of Mostly Harmless Econometrics focused on LLMs

The Mostly Harmless Econometric Approach is arguably more intuitive because it distinguishes between the two

  • Reason about the CEF
  • Approximate it with a linear model

Efficiency

Revisiting Controls

Language models can exploit features of the text which differentiate between these subpopulations and therefore "improve" estimation of IV parameters

Claim

  • Including controls which allow us to differentiate between Always Takers/ Never Takes/ Compliers

(1) Doesn't change the first stage estimate

(2) Can decrease the variance of the LATE estimate

  • The primary motivation for controls is identification
\tilde{Y}_i \perp Z_i \vert X_i
\tilde{D}_i \perp Z_i \vert X_i

Motivational Example

Landlord Complaint

  • Tenant evicted for selling drugs
  • Tenant evicted for a conflict which resulted in a fatality
  • Tenant uses Section 8 Housing Voucher
  • Tenant failed to pay rent because in hospital

Examples

We observe aspects of the case which are potentially informative about who we receive legal representation if offered 

\mathbb{E}[D_i \vert X_i, Z_i]
\tilde{D}_i \perp Z_i

Instrument Randomly Assigned

Models

Standard

\mathbb{E}[D_i \vert Z_i]

Exploiting Heterogeneity

\mathbb{E}[D_i \vert X_{i1}, Z_i]

Exploiting Heterogeneity in the First Stage can Increase the Variance of Individual Level Predictions

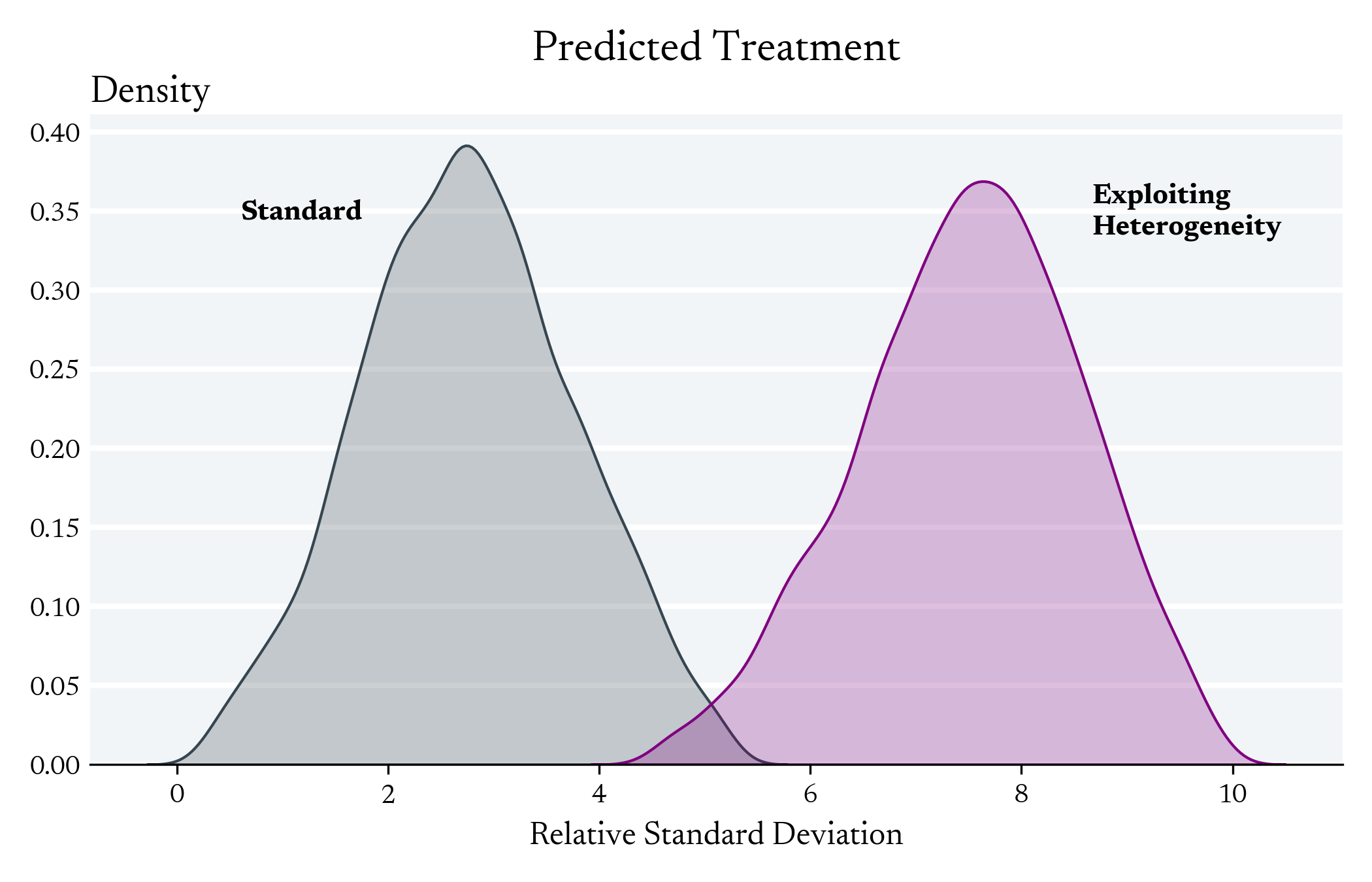
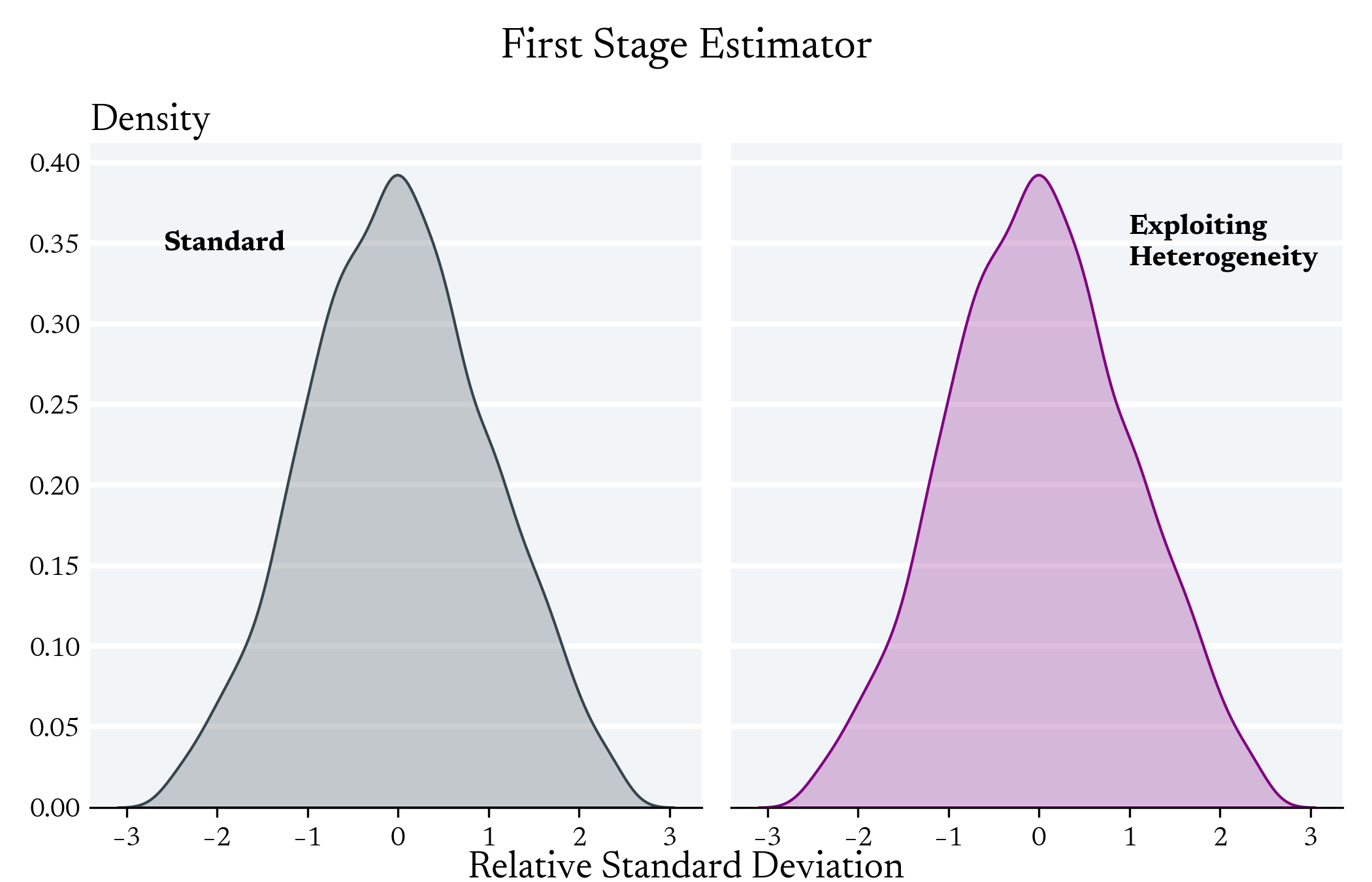
First Stage Effect

We don't expect to see differences between these models with regards to the Average First Stage Effect

\textrm{Var}\Big(\hat{\mathbb{E}}[D_i \vert Z_i =1] - \hat{\mathbb{E}}[D_i \vert Z_i =0]\Big)
\textrm{Var}\Big(\int \hat{\mathbb{E}}[D_i \vert X_i, Z_i =1] - \hat{\mathbb{E}}[D_i \vert X_i, Z_i =0] \hat{\mathbb{P}}_X\Big)
\approx

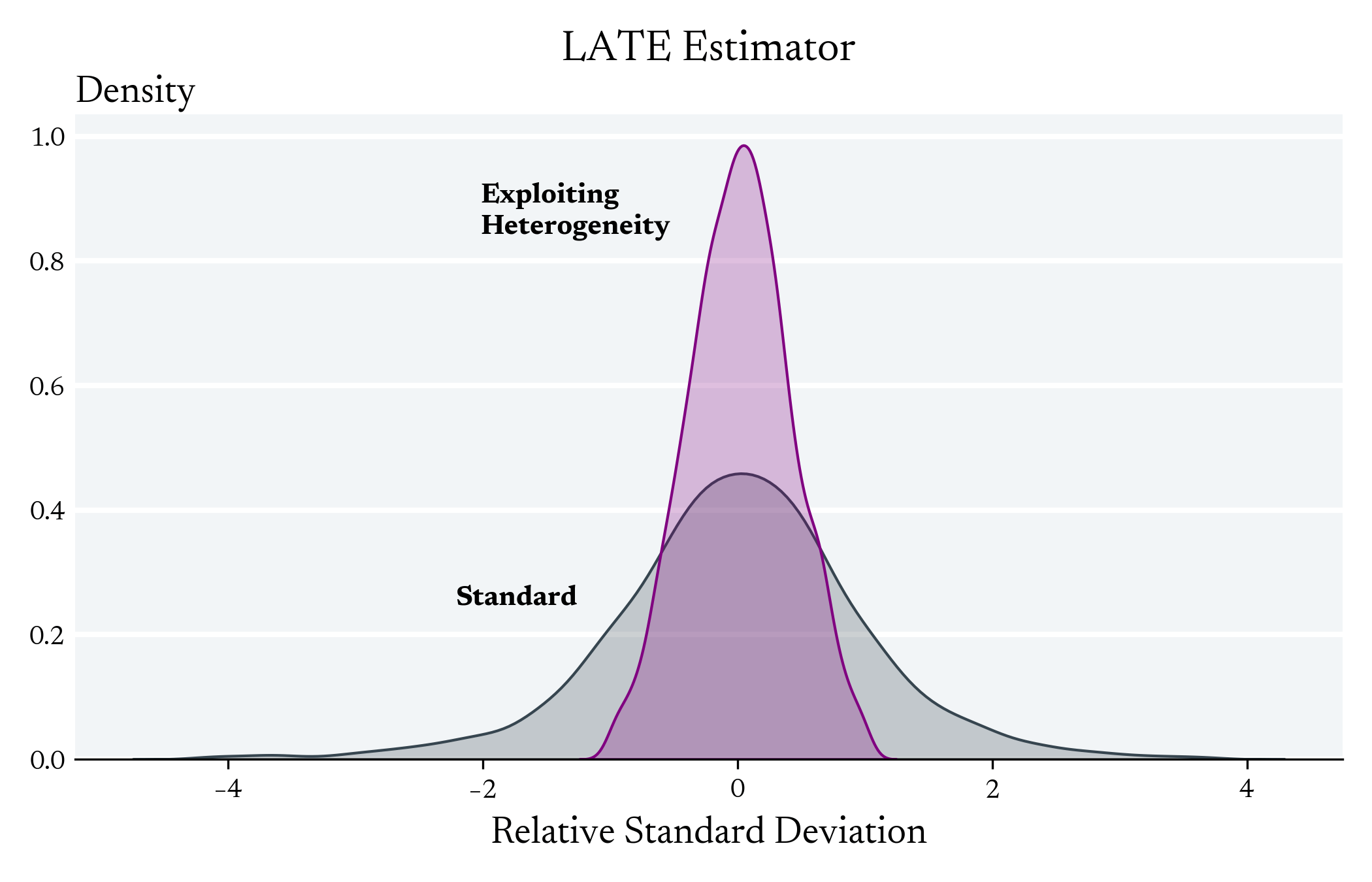
Exploiting Heterogeneity in the First Stage can Decrease the Variance the LATE Estimator

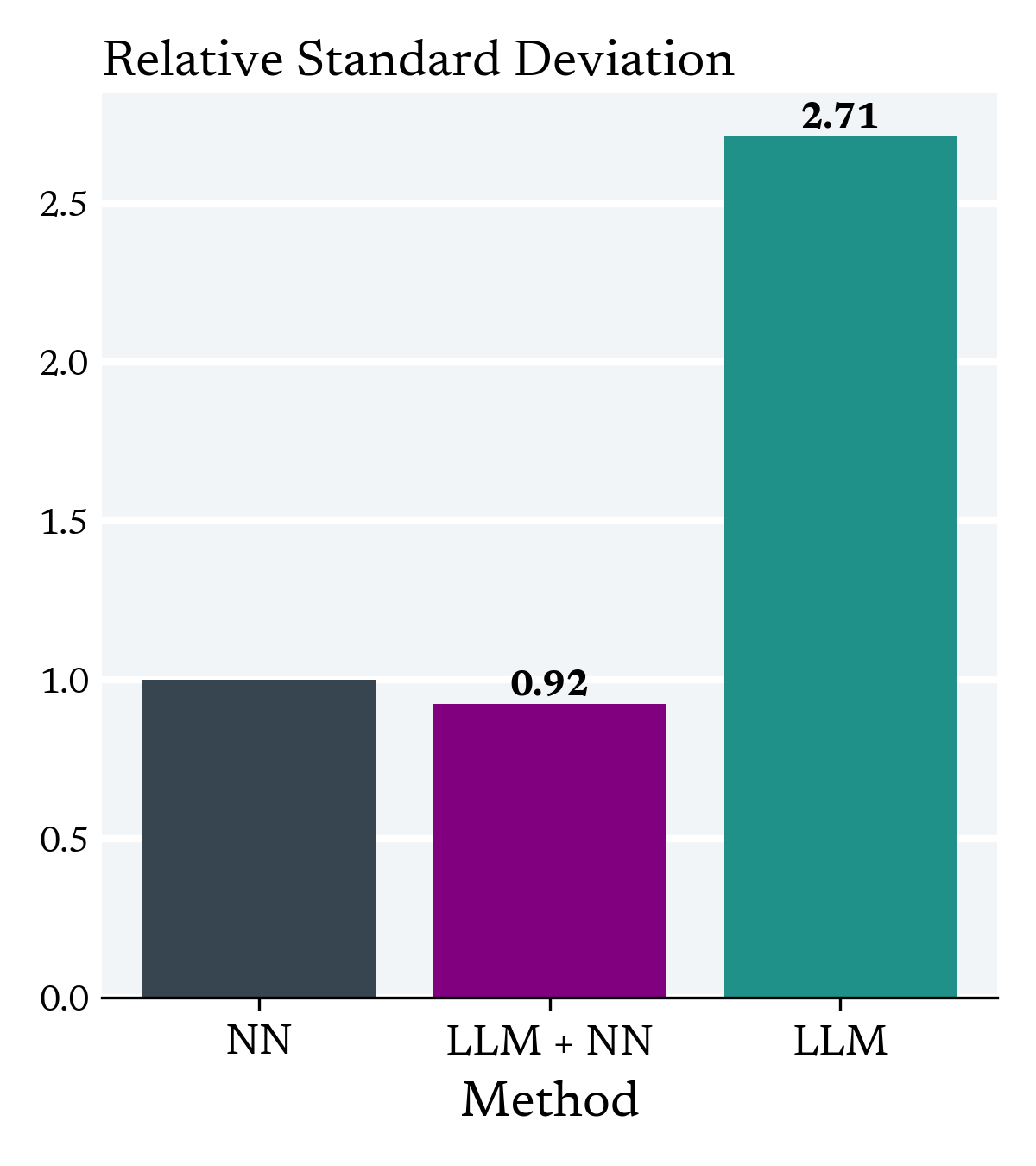
Simulation # 1

IV Simulation

(1)

Sample Numerical Features

x = [x_1, x_2, x_3, \dots, x_4]

(2)

Map Numerical Features to Text

via prompt

x \longmapsto t^*(x)

(3)

Define First Stage Function

x,z \longmapsto z*x_4

(4)

(0)

Binary Instrument is Randomly Assigned

\textrm{Treat}\ x_4 \textrm{ as a variable that researchers don't control for}

For computational reasons, we choose a simple first stage function so that we can learn it with relatively few observations

Simulation # 2

Context: Instrumental Variables with Preferential Treatment

  • The offer of legal representation is conditionally randomly assigned
  • Treatment is prioritized to tenants with certain characteristics
\textrm{Instrument} := \textrm{Zip}_i + \textrm{Prioritized to vulnerable tenants}

Not clear how to make this work with a linear model

***For example, in Connecticut's rollout of the Right to Counsel, legal aid was offered in some zip codes initially but not others, and within these zip codes legal aid was prioritized to tenants who were more vulnerable

"The success of machine learning algorithms generally depends on data representation, and we hypothesize that this is because different representations can entangle and hide more or less the different explanatory factors of variation behind the data"

Representation Learning

Bengio et al. (2014)

"The performance of machine learning methods is heavily dependent on the choice of data representation (or features) on which they are applied. For that reason, much of the actual effort in deploying machine learning algorithms goes into the design of preprocessing pipelines and data transformations that result in a representation of the data that can support effective machine learning"

Residualized Framework

Selection-on-Observables

Partially Linear Models

Y_i = \beta_1(\underbrace{D_i - \mathbb{E}[D_i \vert X_i]}) + \eta_i

The difference between treatment and the predicted treatment based only on the controls

Linear Models

Y_i = \alpha + \beta_1 D_i + \beta_2^T X_i + \varepsilon_i
Y_i = \beta_1(D_i - \hat{D}_i) + \eta_i
\hat{D}_i = \hat{\gamma}_1 + \hat{\gamma}_2X_i

Instrumental Variables

Y_i = \alpha + \beta_1 \hat{D}_i + \beta_2 X_i + \varepsilon_i
D_i = \gamma_0 + \gamma_1 X_i + \gamma_2 Z_i + \varepsilon_i

Linear IV

Y_i = \beta_1(\hat{D}_i - \bar{\hat{D}}_i) + \eta_i
\bar{\hat{D}}_i = \hat{\phi}_1 + \hat{\phi}_2X_i

Partially Linear IV

Y_i = \beta_1(\mathbb{E}[D_i \vert X_i, Z_i] - \mathbb{E}[D_i \vert X_i]) + \eta_i