HW4!!!
b05902031謝議霆
b05902008王行健
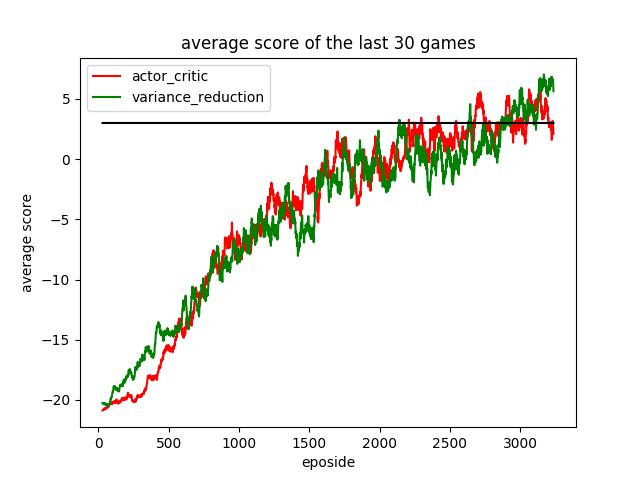
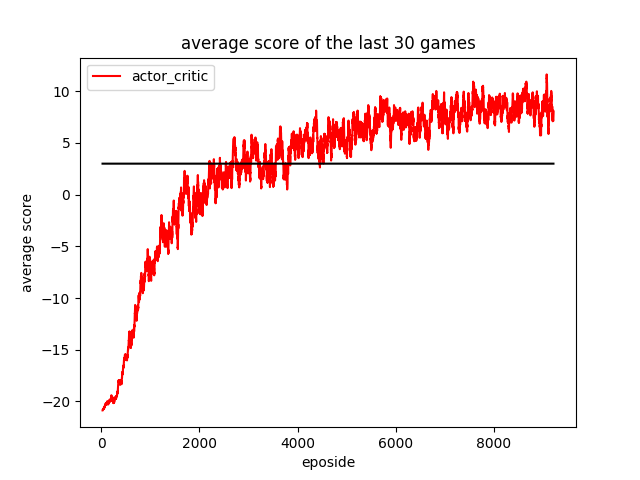
Actor critic VS Policy gradient
Actor critic
Actor critic VS Policy gradient
Algorithm
1. Play a episode with fixed model and get the reward
- for each state, get (probability, reward)
2. reward = reward * r ^ (t' - t) - baseline
3. ▽J = ▽log(probability) * reward
4. update with ▽J
5. repeat to 1.



Agent at different episode
200 episode
1200 episode
2500 episode
Title Text
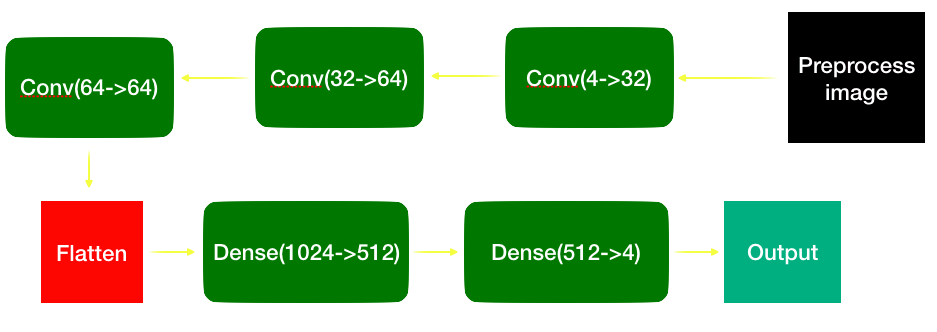
Model
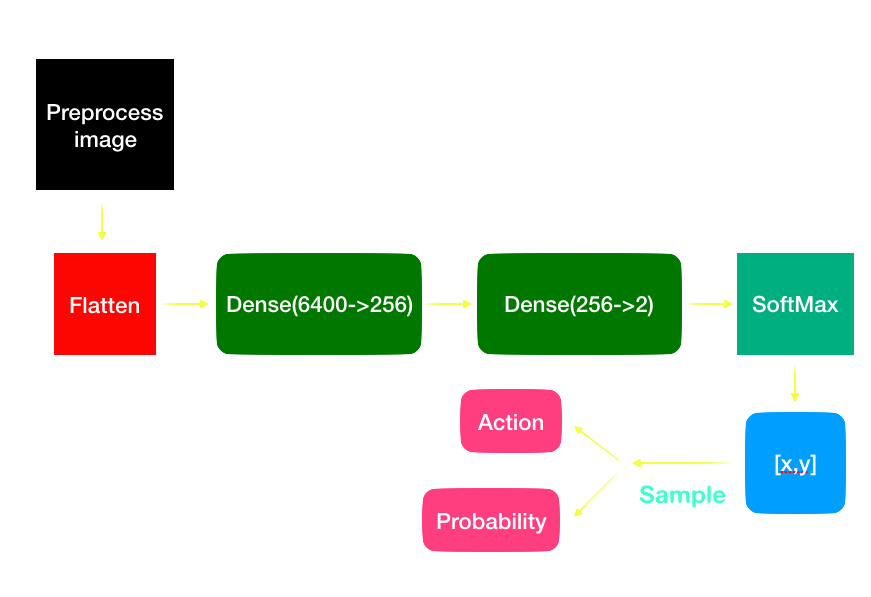
1. Play a episode with fixed model and get the reward
- for each state, get (probability, reward)
2. reward = reward * r ^ (t' - t) - baseline
3. ▽J = ▽log(probability) * reward
4. update with ▽J
5. repeat to 1.
Reward
1. Play a episode with fixed model and get the reward
- for each state, get (probability, reward)
2. reward = reward * r ^ (t' - t) - baseline
3. ▽J = ▽log(probability) * reward
4. update with ▽J
5. repeat to 1.
| state | 0 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|---|
| reward | 0 | 0 | 0 | 0 | 0 | -1 |
| modified | -0.99^5 | -0.99^4 | -0.99^3 | -0.99^2 | -0.99 | -1 |
| state | 0 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|---|
| reward | 0 | 0 | 0 | 0 | 0 | 1 |
| modified | 0.99^5 | 0.99^4 | 0.99^3 | 0.99^2 | 0.99 | 1 |
Issue
- Winning all the time
- Is it possible to hit every ball?
- Change the reward with the hitting
- Rule-based
- Will model learn such method?
- True baseline set by TA's
- How to?

Reward-baseline
1. Play a episode with fixed model and get the reward
- for each state, get (probability, reward)
2. reward = reward * r ^ (t' - t) - baseline
3. ▽J = ▽log(probability) * reward
4. update with ▽J
5. repeat to 1.
| state | 0 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|---|
| reward | 0 | 0 | 0 | 0 | 0 | 1 |
| modified | 0.99^5 | 0.99^4 | 0.99^3 | 0.99^2 | 0.99 | 1 |
| normalize | -1.4540 | -0.8802 | -0.3006 | 0.2849 | 0.8763 | 1.4736 |
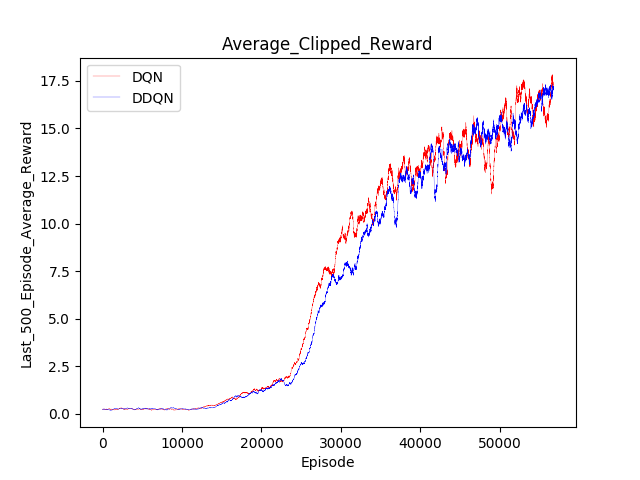
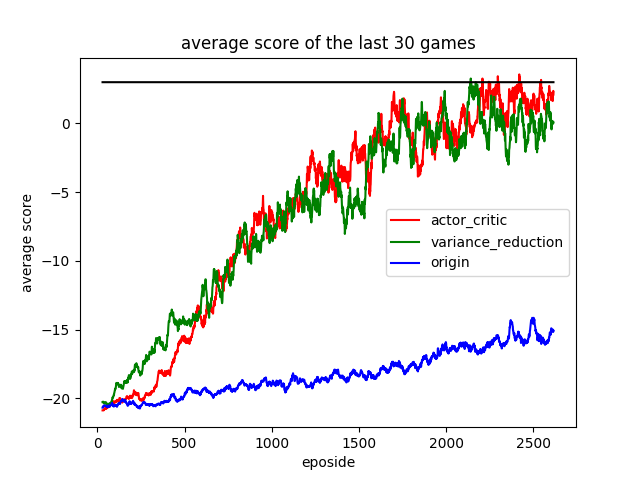
DQN VS DDQN
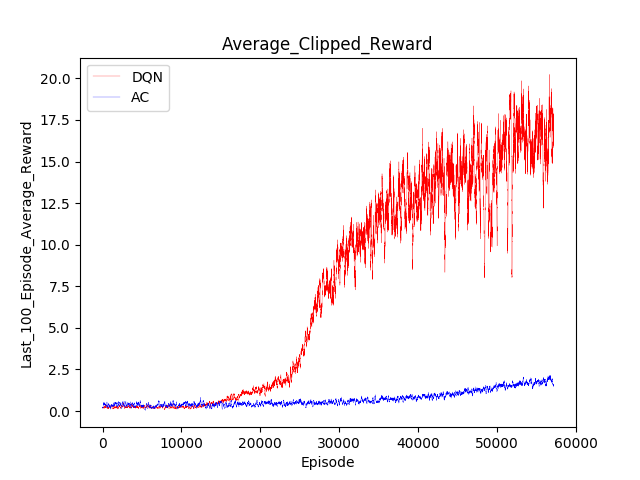
DQN VS Actor critic



Agent at different episode
5000 episode
30000 episode
60000 episode

Title Text
Title Text
DQN Algorithm
1. Play a episode with fixed model and get the reward
- for each state, get (state, action, state', reward)
- store in reply buffer
2. sample
3. Compute y = r + 0.99 * max(Q(s', a')) using target network
4. Compute the gradient between y and Q(s, a) using new network
5. update the new network with gradient
6. repeat to 1.
DDQN Algorithm
1. Play a episode with fixed model and get the reward
- for each state, get (state, action, state', reward)
- store in reply buffer
2. sample
3. Compute y = r + 0.99 * max(Q'(s', argmax(Q(s', a')))) using current network to output the action
4. Compute the gradient between y and Q(s, a) using new network
5. update the new network with gradient
6. repeat to 1.