Intro_autodiff

An introduction to automatic differentiation

[Baydin et al., 2015, Automatic differentiation in machine learning: a survey]

Automatic differentiation ?

- Method to compute the differential of a function using a computer

Input

def f(x):
  return x ** 2


f(1.)
>>>> 1.

Output

g = grad(f)


g(1.)
>>>> 2.0

Automatic differentiation ?

- Method to compute the differential of a function using a computer

Input

def f(x):
  return np.log(1 + x ** 2) / x


f(1.)
>>>> 0.6931471805599453

Output

g = grad(f)


g(1.)
>>>> 0.3068528194400547

Prototypical case

$f$ defined recursively:

$f_0(x) = x$
$f_{k+1}(x) = 4 f_{k}(x) (1 - f_k(x))$

Input

def f(x, n=4):
  v = x
  for i in range(n):
    v = 4 * v * (1 - v)
  return v


f(0.25)
>>>> 0.75

Output

g = grad(f)


g(0.25)
>>>> -16.0

Automatic differentiation is not...

Numerical differentiation

$$f'(x) \simeq \frac{f(x + h) - f(x)}{h}$$

In higher dimension:

$$ \frac{\partial f} {\partial x_i} (\mathbf{x}) \simeq \frac{f(\mathbf{x} + h \mathbf{e}_i) - f(\mathbf{x})}{h}$$

Drawbacks:

Computing $\nabla f = [\frac{\partial f}{\partial x_1}, \cdots, \frac{\partial f}{\partial x_n}]$ takes $n$ computations
Inexact method
How to choose $h$?

Automatic differentiation is not...

Numerical differentiation

Example:

from scipy.optimize import approx_fprime


approx_fprime(0.25, f, 1e-7)
>>>> -16.00001599

Automatic differentiation is not...

Symbolic differentiation

- Takes as input a function specified as symbolic operations

- Apply the usual rules of differentiation to give the derivative as symbolic operations

Example:

$f_4(x) = 64x(1−x)(1−2x)^2 (1−8x+ 8x^2 )^2$, so:

f'_4(x) = 128x(1 − x)(−8 + 16x)(1 − 2x)^2(1 − 8x+ 8x^2)+ 64(1−x)(1−2x)^2(1−8x+ 8x^2)^2−64x(1 − 2x)^2(1 − 8x+ 8x^2)^2 − 256x(1 − x)(1 −2x)(1 − 8x + 8x^2 )^2

Then, evaluate $f'(x)$

Automatic differentiation is not...

Symbolic differentiation

- Exact

- Expression swell: derivatives can have many more terms than the base function

$f_n$ $f'_n$ $f'_n$ (simplified)

Automatic differentiation:

Apply symbolic differentiation at the elementary operation level and keep intermediate numerical results, in lockstep with the evaluation of the main function.

- Function = graph of elementary operations

- Follow the graph and differentiate each operation using differentiation rules (linearity, chain rule, ...)

def f(x, n=4):
  v = x
  for i in range(n):
    v = 4 * v * (1 - v)
  return v


f(0.25)
>>>> 0.75

def g(x, n=4):
  v, dv = x, 1.
  for i in range(n):
    v, dv = 4 * v * (1 - v), 4 * dv * (1 - v) - 4 * v * dv
  return dv


g(0.25)
>>>> -16.0

Forward automatic differentiation:

Apply symbolic differentiation at the elementary operation level and keep intermediate numerical results, in lockstep with the evaluation of the main function.

- Function = graph of elementary operations

- Follow the graph and differentiate each operation using differentiation rules (linearity, chain rule, ...)

- If $f:\mathbb{R}\to \mathbb{R}^m$: need one pass to compute all derivatives :)

- If $f:\mathbb{R}^n \to \mathbb{R}$: need $n$ passes to compute all derivatives :(

- Bad for ML

Reverse automatic differentiation: Backprop

- Function = graph of elementary operations

- Compute the graph and its elements

- Go through the graph backwards to compute the derivatives

def f(x, n=4):
  v = x
  for i in range(n):
    v = 4 * v * (1 - v)
  return v


f(0.25)
>>>> 0.75

def g(x, n=4):
  v = x
  memory = []
  for i in range(n):
    memory.append(v)
    v = 4 * v * (1 - v)
  dv = 1
  for v in memory[::-1]:
    dv = 4 * dv * (1 - v) - 4 * dv * v
  return dv


g(0.25)
>>>> -16.0

Reverse automatic differentiation: Backprop

- Function = graph of elementary operations

- Compute the graph and its elements

- Go through the graph backwards to compute the derivatives

-Only one passe to compute gradients of functions $\mathbb{R}^n \to \mathbb{R}$ :)

Example on a 2d function

$$f(x, y) = yx^2, \enspace x = y= 1$$

Function

$x =1$

$y = 1$

$v_1 = x^2 = 1$

$v_2 =yv_1 = 1$

$f = v_2 =1$

Forward AD (w.r.t. $x$)

Backprop 

$\frac{dx}{dx} =1$

$\frac{dy}{dx} = 0$

$\frac{dv_1}{dx} =2x \frac{dx}{dx} = 2$

$\frac{dv_2}{dx} =y\frac{dv_1}{dx} +v_1 \frac{dy}{dx} =2$

$\frac{df}{dx} = \frac{dv_2}{dx}=2$

$\frac{df}{dv_2}= 1$

$\frac{df}{dy} = \frac{df}{dv_2 }\frac{dv_2}{dy} = \frac{df}{dv_2 }v_1 = 1$

$\frac{df}{dv_1} =y\frac{df}{ dv_2} = 1$

$\frac{df}{dx} = 2 x \frac{df}{dv_1} = 2$

Automatic differentiation:

- Exact

- Takes about the same time to compute the gradient and the function

- Requires memory: need to store intermediate variables

- Easy to use

- Available in Pytorch, Tensorflow, jax, package autograd with numpy

from autograd import grad

g = grad(f)


g(0.25)
>>>> -16.0

Automatic differentiation applications

Example 0: Differentiating a sequence of transforms

Let $g_0, \dots, g_{N-1}$ a sequence of functions, and consider the transform staring from $x$:

- $x_0 = x$

- $x_{n + 1} = g_n(x_n)$ for n=0...N-1

Consider a final cost function $G(x) = \ell(x_N)$ where $\ell$ is differentiable.

What is the gradient of G?

Example 0: Differentiating a sequence of transforms

We can apply forward differentiation (classical chain rule):

$x_{n+1} = g_n(x_n)$ so $\frac{\partial x_{n+1}}{\partial x} = J_n \times \frac{\partial x_n}{\partial x}$.

Iterating this relationship:

$\frac{\partial x_{N}}{\partial x} =J_{N-1}\times \dots\times J_0 $

and finally $\nabla G(x) = \nabla \ell(x_N)J_{N-1}\times \dots\times J_0 $

$J_n$ is the Jacobian of $g_n$ at $x_n$

Example 0: Differentiating a sequence of transforms

- $x_0 = x$

- $x_{n+1} = g_n(x_n)$

- $G(x) = \ell(x_N)$

We have found $\nabla G(x) = \nabla \ell(x_N)J_{N-1}\times \dots\times J_0 $

Will backprop give us another formula?

What is the difference?

Example 1: Computing Stochastic gradients in Neural networks

Neural network with parameters $\theta$: function $f_{\theta}(x)$

E.g. defined recursively:

- $x_0 = x$

- $x_{k + 1} = \sigma(W_kx_k + b_k)$

- $f_{\theta}(x) = x_K$

Here, $\theta = (W_0, b_0, \dots, W_{K - 1}, b_{K-1})$.

Note! Can have much more complicated architecture

Example 1: Computing Stochastic gradients in Neural networks

- $x_0 = x$

- $x_{k + 1} = \sigma(W_kx_k + b_k)$

- $f_{\theta}(x) = x_K$

Supervised learning: we want $f_{\theta}(x) \simeq y$

We have a Training set: $(x^1, y^1), \dots, (x^n, y^n)$

Training program: find $\theta$ that minimizes

$$C(\theta) = \frac1n\sum_{i=1}^n \ell(f_{\theta}(x^i), y^i)$$

Example 1: Computing Stochastic gradients in Neural networks

- $x_0 = x$

- $x_{k + 1} = \sigma(W_kx_k + b_k)$

- $f_{\theta}(x) = x_K$

Minimize

$$C(\theta) = \frac1n\sum_{i=1}^n \ell(f_{\theta}(x^i), y^i)$$

How can we compute $\nabla C(\theta)$?

Autodiff ! $C(\theta)$ is obtained by a sequence of elementary operations.

Example 1: Computing Stochastic gradients in Neural networks

- $x_0 = x$

- $x_{k + 1} = \sigma(W_kx_k + b_k)$

- $f_{\theta}(x) = x_K$

Autodiff is used everywhere in modern machine learning.

Memory issues! To apply bacward autodiff, need to store all intermediate activations $x_k$: sometimes very costly.

Much more expensive to train than to simply evaluate a neural network

Example 2: Learning to learn

Ridge regression: minimize $\ell(\beta) = \frac12 \| X \beta - y\|^2 + \frac\lambda 2\|\beta\|^2$

Gradient descent with step $\rho > 0$ for $T$ iterations:

- $\beta_0 = 0$

- $\beta_{t+1} = \beta_t - \rho( X^{\top}(X\beta -y) + \lambda \beta)$

We see it as a function $GD:\rho \to \beta_T$.

What is the best $\rho$ ?

[Gregor, Lecun, 2010, Learning Fast Approximations of Sparse Coding]

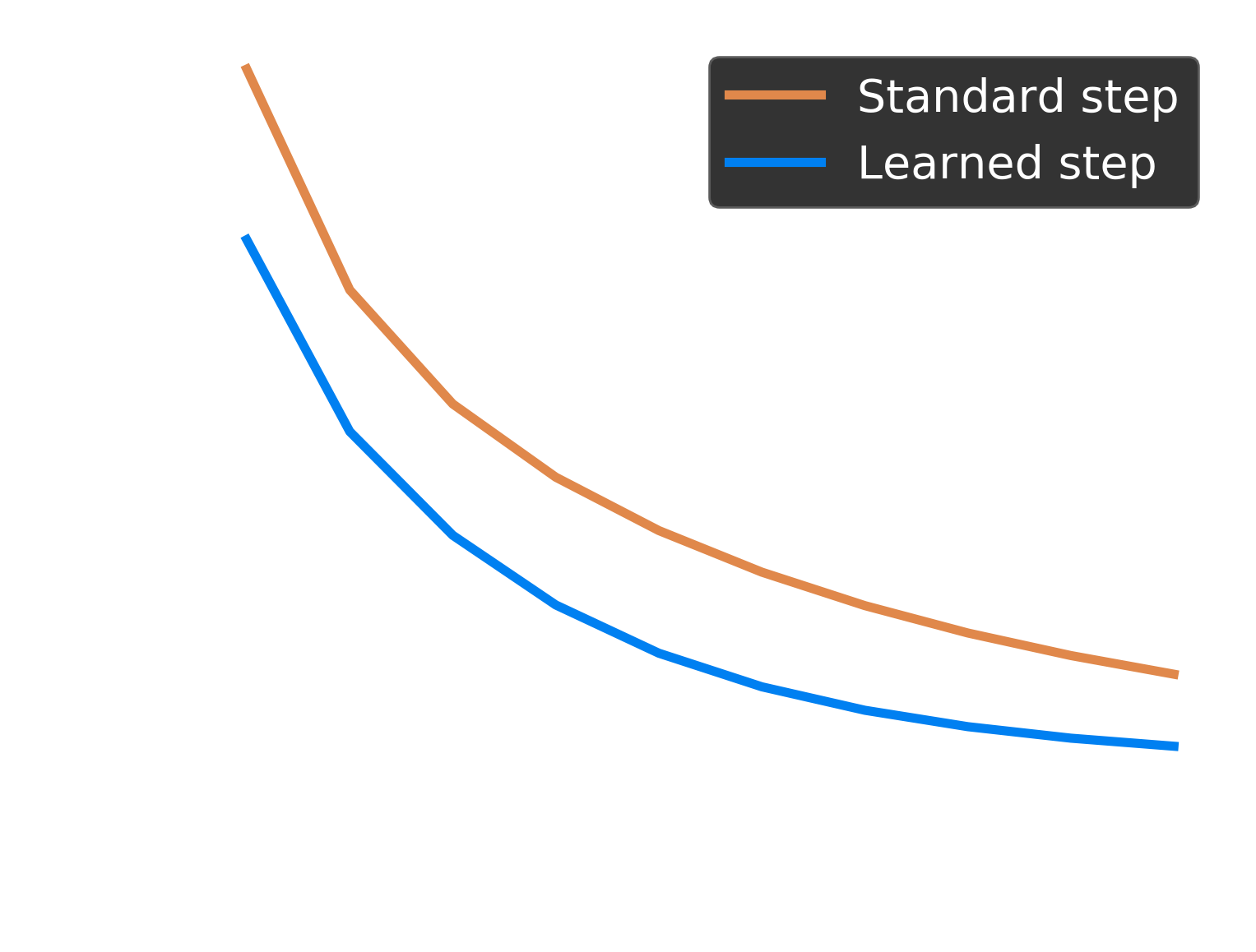
Example 2: Learning to learn

Ridge regression: minimize $\ell(\beta) = \frac12 \| X \beta - y\|^2 + \frac\lambda 2\|\beta\|^2$

We want to find $\rho$ that minimizes $\ell(GD(\rho))$

$\to$ use gradient descent!

$$ \rho \leftarrow \rho - 0.01 \nabla_{\rho}\ell(GD(\rho))$$

$\nabla_{\rho}\ell(GD(\rho))$ is computed using automatic differentiation

Example 3: hyperparameter optimization

Ridge regression: minimize $\ell(\beta, \lambda) = \frac12 \| X \beta - y\|^2 + \frac\lambda 2\|\beta\|^2$

- Assume we have a test set $X_{test}, y_{test}$. Find $\lambda$ that minimizes test error:

$$\ell'(\lambda) = \frac12\|X_{test}\beta^*(\lambda) - y_{test}\|^2$$

subject to :

$$ \beta^*(\lambda) = \arg\min \ell(\beta, \lambda)$$

- In this simple case, closed-form solution for $\beta$, but not in general

[Bengio, 1990, Gradient based optimization of hyperparameters]

Example 3: hyperparameter optimization

Ridge regression: minimize $\ell(\beta, \lambda) = \frac12 \| X \beta - y\|^2 + \frac\lambda 2\|\beta\|^2$

$$\ell'(\lambda) = \frac12\|X_{test}\beta^*(\lambda) - y_{test}\|^2$$

subject to :

$$ \beta^*(\lambda) = \arg\min \ell(\beta, \lambda)$$

Usual approach: grid search. Select a set of candidates $\lambda_1, \dots, \lambda_k$ and pick the one that leads to smallest test error.

Problem: In order to cover space, $k$ grows exponentially with the number of hyperparameters

Grid search is practically useless when more than 10 hyperparameters !

Example 3: hyperparameter optimization

Ridge regression: minimize $\ell(\beta, \lambda) = \frac12 \| X \beta - y\|^2 + \frac\lambda 2\|\beta\|^2$

$$\ell'(\lambda) = \frac12\|X_{test}\beta^*(\lambda) - y_{test}\|^2$$

subject to :

$$ \beta^*(\lambda) = \arg\min \ell(\beta, \lambda)$$

Idea: Use first order information

Example 3: hyperparameter optimization

Ridge regression: minimize $\ell(\beta, \lambda) = \frac12 \| X \beta - y\|^2 + \frac\lambda 2\|\beta\|^2$

$$ \min \ell'(\beta) = \frac12\|X_{test}\beta - y_{test}\|^2 \enspace \text{s.t.} \enspace \beta = \arg\min \ell(\beta, \lambda)$$

- Define the output of gradient descent $GD: \lambda \to \beta$:

$$GD(\lambda) \simeq \argmin_{\beta} \ell(\beta, \lambda)$$

- Optimize $\ell'(GD(\lambda))$ with gradient descent, using autodiff to compute the gradient

Better scaling with # of hyperparameters than grid-search

An introduction to automatic differentiation

Automatic differentiation ?

Automatic differentiation ?

Prototypical case

Automatic differentiation is not...

Automatic differentiation is not...

Automatic differentiation is not...

Automatic differentiation is not...

Automatic differentiation:

Forward automatic differentiation:

Reverse automatic differentiation: Backprop

Reverse automatic differentiation: Backprop

Example on a 2d function

Automatic differentiation:

Automatic differentiation applications

Example 0: Differentiating a sequence of transforms

Example 0: Differentiating a sequence of transforms

Example 0: Differentiating a sequence of transforms

Example 1: Computing Stochastic gradients in Neural networks

Example 1: Computing Stochastic gradients in Neural networks

Example 1: Computing Stochastic gradients in Neural networks

Example 1: Computing Stochastic gradients in Neural networks

Example 2: Learning to learn

Example 2: Learning to learn

Example 3: hyperparameter optimization

Example 3: hyperparameter optimization

Example 3: hyperparameter optimization

Example 3: hyperparameter optimization

Thanks for you attention !