Super-efficiency of automatic differentiation for functions defined as a minimum

https://arxiv.org/abs/2002.03722

Pierre Ablin

Joint work with Gabriel Peyré and Thomas Moreau

ICML 2020

10/05/2021

Optimization topic group

Introduction to automatic differentiation

[Baydin et al., 2015, Automatic differentiation in machine learning: a survey]

https://arxiv.org/abs/1502.05767

Automatic differentiation ?

- Method to compute the differential of a function using  a computer 

Input

def f(x):
  return x ** 2


f(1.)
>>>> 1.

Output

g = grad(f)


g(1.)
>>>> 2.0

Automatic differentiation ?

- Method to compute the differential of a function using  a computer 

Input

def f(x):
  return np.log(1 + x ** 2) / x


f(1.)
>>>> 0.6931471805599453

Output

g = grad(f)


g(1.)
>>>> 0.3068528194400547

Prototypical case 

\(f\) defined recursively:

  • \(f_0(x) = x\)
  • \(f_{k+1}(x)  = 4 f_{k}(x) (1 - f_k(x))\)

Input

def f(x, n=4):
  v = x
  for i in range(n):
    v = 4 * v * (1 - v)
  return v


f(0.25)
>>>> 0.75

Output

g = grad(f)


g(0.25)
>>>> -16.0

Automatic differentiation is not...

Numerical differentiation 

$$f'(x) \simeq \frac{f(x + h) - f(x)}{h}$$

In higher dimension:

$$ \frac{\partial f} {\partial x_i} (\mathbf{x}) \simeq \frac{f(\mathbf{x} + h \mathbf{e}_i) - f(\mathbf{x})}{h}$$

Drawbacks:

  • Computing \(\nabla f = [\frac{\partial f}{\partial x_1}, \cdots, \frac{\partial f}{\partial x_n}]\) takes \(n\) computations 
  • Inexact method
  • How to choose \(h\)?

Automatic differentiation is not...

Numerical differentiation 

Example:  

from scipy.optimize import approx_fprime


approx_fprime(0.25, f, 1e-7)
>>>> -16.00001599

Automatic differentiation is not...

Symbolic differentiation

- Takes as input a function specified as symbolic operations

- Apply the usual rules of differentiation to give the derivative as symbolic operations

 

Example:

\(f_4(x) = 64x(1−x)(1−2x)^2 (1−8x+ 8x^2 )^2\), so:

f'_4(x) = 128x(1 − x)(−8 + 16x)(1 − 2x)^2(1 − 8x+ 8x^2)+ 64(1−x)(1−2x)^2(1−8x+ 8x^2)^2−64x(1 − 2x)^2(1 − 8x+ 8x^2)^2 − 256x(1 − x)(1 −2x)(1 − 8x + 8x^2 )^2

Then, evaluate \(f'(x)\)

Automatic differentiation is not...

Symbolic differentiation

- Exact

- Expression swell: derivatives can have many more terms than the base function

 

        \(f_n\)                                     \(f'_n\)                                          \(f'_n\)  (simplified)

Automatic differentiation:

Apply symbolic differentiation at the elementary operation level and keep intermediate numerical results, in lockstep with the evaluation of the main function.

 

- Function = graph of elementary operations

- Follow the graph and differentiate each operation using differentiation rules (linearity, chain rule, ...)

def f(x, n=4):
  v = x
  for i in range(n):
    v = 4 * v * (1 - v)
  return v


f(0.25)
>>>> 0.75
def g(x, n=4):
  v, dv = x, 1.
  for i in range(n):
    v, dv = 4 * v * (1 - v), 4 * dv * (1 - v) - 4 * v * dv
  return dv


g(0.25)
>>>> -16.0

Forward automatic differentiation:

Apply symbolic differentiation at the elementary operation level and keep intermediate numerical results, in lockstep with the evaluation of the main function.

 

- Function = graph of elementary operations

- Follow the graph and differentiate each operation using differentiation rules (linearity, chain rule, ...)

 

- If \(f:\mathbb{R}\to \mathbb{R}^m\): need one pass to compute all derivatives :)

- If \(f:\mathbb{R}^n \to \mathbb{R}\): need \(n\) passes to compute all derivatives :( 

- Bad for ML

Reverse automatic differentiation: Backprop

- Function = graph of elementary operations

- Compute the graph and its elements

- Go through the graph backwards to compute the derivatives

def f(x, n=4):
  v = x
  for i in range(n):
    v = 4 * v * (1 - v)
  return v


f(0.25)
>>>> 0.75
def g(x, n=4):
  v = x
  memory = []
  for i in range(n):
    memory.append(v)
    v = 4 * v * (1 - v)
  dv = 1
  for v in memory[::-1]:
    dv = 4 * dv * (1 - v) - 4 * dv * v
  return dv


g(0.25)
>>>> -16.0

Reverse automatic differentiation: Backprop

- Function = graph of elementary operations

- Compute the graph and its elements

- Go through the graph backwards to compute the derivatives

 

-Only one passe to compute gradients of functions \(\mathbb{R}^n \to \mathbb{R}\) :)

Example on a 2d function

$$f(x, y) = yx^2, \enspace x = y= 1$$

Function

 \(x =1\) 

 \(y = 1\)

 

 \(v_1 = x^2 = 1\)

 \(v_2 =yv_1 = 1\)

 

\(f = v_2 =1\)

Forward AD (w.r.t. \(x\))

 

 

 

 

 

 

 

 

Backprop \( \)

 

 

 

 

 

 

 

 

 \(\frac{dx}{dx} =1\) 

 \(\frac{dy}{dx} = 0\)

 \(\frac{dv_1}{dx} =2x \frac{dx}{dx} = 2\)

 \(\frac{dv_2}{dx} =y\frac{dv_1}{dx} +v_1 \frac{dy}{dx} =2\)

\(\frac{df}{dx} = \frac{dv_2}{dx}=2\)

 \(\frac{df}{dv_2}= 1\)

 \(\frac{df}{dy} = \frac{df}{dv_2 }\frac{dv_2}{dy} = \frac{df}{dv_2 }v_1 = 1\)

 \(\frac{df}{dv_1} =y\frac{df}{ dv_2} = 1\)

 \(\frac{df}{dx} = 2 x \frac{df}{dv_1} = 2\)

Automatic differentiation:

- Exact

- Takes about the same time to compute the gradient and the function

- Requires memory: need to store intermediate variables 

- Easy to use

- Available in Pytorch, Tensorflow, jax, package autograd with numpy

from autograd import grad

g = grad(f)


g(0.25)
>>>> -16.0

Questions ?

Automatic differentiation for optimization

Example 1: Learning to learn

Ridge regression: minimize \(\ell(\beta) = \frac12 \| X \beta - y\|^2 + \frac\lambda 2\|\beta\|^2\)

 

Gradient descent with step \(\rho > 0\) for \(T\) iterations: 

- \(\beta_0 = 0\)

- \(\beta_{t+1} = \beta_t - \rho( X^{\top}(X\beta -y) + \lambda \beta)\)  

 

We see it as a function \(GD:\rho \to \beta_T\).

 

What is the best \(\rho\) ?

[Gregor, Lecun, 2010, Learning Fast Approximations of Sparse Coding]

Example 1: Learning to learn

Ridge regression: minimize \(\ell(\beta) = \frac12 \| X \beta - y\|^2 + \frac\lambda 2\|\beta\|^2\)

We want to find \(\rho\) that minimizes \(\ell(GD(\rho))\)

 

\(\to\) use gradient descent! 

 

$$ \rho \leftarrow \rho - 0.01 \nabla_{\rho}\ell(GD(\rho))$$

\(\nabla_{\rho}\ell(GD(\rho))\) is computed using automatic differentiation

Example 2: hyperparameter optimization

Ridge regression: minimize \(\ell(\beta, \lambda) = \frac12 \| X \beta - y\|^2 + \frac\lambda 2\|\beta\|^2\)

 

- Assume we have a test set \(X_{test}, y_{test}\).  Minimize test error:

 

$$\ell'(\beta) = \frac12\|X_{test}\beta - y_{test}\|^2$$

subject to :

$$ \beta = \arg\min \ell(\beta, \lambda)$$

 

- In this simple case, closed-form solution for \(\beta\), but not in general

[Bengio, 1990, Gradient based optimization of hyperparameters]

Example 2: hyperparameter optimization

Ridge regression: minimize \(\ell(\beta, \lambda) = \frac12 \| X \beta - y\|^2 + \frac\lambda 2\|\beta\|^2\)

 

$$ \min \ell'(\beta) = \frac12\|X_{test}\beta - y_{test}\|^2 \enspace \text{s.t.} \enspace \beta = \arg\min \ell(\beta, \lambda)$$

- Define the output of gradient descent \(GD: \lambda \to \beta\):

$$GD(\lambda) \simeq \argmin_{\beta} \ell(\beta, \lambda)$$

- Optimize \(\ell'(GD(\lambda))\) with gradient descent, using autodiff to compute the gradient

 

 

Better scaling with # of hyperparameters than grid-search

Questions ?

Super efficiency of autodiff for functions defined as a minimum

https://arxiv.org/abs/2002.03722

Setting:

\ell(x) = \min_z \mathcal{L}(z, x)

- Minimization not in closed-form : sequence \(z_t(x)\) produced by e.g. gradient descent such that \(\mathcal{L}( z_t(x), x) \to \ell(x)\)

 

- How can we estimate \( \nabla \ell(x)\) using \(z_t(x)\)?

 

- Use \(\nabla \ell(x)\) e.g. to minimize / maximize \(\ell\)

The analytic estimator

\ell(x) = \min_z \mathcal{L}(z, x)

- Assume \(\mathcal{L}\) is differentiable and there is \(z^*(x)\) such that \(\ell(x)=\mathcal{L}(z^*(x), x)\)

 

$$\nabla_x\ell(x) = J^*\underbrace{\nabla_z \mathcal{L}(z^*(x), x)}_{=0 } + \nabla_x \mathcal{L}(z^*(x), x)$$

 

 

\(J^*= \frac{\partial z^*}{\partial x}\) is the Jacobian of \(z^*\)

$$\nabla_x\ell(x) =  \nabla_x \mathcal{L}(z^*(x), x)$$

The analytic estimator

\ell(x) = \mathcal{L}(z^*(x), x)

- Given a sequence \(z_t(x)\) approaching \(z^*(x)\), the analytic estimator is:

$$\nabla_x\ell(x) =  \nabla_x \mathcal{L}(z^*(x), x)$$

g^1_t(x) = \nabla_x \mathcal{L}(z_t(x), x)

If \(\nabla_x \mathcal{L} \) is \(L-\)Lipschitz:

$$ |g^1_t (x) - \nabla_x \ell(x)| \leq L |z_t(x) - z^*(x)|$$

 

\(g^1\) converges at the same speed as \(z_t\)

The autodiff estimator

\ell(x) = \mathcal{L}(z^*(x), x)

- Given a sequence \(z_t(x)\) approaching \(z^*(x)\), the autodiff estimator is:

g^2_t(x) = \frac{\partial}{\partial x}\left[ \mathcal{L}(z_t(x), x)\right]

Derivative with respect to \(z_t(x)\) as well:

$$g^2_t(x) = \nabla_x\mathcal{L}(z_t, x) + J_t\nabla_z\mathcal{L}(z_t, x)$$

\(J_t = \frac{\partial z_t}{\partial x}\) is the Jacobian of \(z_t\) 

 

-\(g^2_t\) can be computed at ~ the same cost as \(z_t\)using autodiff

The autodiff estimator

Look at second order expansions:

$$\nabla_x\mathcal{L}(z_t, x) = \nabla_x \ell(x) + \nabla_{xz}\mathcal{L}(z^*, x)(z_t -z^*) + R_{xz}$$

$$\nabla_z\mathcal{L}(z_t, x) =\nabla_{zz}\mathcal{L}(z^*, x) (z_t - z^*) +   R_{zz}$$

Rests are \(R_{xz}, R_{zz} = O(|z_t - z^*|^2)\).

Jacobian error:

$$R(J) = J \nabla_{zz}\mathcal{L}(z^*, x) + \nabla_{xz}\mathcal{L}(z^*, x)$$

 

$$g^2_t(x) = \nabla_x\mathcal{L}(z_t, x) + J_t\nabla_z\mathcal{L}(z_t, x)$$

 

g^2_t - \nabla_x \ell(x) = R(J_t)(z_t - z^*) + R_{xz} + J_t R_{zz}

The autodiff estimator

g^2_t - \nabla_x \ell(x) = \underbrace{R(J_t)(z_t - z^*)}_{?} + \underbrace{R_{xz} + J_t R_{zz}}_{O(|z_t - z^*|^2)}

Implicit functions theorem: 

$$R(J^*) = J^* \nabla_{zz}\mathcal{L}(z^*, x) + \nabla_{xz}\mathcal{L}(z^*, x) = 0$$

 

So if \(J_t \to J^*\) (more later), \(R(J_t) \to 0\) and:

g^2_t = \nabla_x \ell(x) + o(|z_t - z^*|)

\(g^2\) converges faster than \(z_t\)

The implicit estimator

Recall:

$$\nabla_x\ell(x) = J^*\nabla_z \mathcal{L}(z^*(x), x) + \nabla_x \mathcal{L}(z^*(x), x)$$

 

Implicit function theorem:

$$J^* = - \nabla_{xz}\mathcal{L}(z^*, x) \left[\nabla_{zz}\mathcal{L}(z^*, x)\right]^{-1} = \mathcal{J}(z^*, x)$$

 

 

Implicit estimator:

 

$$g^3_t = \mathcal{J}(z_t, x) \nabla_z \mathcal{L}(z_t, x) + \nabla_x \mathcal{L}(z_t, x)$$

The implicit estimator

$$g^3_t = \mathcal{J}(z_t, x) \nabla_z \mathcal{L}(z_t, x) + \nabla_x \mathcal{L}(z_t, x)$$

 

Just like \(g^2\), we have:

 

 

Hence if \(R(\mathcal{J}(z_t, x)) = O(|z_t - z^*|)\):

 

$$ g^3_t = \nabla_x \ell(x) + O(|z_t - z^*|^2)$$

 

g^3_t - \nabla_x \ell(x) = R(\mathcal{J}(z_t, x))(z_t - z^*) + R_{xz} + R(\mathcal{J}(z_t, x)) R_{zz}

\(g^3\) converges twice as fast as \(z_t\)

So far...

$$g^1 - \nabla_x \ell \simeq \enspace z_t - z^*\enspace$$

$$g^2 - \nabla_x \ell <\enspace z_t - z^*\enspace$$

$$g^3 - \nabla_x \ell \simeq (z_t - z^*)^2$$

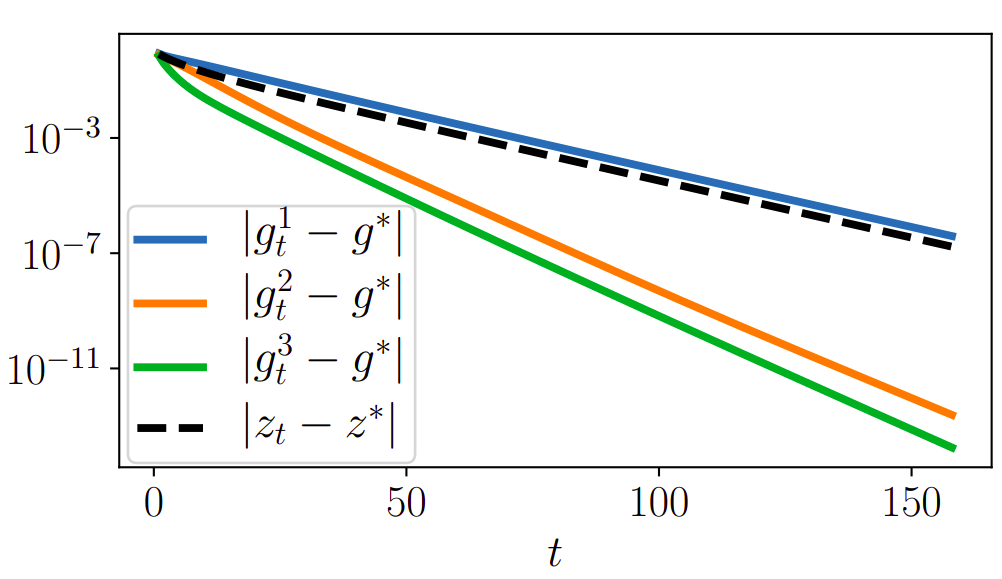
Example on a logistic loss:

$$\mathcal{L}(z, x) = \sum_{i=1}^n \log(1 + \exp(- x_i [Dz]_i)) + \lambda \|z\|^2$$

\(z_t\) obtained with gradient descent:

Tighter analysis of the autodiff estimator

Recall:

$$g^2 - \nabla_x \ell  = R(J_t) (z_t - z^*) + O(|z_t - z^*|^2)$$

We want to analyse \(R(J_t)\).

 

Assume \(z_t(x) \to z^*(x)\), do we have 

$$J_t = \frac{\partial z_t(x)}{\partial x} \to J^* = \frac{\partial z^*(x)}{\partial x}?$$

In general, no :(

$$z_t(x) = \frac1t\sin(tx) \rightarrow 0$$

$$J_t = \cos(tx) \nrightarrow 0$$

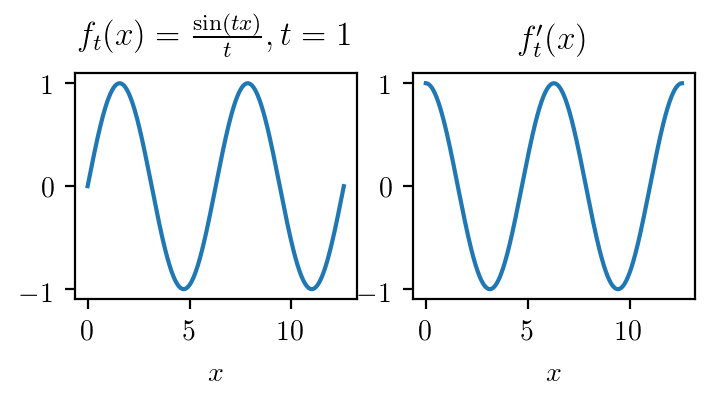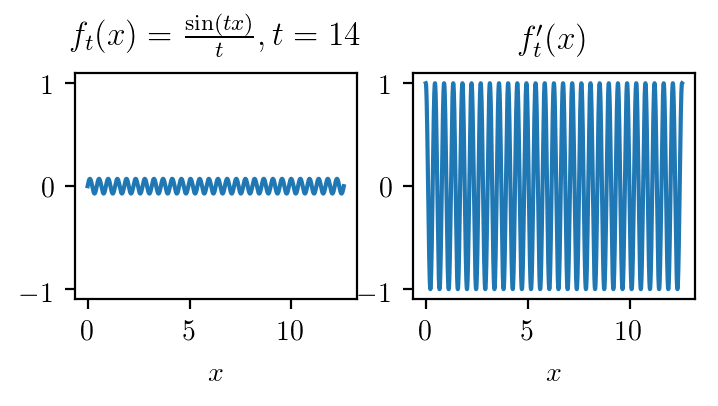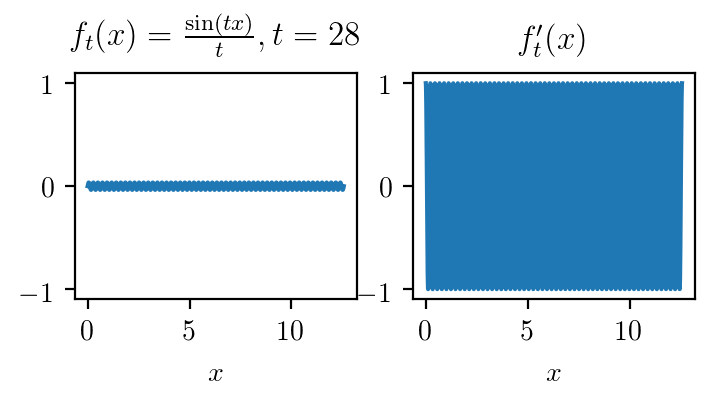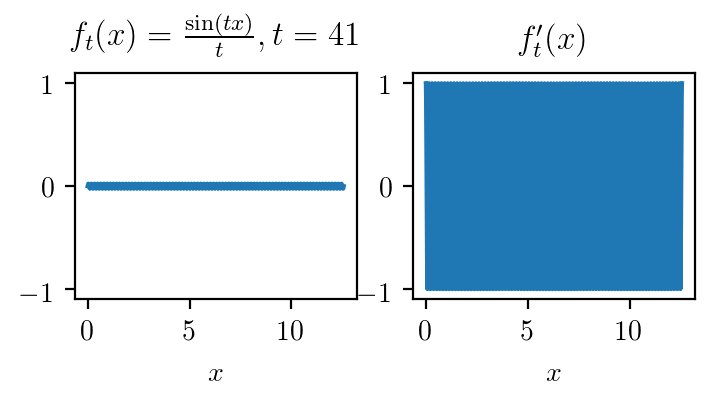
Tighter analysis of the autodiff estimator

Assume \(\mathcal{L}\) is \(\mu\)-strongly convex and \(L\)-smooth w.r.t. \(z\), and that \(z_t\) is obtained by gradient descent:

$$z_{t+1}(x) = z_t(x) - \rho \nabla_z\mathcal{L}(z_t(x), x)$$

Then,

$$|z_t - z^*| = O(\kappa^t)$$

$$\|J_t - J^*\| = O(t \kappa^t), \enspace \kappa = 1 - \rho \mu$$

We obtain \(z^t\) using optimization methods \(\to\) no such problem.

 

Theorem:

 

\(J_t\) converges slightly slower than \(z_t\)

Bounds in the strongly convex setting

Assume \(\mathcal{L}\) is \(\mu\)-strongly convex and \(L\)-smooth w.r.t. \(z\), and that \(z_t\) is obtained by gradient descent:

$$z_{t+1}(x) = z_t(x) - \rho \nabla_z\mathcal{L}(z_t(x), x)$$

Then,

$$g^1 - \nabla_x\ell(x) = \enspace O(\kappa^{t})$$

$$g^2 - \nabla_x\ell(x) = O(t\kappa^{2t})$$

$$g^3 - \nabla_x\ell(x) = \enspace O(\kappa^{2t})$$

Beyond linear convergence

For SGD / a class of non-strongly convex functions (p-Lojasiewicz),  we get:

 

$$g^1 - \nabla_x\ell(x) = O(z_t - z^*)\enspace \enspace$$

$$g^2 - \nabla_x\ell(x) = O((z_t-z^*)^2)$$

$$g^3 - \nabla_x\ell(x) =  O((z_t-z^*)^2)$$

SGD example:

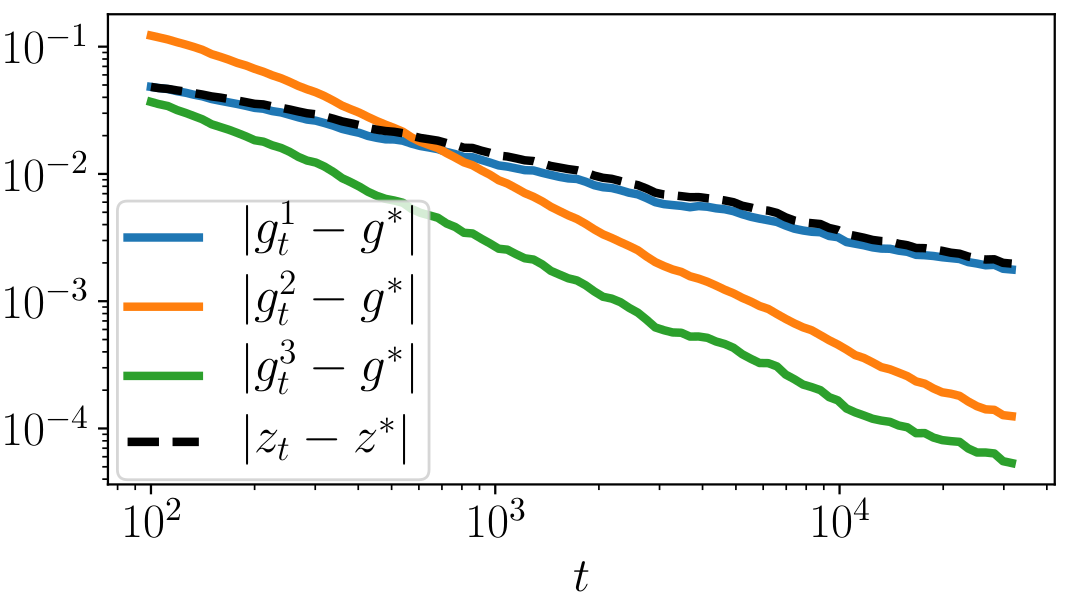
In practice:

In the linear convergence case:

$$g^1 - \nabla_x\ell(x) = \enspace O(\kappa^{t})$$

$$g^2 - \nabla_x\ell(x) = O(t\kappa^{2t})$$

$$g^3 - \nabla_x\ell(x) = \enspace O(\kappa^{2t})$$

But...

 

-Computing \(g^2\) is about twice as costly as \(g^1\) \(\to\) pointless to use \(g^2\)

$$g^2_{t} \simeq g^1_{2t}$$

-Computing \(g^3\) involves matrix inversion / big operators 

In practice:

In the sub-linear convergence case:

$$g^1 - \nabla_x\ell(x) = O(1 / t)\enspace$$

$$g^2 -\nabla_x\ell(x) = O(1 / t^2)$$

$$g^3 - \nabla_x\ell(x) = O(1 / t^2)$$

 

-Much better to use \(g^2\) than \(g^1\)

Thanks for you attention !

Made with Slides.com