Learning with Riemannian manifolds

Pierre Ablin and Florian Yger

Machine learning

Data : $x_1,\dots, x_n$

Algorithm: parametrized map

$$f_{\theta}: x\to y$$

(linear model, neural network,...)

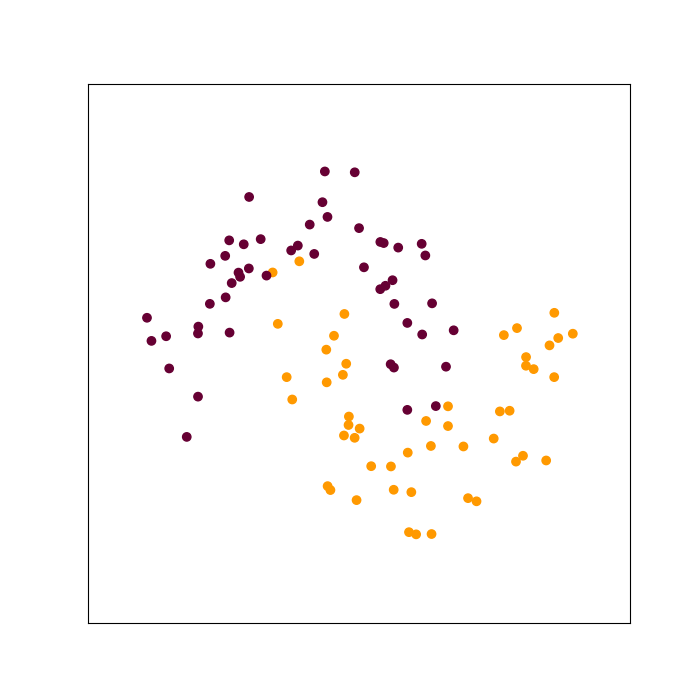
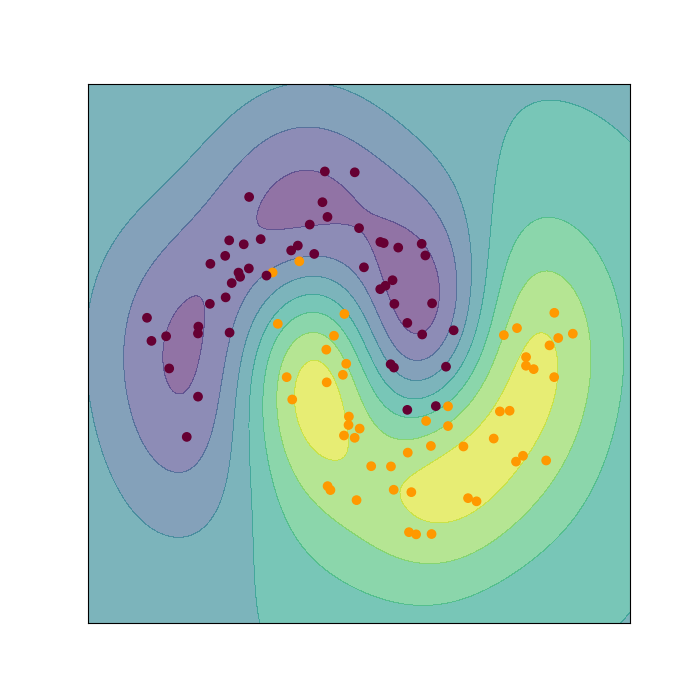
Riemannian manifolds

$\mathcal{M}$ high-dimensional "surface" that locally resembles a vector space.

Endow vector space with a metric.

Examples:

- Sphere $S^{p-1}= \{x\in\mathbb{R}^p| \enspace \|x\|=1\}$

- Orthogonal matrices $$\mathcal{O}_p = \{X\in \mathbb{R}^{p\times p}| \enspace X^\top X = I_p\}$$

- Positive matrices $S^{++}_p$

Well studied mathematical objects

Manifolds in machine learning

ML Algorithm: parametrized map

$$f_{\theta}: \enspace x\to y$$

Parameters $\theta$ on manifold

To impose a prior
For stability
For robustness...

Training algorithms on manifolds

Data $x$ on manifold

Geometric data
Structured data
...

Design algorithms to handle data that lives on manifolds

Training ML models with parameters on a manifold

One motivation: robust neural networks

Trained without care, a neural network is susceptible to adversarial attacks

Given data $x$, a small perturbation $\delta$ such that $\|f_{\theta}(x + \delta) - f_{\theta}(x)\|\gg \|\delta\|$

Goodfellow, Ian J., Jonathon Shlens, and Christian Szegedy. "Explaining and harnessing adversarial examples."

Certified robustness with orthogonal weights

Idea : The map $x\mapsto Wx$ is norm preserving when $W^\top W = I_p$

We can stack such transforms to get networks such that

$$\|f_{\theta}(x + \delta) - f_{\theta}(x)\| \leq \|\delta\|$$

Certified robustness !

Pinot, R., Meunier, L., Araujo, A., Kashima, H., Yger, F., Gouy-Pailler, C., & Atif, J. Theoretical evidence for adversarial robustness through randomization.

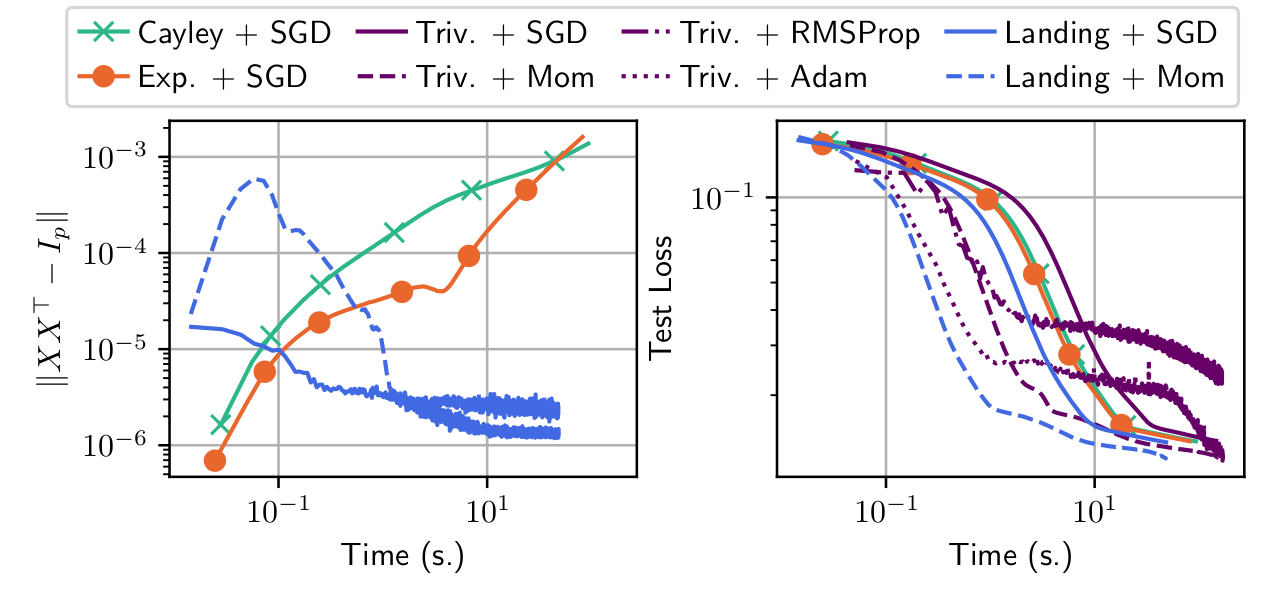
Training a network with orthogonal weights

Training = optimization

Training with orthogonal weights = optimization on a manifold

Well established field but deep learning brings a new context:

Hardware: use of GPU's
Massive data: need to use stochastic algorithms

Contribution:

Fast training of neural nets with orthogonal weights

Ablin, P. and Peyré, G. Fast and accurate optimization on the orthogonal manifold without retraction. AISTATS 2022

Training ML models with data on a manifold

Use-case in BCI

EEG signals are usually :

multidimensional
noisy

Riemannian & Euclidean geometries for 2x2 PSD matrices

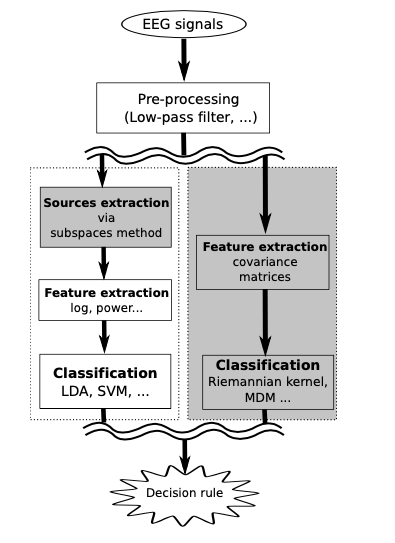
Covariance matrices are now used as EEG features

Yger, F., Berar, M., Lotte, F., Riemannian approaches in Brain-Computer Interfaces: a review

Corsi, MC., Yger, F., Chevallier, S., RIGOLETTO-- A contribution to the Clinical BCI Challenge--WCCI2020

golden standard
simpler pipelines
more robust models

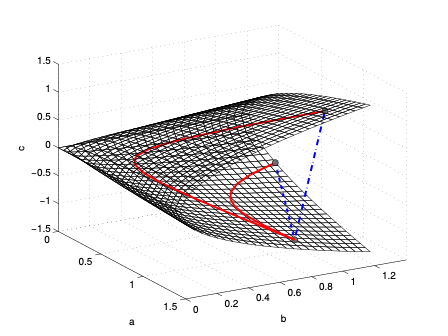
Missing data on manifolds

Averaging on manifold

$$\min_{S \in \mathcal{P}_n } \sum_i \delta_R^2 (\Sigma_i,S)$$

leads to simple (yet efficient) MDM classifiers

Yger, F., Chevallier, S., Barthélemy, Q., Sra. S. Geodesically-convex optimization for averaging partially observed covariance matrices

Averaging on manifold with missing columns

$$\min_{S \in \mathcal{P}_n } \sum_i \delta_R^2 (M_i^\top\Sigma_i M_i,M_i^\top S M_i)$$

But when the signals from some sensors are missing, things are different ...

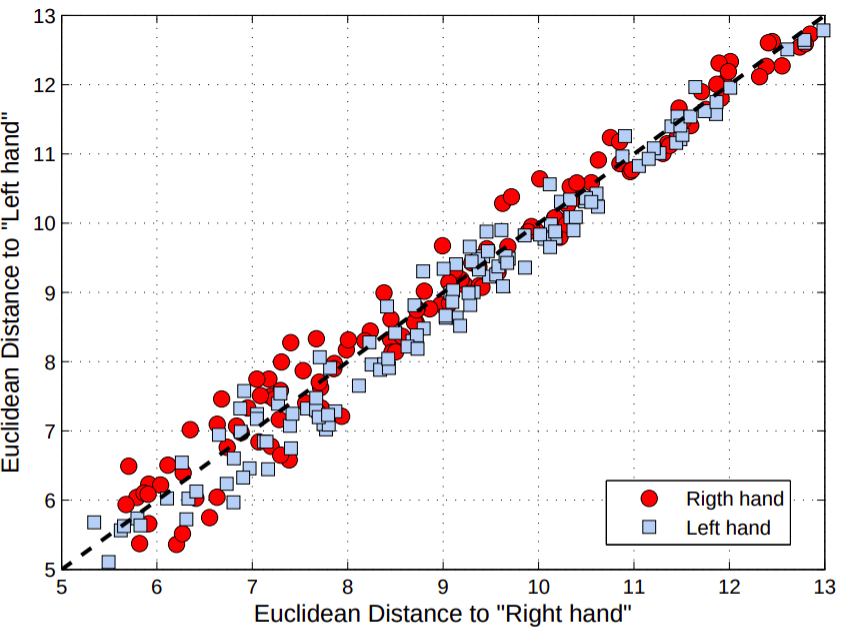
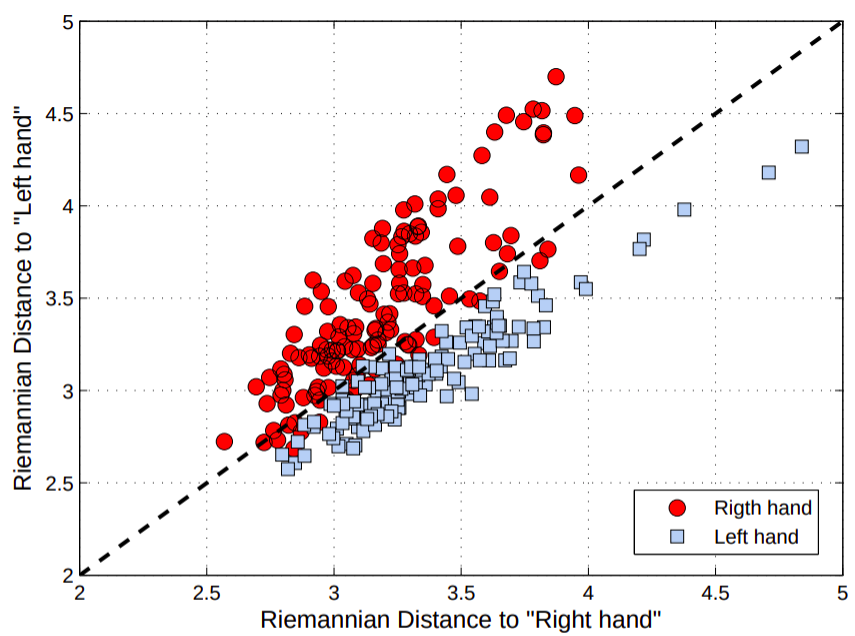
Projects and

Future Works

Manifolds & Deep Learning

Develop deep architectures that are robust using orthogonal layers
Fast training of such networks on modern hardware

Optimal transport meets manifolds

Trajectories to model

frequency information
$$\{\Sigma^{f_m}, \cdots, \Sigma^{f_m} \}$$
non-stationarity
$$\{\Sigma^{t_m}, \cdots, \Sigma^{t_m} \}$$

$$\Sigma^1$$

$$\Sigma^m$$

Part of a WP in a submitted ANR project