FAST AND ACCURATE OPTIMIZATION ON THE ORTHOGONAL MANIFOLD WITHOUT RETRACTION
Pierre Ablin
CNRS - Université paris-dauphine
Reference:
Pierre Ablin and Gabriel Peyré.
Fast and accurate optimization on the orthogonal manifold without retraction. AISTATS 2022
https://arxiv.org/abs/2102.07432
Orthogonal weights in a neural network ?
Orthogonal matrices
A matrix \(W \in\mathbb{R}^{p\times p}\) is orthogonal if
$$W^\top W = I_p$$
applications in Neural networks
- Adversarial robustness
- Stability
- To build invertible networks
Training neural networks with orthogonal weights
Training problem
Neural network \(\phi_{\theta}: x\mapsto y\) with parameters \(\theta\). Dataset \(x_1, \dots, x_n\).
Find parameters by empirical risk minimization:
$$\min_{\theta}f(\theta) = \frac1n\sum_{i=1}^n\ell_i(\phi_{\theta}(x_i))$$
How to do this with orthogonal weights?
Loss function
Orthogonal manifold
\( \mathcal{O}_p = \{W\in\mathbb{R}^{p\times p}|\enspace W^\top W =I_p\}\) is a Riemannian manifold:
Around each point, it looks like a linear vector space.
Problem:
$$\min_{W\in\mathcal{O}_p}f(W)$$
"Classical" approach:
Extend Euclidean algorithms to the Riemannian setting (gradient descent, stochastic gradient descent...)
Absil, P-A., Robert Mahony, and Rodolphe Sepulchre. Optimization algorithms on matrix manifolds.
Tangent space
\(T_W\) : tangent space at \(W\).
Set of all tangent vectors at \(W\).
Simple set for \(\mathcal{O}_p\):
$$T_W = \{Z\in\mathbb{R}^{p\times p}|\enspace ZW^\top + WZ^\top = 0\}$$
$$T_W = \mathrm{Skew}_p W$$
Set of skew-symmetric matrices
Riemannian gradient
Tangent space:
$$T_W = \{Z\in\mathbb{R}^{p\times p}|\enspace ZW^\top + WZ^\top = 0\}$$
$$T_W = \mathrm{Skew}_p W$$
Riemannian gradient:
$$\mathrm{grad}f(W) = \mathrm{proj}_{T_W}(\nabla f(W)) \in T_W$$
On \(\mathcal{O}_p\):
$$\mathrm{grad}f(W) = \mathrm{Skew}(\nabla f(W)W^\top) W$$
Projection on the skew-symmetric matrices: \(\mathrm{skew}(M) = \frac12(M - M^\top)\)
Knowing \(\nabla f(W)\), only need 2 matrix-matrix multiplications to compute it : cheap !
Moving on the manifold
We cannot go in a straight line:
$$W^{t+1} = W^t - \eta \mathrm{grad}f(W^t)$$
Goes out of \(\mathcal{O}_p\) :(
Retractions: examples
On \(\mathcal{O}_p\), \(T_W = \mathrm{Skew}_pW\), hence for \(Z\in T_W\) we can write
$$Z = AW,\enspace A^\top = -A$$
Classical retractions :
- Exponential: \(\mathcal{R}(W, AW) =\exp(A)W\)
- Cayley: \(\mathcal{R}(W, AW) =(I -\frac A2)^{-1}(I + \frac A2)W\)
- Projection: \(\mathcal{R}(W, AW) = \mathrm{Proj}_{\mathcal{O_p}}(W + AW)\)
Riemannian gradient descent
- Start from \(W_0\in\mathcal{O}_p\)
- Iterate \(W^{t+1} = \mathcal{R}(W^t, -\eta\mathrm{grad} f(W^t))\)
Today's problem: retractions are often very costly for deep learning
COmputational cost
Riemannian gradient descent for a neural network:
- Compute \(\nabla f(W)\) using backprop
- Compute \(\mathrm{grad}f(W) = \mathrm{Skew}(\nabla f(W)W^\top)W\)
- Move using a retraction \(W\leftarrow \mathcal{R}(W, -\eta \mathrm{grad} f(W))\)
Classical retractions :
- Exponential: \(\mathcal{R}(W, AW) =\exp(A)W\)
- Cayley: \(\mathcal{R}(W, AW) =(I -\frac A2)^{-1}(I + \frac A2)W\)
- Projection: \(\mathcal{R}(W, AW) = \mathrm{Proj}_{\mathcal{O_p}}(W + AW)\)
These are:
- costly linear algebra operations
- not suited for GPU (hard to parralelize)
- can be the most expensive step
Rest of the talk: find a cheaper alternative
Main idea
In a deep learning setting, moving on the manifold is too costly !
Can we have a method that is free to move outside the manifold that
- Still converges to the solutions of \(\min_{W\in\mathcal{O}_p} f(W)\)
- Has cheap iterations ?
Spoiler: yes !

Projection "paradox''
Take a matrix \(M\in\mathbb{R}^{p\times p}\)
How to check if \(M\in\mathcal{O}_p\) ?
Just compute \(\|MM^\top - I_p\|\) and check if it is close to 0.
But projecting \(M\) on \(\mathcal{O}_p\) is expensive:
$$\mathcal{Proj}_{\mathcal{O}_p}(M) = (MM^\top)^{-\frac12}M$$
Projection "paradox''
Take a matrix \(M\in\mathbb{R}^{p\times p}\)
It is cheap and easy to check if \(M\in\mathcal{O}_p\).
Just compute \(\|MM^\top - I_p\|\) and check if it is close to 0.
Idea: follow the gradient of $$\mathcal{N}(M) = \frac14\|MM^\top - I_p\|^2$$
$$\nabla \mathcal{N}(M) = (MM^\top - I_p)M$$
The iterations \(M^{t+1} = M^t - \eta\nabla \mathcal{N}(M^t)\) converge to the projection
Special structure : symmetric matrix times M...
optimization and projection
Projection
Follow the gradient of $$\mathcal{N}(M) = \frac14\|MM^\top - I_p\|^2$$
$$\nabla \mathcal{N}(M) = (MM^\top - I_p)M$$
$$\mathrm{grad}f(M) = \mathrm{Skew}(\nabla f(M)M^\top) M$$
These two terms are orthogonal !
Optimization
Riemannian gradient:
The landing field
Projection
Follow the gradient of $$\mathcal{N}(M) = \frac14\|MM^\top - I_p\|^2$$
$$\nabla \mathcal{N}(M) = (MM^\top - I_p)M$$
Optimization
Riemannian gradient:
$$\mathrm{grad}f(M) = \mathrm{Skew}(\nabla f(M)M^\top) M$$
$$\Lambda(M) = \mathrm{grad}f(M) + \lambda \nabla \mathcal{N}(M)$$
The landing field
$$\nabla \mathcal{N}(M) = (MM^\top - I_p)M$$
$$\mathrm{grad}f(M) = \mathrm{Skew}(\nabla f(M)M^\top) M$$
$$\Lambda(M) = \mathrm{grad}f(M) + \lambda \nabla \mathcal{N}(M)$$
Because of orthogonality of the two terms:
$$\Lambda(M) = 0$$
if and only if
- \(MM^\top - I_p = 0\) so \(M\) is orthogonal
- \(\mathrm{grad}f(M) = 0\) so \(M\) is a critical point of \(f\) on \(\mathcal{O}_p\)
The landing field is cheap to compute
$$\Lambda(M) = \left(\mathrm{Skew}(\nabla f(M)M^\top) + \lambda (MM^\top-I_p)\right)M$$
Only matrix-matrix mutliplications ! No expensive linear algebra + parrallelizable on GPU's
Comparison to retractions:

The Landing algorithm:
$$\Lambda(M) = \left(\mathrm{Skew}(\nabla f(M)M^\top) + \lambda (MM^\top-I_p)\right)M$$
Starting from \(M^0\in\mathcal{O}_p\), iterate
$$M^{t+1} = M^t -\eta \Lambda(M^t)$$
convergence result
$$\Lambda(M) = \left(\mathrm{Skew}(\nabla f(M)M^\top) + \lambda (MM^\top-I_p)\right)M$$
Starting from \(M^0\in\mathcal{O}_p\), iterate
$$M^{t+1} = M^t -\eta \Lambda(M^t)$$
Theorem (informal):
If the step size \(\eta\) is small enough, then we have for all \(T\):
$$\frac1T\sum_{t=1}^T\|\mathrm{grad} f(M^t)\|^2 = O(\frac1T)$$
$$\frac1T\sum_{t=1}^T\mathcal{N}(M^t) = O(\frac1T)$$
Same rate of convergence as classical Riemannian gradient descent
Convergence to \(\mathcal{O}_p\)
Experiments
Procrustes problem
$$f(W) = \|AW - B\|^2,\enspace A, B\in\mathbb{R}^{p\times p}$$
$$p=40$$
Comparison to other Riemannian methods with retractions
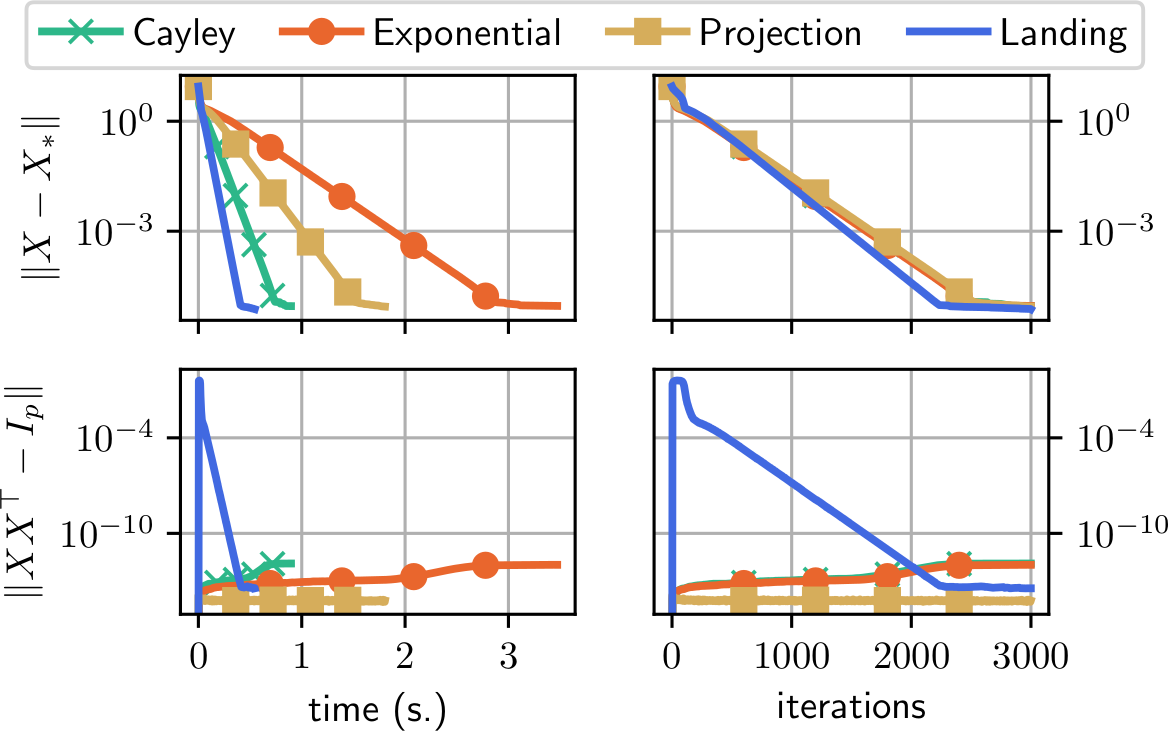
Same convergence curve as classical Riemannian gradient descent
One iteration is cheaper hence faster convergence
Distance to the manifold: increases at first then decrease
Neural networks: Training a resnet on cifar
Model: residual network, with convolutions with orthogonal kernels
Trained on CIFAR-10 (dataset of 60K images, 10 classes)
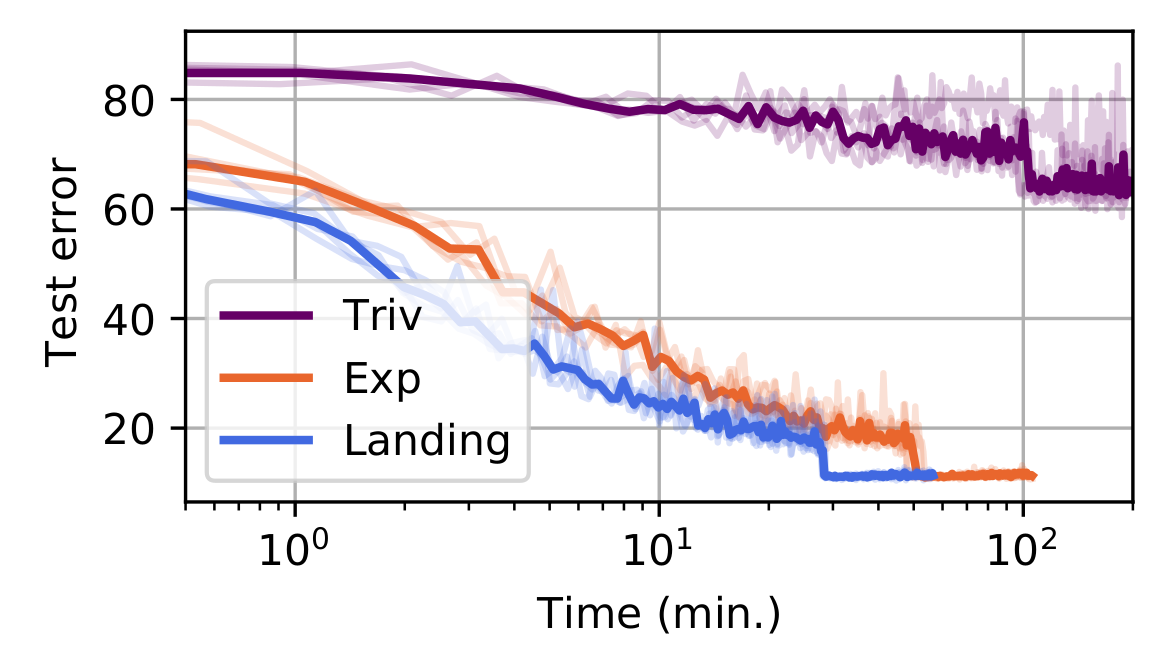
Conclusion
- Landing method: useful when retractions are the bottleneck in optimization algorithms
- Possible extensions to the Stiefel manifold (for rectangular matrices)
- Possible extensions to SGD, variance reduction, etc...
Thanks !
