The LASSO:

least absolute shrinkage and selection operator

 

Pierre Ablin

12/03/2019

Parietal Tutorial

Overview

  • Linear regression
  • The Lasso model
  • Non-smooth optimization: proximal operators

Supervised learning

y \in \mathbb{R}, \enspace \mathbf{x} \in \mathbb{R}^P, \enspace \varepsilon = \mathcal{N}(0, \sigma^2), \enspace f: \mathbb{R}^P \rightarrow \mathbb{R}
y = f(\mathbf{x}) + \varepsilon

GOAL: Learn \( f \) from some realizations of \( (\mathbf{x}, y) \)

Linear regression

y = f(\mathbf{x}) + \varepsilon

GOAL: Learn \( f \) from some realizations of \( (\mathbf{x}, y) \)

Assumption: 

\(f\) is linear

f(\mathbf{x}) = \beta_1x_1 + \beta_2 x_2 + \cdots + \beta_P x_P = \mathbf{x}^{\top} \mathbf{\beta}

GOAL: Learn \( \beta \) from some realizations of \( (\mathbf{x}, y) \)

Maximum likelihood?

y = \mathbf{x}^{\top} \mathbf{\beta} + \varepsilon

For one sample, if we observe \(  \mathbf{x}_{\text{obs}}\) and \( y_{\text{obs}} \) , we have:

p(y = y_{\text{obs}} | \mathbf{x} = \mathbf{x}_{\text{obs}}) = p( \mathbf{x}_{\text{obs}}^{\top} \mathbf{\beta} + \varepsilon = y_{\text{obs}}| \mathbf{x} = \mathbf{x}_{\text{obs}})

i.e. :

 

p(y = y_{\text{obs}} | \mathbf{x} = \mathbf{x}_{\text{obs}}) = p(\varepsilon = y_{\text{obs}} - \mathbf{x}_{\text{obs}}^{\top} \mathbf{\beta}) \\ = \frac{1}{\sqrt{2 \pi \sigma^2}} \exp{(- \frac{( y_{\text{obs}} - \mathbf{x}_{\text{obs}}^{\top} \mathbf{\beta})^2}{2\sigma^2})}

Maximum likelihood?

 

For one sample, if we observe \(  \mathbf{x}_{\text{obs}}\) and \( y_{\text{obs}} \) , we have:

p(y = y_{\text{obs}} | \mathbf{x} = \mathbf{x}_{\text{obs}}) = \frac{1}{\sqrt{2 \pi \sigma^2}} \exp{(- \frac{( y_{\text{obs}} - \mathbf{x}_{\text{obs}}^{\top} \mathbf{\beta})^2}{2\sigma^2})}

If we observe a whole dataset of \(N\) i.i.d. samples$$ (\mathbf{x}_1,y_1), \cdots, (\mathbf{x}_N, y_N) \enspace, $$

the likelihood of this observation is:

\mathcal{L}(\beta) = p(y_1 = y_1, \cdots, y_N = y_N | \mathbf{x}_1 = \mathbf{x}_1, \cdots, \mathbf{x}_N=\mathbf{x}_N) \\ = p(y_1 = y_1| \mathbf{x}_1 = \mathbf{x}_1) \times \cdots \times p(y_N = y_N| \mathbf{x}_N = \mathbf{x}_N) \\

maximum likelihood estimator:

\beta_{\text{MLE}} = \arg\max \mathcal{L}(\beta) = \arg\min \sum_{n=1}^N \frac12 (y_n - \mathbf{x}_n^{\top} \beta)^2

Matrix interlude

Define the \(\ell_2\) norm of a vector:

$$|| \mathbf{v}|| = \sqrt{\sum_{n=1}^N v_n^2}$$

And note in condensed matrix form:

$$ \mathbf{y} = [y_1,\cdots, y_N]^{\top} \in \mathbb{R}^N$$

X = [\mathbf{x}_1,\cdots,\mathbf{x}_N]^{\top}\in\mathbb{R}^{N \times P}

Then, 

\sum_{n=1}^N (y_n - \mathbf{x}_n^{\top} \beta)^2 = ||\mathbf{y} - X \beta||^2

M.L.E.

 

\beta_{\text{MLE}} = \arg\min \frac12 ||\mathbf{y} - X \beta||^2

Pros:

  • Consistant: as \( N \rightarrow \infty \), \(\beta_{\text{MLE}} \rightarrow \beta^* \)
  • Comes from a clear statistical framework
  • Can behave badly when the model is mispecified (e.g. \(f\) is not really linear)
  • Lots of variance in \(\beta_{\text{MLE}}\) when \(N\) is not big enough
  • Ill posed problem when \(N < P\) ! 

Cons:

What do we do when n < p?

Bet on sparsity / Ockham's razor: only a few coefficients in \( \beta \) play a role

The \( \ell_0 \) Norm:

\ell_0(\beta) = \text{Number of non-zero coefficients in }\beta

Example:

(1.1, 2.5, -6.3, 4.1) \rightarrow 4 \\ (1.1, 0, 0, 4.1) \rightarrow 2 \\ (0, 0, 0, 0) \rightarrow 0

Subset selection/matching pursuit

Idea: select only a few active coefficients with the \( \ell_0 \) norm.

\beta_{\text{subset}} = \arg\min \frac12 || \mathbf{y} - X\beta ||^2 \enspace \text{subject to} \enspace \ell_0(\beta) \leq t

Where \( t\) is an integer controlling the sparsity of the solution.

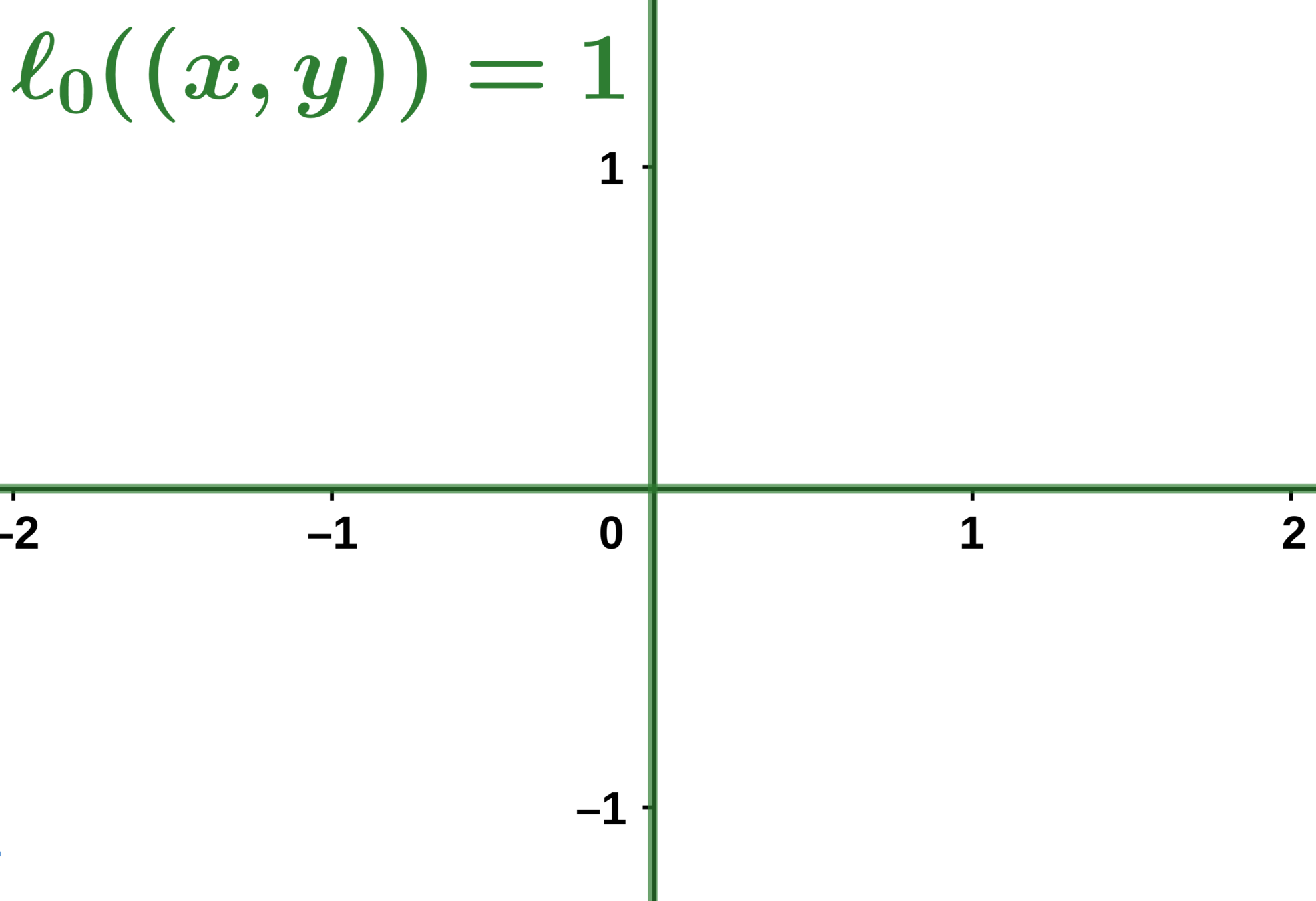
  • Non-convexity
  • Instability: adding a sample may completely change \( \beta \)  and its support.
  • NP-Hard (loooong to solve)

Problems:

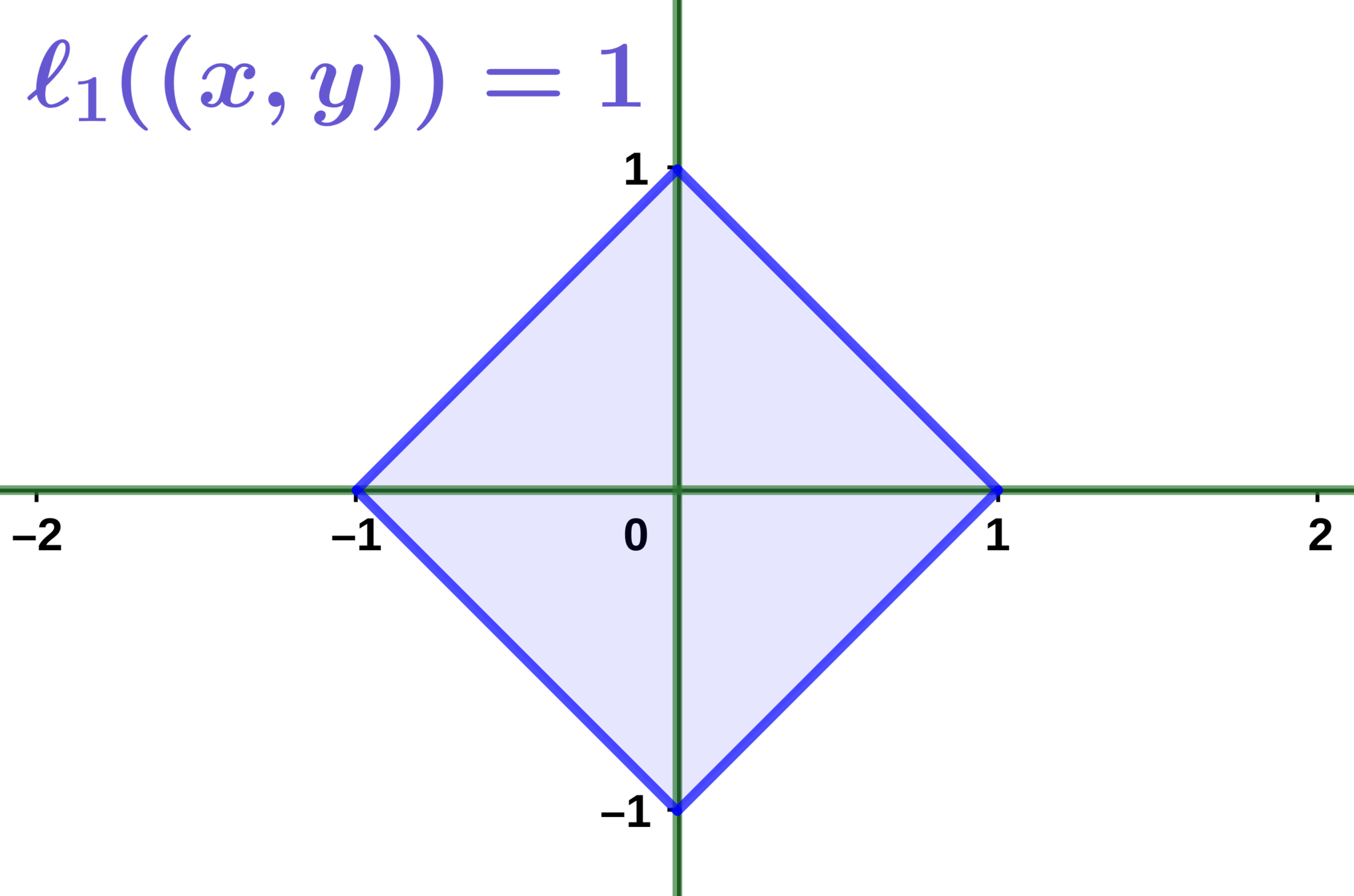
The Lasso

Idea: relax the \(\ell_0\) norm to obtain a convex problem

\beta_{\text{lasso}} = \arg\min \frac12 || \mathbf{y} - X\beta ||^2 \enspace \text{subject to} \enspace \ell_1(\beta) \leq t

Where \( t\) is a level controlling the sparsity of the solution.

 

See notebook

 

\ell_1(\beta) = |\beta |_1 = |\beta_1| + \cdots + |\beta_P|

The Lasso: Lagrange formulation

\beta_{\text{lasso}} = \arg\min \frac12 || \mathbf{y} - X\beta ||^2 + \lambda |\beta|_1

Where \( \lambda \) is a level controlling the amount of sparsity.

  • Relationship between \(\lambda\) and \(t\) depends on the data
  • It promotes sparsity: there is a threshold \(\lambda_{\text{max}}\) such that  \( \lambda >\) \(\lambda_{\text{max}}\)  implies \(\beta_{\text{lasso}} = 0 \)

Derivation

\(\beta = 0\) is a solution to the lasso if:

0 \in \partial_{\beta=0}(\frac12 ||y - X \beta||^2 + \lambda |\beta|_1)

Where \(\partial \) is the subgradient.

\partial(\frac12 || y - X\beta||^2) = \{X^{\top}X\beta - X^{\top} y\}
\partial_{\beta=0}(\lambda|\beta|_1) = [-\lambda, \lambda]^P

So the condition writes:

\forall p, \enspace (X^{\top}y)_p \in [-\lambda , \lambda]
\lambda_{\text{max}} = |X^{\top}y|_{\infty}

Lasso is useful because...

  • It performs at the same time model selection and estimation : it tells you which coefficients in \(\mathbf{x}\) are important.

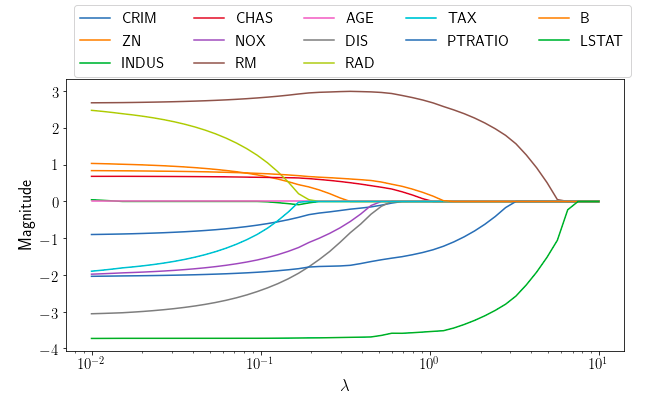
Boston dataset:

Lasso is useful because...

  • Leveraging sparsity enables fast solvers

If \(p = 1000 \) and \(n = 1000 \), computing \(X\beta\) takes \(\sim n \times p = 10^6 \) operations

Intuition:

But if we know that there are only \(10 \) non-zero coefficients in \(\beta\), it takes only \(\sim 10^4\) operations

The same reasoning applies to most quantities useful to estimate the model

Lasso estimation

how do we fit the model?

Gradient descent 101

Minimize \( f(\mathbf{x})\) where \(f\) is differentiable.

Iterate \(\mathbf{x}^{t+1} = \mathbf{x}^t - \eta \nabla f(\mathbf{x}^t) \)

Equivalent to minimizing a quadratic surrogate:

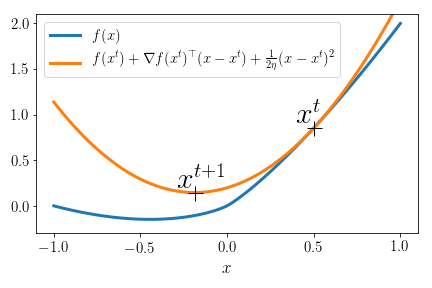
\mathbf{x}^{t+1} = \arg\min_{\mathbf{x}} f(\mathbf{x}^t) + \nabla f(\mathbf{x}^t)^{\top}(\mathbf{x} - \mathbf{x}^t) + \frac{1}{2\eta} ||\mathbf{x} - \mathbf{x}^t||_2^2

The simplest lasso:

\(P=1, N = 1, X = 1:\) can we minimize \(\frac12 (y - \beta)^2 + \lambda |\beta|\) ?

Yes: proximity operator

\text{prox}_{|\cdot |}(y, \lambda) = \arg\min_{\beta} \frac12(y-\beta)^2 + \lambda |\beta|

Soft-thresholding:

\text{prox}_{|\cdot |}(y, \lambda) =
  • \(0\) if \(|y|\leq \lambda\)
  • \(y- \lambda\) if \(y>\lambda\)
  • \(y + \lambda\) if \(y < -\lambda\) 

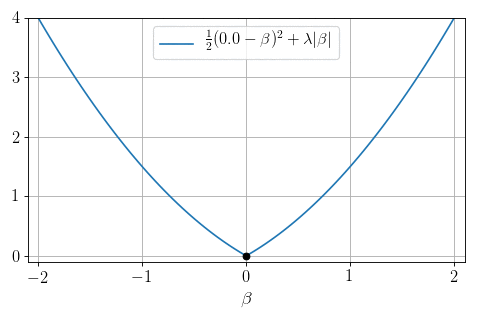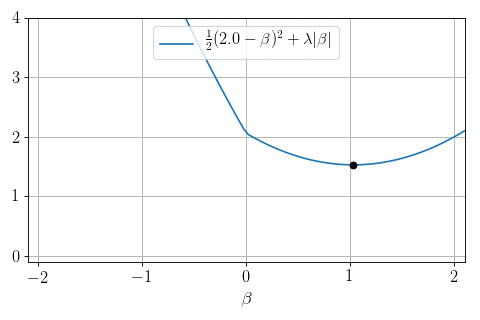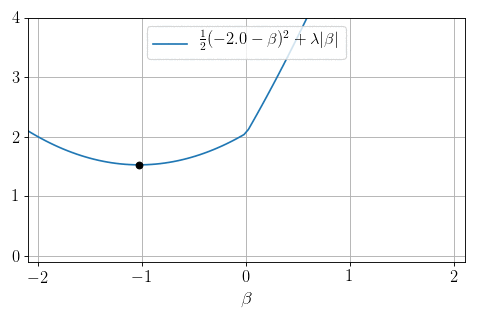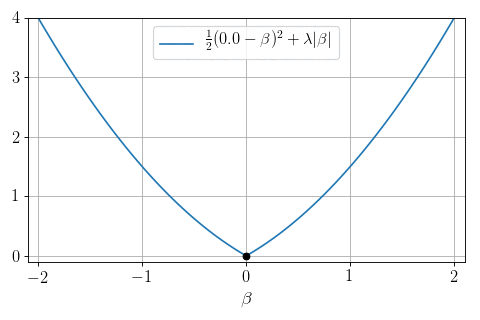
Soft thresholding

\text{st}(y, \lambda) =
  • \(0\) if \(|y|\leq \lambda\)
  • \(y- \lambda\) if \(y>\lambda\)
  • \(y + \lambda\) if \(y < -\lambda\) 

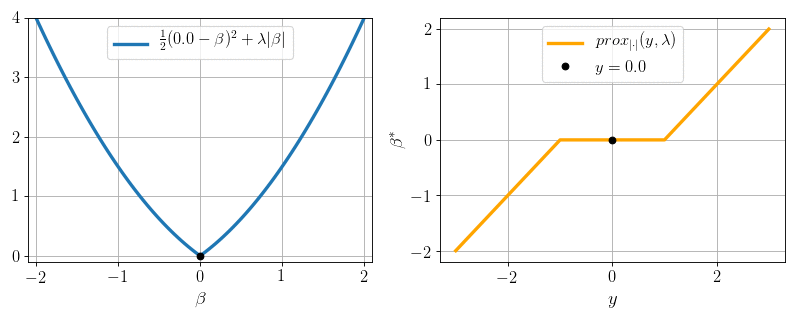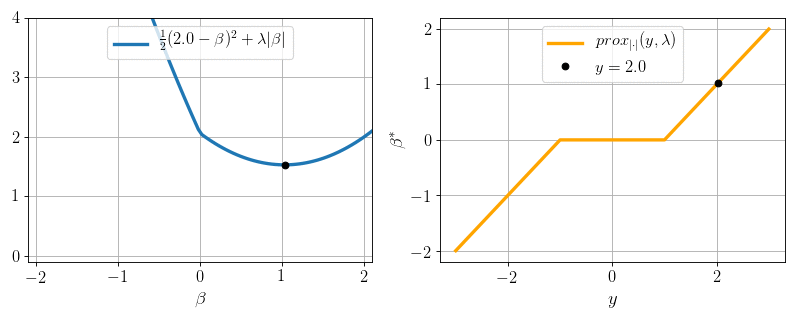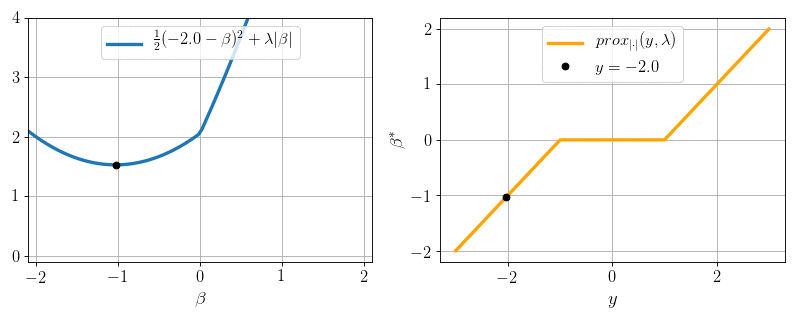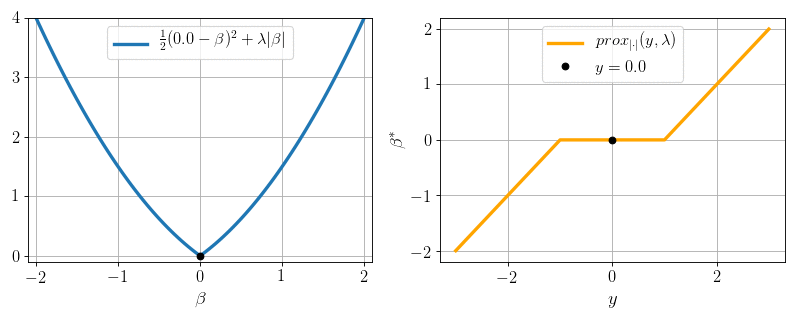
Separability:

\text{prox}_{|\cdot |_1}(\mathbf{z}, \lambda) = \arg\min_{\beta}\frac12 ||\mathbf{z} - \beta ||^2 + \lambda |\beta|_1 =(\text{st}(z_1, \lambda), \cdots, \text{st}(z_P, \lambda))

ISTA: Iterative soft threshdolding algorithm

\beta_{\text{lasso}} = \arg\min \frac12 || \mathbf{y} - X\beta ||^2 + \lambda |\beta|_1

Gradient of the smooth term: 

\nabla_{\beta}(\frac12||\mathbf{y} - X \beta ||^2) = X^{\top}( X \beta - \mathbf{y})
\beta^{t+1} = \text{prox}_{|\cdot|_1}(\beta^{t} - \eta X^{\top}(X\beta^{t} - \mathbf{y}), \lambda\eta)

ISTA:

Comes from:

\mathbf{\beta}^{t+1} = \arg\min_{\beta} f(\mathbf{\beta}^t) + \nabla f(\beta^t)^{\top}(\beta - \beta^t) + \frac{1}{2\eta} ||\beta - \beta^t||_2^2 + \lambda |\beta|_1

ISTA: Iterative soft threshdolding algorithm

\beta^{t+1} = \text{prox}_{|\cdot|_1}(\beta^{t} - \eta X^{\top}(X\beta^{t} - \mathbf{y}), \lambda\eta)
  • Some coefficients are \(0\) because of the prox
  • One iteration takes \(O(\min(N, P) \times P)\)

Can be problematic for large \(P\) !

COORDInate descent

\beta^{t+1}_j = \text{prox}_{|\cdot|_1}(\beta^{t}_j - \eta X[j, :]^{\top}(X\beta^{t} - \mathbf{y}), \lambda\eta)

Idea : update only one coefficient of \( \beta \) at each iteration.

  • If we know the residual \( \mathbf{r} =X\beta^{t} - \mathbf{y}\), each update is \(O(n) \) :)

Residual update: 

After updating the coordinate \(j\):

\mathbf{r} \leftarrow \mathbf{r} + (\beta^{\text{new}}_j - \beta^{\text{old}}_j)X[j, :]

\( \beta^{t+1}_i = \beta^{t}_i \)  for \( i \enspace \ne j \)

Thanks!

Made with Slides.com