Discrete Autoencoders
Gumbel-Softmax
vs
Improved Semantic Hashing
Piotr Kozakowski
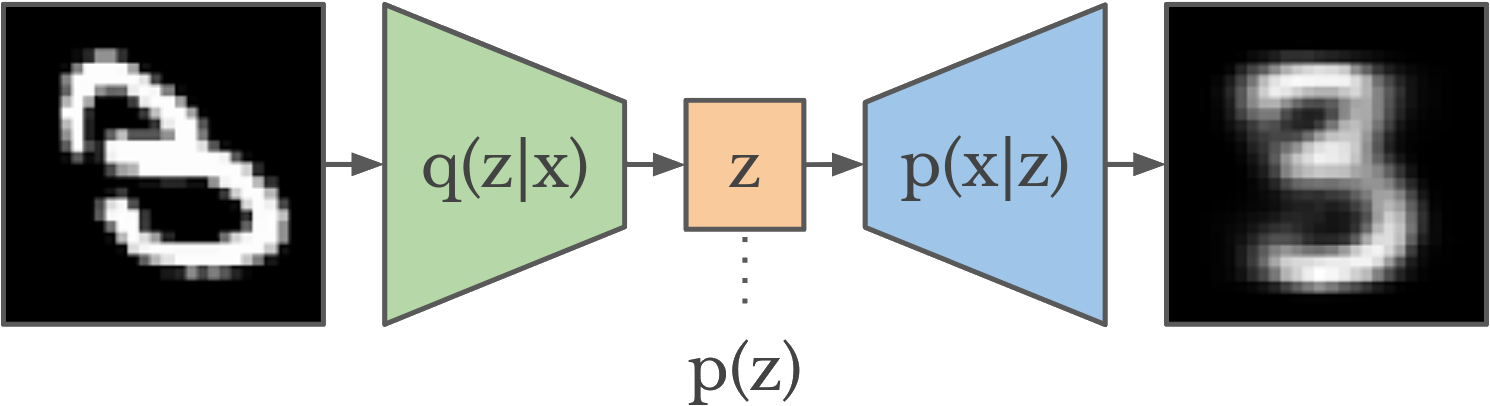
Variational Autoencoders
maximize
Variational Autoencoders
maximize
Training procedure:
- sample
- sample
- compute loss:
- backpropagate and update
Variational Autoencoders
Training procedure:
- sample
- sample
- compute loss:
- backpropagate and update
Commonly,
and
How to backpropagate through
?
Reparametrization trick
Commonly,
and
How to backpropagate through
?
Let
and
.
Backpropagate as usual, treating
as a constant.
Why Discrete?
- exactness
- better fit for some problems
- data compression
- easy lookup
Why Discrete in RL?
- learning combinatoric structures (e.g. approximate MDP - VaST)
- better fit for some problems (e.g. modeling stochasticity of the environment - SimPLe)
Corneil et al. - Efficient Model-Based Deep Reinforcement Learning with Variational State Tabulation (2018)
Kaiser et al. - Model-Based Reinforcement Learning for Atari (2019)
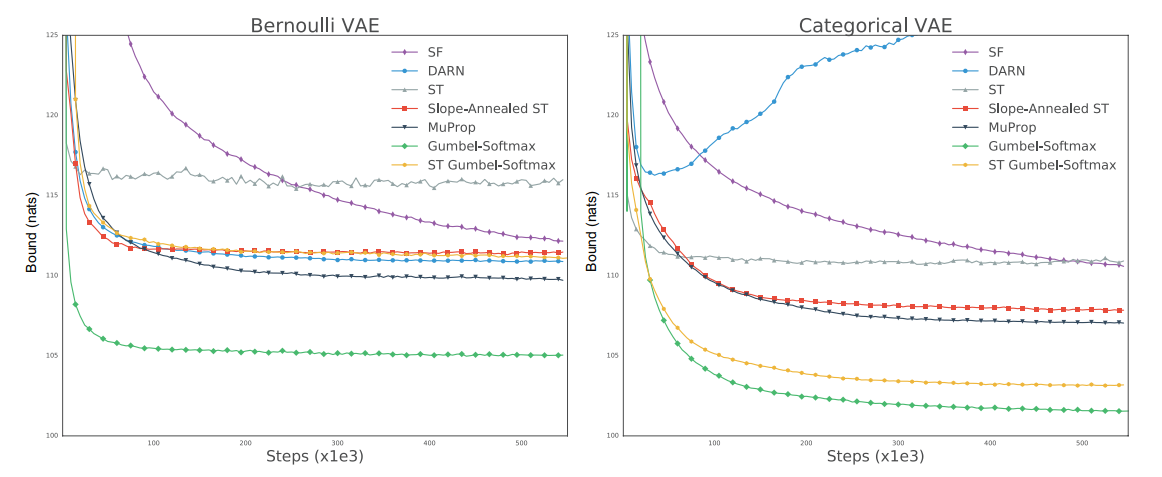
Gumbel-Softmax
Reparametrization trick for the categorical distribution:
Still can't backpropagate though.
generates a sample
with
with
generates a sample
Jang et al - Categorical Reparameterization with Gumbel-Softmax, 2016
Gumbel-Softmax
Approximate
with
with
Temperature annealing: as
,
is differentiable - can backpropagate!
Jang et al - Categorical Reparameterization with Gumbel-Softmax, 2016
Gumbel-Softmax
Drop-in replacement for the normal distribution in VAE:

Gumbel-Softmax
def sample_gumbel(shape, eps=1e-20):
u = torch.rand(shape)
return -torch.log(-torch.log(u + eps) + eps)
def gumbel_softmax(logits, temperature):
y = logits + sample_gumbel(logits.size())
return F.softmax(y / temperature, dim=-1)Gumbel-Softmax
Improved Semantic Hashing
Discretize
half of the time,
but backpropagate as if it was not discretized.
Binary latent variables.
with
Noise forces
to extreme values.
Kaiser et al - Discrete Autoencoders for Sequence Models, 2018
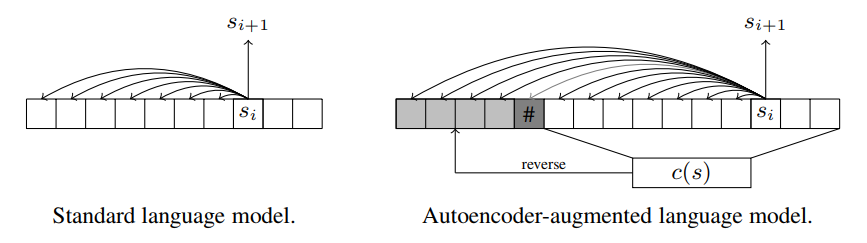
Improved Semantic Hashing
No probabilistic interpretation and no KL loss.
No prior to sample the latent from.
Solution: predict the latent autoregressively as a sequence of bits using an LSTM.
Predict several bits at a time.
Source: Tensor2Tensor
Improved Semantic Hashing
def saturating_sigmoid(logits):
return torch.clamp(
1.2 * torch.sigmoid(logits) - 0.1, min=0, max=1
)
def mix(a, b, prob=0.5):
mask = (torch.rand_like(a) < prob).float()
return mask * a + (1 - mask) * b
def improved_semantic_hashing(logits, noise_std=1):
noise = torch.normal(
mean=torch.zeros_like(logits), std=noise_std
)
noisy_logits = logits + noise
continuous = saturating_sigmoid(noisy_logits)
discrete = (
(noisy_logits > 0).float() +
continuous - continuous.detach()
)
return mix(continuous, discrete)Improved Semantic Hashing
Improved Semantic Hashing
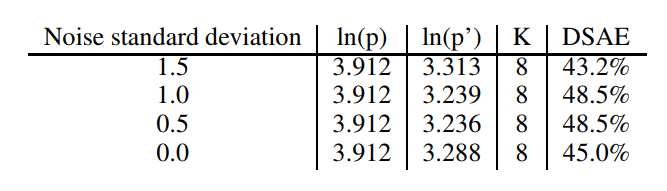
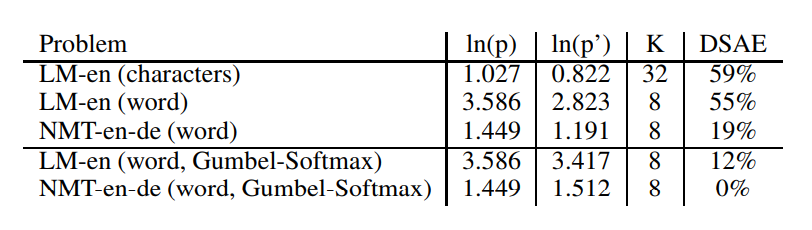
Theoretical comparison
Gumbel-softmax
- temperature annealing
- annealing rate needs tuning
- any categorical variables
- sampling from the prior
Improved semantic hashing
- stationary Gaussian noise
- robust to hyperparameters
- just binary variables
- no explicit way to sample
MNIST image reconstruction
Procedure:
- sample an image from MNIST
- encode
- discretize without noise
- decode
Metric: binary cross-entropy
MNIST image generation
Procedure:
- sample a discrete latent code
- decode
Metric: Inception score
for a generator
and pretrained classifier
Reconstruction
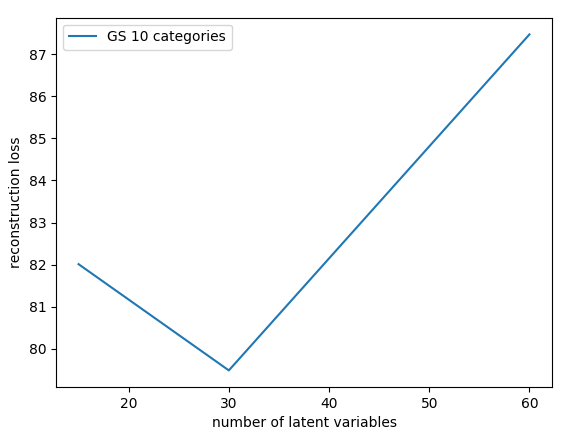
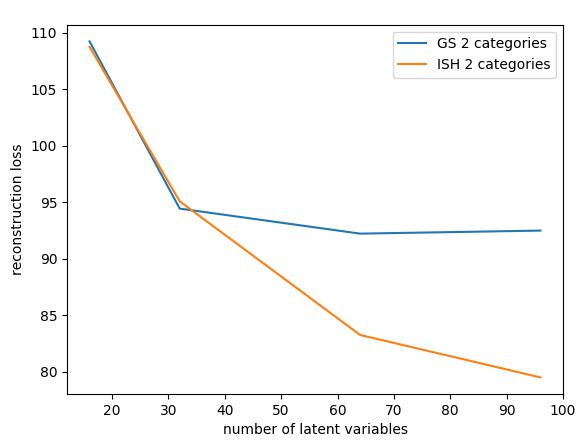
Reconstruction
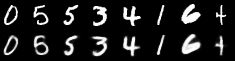
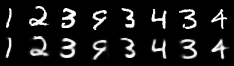
GS, 30 x 10
ISH, 96 x 2
Sampling
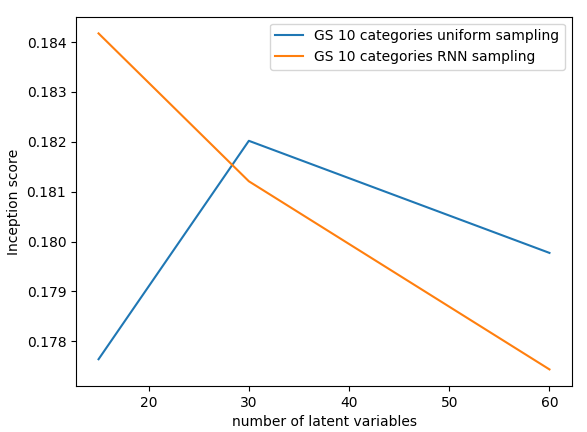
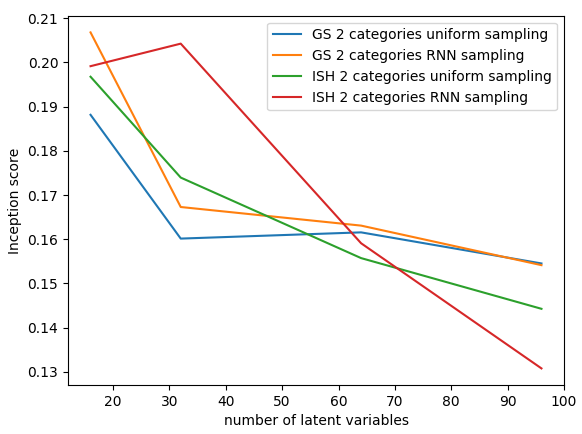
Sampling

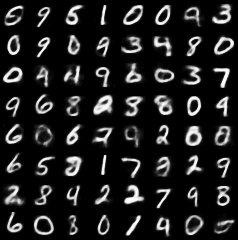
GS, 16 x 2
ISH, 32 x 2
Conclusions
- methods achieve comparable results
- GS is better at sampling
- ISH reconstruction scales much better with the number of variables
- GS is sensitive to the number of categories
- ISH has less hyperparameters to tune
- in both methods sampling is better with binary variables and RNN
Speaker:
Presentation:
Code:
References:
Jang et al. - Categorical Reparameterization with Gumbel-Softmax (2016)
Kaiser et al. - Discrete Autoencoders for Sequence Models (2018)
Corneil et al. - Efficient Model-Based Deep Reinforcement Learning with Variational State Tabulation (2018)
Kaiser et al. - Model-Based Reinforcement Learning for Atari (2019)
https://slides.com/piotrkozakowski/discrete-autoencoders
https://github.com/koz4k/gumbel-softmax-vs-discrete-ae
Piotr Kozakowski