Fast Differentiable Sorting and Ranking
ICML 2020
presented by Piotr Kozakowski
Sorting and ranking are important.
Sorting and ranking are important.
But not differentiable.
Sorting and ranking are important.
But not differentiable.
Sorting: piecewise linear - continuous, derivatives constant, zero or undefined.
Sorting and ranking are important.
But not differentiable.
Sorting: piecewise linear - continuous, derivatives constant, zero or undefined.
Ranking: piecewise constant - discontinuous, derivatives zero or undefined.
Goal: construct differentiable approximations of sorting and ranking.
Definitions
Example
Discrete optimization formulations
Permutahedron
Convex hull of permutations on w.
Permutahedron in 3d
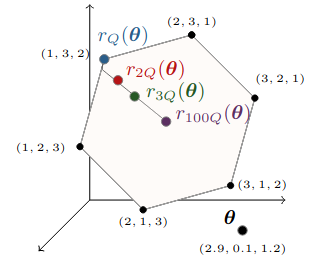
source: the paper
Permutahedron in 4d
source: Wikipedia
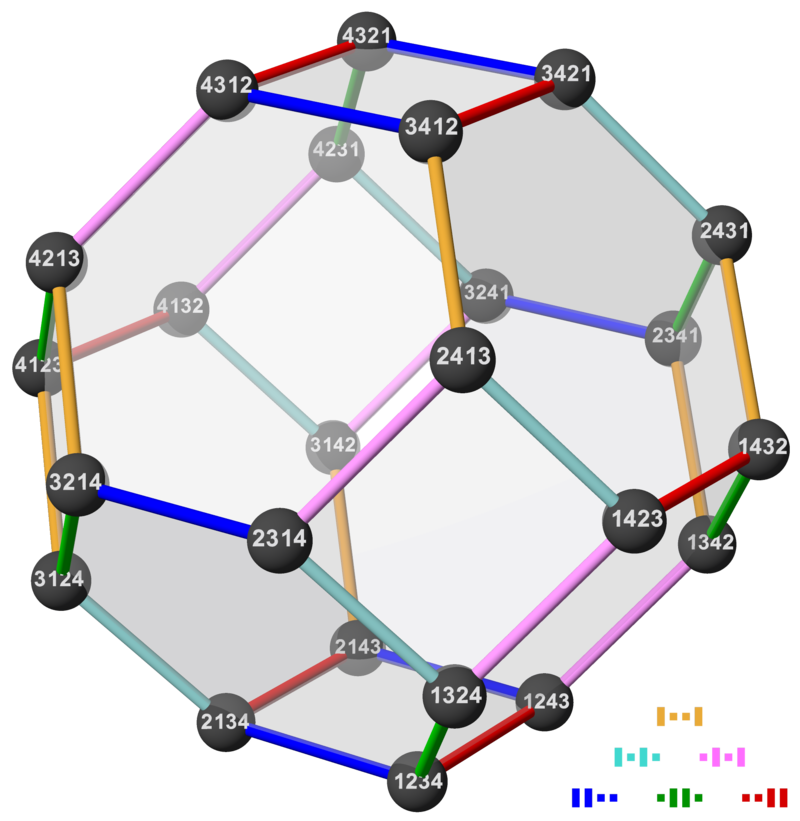
Linear programming formulations
Linear programming formulations
same solutions
from the Fundamental Theorem of Linear Programming
Generalization
Regularization
Regularization
Regularization
Euclidean projection of z onto the permutahedron!
Regularization
Regularization
(not going to talk about that)
How does it work?

Properties

Effect of regularization strength
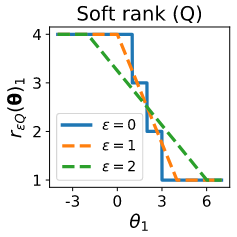
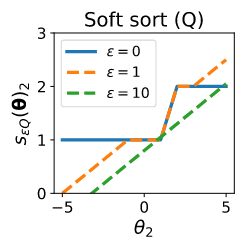
Reduction to isotonic regression
TLDR: we can pose the problem as isotonic regression
and solve it in O(n log n) time and O(n) space.
And we can multiply with the Jacobian in O(n).
(it's sparse)
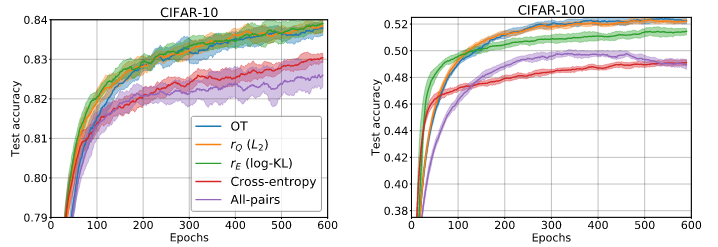
Experiment: top-1 classification on CIFAR
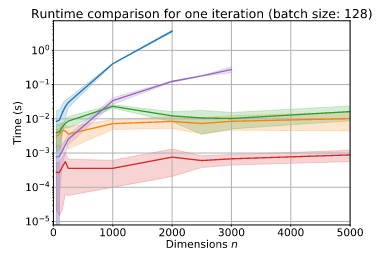
Experiment: robust regression
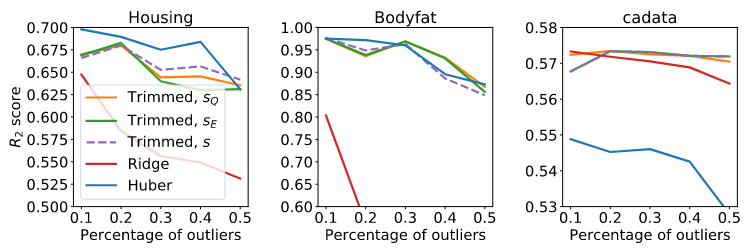
Idea: sort the losses and ignore the top k of them.