Using Transformers to teach Transformers how to train Transformers
Piotr Kozakowski
joint work with Łukasz Kaiser and Afroz Mohiuddin
at Google Brain

Hyperparameter tuning
Hyperparameters in deep learning:
- learning rate
- dropout rate
- moment decay in adaptive optimizers
- ...
Tuning is important, but hard.
Done manually, takes a lot of time.
Needs to be re-done for every new architecture and task.
Hyperparameter tuning
Some require scheduling, which takes even more work.
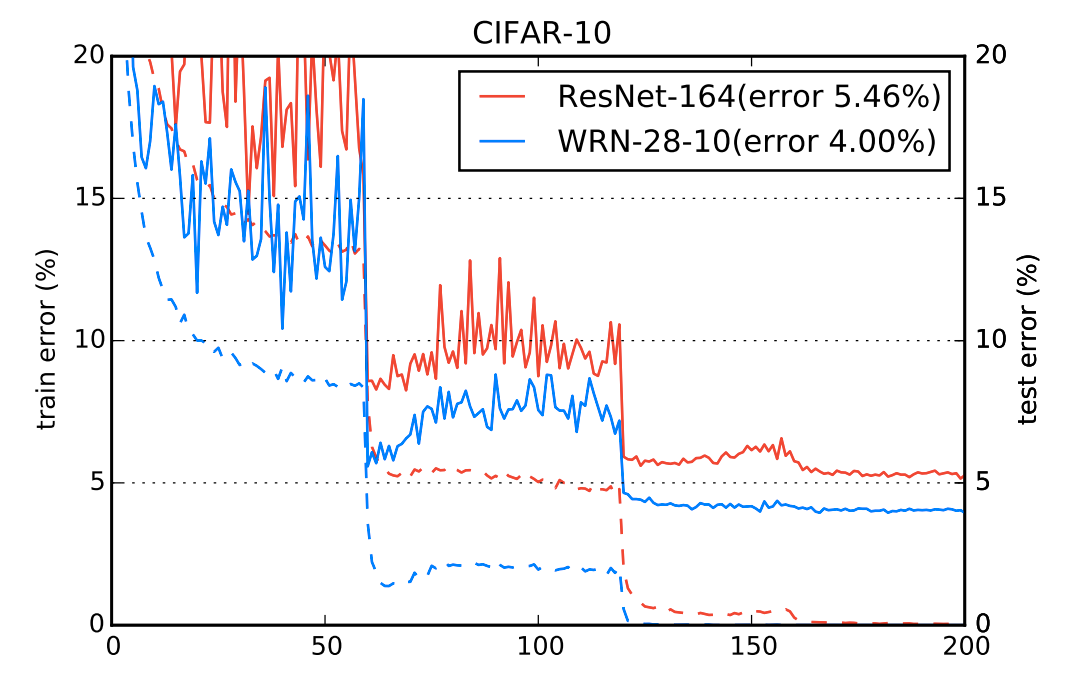
Zagoruyko et al. - Wide Residual Networks, 2016
Automatic methods
Existing methods:
- grid/random search
- Bayesian optimization
- evolutionary algorithms
Problem: non-parametric - can't transfer knowledge to new architectures/tasks.
Problem: hyperparameters typically fixed throughout training, or scheduled using parametric curves.
Possible benefit from adapting based on current metrics.
Solution: RL
Learn a policy for controlling hyperparameters based on the observed validation metrics.
Can train on a wide range of architectures and tasks.
Zero-shot or few-shot transfer to new architectures and tasks.
Long-term goal: a general system that can automatically tune anything.
Open-source the policies, so all ML practitioners can use them.
Adaptive tuning as a POMDP
Transition: a fixed number of training steps, followed by evaluation.
Observation :
- current metrics, e.g. training/validation accuracy/loss
- current hyperparameter values
Action : discrete; for every hyperparameter - increase/decrease by a fixed %, or keep the same.
Reward : the increase of a chosen metric since the last environment step.
Adaptive tuning as a POMDP
Partially observable: observing all parameter values is intractable.
Nondeterministic: random weight initialization and dataset permutation.
Tasks
- Transformer LM on LM1B language modelling dataset (1B words)
- Transformer LM on Penn Treebank language modelling dataset (3M words)
- Transformer LM on WMT EN -> DE translation dataset, framed as primed language modeling
- Wide ResNet on CIFAR-10 image classification dataset
Tuned hyperparameters
For Transformers:
- learning rate
- weight decay rate
- dropouts, separately for each layer
For Wide ResNet:
- learning rate
- weight decay rate
- momentum mass in SGD
Model-free approach: PPO
PPO: Proximal Policy Optimization
- stable
- more sample-efficient than vanilla policy gradient
- widely used
Use the Transformer language model without input embedding as a policy.
Schulman et al. - Proximal Policy Optimization Algorithms, 2017
Model-free approach: PPO
Experiment setup:
- optimizing for accuracy on a holdout set
- 20 PPO epochs
- 128 parallel model trainings in each epoch
- 4 repetitions of each experiment
- ~3h per model training, ~60h for the entire experiment
Model-free approach: PPO
some nice plots here
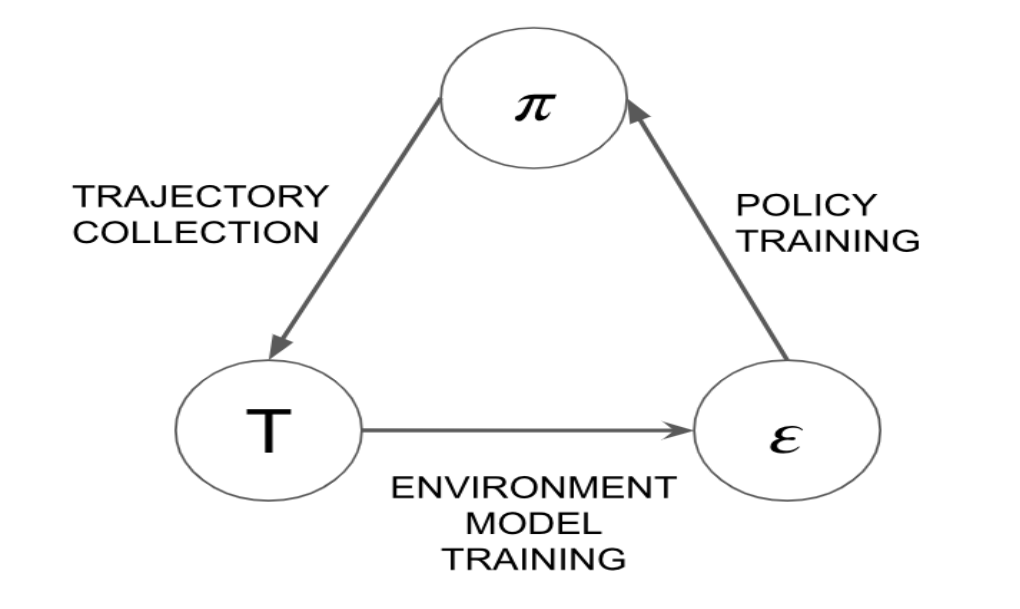
Model-based approach: SimPLe
SimPLe: Simulated Policy Learning
Elements:
- policy
- "world model"
Train the world model on data collected in the environment.
Train the policy using PPO in the environment simulated by the world model.
Much more sample-efficient than model-free PPO.
Kaiser et al. - Model-Based Reinforcement Learning for Atari, 2019
Model-based approach: SimPLe
Transformer language model
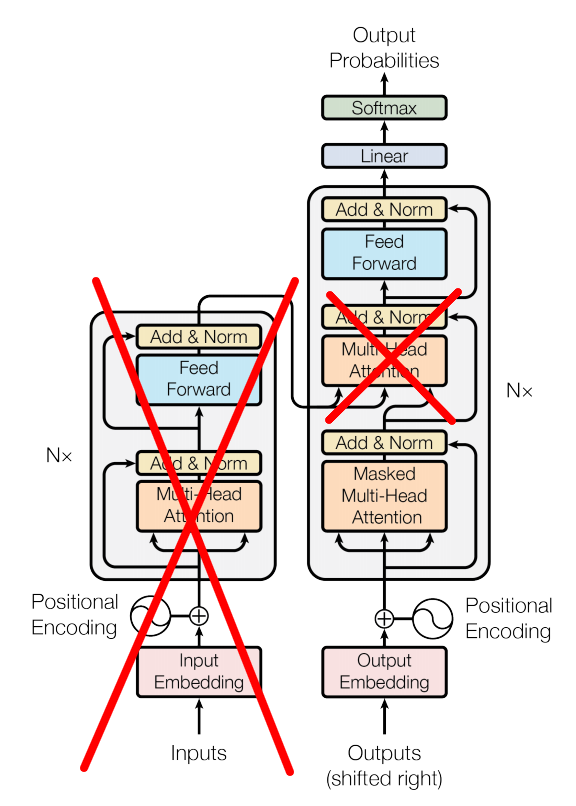
Vaswani et al. - Attention Is All You Need, 2017
Time series forecasting
The metric curves are stochastic.
Autoregressive factorization:
Typically, need to assume a distribution for
(e.g. Gaussian, mixture of Gaussians)
Time series forecasting
Using fixed-precision encoding, we can model any distribution within a set precision, using symbols per number, with symbols in the alphabet.
Loss: cross-entropy weighted by symbol significance .
Time series forecasting
Example: 2 numbers, base-8 encoding using 2 symbols.
Representable range: .
Precision: .
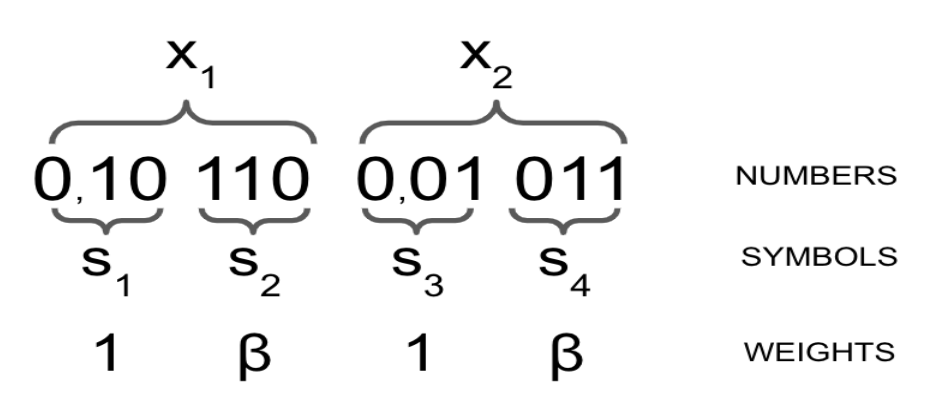
Time series forecasting
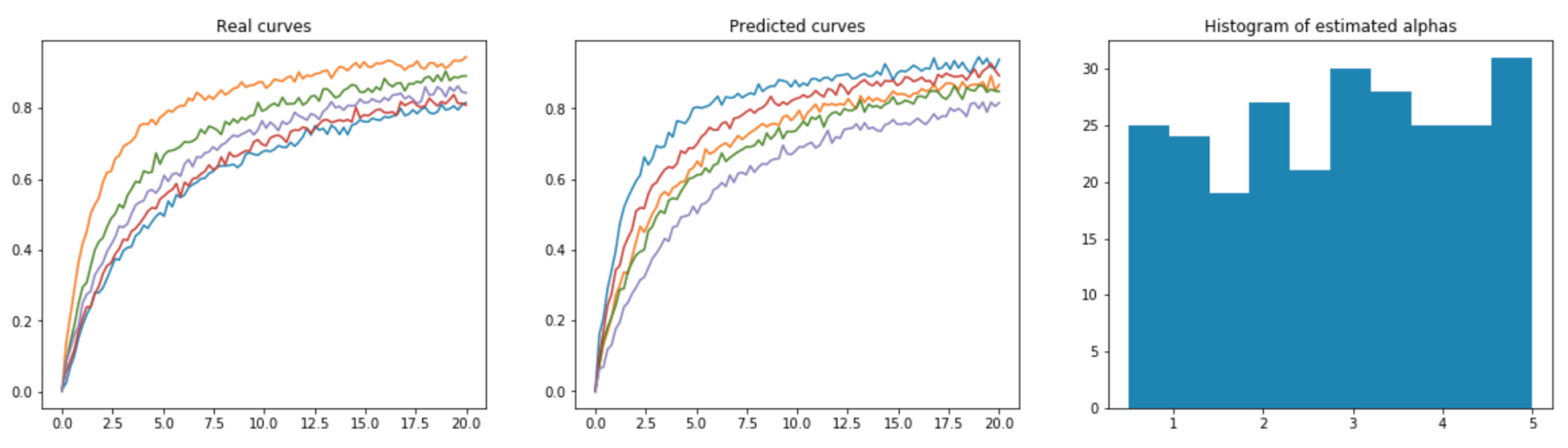
Experiment on synthetic data.
Data designed to mimic accuracy curves, converging to 1 at varying rates .
Parameter estimated back from generated curves:
Time series forecasting
Transformer as a world model
Modelled sequence:
Input: both observations and actions.
Predict only observations.
Rewards calculated based on the two last observations.
Transformer as a world model
Transformer as a policy
Share the architecture with the world model (also input embedding).
Input same as for the world model.
Output: action distribution, value estimate.
Action distribution independent with respect to each hyperparameter.
Transformer as a policy
Preinitialize from world model parameters.
This empirically works much better.
Intuition:
- symbol embeddings lose the inductive bias of continuousness
- attention masks need a lot of signal to converge
- reward signal noisy because of credit assignment
SimPLe results
Experiment setup:
- optimizing for accuracy on a holdout set
- starting from a dataset of 4 * 20 * 128 = 10240 trajectories collected in PPO experiments
- 10 SimPLe epochs
- 50 simulated PPO epochs in each SimPLe epoch
- 128 parallel model trainings in each data gathering phase
- 4 repetitions of each experiment
- ~3h for data gathering, ~1h for world model training, ~2h for policy training, ~60h for the entire experiment
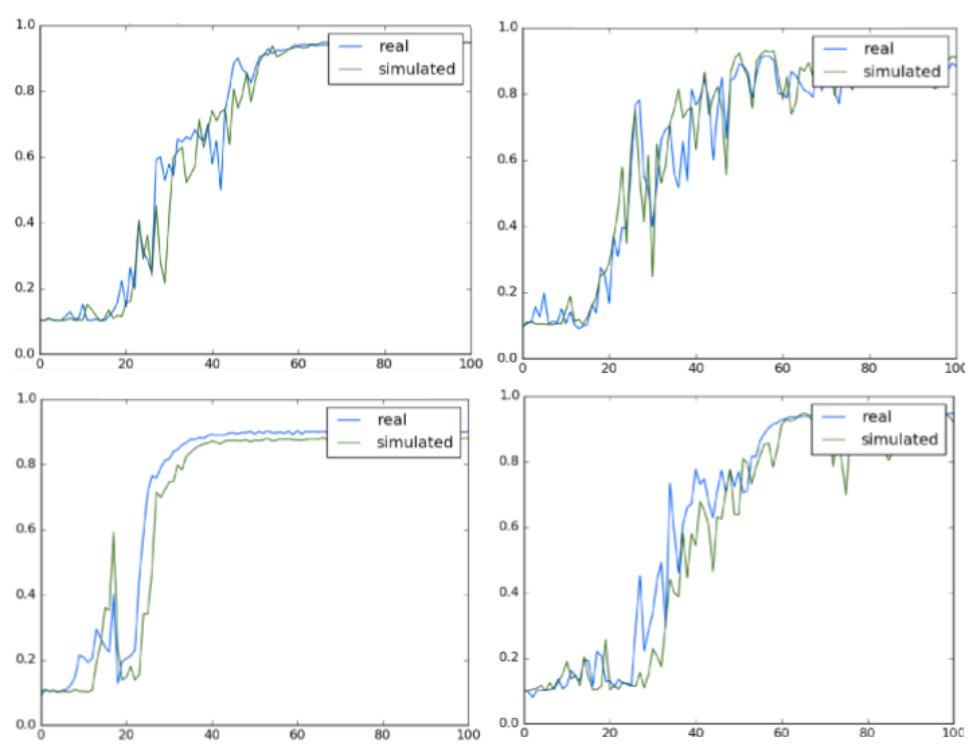
SimPLe results
some nice plots here
SimPLe vs PPO vs human
| task | SimPLe | PPO | human |
|---|---|---|---|
| LM1B | 0.35 | ||
| WMT EN -> DE | 0.595 | ||
| Penn Treebank | 0.168 | ||
| CIFAR-10 | 0.933 |
Final accuracies:
Summary and future work
Amount of data needed for now: ~11K model trainings.
Comparable to the first work in Neural Architecture Search.
Not practically applicable yet.
Future work:
- Policy or world model transfer across tasks to enable practical application.
- Evaluation in settings that are notoriously unstable (unsupervised/reinforcement learning); adaptive tuning should help.
Zoph et al. - Neural Architecture Search with Reinforcement Learning, 2016
Speaker: Piotr Kozakowski (p.kozakowski@mimuw.edu.pl)
Paper under review for ICLR 2020:
Forecasting Deep Learning Dynamics with Applications to Hyperparameter Tuning
References:
Zagoruyko et al. - Wide Residual Networks, 2016
Schulman et al. - Proximal Policy Optimization Algorithms, 2017
Kaiser et al. - Model-Based Reinforcement Learning for Atari, 2019
Vaswani et al. - Attention Is All You Need, 2017
Zoph et al. - Neural Architecture Search with Reinforcement Learning, 2016