Phase-Type  Models in
Life Insurance

Dr Patrick J. Laub

Université Lyon 1

https://slides.com/plaub/l2

t
X_t

Example Markov process 

( X_t )_{t \ge 0}

Sojourn times

Sojourn times are the random lengths of time spent in each state

S_1
S_2
S_3
S_5^{(1)}
S_5^{(2)}
S_1 \sim \mathsf{Exp}(1/\mu_1)
S_2 \sim \mathsf{Exp}(1/\mu_2)
S_5^{(1)}, S_5^{(2)} \overset{\mathrm{i.i.d.}}{\sim} \mathsf{Exp}(1/\mu_5)
S_4

Phase-type definition

Markov process                             State space

 

 

 

 

 

  • Initial distribution
     
  • Sub-transition matrix
     
  • Exit rates

 

\boldsymbol{\alpha}
\boldsymbol{T}
\boldsymbol{t} = -\boldsymbol{T} 1
\boldsymbol{t}
\tau = \inf_t \{ X_t = \dagger \}
( X_t )_{t \ge 0}
\{1, ..., p, \dagger \}
\Leftrightarrow \tau \sim \mathrm{PhaseType}(\boldsymbol{\alpha}, \boldsymbol{T})
\boldsymbol{Q} = \begin{bmatrix} \boldsymbol{T} & \boldsymbol{t} \\ 0 & 0 \end{bmatrix}
\dagger
1
3
2
\boldsymbol{Q} = \begin{bmatrix} -6 & 4 & 2 & 0 \\ 1 & -1 & 0 & 0 \\ 0 & 5 & -5.5 & 0.5 \\ 0 & 0 & 0 & 0 \end{bmatrix}
\boldsymbol{\alpha} = [ \frac13, \frac13, \frac13, 0 ]^\top
2
4
1
0.5
5

Example

Markov process                             State space

( X_t )_{t \ge 0}
\{1, 2, 3, \dagger \}
\boldsymbol{T} = \begin{bmatrix} -6 & 4 & 2 \\ 1 & -1 & 0 \\ 0 & 5 & -5.5 \end{bmatrix}
\boldsymbol{t} = \begin{bmatrix} 0 \\ 0 \\ 0.5 \end{bmatrix}

Phase-type generalises...

  • Exponential distribution


     
  • Sums of exponentials (Erlang distribution)




     
  • Mixtures of exponentials (hyperexponential distribution)
\boldsymbol{\alpha} = [ 1 ], \boldsymbol{T} = [ -\lambda ], \boldsymbol{t} = [ \lambda ]
\boldsymbol{\alpha} = \begin{bmatrix} 1 \\ 0 \\ 0 \end{bmatrix} , \boldsymbol{T} = \begin{bmatrix} -\lambda_1 & \lambda_1 & 0 \\ 0 & -\lambda_2 & \lambda_2 \\ 0 & 0 & -\lambda_3 \end{bmatrix} , \boldsymbol{t} = \begin{bmatrix} 0 \\ 0 \\ \lambda_3 \end{bmatrix}
\boldsymbol{\alpha} = \begin{bmatrix} \alpha_1 \\ \alpha_2 \\ \alpha_3 \end{bmatrix} , \boldsymbol{T} = \begin{bmatrix} -\lambda_1 & 0 & 0 \\ 0 & -\lambda_2 & 0 \\ 0 & 0 & -\lambda_3 \end{bmatrix} , \boldsymbol{t} = \begin{bmatrix} \lambda_1 \\ \lambda_2 \\ \lambda_3 \end{bmatrix}

Phase-type properties

 

 

Matrix exponential

 

Density and tail

 

 

Moments

 

 

Laplace transform

f_\tau(s) = \boldsymbol{\alpha}^\top \mathrm{e}^{\boldsymbol{T} s} \boldsymbol{t}
\mathrm{e}^{\boldsymbol{T} s} = \sum_{i=0}^\infty \frac{(\boldsymbol{T} s)^i}{i!}
\tau \sim \mathrm{PhaseType}(\boldsymbol{\alpha}, \boldsymbol{T})
\overline{F}_\tau(s) = \boldsymbol{\alpha}^\top \mathrm{e}^{\boldsymbol{T} s} 1
\mathbb{E}[\tau] = {-}\boldsymbol{\alpha}^\top \boldsymbol{T}^{-1} \boldsymbol{1}
\mathbb{E}[\tau^n] = (-1)^n n! \,\, \boldsymbol{\alpha}^\top \boldsymbol{T}^{-n} \boldsymbol{1}
\mathbb{E}[\mathrm{e}^{-s\tau}] = \boldsymbol{\alpha}^\top (s \boldsymbol{I} - \boldsymbol{T})^{-1} \boldsymbol{t}

More cool properties

Closure under addition, minimum, maximum

(\tau \mid \tau > s) \sim \mathrm{PhaseType}(\boldsymbol{\alpha}_s, \boldsymbol{T})
\tau_i \overset{\mathrm{ind.}}{\sim} \mathrm{PhaseType}(\boldsymbol{\alpha}_i, \boldsymbol{T}_i)
\Rightarrow \tau_1 + \tau_2 \sim \mathrm{PhaseType}(\dots, \dots)
\Rightarrow \min\{ \tau_1 , \tau_2 \} \sim \mathrm{PhaseType}(\dots, \dots)

... and under conditioning

\Rightarrow \max\{ \tau_1 , \tau_2 \} \sim \mathrm{PhaseType}(\dots, \dots)

When to use phase-type?

Your problem has "flowchart" structure.

\boldsymbol{\alpha} = \begin{bmatrix} 1 \\ 0 \\ 0 \\ \vdots \end{bmatrix} , \quad \boldsymbol{T} = \begin{bmatrix} -t_{11} & t_{12} & 0 & \\ 0 & -t_{22} & t_{23} & \dots\\ 0 & 0 & -t_{33} & \\ & \vdots & & \ddots \end{bmatrix} , \quad \boldsymbol{t} = \begin{bmatrix} t_1 \\ t_2 \\ t_3 \\ \vdots \end{bmatrix}

"Coxian distribution"

"Calendar" Age

"Physical" age

X.S. Lin & X. Liu (2007) ,  M. Govorun, G. Latouche, & S. Loisel (2015).

Class of phase-types is dense

S. Asmussen (2003), Applied Probability and Queues, 2nd Edition, Springer

Class of phase-types is dense

p = 1
\text{Target}
p = 10
p = 25
p = 50
p = 100
p = 150
p = 200
p = 250
p = 300
\tau
S_t
t

Guaranteed Minimum Death Benefit

S_\tau
\text{Payoff} = \max( S_{\tau}, K )

Application

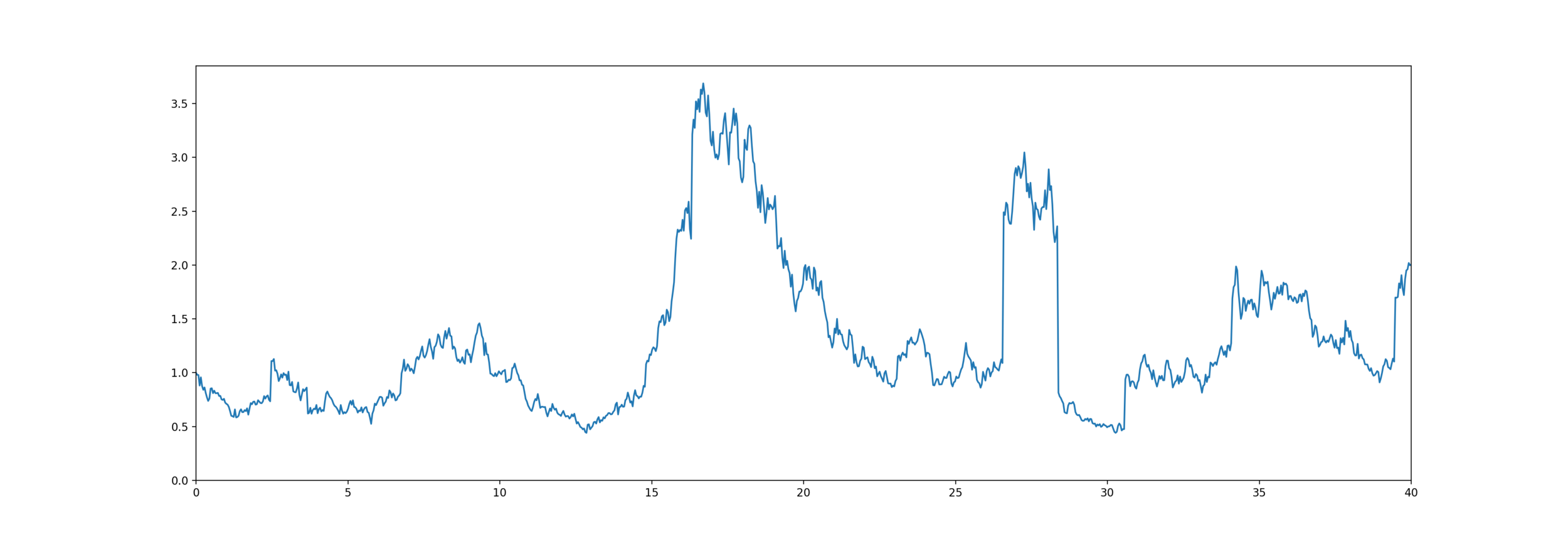
​Equity-linked life insurance

\tau
t

High Water Death Benefit

\text{Payoff} = \overline{S}_{\tau}

Equity-linked life insurance

\overline{S}_\tau
\overline{S}_t = \max_{s \le t} S_s

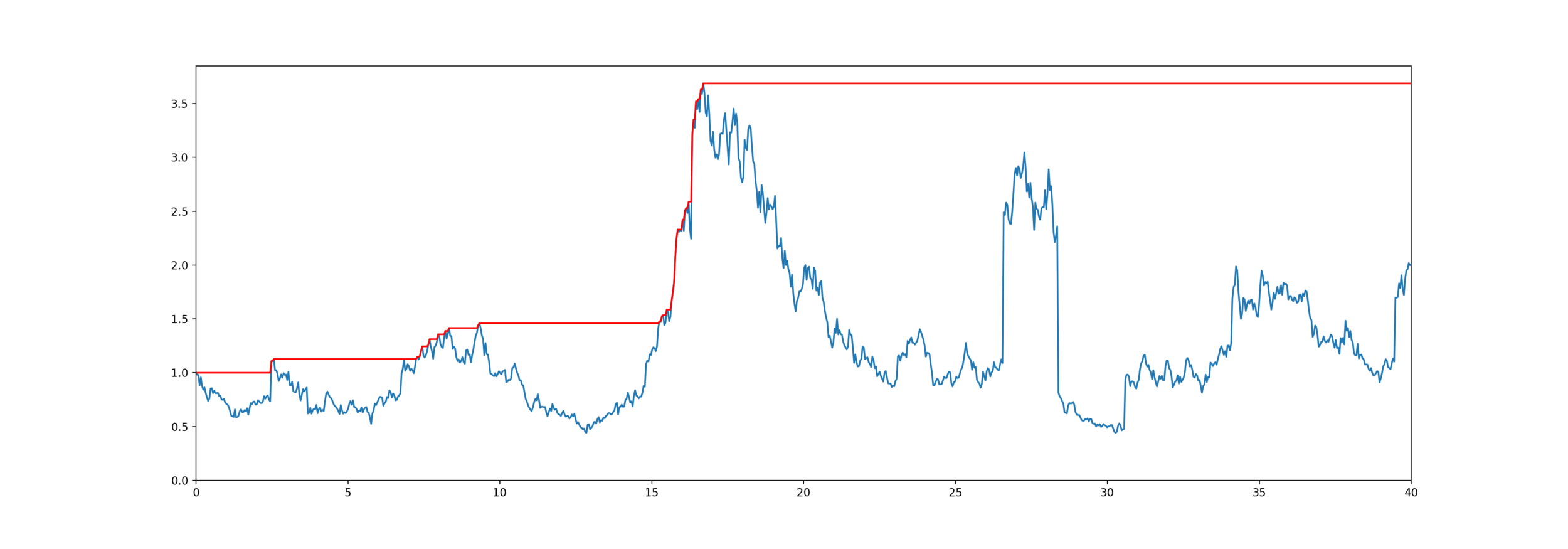
Model for mortality and equity

The customer lives for         years, 

\tau
\tau \sim \text{PhaseType}(\boldsymbol{\alpha}, \boldsymbol{T})
X_t \sim \text{Jump Diffusion}
S_t = S_0 \mathrm{e}^{X_t}

The stock price is an exponential jump diffusion,

\text{Brownian Motion}(\mu, \sigma^2) + \text{Compound Poisson}(\lambda_1) + \text{Compound Poisson}(\lambda_2)
\text{Price} = \mathbb{E}[ \mathrm{e}^{-\delta \tau} \text{Payoff}( S_\tau, \overline{S}_\tau ) ]
S_t
t

Exponential PH-Jump Diffusion

\text{UpJumpSize}_i \overset{\mathrm{i.i.d.}}{\sim} \text{PhaseType}(\boldsymbol{\alpha}_1, \boldsymbol{T}_1)
\text{DownJumpSize}_i \overset{\mathrm{i.i.d.}}{\sim} \text{PhaseType}(\boldsymbol{\alpha}_2, \boldsymbol{T}_2)
f(s) = \boldsymbol{\alpha}^\top \mathrm{e}^{\boldsymbol{T} s} \boldsymbol{t}

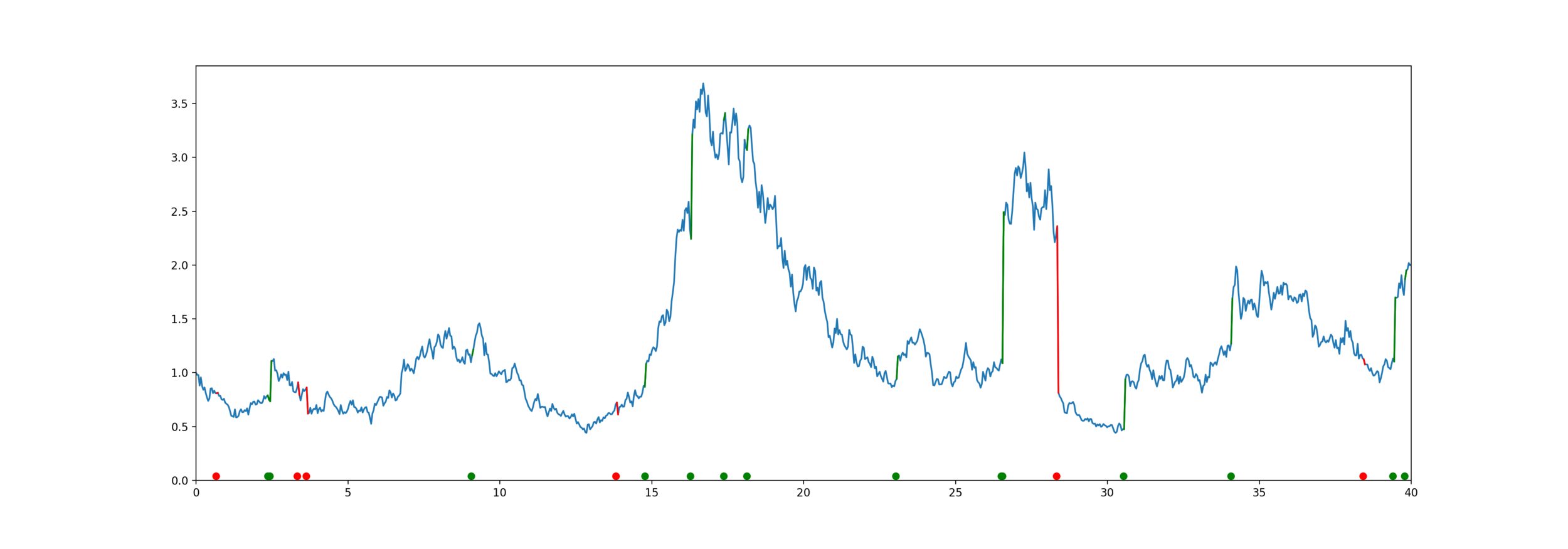
How to fit them?

\mathrm{e}^{\boldsymbol{T} s} = \sum_{i=0}^\infty \frac{(\boldsymbol{T} s)^i}{i!}
\boldsymbol{\tau} = [\tau_1, \tau_2, \dots, \tau_n]

Observations:

L( \boldsymbol{\alpha} , \boldsymbol{T} \mid \boldsymbol{\tau} ) = \prod_{i=1}^n \boldsymbol{\alpha}^\top \mathrm{e}^{\boldsymbol{T} \tau_i} \boldsymbol{t}

Derivatives?

\ell( \boldsymbol{\alpha} , \boldsymbol{T} \mid \boldsymbol{\tau} ) = \sum_{i=1}^n \log\Bigl\{ \boldsymbol{\alpha}^\top \left[ \sum_{j=0}^\infty \frac{(\boldsymbol{T} \tau_i)^j}{j!} \right] \boldsymbol{t} \Bigr\}

Model (p.d.f.):

How to fit them?

\begin{aligned} L( \boldsymbol{\alpha} , \boldsymbol{T} \mid \boldsymbol{B}, \boldsymbol{Z}, \boldsymbol{N} ) &= \prod_{i=1}^p \alpha_i^{B_i} \prod_{i=1}^p \mathrm{e}^{-t_{ii} Z_i } \prod_{i,j \text{ combs}} t_{ij}^{N_{ij}} \\ \end{aligned}

Hidden values:

\(B_i\) number of MC's starting in state \(i\)

\(Z_i\) total time spend in state \(i\)

\(N_{ij}\) number of transitions from state \(i\) to \(j\)

\boldsymbol{T} = \begin{bmatrix} -t_{11} & t_{12} & t_{13} \\ t_{21} & -t_{22} & t_{23} \\ t_{31} & t_{32} & -t_{33} \end{bmatrix}
\widehat{\alpha}_i = \frac{B_i}{n}
\widehat{t}_{i} = \frac{N_{i\dagger}}{Z_i}
\boldsymbol{t} = \begin{bmatrix} t_1 \\ t_2 \\ t_3 \end{bmatrix}
\boldsymbol{\alpha} = \begin{bmatrix} \alpha_1 \\ \alpha_2 \\ \alpha_3 \end{bmatrix}
\widehat{t}_{ij} = \frac{N_{ij}}{Z_i}

C to Julia

void rungekutta(int p, double *avector, double *gvector, double *bvector,
		double **cmatrix, double dt, double h, double **T, double *t,
		double **ka, double **kg, double **kb, double ***kc)
{
  int i, j, k, m;
  double eps, h2, sum;

  i = dt/h;
  h2 = dt/(i+1);
  init_matrix(ka, 4, p);
  init_matrix(kb, 4, p);
  init_3dimmatrix(kc, 4, p, p);
  if (kg != NULL)
    init_matrix(kg, 4, p);
    ...
    for (i=0; i < p; i++) {
      avector[i] += (ka[0][i]+2*ka[1][i]+2*ka[2][i]+ka[3][i])/6;
      bvector[i] += (kb[0][i]+2*kb[1][i]+2*kb[2][i]+kb[3][i])/6;
      for (j=0; j < p; j++)
        cmatrix[i][j] +=(kc[0][i][j]+2*kc[1][i][j]+2*kc[2][i][j]+kc[3][i][j])/6;
    }
  }
}

This function: 116 lines of C, built-in to Julia

Whole program: 1700 lines of C, 300 lines of Julia 

# Run the ODE solver.
u0 = zeros(p*p)
pf = ParameterizedFunction(ode_observations!, fit)
prob = ODEProblem(pf, u0, (0.0, maximum(s.obs)))
sol = solve(prob, OwrenZen5())

https://github.com/Pat-Laub/EMpht.jl

Lots of parameters to fit

  • General




     
  • Coxian distribution
\boldsymbol{\alpha} = \begin{bmatrix} 1 \\ 0 \\ 0 \end{bmatrix} , \quad \boldsymbol{T} = \begin{bmatrix} -t_{11} & t_{12} & 0 \\ 0 & -t_{22} & t_{23} \\ 0 & 0 & -t_{33} \end{bmatrix} , \quad \boldsymbol{t} = \begin{bmatrix} t_1 \\ t_2 \\ t_{33} \end{bmatrix}
\boldsymbol{\alpha} = \begin{bmatrix} \alpha_1 \\ \alpha_2 \\ \alpha_3 \end{bmatrix} , \quad \boldsymbol{T} = \begin{bmatrix} -t_{11} & t_{12} & t_{13} \\ t_{21} & -t_{22} & t_{23} \\ t_{31} & t_{32} & -t_{33} \end{bmatrix} , \quad \boldsymbol{t} = \begin{bmatrix} t_1 \\ t_2 \\ t_3 \end{bmatrix}
p^2 + (p-1)
p + (p-1)

In general, representation is not unique

A twist on the Coxian form

Canonical form 1

t_{11} < t_{22} < \dots < t_{pp}
\boldsymbol{\alpha} = \begin{bmatrix} \alpha_1 \\ \alpha_2 \\ \alpha_3 \end{bmatrix} , \quad \boldsymbol{T} = \begin{bmatrix} -t_{11} & t_{11} & 0 \\ 0 & -t_{22} & t_{22} \\ 0 & 0 & -t_{33} \end{bmatrix} , \quad \boldsymbol{t} = \begin{bmatrix} 0 \\ 0 \\ t_{33} \end{bmatrix}

Problem: to model mortality via phase-type

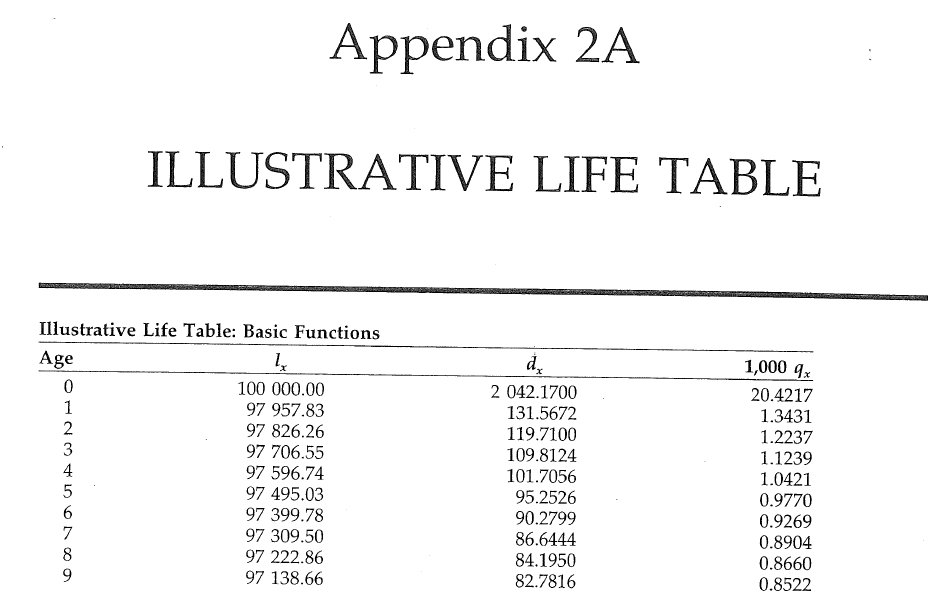
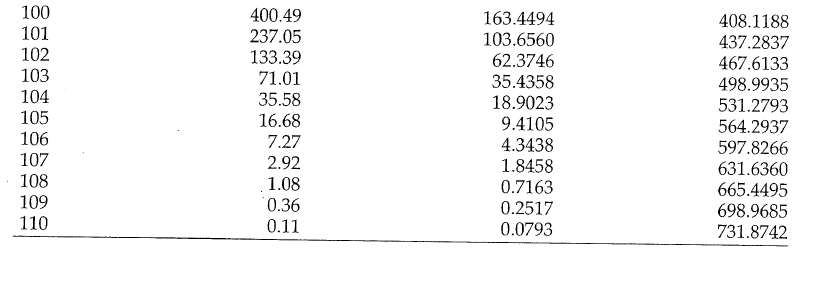
Bowers et al (1997), Actuarial Mathematics, 2nd Edition

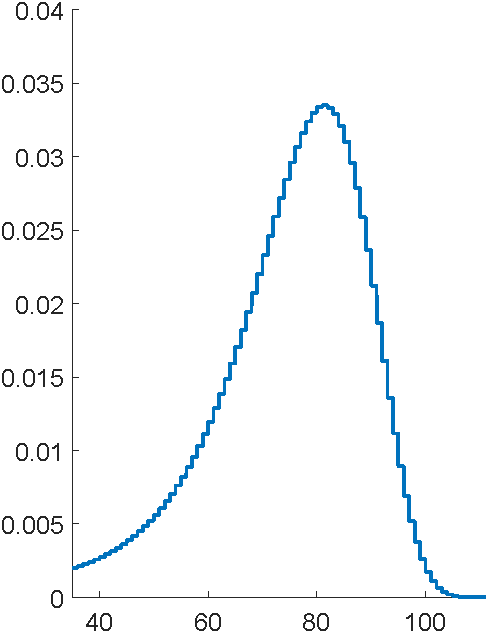
Final fit

p = 200
\text{Life Table}
using Pkg
using EMpht

lt = EMpht.parse_settings("life_table.json")[1]
phCF200 = empht(lt, p=200, ph_structure="CanonicalForm1")

Heavy-tailed modeling?

Phase-types are always light-tailed

Can 'splice' together a Franken-distribution

Norwegian fire data

Take logarithms

\tau_i = \log( X_i ) \sim \mathrm{PhaseType}(\boldsymbol{\alpha}, \boldsymbol{T} )

Take logarithms and shift

\tau_i = \log( X_i ) - c \sim \mathrm{PhaseType}(\boldsymbol{\alpha}, \boldsymbol{T} )
logClaims = log.(claims)
logClaimsCentered = logClaims .- minimum(logClaims) .+ 1e-4

~, int, intweight = bin_observations(logClaimsCentered, 500)
sInt = EMpht.Sample(int=int, intweight=intweight)

ph = empht(sInt, p=5)
logClaims = log.(claims)
logClaimsCentered = logClaims .- minimum(logClaims) .+ 1e-4

~, int, intweight = bin_observations(logClaimsCentered, 500)
sInt = EMpht.Sample(int=int, intweight=intweight)

ph = empht(sInt, p=40)

Take logarithms and shift

\tau_i = \log( X_i ) - c \sim \mathrm{PhaseType}(\boldsymbol{\alpha}, \boldsymbol{T} )

Questions?

https://slides.com/plaub/l2

Why does that work?

\tau_n \sim \mathrm{Erlang}(n, n/T) \,, \quad \tau_n \approx T

Can make a phase-type look like a constant value

Made with Slides.com