Phase-Type  Models in
Life Insurance

Dr Patrick J. Laub @ PARTY, Sibiu

https://slides.com/plaub/party-talk/

Motivating theory

Stochastic Models (2019), 34(4), 1-12.

Can read on https://arxiv.org/pdf/1803.00273.pdf

τ\tau
\tau
StS_t
S_t
tt
t

Guaranteed Minimum Death Benefit

SτS_\tau
S_\tau
Payoff=max⁡(Sτ,K)\text{Payoff} = \max( S_{\tau}, K )
\text{Payoff} = \max( S_{\tau}, K )

Equity-linked life insurance

τ\tau
\tau
tt
t

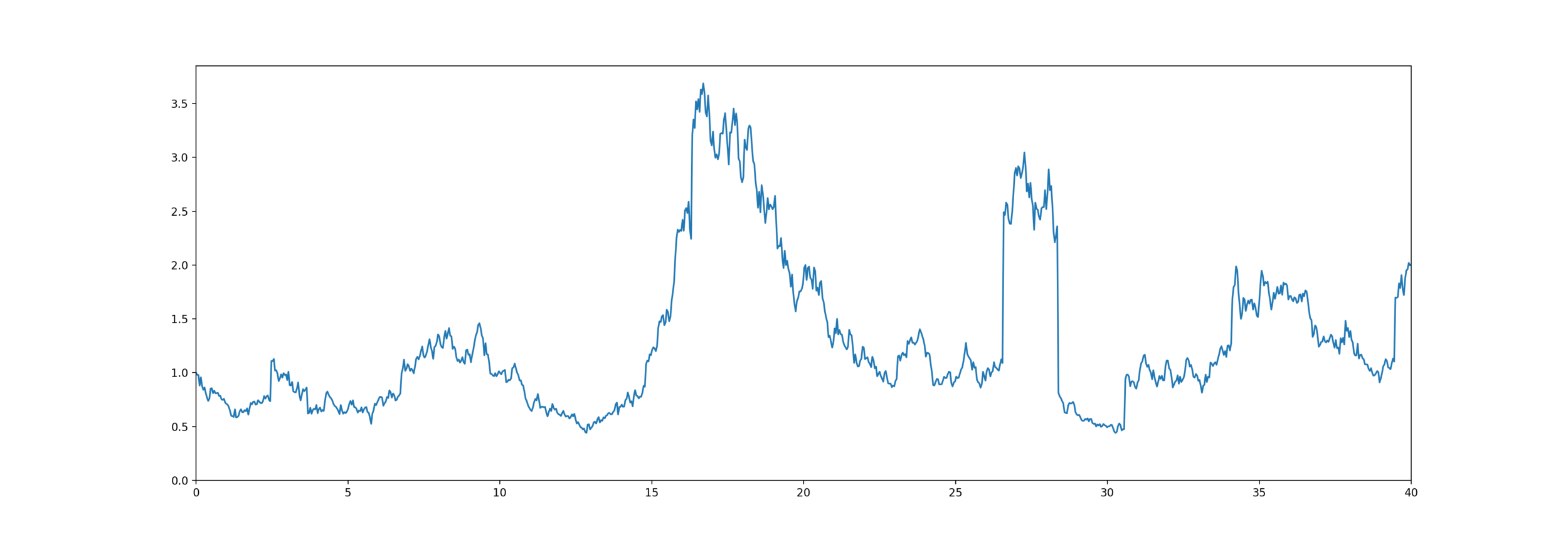
High Water Death Benefit

Payoff=S‾τ\text{Payoff} = \overline{S}_{\tau}
\text{Payoff} = \overline{S}_{\tau}

Equity-linked life insurance

S‾τ\overline{S}_\tau
\overline{S}_\tau
S‾t=max⁡s≤tSs\overline{S}_t = \max_{s \le t} S_s
\overline{S}_t = \max_{s \le t} S_s

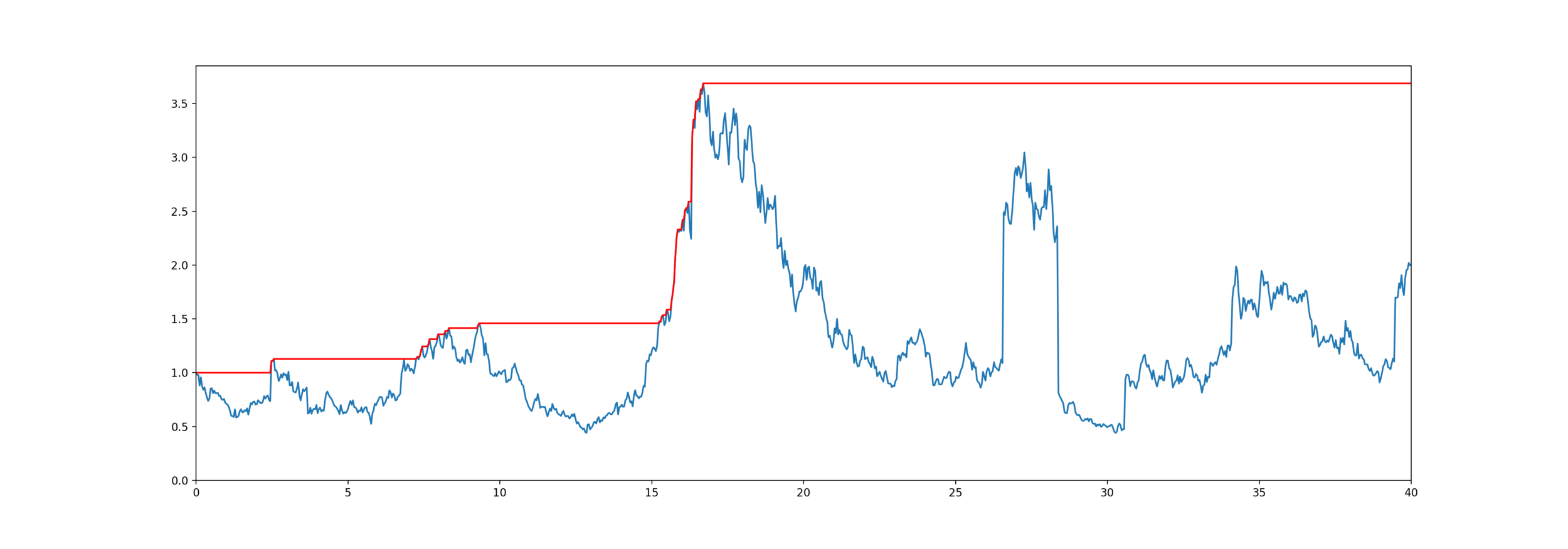
Model for mortality and equity

The customer lives for         years, 

τ\tau
\tau
τ∼PhaseType(α,T)\tau \sim \text{PhaseType}(\boldsymbol{\alpha}, \boldsymbol{T})
\tau \sim \text{PhaseType}(\boldsymbol{\alpha}, \boldsymbol{T})
Xt∼Jump DiffusionX_t \sim \text{Jump Diffusion}
X_t \sim \text{Jump Diffusion}
St=S0eXtS_t = S_0 \mathrm{e}^{X_t}
S_t = S_0 \mathrm{e}^{X_t}

Equity is an exponential jump diffusion,

Brownian Motion(μ,σ2)+Compound Poisson(λ1)+Compound Poisson(λ2)\text{Brownian Motion}(\mu, \sigma^2) + \text{Compound Poisson}(\lambda_1) + \text{Compound Poisson}(\lambda_2)
\text{Brownian Motion}(\mu, \sigma^2) + \text{Compound Poisson}(\lambda_1) + \text{Compound Poisson}(\lambda_2)
Price=E[e−δτPayoff(Sτ,S‾τ)]\text{Price} = \mathbb{E}[ \mathrm{e}^{-\delta \tau} \text{Payoff}( S_\tau, \overline{S}_\tau ) ]
\text{Price} = \mathbb{E}[ \mathrm{e}^{-\delta \tau} \text{Payoff}( S_\tau, \overline{S}_\tau ) ]
StS_t
S_t
tt
t

Exponential PH-Jump Diffusion

UpJumpSizei∼i.i.d.PhaseType(α1,T1)\text{UpJumpSize}_i \overset{\mathrm{i.i.d.}}{\sim} \text{PhaseType}(\boldsymbol{\alpha}_1, \boldsymbol{T}_1)
\text{UpJumpSize}_i \overset{\mathrm{i.i.d.}}{\sim} \text{PhaseType}(\boldsymbol{\alpha}_1, \boldsymbol{T}_1)
DownJumpSizei∼i.i.d.PhaseType(α2,T2)\text{DownJumpSize}_i \overset{\mathrm{i.i.d.}}{\sim} \text{PhaseType}(\boldsymbol{\alpha}_2, \boldsymbol{T}_2)
\text{DownJumpSize}_i \overset{\mathrm{i.i.d.}}{\sim} \text{PhaseType}(\boldsymbol{\alpha}_2, \boldsymbol{T}_2)
#UpJumps(0,t)∼Poisson(λ1t)\# \text{UpJumps}(0, t) \sim \mathrm{Poisson}(\lambda_1 t)
\# \text{UpJumps}(0, t) \sim \mathrm{Poisson}(\lambda_1 t)
#DownJumps(0,t)∼Poisson(λ2t)\# \text{DownJumps}(0, t) \sim \mathrm{Poisson}(\lambda_2 t)
\# \text{DownJumps}(0, t) \sim \mathrm{Poisson}(\lambda_2 t)

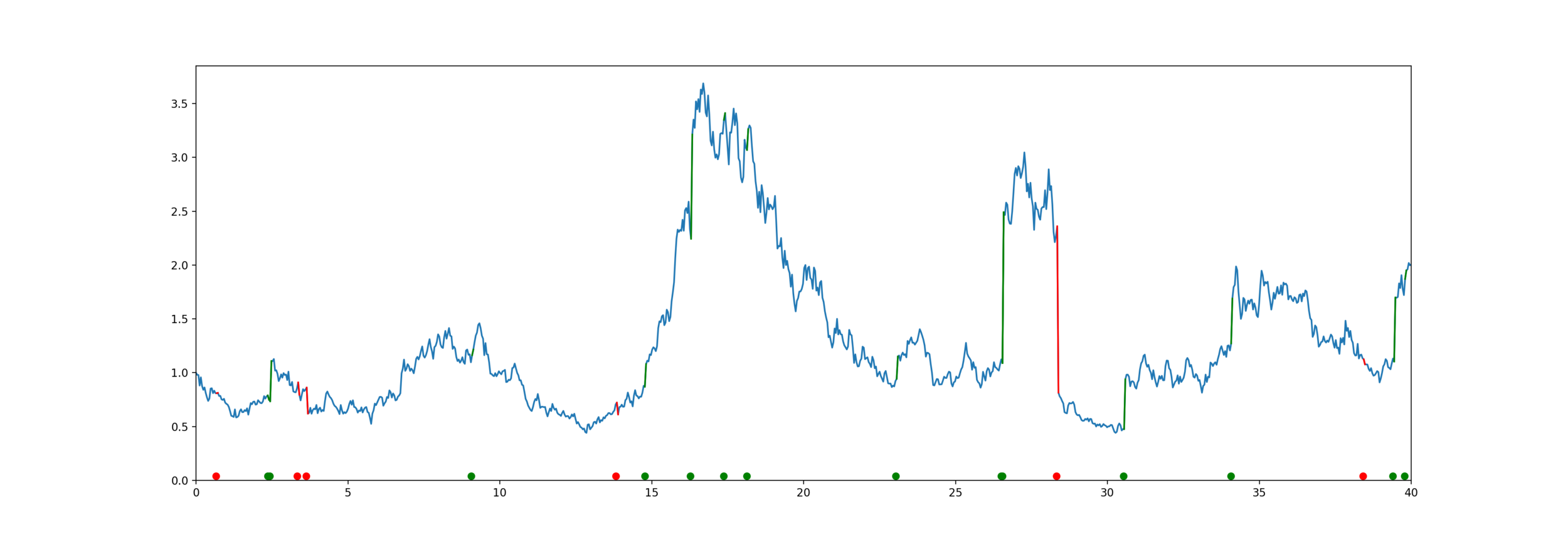
Get some helpful matrices

U=U(δ,μ,σ2,α,T,λ1,α1,T1,λ2,α2,T2)\boldsymbol{U} = \boldsymbol{U}(\delta, \mu, \sigma^2, \boldsymbol{\alpha}, \boldsymbol{T}, \lambda_1, \boldsymbol{\alpha}_1, \boldsymbol{T}_1, \lambda_2, \boldsymbol{\alpha}_2, \boldsymbol{T}_2 )
\boldsymbol{U} = \boldsymbol{U}(\delta, \mu, \sigma^2, \boldsymbol{\alpha}, \boldsymbol{T}, \lambda_1, \boldsymbol{\alpha}_1, \boldsymbol{T}_1, \lambda_2, \boldsymbol{\alpha}_2, \boldsymbol{T}_2 )
UpJumpSizei∼i.i.d.PhaseType(α1,T1)\text{UpJumpSize}_i \overset{\mathrm{i.i.d.}}{\sim} \text{PhaseType}({ \color{red} \boldsymbol{\alpha}_1 }, { \color{red} \boldsymbol{T}_1 })
\text{UpJumpSize}_i \overset{\mathrm{i.i.d.}}{\sim} \text{PhaseType}({ \color{red} \boldsymbol{\alpha}_1 }, { \color{red} \boldsymbol{T}_1 })
DownJumpSizei∼i.i.d.PhaseType(α2,T2)\text{DownJumpSize}_i \overset{\mathrm{i.i.d.}}{\sim} \text{PhaseType}( { \color{red} \boldsymbol{\alpha}_2 }, { \color{red} \boldsymbol{T}_2 })
\text{DownJumpSize}_i \overset{\mathrm{i.i.d.}}{\sim} \text{PhaseType}( { \color{red} \boldsymbol{\alpha}_2 }, { \color{red} \boldsymbol{T}_2 })
#UpJumps(0,t)∼Poisson(λ1t)\# \text{UpJumps}(0, t) \sim \mathrm{Poisson}({ \color{red} \lambda_1 } t)
\# \text{UpJumps}(0, t) \sim \mathrm{Poisson}({ \color{red} \lambda_1 } t)
#DownJumps(0,t)∼Poisson(λ2t)\# \text{DownJumps}(0, t) \sim \mathrm{Poisson}({ \color{red} \lambda_2 } t)
\# \text{DownJumps}(0, t) \sim \mathrm{Poisson}({ \color{red} \lambda_2 } t)
Brownian Motion(μ,σ2)\text{Brownian Motion}({ \color{red} \mu }, { \color{red} \sigma^2 })
\text{Brownian Motion}({ \color{red} \mu }, { \color{red} \sigma^2 })
τ∼PhaseType(α,T)\tau \sim \text{PhaseType}({ \color{red} \boldsymbol{\alpha} }, { \color{red} \boldsymbol{T} })
\tau \sim \text{PhaseType}({ \color{red} \boldsymbol{\alpha} }, { \color{red} \boldsymbol{T} })
Price=E[e−δτPayoff(Sτ,S‾τ)]\text{Price} = \mathbb{E}[ \mathrm{e}^{-{\color{red} \delta} \tau} \text{Payoff}( S_\tau, \overline{S}_\tau ) ]
\text{Price} = \mathbb{E}[ \mathrm{e}^{-{\color{red} \delta} \tau} \text{Payoff}( S_\tau, \overline{S}_\tau ) ]
Un+1=f(Un)\boldsymbol{U}_{n+1} = f(\boldsymbol{U}_n)
\boldsymbol{U}_{n+1} = f(\boldsymbol{U}_n)

Use fixed-point approximation

U∗=U∗(δ,μ,σ2,α,T,λ1,α1,T1,λ2,α2,T2)\boldsymbol{U}^* = \boldsymbol{U}^*(\delta, \mu, \sigma^2, \boldsymbol{\alpha}, \boldsymbol{T}, \lambda_1, \boldsymbol{\alpha}_1, \boldsymbol{T}_1, \lambda_2, \boldsymbol{\alpha}_2, \boldsymbol{T}_2 )
\boldsymbol{U}^* = \boldsymbol{U}^*(\delta, \mu, \sigma^2, \boldsymbol{\alpha}, \boldsymbol{T}, \lambda_1, \boldsymbol{\alpha}_1, \boldsymbol{T}_1, \lambda_2, \boldsymbol{\alpha}_2, \boldsymbol{T}_2 )
Un+1∗=f∗(Un∗)\boldsymbol{U}_{n+1}^* = f^*(\boldsymbol{U}_n^*)
\boldsymbol{U}_{n+1}^* = f^*(\boldsymbol{U}_n^*)

We're starting to some library to do this more generally

Pricing these contracts

Price=E[e−δτPayoff(Sτ,S‾τ)]\text{Price} = \mathbb{E}[ \mathrm{e}^{-\delta \tau} \text{Payoff}( S_\tau, \overline{S}_\tau ) ]
\text{Price} = \mathbb{E}[ \mathrm{e}^{-\delta \tau} \text{Payoff}( S_\tau, \overline{S}_\tau ) ]
Price=α⊤F diag(r) G α∗\text{Price} = \boldsymbol{\alpha}^\top \boldsymbol{F} \, \text{diag}(\boldsymbol{r}) \, \boldsymbol{G} \, \boldsymbol{\alpha}^*
\text{Price} = \boldsymbol{\alpha}^\top \boldsymbol{F} \, \text{diag}(\boldsymbol{r}) \, \boldsymbol{G} \, \boldsymbol{\alpha}^*
G=G(g,U∗)\boldsymbol{G} = \boldsymbol{G}(g, \boldsymbol{U}^*)
\boldsymbol{G} = \boldsymbol{G}(g, \boldsymbol{U}^*)
F=F(f,U)\boldsymbol{F} = \boldsymbol{F}(f, \boldsymbol{U})
\boldsymbol{F} = \boldsymbol{F}(f, \boldsymbol{U})
Payoff(Sτ,S‾τ)=f(Sτ)g(S‾τ)\text{Payoff}(S_\tau, \overline{S}_\tau) = f(S_\tau) g(\overline{S}_\tau)
\text{Payoff}(S_\tau, \overline{S}_\tau) = f(S_\tau) g(\overline{S}_\tau)
r=r(U,U∗)\boldsymbol{r} = \boldsymbol{r}( \boldsymbol{U}, \boldsymbol{U}^* )
\boldsymbol{r} = \boldsymbol{r}( \boldsymbol{U}, \boldsymbol{U}^* )
α∗=(−T1)⊤diag(−αT)\boldsymbol{\alpha}^* = (-\boldsymbol{T} \boldsymbol{1}) ^{\top} \text{diag}(-\boldsymbol{\alpha} \boldsymbol{T})
\boldsymbol{\alpha}^* = (-\boldsymbol{T} \boldsymbol{1}) ^{\top} \text{diag}(-\boldsymbol{\alpha} \boldsymbol{T})

Take home messages

  • If you really care about equity-linked life insurance, check out our paper
  • What are phase-type distributions?
  • Why are they cool?
  • Strategy: if some maths works when using an exponential distribution, try a phase-type distribution
  • I have a package to fit them in Julia
  • If you've never tried it, check out Julia language.
†\dagger
\dagger
11
1
33
3
22
2
T‾=(−64201−10005−5.50.50000)\overline{\boldsymbol{T}} = \left( \begin{matrix} -6 & 4 & 2 & 0 \\ 1 & -1 & 0 & 0 \\ 0 & 5 & -5.5 & 0.5 \\ 0 & 0 & 0 & 0 \end{matrix} \right)
\overline{\boldsymbol{T}} = \left( \begin{matrix} -6 & 4 & 2 & 0 \\ 1 & -1 & 0 & 0 \\ 0 & 5 & -5.5 & 0.5 \\ 0 & 0 & 0 & 0 \end{matrix} \right)
α=(13,13,13,0)⊤\boldsymbol{\alpha} = ( \frac13, \frac13, \frac13, 0 )^\top
\boldsymbol{\alpha} = ( \frac13, \frac13, \frac13, 0 )^\top
22
2
44
4
11
1
0.50.5
0.5
55
5

What are phase-type distributions?

Markov chain                             State space

(Xt)t≥0( X_t )_{t \ge 0}
( X_t )_{t \ge 0}
{1,...,p,†}\{1, ..., p, \dagger \}
\{1, ..., p, \dagger \}

Phase-type definition

Markov chain                             State space

 

 

 

 

 

  • Initial distribution
     
  • Sub-transition matrix
     
  • Exit rates

 

α\boldsymbol{\alpha}
\boldsymbol{\alpha}
T\boldsymbol{T}
\boldsymbol{T}
t=−T1\boldsymbol{t} = -\boldsymbol{T} 1
\boldsymbol{t} = -\boldsymbol{T} 1
t\boldsymbol{t}
\boldsymbol{t}
τ=inf⁡t{Xt=†}\tau = \inf_t \{ X_t = \dagger \}
\tau = \inf_t \{ X_t = \dagger \}
(Xt)t≥0( X_t )_{t \ge 0}
( X_t )_{t \ge 0}
{1,...,p,†}\{1, ..., p, \dagger \}
\{1, ..., p, \dagger \}
⇔τ∼PhaseType(α,T)\Leftrightarrow \tau \sim \mathrm{PhaseType}(\boldsymbol{\alpha}, \boldsymbol{T})
\Leftrightarrow \tau \sim \mathrm{PhaseType}(\boldsymbol{\alpha}, \boldsymbol{T})
T‾=(Tt00)\overline{\boldsymbol{T}} = \left( \begin{matrix} \boldsymbol{T} & \boldsymbol{t} \\ 0 & 0 \end{matrix} \right)
\overline{\boldsymbol{T}} = \left( \begin{matrix} \boldsymbol{T} & \boldsymbol{t} \\ 0 & 0 \end{matrix} \right)

Phase-type properties

 

 

Matrix exponential

 

Density and tail

 

 

Moments

 

 

Laplace transform

fτ(s)=α⊤eTstf_\tau(s) = \boldsymbol{\alpha}^\top \mathrm{e}^{\boldsymbol{T} s} \boldsymbol{t}
f_\tau(s) = \boldsymbol{\alpha}^\top \mathrm{e}^{\boldsymbol{T} s} \boldsymbol{t}
eTs=∑i=0∞(Ts)ii!\mathrm{e}^{\boldsymbol{T} s} = \sum_{i=0}^\infty \frac{(\boldsymbol{T} s)^i}{i!}
\mathrm{e}^{\boldsymbol{T} s} = \sum_{i=0}^\infty \frac{(\boldsymbol{T} s)^i}{i!}
τ∼PhaseType(α,T)\tau \sim \mathrm{PhaseType}(\boldsymbol{\alpha}, \boldsymbol{T})
\tau \sim \mathrm{PhaseType}(\boldsymbol{\alpha}, \boldsymbol{T})
F‾τ(s)=α⊤eTs1\overline{F}_\tau(s) = \boldsymbol{\alpha}^\top \mathrm{e}^{\boldsymbol{T} s} 1
\overline{F}_\tau(s) = \boldsymbol{\alpha}^\top \mathrm{e}^{\boldsymbol{T} s} 1
E[τ]=−α⊤T−11\mathbb{E}[\tau] = {-}\boldsymbol{\alpha}^\top \boldsymbol{T}^{-1} \boldsymbol{1}
\mathbb{E}[\tau] = {-}\boldsymbol{\alpha}^\top \boldsymbol{T}^{-1} \boldsymbol{1}
E[τn]=(−1)nn!  α⊤T−n1\mathbb{E}[\tau^n] = (-1)^n n! \,\, \boldsymbol{\alpha}^\top \boldsymbol{T}^{-n} \boldsymbol{1}
\mathbb{E}[\tau^n] = (-1)^n n! \,\, \boldsymbol{\alpha}^\top \boldsymbol{T}^{-n} \boldsymbol{1}
E[e−sτ]=α⊤(sI−T)−1t\mathbb{E}[\mathrm{e}^{-s\tau}] = \boldsymbol{\alpha}^\top (s \boldsymbol{I} - \boldsymbol{T})^{-1} \boldsymbol{t}
\mathbb{E}[\mathrm{e}^{-s\tau}] = \boldsymbol{\alpha}^\top (s \boldsymbol{I} - \boldsymbol{T})^{-1} \boldsymbol{t}

Class of phase-types is dense

S. Asmussen (2003), Applied Probability and Queues, 2nd Edition, Springer

Phase-type generalises...

  • Exponential distribution


     
  • Sums of exponentials (Erlang distribution)




     
  • Mixtures of exponentials (hyperexponential distribution)
α=(1),T=(−λ),t=(λ)\boldsymbol{\alpha} = \left( 1 \right), \boldsymbol{T} = \left( -\lambda \right), \boldsymbol{t} = \left( \lambda \right)
\boldsymbol{\alpha} = \left( 1 \right), \boldsymbol{T} = \left( -\lambda \right), \boldsymbol{t} = \left( \lambda \right)
α=(100),T=(−λ1λ100−λ2λ200−λ3),t=(00λ3)\boldsymbol{\alpha} = \left( \begin{matrix} 1 \\ 0 \\ 0 \end{matrix} \right) , \boldsymbol{T} = \left( \begin{matrix} -\lambda_1 & \lambda_1 & 0 \\ 0 & -\lambda_2 & \lambda_2 \\ 0 & 0 & -\lambda_3 \end{matrix} \right) , \boldsymbol{t} = \left( \begin{matrix} 0 \\ 0 \\ \lambda_3 \end{matrix} \right)
\boldsymbol{\alpha} = \left( \begin{matrix} 1 \\ 0 \\ 0 \end{matrix} \right) , \boldsymbol{T} = \left( \begin{matrix} -\lambda_1 & \lambda_1 & 0 \\ 0 & -\lambda_2 & \lambda_2 \\ 0 & 0 & -\lambda_3 \end{matrix} \right) , \boldsymbol{t} = \left( \begin{matrix} 0 \\ 0 \\ \lambda_3 \end{matrix} \right)
α=(α1α2α3),T=(−λ1000−λ2000−λ3),t=(λ1λ2λ3)\boldsymbol{\alpha} = \left( \begin{matrix} \alpha_1 \\ \alpha_2 \\ \alpha_3 \end{matrix} \right) , \boldsymbol{T} = \left( \begin{matrix} -\lambda_1 & 0 & 0 \\ 0 & -\lambda_2 & 0 \\ 0 & 0 & -\lambda_3 \end{matrix} \right) , \boldsymbol{t} = \left( \begin{matrix} \lambda_1 \\ \lambda_2 \\ \lambda_3 \end{matrix} \right)
\boldsymbol{\alpha} = \left( \begin{matrix} \alpha_1 \\ \alpha_2 \\ \alpha_3 \end{matrix} \right) , \boldsymbol{T} = \left( \begin{matrix} -\lambda_1 & 0 & 0 \\ 0 & -\lambda_2 & 0 \\ 0 & 0 & -\lambda_3 \end{matrix} \right) , \boldsymbol{t} = \left( \begin{matrix} \lambda_1 \\ \lambda_2 \\ \lambda_3 \end{matrix} \right)

More cool properties

Closure under addition, minimum, maximum

(τ∣τ>s)∼PhaseType(αs,T)(\tau \mid \tau > s) \sim \mathrm{PhaseType}(\boldsymbol{\alpha}_s, \boldsymbol{T})
(\tau \mid \tau > s) \sim \mathrm{PhaseType}(\boldsymbol{\alpha}_s, \boldsymbol{T})
τi∼PhaseType(αi,Ti)\tau_i \sim \mathrm{PhaseType}(\boldsymbol{\alpha}_i, \boldsymbol{T}_i)
\tau_i \sim \mathrm{PhaseType}(\boldsymbol{\alpha}_i, \boldsymbol{T}_i)
⇒τ1+τ2∼PhaseType(…,… )\Rightarrow \tau_1 + \tau_2 \sim \mathrm{PhaseType}(\dots, \dots)
\Rightarrow \tau_1 + \tau_2 \sim \mathrm{PhaseType}(\dots, \dots)
⇒min⁡{τ1,τ2}∼PhaseType(…,… )\Rightarrow \min\{ \tau_1 , \tau_2 \} \sim \mathrm{PhaseType}(\dots, \dots)
\Rightarrow \min\{ \tau_1 , \tau_2 \} \sim \mathrm{PhaseType}(\dots, \dots)
αs⊤=F‾τ(s)−1α⊤eTs\boldsymbol{\alpha}_s^\top = \overline{F}_\tau(s)^{-1} \boldsymbol{\alpha}^\top \mathrm{e}^{\boldsymbol{T} s}
\boldsymbol{\alpha}_s^\top = \overline{F}_\tau(s)^{-1} \boldsymbol{\alpha}^\top \mathrm{e}^{\boldsymbol{T} s}

... and under conditioning

Two ways to view the phases

As meaningless mathematical artefacts

Choose number of phases to balance accuracy and over-fitting

As states which reflect some part of reality

Choose number of phases to match reality

X.S. Lin & X. Liu (2007) Markov aging process and phase-type law of mortality.
N. Amer. Act J. 11, pp. 92-109

M. Govorun, G. Latouche, & S. Loisel (2015). Phase-type aging modeling for health dependent costs. Insurance: Mathematics and Economics, 62, pp. 173-183.

If it works for exponential distribution, try phase-type

Assume:

  •        is exponentially distributed
     
  •                           where              is a Brownian motion

 

Then              and                              are independent and exponentially distributed with rates

 

τ\tau
\tau
St=eXtS_t = \mathrm{e}^{X_t}
S_t = \mathrm{e}^{X_t}
XtX_t
X_t
X‾τ\overline{X}_\tau
\overline{X}_\tau
X‾τ−Xτ\overline{X}_\tau - X_\tau
\overline{X}_\tau - X_\tau
λ±=∓μσ2+μ2σ4+2λσ2\lambda_{\pm} = \mp \frac{\mu}{\sigma^2} + \sqrt{ \frac{\mu^2}{\sigma^4} + \frac{2\lambda}{\sigma^2} }
\lambda_{\pm} = \mp \frac{\mu}{\sigma^2} + \sqrt{ \frac{\mu^2}{\sigma^4} + \frac{2\lambda}{\sigma^2} }
λ\lambda
\lambda
μ,σ2\mu, \sigma^2
\mu, \sigma^2

Wiener-Hopf Factorisation

P(X‾τ∈dx,Xτ−X‾τ∈dy)=P(X‾τ∈dx)P(X‾τ∈dy)\mathbb{P}(\overline{X}_\tau \in \mathrm{d}x, X_\tau - \overline{X}_\tau \in \mathrm{d}y) = \mathbb{P}(\overline{X}_\tau \in \mathrm{d}x) \mathbb{P}(\underline{X}_\tau \in \mathrm{d}y)
\mathbb{P}(\overline{X}_\tau \in \mathrm{d}x, X_\tau - \overline{X}_\tau \in \mathrm{d}y) = \mathbb{P}(\overline{X}_\tau \in \mathrm{d}x) \mathbb{P}(\underline{X}_\tau \in \mathrm{d}y)
XtX_t
X_t
  •        is an exponential random variable
     
  •         is a Lévy process
τ\tau
\tau

Doesn't work for non-random time

P(X‾t∈dx,Xt−X‾t∈dy∣σ‾t=s)\mathbb{P}(\overline{X}_t \in \mathrm{d}x, X_t - \overline{X}_t \in \mathrm{d}y \mid \overline{\sigma}_t = s)
\mathbb{P}(\overline{X}_t \in \mathrm{d}x, X_t - \overline{X}_t \in \mathrm{d}y \mid \overline{\sigma}_t = s)
=P(X‾t∈dx∣σ‾t=s)P(X‾t∈dy∣σ‾t=t−s)= \mathbb{P}(\overline{X}_t \in \mathrm{d}x \mid \overline{\sigma}_t = s) \mathbb{P}(\underline{X}_t \in \mathrm{d}y \mid \underline{\sigma}_t = t - s)
= \mathbb{P}(\overline{X}_t \in \mathrm{d}x \mid \overline{\sigma}_t = s) \mathbb{P}(\underline{X}_t \in \mathrm{d}y \mid \underline{\sigma}_t = t - s)

How to fit them?

Traditionally, using EM algorithm

Bladt, M., Gonzalez, A. and Lauritzen, S. L. (2003), ‘The estimation of Phase-type related functionals using Markov chain Monte Carlo methods’, Scandinavian Actuarial Journal

Representation is not unique

α=(1,0,0)⊤\boldsymbol{\alpha} = ( 1, 0, 0 )^\top
\boldsymbol{\alpha} = ( 1, 0, 0 )^\top
T1=(−1100−2200−3)\boldsymbol{T}_1 = \left( \begin{matrix} -1 & 1 & 0 \\ 0 & -2 & 2 \\ 0 & 0 & -3 \end{matrix} \right)
\boldsymbol{T}_1 = \left( \begin{matrix} -1 & 1 & 0 \\ 0 & -2 & 2 \\ 0 & 0 & -3 \end{matrix} \right)
T2=(−3300−2200−1)\boldsymbol{T}_2 = \left( \begin{matrix} -3 & 3 & 0 \\ 0 & -2 & 2 \\ 0 & 0 & -1 \end{matrix} \right)
\boldsymbol{T}_2 = \left( \begin{matrix} -3 & 3 & 0 \\ 0 & -2 & 2 \\ 0 & 0 & -1 \end{matrix} \right)
τ1∼PhaseType(α,T1)\tau_1 \sim \mathrm{PhaseType}(\boldsymbol{\alpha}, \boldsymbol{T}_1)
\tau_1 \sim \mathrm{PhaseType}(\boldsymbol{\alpha}, \boldsymbol{T}_1)
τ2∼PhaseType(α,T2)\tau_2 \sim \mathrm{PhaseType}(\boldsymbol{\alpha}, \boldsymbol{T}_2)
\tau_2 \sim \mathrm{PhaseType}(\boldsymbol{\alpha}, \boldsymbol{T}_2)
τ1=Dτ2\tau_1 \overset{\mathscr{D}}{=} \tau_2
\tau_1 \overset{\mathscr{D}}{=} \tau_2

Also, not easy to tell if any parameters produce a valid distribution

Lots of parameters to fit

  • General



     
  • Coxian distribution
α=(100),T=(−λ1λ1200−λ2λ2300−λ3)\boldsymbol{\alpha} = \left( \begin{matrix} 1 \\ 0 \\ 0 \end{matrix} \right) , \quad \boldsymbol{T} = \left( \begin{matrix} -\lambda_1 & \lambda_{12} & 0 \\ 0 & -\lambda_2 & \lambda_{23} \\ 0 & 0 & -\lambda_3 \end{matrix} \right)
\boldsymbol{\alpha} = \left( \begin{matrix} 1 \\ 0 \\ 0 \end{matrix} \right) , \quad \boldsymbol{T} = \left( \begin{matrix} -\lambda_1 & \lambda_{12} & 0 \\ 0 & -\lambda_2 & \lambda_{23} \\ 0 & 0 & -\lambda_3 \end{matrix} \right)
α=(α1α2α3),T=(−λ1λ12λ13λ21−λ2λ23λ31λ32−λ3)\boldsymbol{\alpha} = \left( \begin{matrix} \alpha_1 \\ \alpha_2 \\ \alpha_3 \end{matrix} \right) , \quad \boldsymbol{T} = \left( \begin{matrix} -\lambda_1 & \lambda_{12} & \lambda_{13} \\ \lambda_{21} & -\lambda_2 & \lambda_{23} \\ \lambda_{31} & \lambda_{32} & -\lambda_3 \end{matrix} \right)
\boldsymbol{\alpha} = \left( \begin{matrix} \alpha_1 \\ \alpha_2 \\ \alpha_3 \end{matrix} \right) , \quad \boldsymbol{T} = \left( \begin{matrix} -\lambda_1 & \lambda_{12} & \lambda_{13} \\ \lambda_{21} & -\lambda_2 & \lambda_{23} \\ \lambda_{31} & \lambda_{32} & -\lambda_3 \end{matrix} \right)
p(p+1)−1p(p+1)-1
p(p+1)-1
2p−12p-1
2p-1

Problem: to model mortality via phase-type

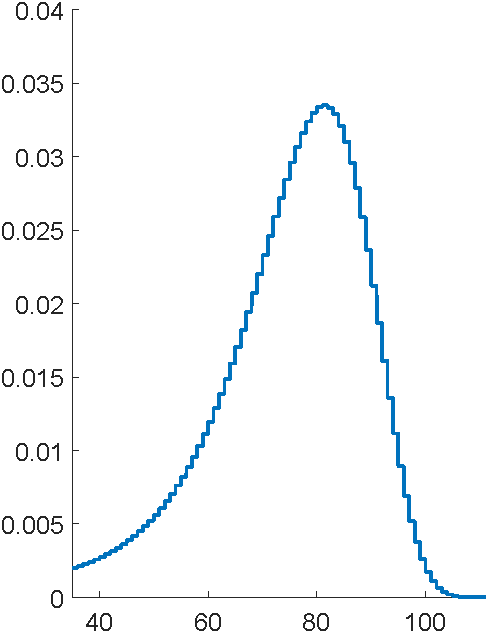
Bowers et al (1997), Actuarial Mathematics, 2nd Edition

First attempts with EMpht

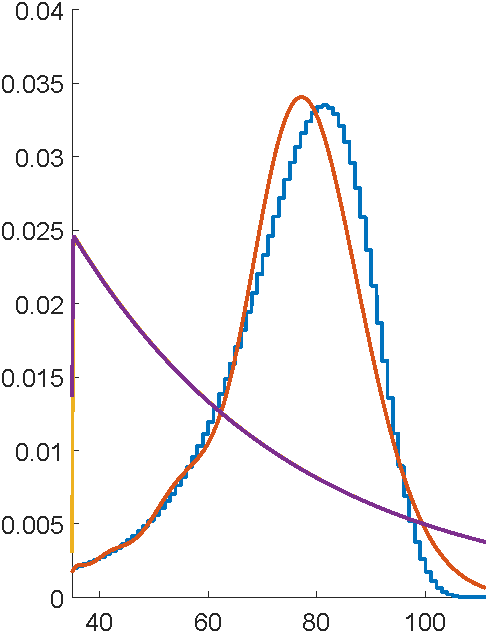
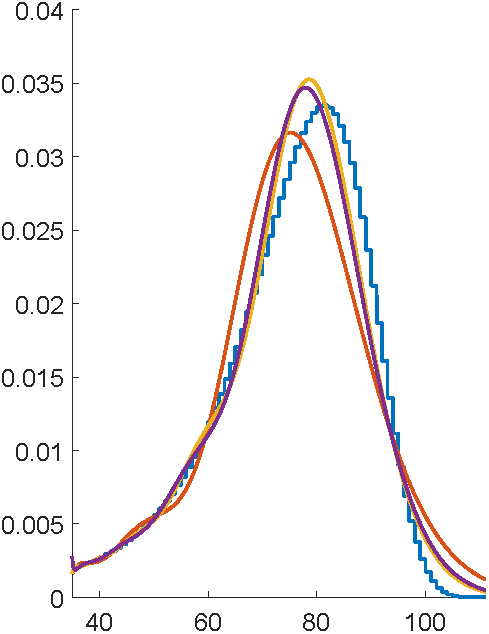
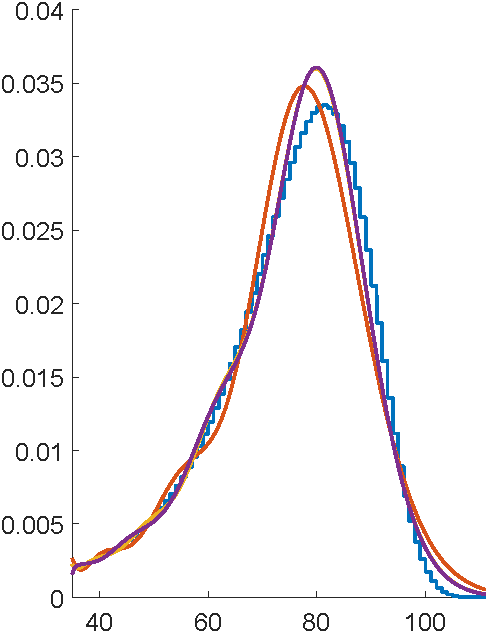
Why's this so terrible?

eTs=∑i=0∞(Ts)ii!\mathrm{e}^{\boldsymbol{T} s} = \sum_{i=0}^\infty \frac{(\boldsymbol{T} s)^i}{i!}
\mathrm{e}^{\boldsymbol{T} s} = \sum_{i=0}^\infty \frac{(\boldsymbol{T} s)^i}{i!}

"E" step has a bazillion matrix exponential calculations

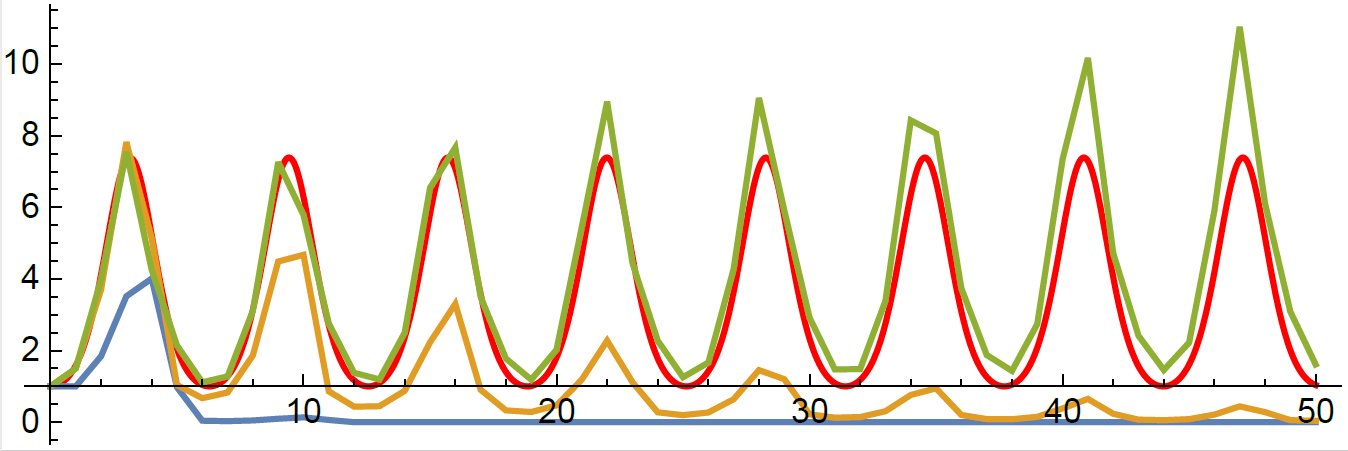
DE solver going negative

Rewrite in Julia

void rungekutta(int p, double *avector, double *gvector, double *bvector,
		double **cmatrix, double dt, double h, double **T, double *t,
		double **ka, double **kg, double **kb, double ***kc)
{
  int i, j, k, m;
  double eps, h2, sum;

  i = dt/h;
  h2 = dt/(i+1);
  init_matrix(ka, 4, p);
  init_matrix(kb, 4, p);
  init_3dimmatrix(kc, 4, p, p);
  if (kg != NULL)
    init_matrix(kg, 4, p);
    ...
    for (i=0; i < p; i++) {
      avector[i] += (ka[0][i]+2*ka[1][i]+2*ka[2][i]+ka[3][i])/6;
      bvector[i] += (kb[0][i]+2*kb[1][i]+2*kb[2][i]+kb[3][i])/6;
      for (j=0; j < p; j++)
        cmatrix[i][j] +=(kc[0][i][j]+2*kc[1][i][j]+2*kc[2][i][j]+kc[3][i][j])/6;
    }
  }
}

This function: 116 lines of C, built-in to Julia

Whole program: 1700 lines of C, 300 lines of Julia 

# Run the ODE solver.
u0 = zeros(p*p)
pf = ParameterizedFunction(ode_observations!, fit)
prob = ODEProblem(pf, u0, (0.0, maximum(s.obs)))
sol = solve(prob, OwrenZen5())

https://github.com/Pat-Laub/EMpht.jl

# Run the ODE solver.
u0 = zeros(p*p)
pf = ParameterizedFunction(ode_observations!, fit)
prob = ODEProblem(pf, u0, (0.0, maximum(s.obs)))
sol = solve(prob, OwrenZen5())

...

u = sol(s.obs[k])
C = reshape(u, p, p)
if minimum(C) < 0
    (C,err) = hquadrature(p*p, (x,v) -> c_integrand(x, v, fit, s.obs[k]), 
                0, s.obs[k], reltol=1e-1, maxevals=500)
    C = reshape(C, p, p)
end

Swap to quadrature in Julia

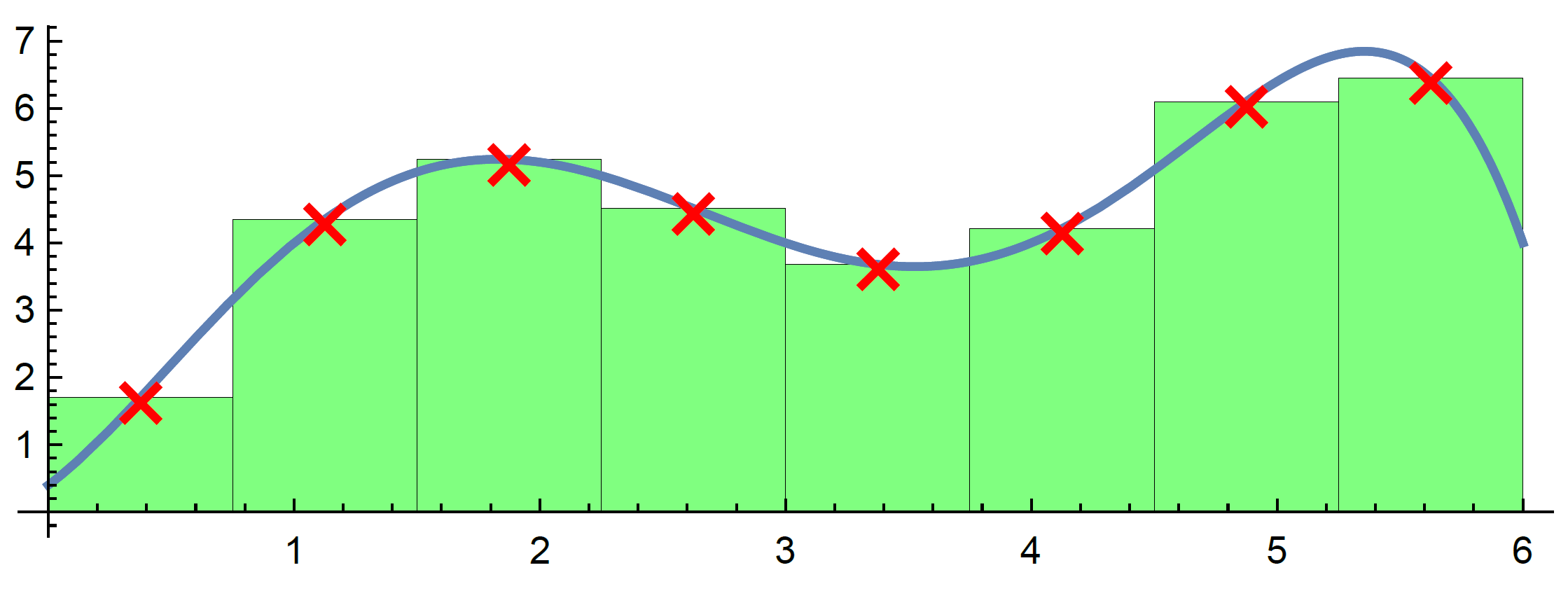
Swap to quadrature in Julia

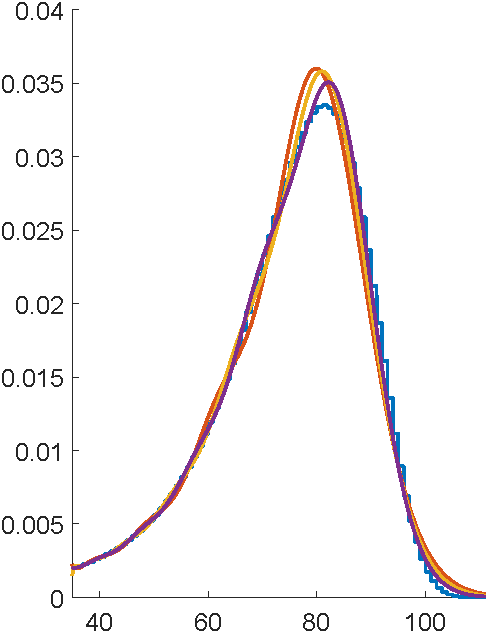
Better starting value

Canonical form 1

α=(α1α2α3),T=(−λ1λ100−λ2λ200−λ3)\boldsymbol{\alpha} = \left( \begin{matrix} \alpha_1 \\ \alpha_2 \\ \alpha_3 \end{matrix} \right) , \quad \boldsymbol{T} = \left( \begin{matrix} -\lambda_1 & \lambda_1 & 0 \\ 0 & -\lambda_2 & \lambda_2 \\ 0 & 0 & -\lambda_3 \end{matrix} \right)
\boldsymbol{\alpha} = \left( \begin{matrix} \alpha_1 \\ \alpha_2 \\ \alpha_3 \end{matrix} \right) , \quad \boldsymbol{T} = \left( \begin{matrix} -\lambda_1 & \lambda_1 & 0 \\ 0 & -\lambda_2 & \lambda_2 \\ 0 & 0 & -\lambda_3 \end{matrix} \right)
λ1<λ2<⋯<λp\lambda_1 < \lambda_2 < \dots < \lambda_p
\lambda_1 < \lambda_2 < \dots < \lambda_p

Uniformization magic

Et voilà

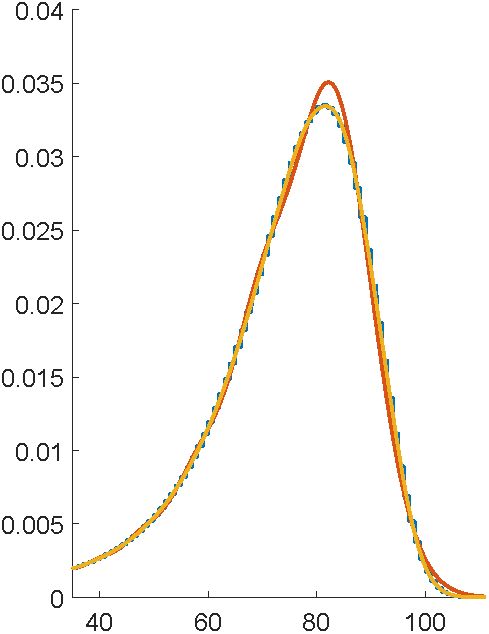
E[e−δ(τ∧T)Ψ(S‾τ∧T,Sτ∧T)]\mathbb{E}[ \mathrm{e}^{-\delta (\tau \wedge T) } \Psi(\overline{S}_{\tau \wedge T}, S_{\tau \wedge T}) ]
\mathbb{E}[ \mathrm{e}^{-\delta (\tau \wedge T) } \Psi(\overline{S}_{\tau \wedge T}, S_{\tau \wedge T}) ]

Contract over a limited horizon

Can use Erlangization so

τn≈T ,τn∼Erlang(n,n/T)\tau_n \approx T \,, \quad \tau_n \sim \mathrm{Erlang}(n, n/T)
\tau_n \approx T \,, \quad \tau_n \sim \mathrm{Erlang}(n, n/T)
τ∧τn=τn∗∼PhaseType(…,… )\tau \wedge \tau_n = \tau_n^* \sim \mathrm{PhaseType}(\dots, \dots)
\tau \wedge \tau_n = \tau_n^* \sim \mathrm{PhaseType}(\dots, \dots)
…≈E[e−δτn∗Ψ(S‾τn∗,Sτn∗)]\ldots \approx \mathbb{E}[ \mathrm{e}^{-\delta \tau_n^* } \Psi(\overline{S}_{\tau_n^*}, S_{\tau_n^*}) ]
\ldots \approx \mathbb{E}[ \mathrm{e}^{-\delta \tau_n^* } \Psi(\overline{S}_{\tau_n^*}, S_{\tau_n^*}) ]

and phase-type closure under minimums

Payout occurs at death or after fixed duration T, whichever first

Thanks for listening!

https://people.smp.uq.edu.au/YoniNazarathy/julia-stats/StatisticsWithJulia.pdf

https://github.com/Pat-Laub/EMPHt.jl

Phase-type distributions

Markov chain                             State space

 

 

 

 

(Xt)t≥0( X_t )_{t \ge 0}
( X_t )_{t \ge 0}
{1,...,p,†}\{1, ..., p, \dagger \}
\{1, ..., p, \dagger \}
Made with Slides.com