Phase-Type Models in
Life Insurance

Dr Patrick J. Laub

Université Lyon 1

Work

Coffee

Lunch

Home

Chat

A typical work day

Work

Coffee

Lunch

Home

Bisous

Pause Café

Paperwork

Déjeuner

Il y a un pot

Une petite pinte

Paperwork

Sieste

(Talk)

A typical French work day

Work

Coffee

Lunch

Home

Chat

1/3

1

\boldsymbol{P} = \begin{bmatrix} 0 & 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & \frac13 & 0 & \frac13 & \frac13 \\ 0 & 0 & 0 & 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & 0 & 0 & 0 & 1 \\ \end{bmatrix}

2

5

1

4

3

7

6

1/3

1

\boldsymbol{\alpha} = \begin{bmatrix} 0.99 \\ 0.01 \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ \end{bmatrix}

\begin{matrix} 1 & 2 & 3 & 4 & 5 & 6 & 7 \\ \end{matrix}

\begin{matrix} 1 \\ 2 \\ 3 \\ 4 \\ 5 \\ 6 \\ 7 \end{matrix}

From Markov chains to Markov processes

Coffee
Work
Lunch
Coffee
Work
Chat
Work
Home

State	Time in State
Coffee	5 mins
Work	2 hours 3 mins
Lunch	26 mins
Coffee	11 mins
Work	1 hour 37 mins
Chat	45 mins
Work	2 hours 1 mins

Chain

Discrete Time

Process

Continuous Time

t

X_t

Example Markov process

( X_t )_{t \ge 0}

The Markov property

Markov chain State space

\{ X_n \}_{n \ge 0}

\{1, ..., p \}

\mathbb{P}(X_{n+1} = i \mid X_0 = x_0, \dots, X_n = x_n) = \mathbb{P}(X_n = i \mid X_n = x_n)

Markov process at times

( X_t )_{t \ge 0}

\mathbb{P}(X_{t_{n+1}} = i \mid X_{t_0} = x_{t_0}, \dots, X_{t_n} = x_{t_n}) = \mathbb{P}(X_{t_{n+1}} = i \mid X_{t_n} = x_{t_n})

0 \le t_1 < \dots < t_n < t_{n+1}

Sojourn times

Sojourn times are the random lengths of time spent in each state

S_1

S_2

S_3

S_5^{(1)}

S_5^{(2)}

S_1 \sim \mathsf{Exp}(1/\mu_1)

S_2 \sim \mathsf{Exp}(1/\mu_2)

S_5^{(1)}, S_5^{(2)} \overset{\mathrm{i.i.d.}}{\sim} \mathsf{Exp}(1/\mu_5)

S_4

\mathbb{P}(E > t+s \mid E > t) = \mathbb{P}(E > s)

Transition rate matrices

\boldsymbol{P} = \begin{bmatrix} 0 & 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & \frac13 & 0 & \frac13 & \frac13 \\ 0 & 0 & 0 & 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & 0 & 0 & 0 & 1 \\ \end{bmatrix}

2

5

1

4

3

7

6

1/3

1

\boldsymbol{Q} = \begin{bmatrix} -10 & 10 & 0 & 0 & 0 & 0 & 0 \\ 0 & -\frac23 & \frac23 & 0 & 0 & 0 & 0 \\ 0 & 0 & -2 & 2 & 0 & 0 & 0 \\ 0 & 0 & 0 & -10 & 10 & 0 & 0 \\ 0 & 0 & 0 & \frac23 & -2 & \frac23 & \frac23 \\ 0 & 0 & 0 & 0 & \frac43 & -\frac43 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 \end{bmatrix}

S_i \sim \mathsf{Exp}(\lambda_i = 1/\mu_i)

\begin{aligned} \mu_1 = 0.1 &\Leftrightarrow \lambda_1 = 10 \\ \mu_2 = 1.5 &\Leftrightarrow \lambda_2 = \frac23 \\ \mu_3 = 0.5 &\Leftrightarrow \lambda_3 = 2 \\ \mu_4 = 0.1 &\Leftrightarrow \lambda_3 = 10 \\ \mu_5 = 0.5 &\Leftrightarrow \lambda_5 = 2 \\ \mu_6 = 0.75 &\Leftrightarrow \lambda_6 = \frac43 \\ \mu_6 = \infty &\Leftrightarrow \lambda_6 = 0 \end{aligned}

\boldsymbol{\alpha} = [ 0.99, 0.01, 0, 0, \dots ]^\top

\begin{matrix} 1 & 2 & 3 & 4 & 5 & 6 & 7 \\ \end{matrix}

\begin{matrix} 1 \\ 2 \\ 3 \\ 4 \\ 5 \\ 6 \\ 7 \end{matrix}

\begin{matrix} 1~~ & 2~~ & 3~~ & 4~~ & 5~~ & 6~~ & 7 \\ \end{matrix}

\begin{matrix} 1 \\ 2 \\ 3 \\ 4 \\ 5 \\ 6 \\ 7 \end{matrix}

Phase-type definition

Markov process State space

Initial distribution
Sub-transition matrix
Exit rates

\boldsymbol{\alpha}

\boldsymbol{T}

\boldsymbol{t} = -\boldsymbol{T} 1

\boldsymbol{t}

\tau = \inf_t \{ X_t = \dagger \}

( X_t )_{t \ge 0}

\{1, ..., p, \dagger \}

\Leftrightarrow \tau \sim \mathrm{PhaseType}(\boldsymbol{\alpha}, \boldsymbol{T})

\boldsymbol{Q} = \begin{bmatrix} \boldsymbol{T} & \boldsymbol{t} \\ 0 & 0 \end{bmatrix}

\dagger

1

3

2

\boldsymbol{Q} = \begin{bmatrix} -6 & 4 & 2 & 0 \\ 1 & -1 & 0 & 0 \\ 0 & 5 & -5.5 & 0.5 \\ 0 & 0 & 0 & 0 \end{bmatrix}

\boldsymbol{\alpha} = [ \frac13, \frac13, \frac13, 0 ]^\top

2

4

1

0.5

5

Example

Markov process State space

( X_t )_{t \ge 0}

\{1, 2, 3, \dagger \}

\boldsymbol{T} = \begin{bmatrix} -6 & 4 & 2 \\ 1 & -1 & 0 \\ 0 & 5 & -5.5 \end{bmatrix}

\boldsymbol{t} = \begin{bmatrix} 0 \\ 0 \\ 0.5 \end{bmatrix}

Phase-type distributions

Markov chain State space

( X_t )_{t \ge 0}

\{1, ..., p, \dagger = 0\}

Phase-type quiz...

\boldsymbol{\alpha} = [ 1 ], \boldsymbol{T} = [ -2 ], \boldsymbol{t} = [ 2 ]

\boldsymbol{\alpha} = \begin{bmatrix} 1 \\ 0 \end{bmatrix} , \boldsymbol{T} = \begin{bmatrix} -1 & 1 \\ 0 & -2 \\ \end{bmatrix} , \boldsymbol{t} = \begin{bmatrix} 0 \\ 2 \end{bmatrix}

\boldsymbol{\alpha} = \begin{bmatrix} 0.5 \\ 0.5 \end{bmatrix} , \boldsymbol{T} = \begin{bmatrix} -1 & 0 \\ 0 & -2 \end{bmatrix} , \boldsymbol{t} = \begin{bmatrix} 1 \\ 2 \end{bmatrix}

Phase-type generalises...

Exponential distribution
Sums of exponentials (Erlang distribution)
Mixtures of exponentials (hyperexponential distribution)

\boldsymbol{\alpha} = [ 1 ], \boldsymbol{T} = [ -\lambda ], \boldsymbol{t} = [ \lambda ]

\boldsymbol{\alpha} = \begin{bmatrix} 1 \\ 0 \\ 0 \end{bmatrix} , \boldsymbol{T} = \begin{bmatrix} -\lambda_1 & \lambda_1 & 0 \\ 0 & -\lambda_2 & \lambda_2 \\ 0 & 0 & -\lambda_3 \end{bmatrix} , \boldsymbol{t} = \begin{bmatrix} 0 \\ 0 \\ \lambda_3 \end{bmatrix}

\boldsymbol{\alpha} = \begin{bmatrix} \alpha_1 \\ \alpha_2 \\ \alpha_3 \end{bmatrix} , \boldsymbol{T} = \begin{bmatrix} -\lambda_1 & 0 & 0 \\ 0 & -\lambda_2 & 0 \\ 0 & 0 & -\lambda_3 \end{bmatrix} , \boldsymbol{t} = \begin{bmatrix} \lambda_1 \\ \lambda_2 \\ \lambda_3 \end{bmatrix}

When to use phase-type?

When your problem has "flow chart" Markov structure.

\boldsymbol{\alpha} = \begin{bmatrix} 1 \\ 0 \\ 0 \\ \vdots \end{bmatrix} , \quad \boldsymbol{T} = \begin{bmatrix} -t_{11} & t_{12} & 0 & \\ 0 & -t_{22} & t_{23} & \dots\\ 0 & 0 & -t_{33} & \\ & \vdots & & \ddots \end{bmatrix} , \quad \boldsymbol{t} = \begin{bmatrix} t_1 \\ t_2 \\ t_3 \\ \vdots \end{bmatrix}

E.g. mortality. Age is a deterministic process, but imagine that the human body goes from physical age \(0, 1, 2, \dots\) at random speed.

("Coxian distribution")

Class of phase-types is dense

S. Asmussen (2003), Applied Probability and Queues, 2nd Edition, Springer

Class of phase-types is dense

p = 1

\text{Target}

p = 10

p = 25

p = 50

p = 100

p = 150

p = 200

p = 250

p = 300

Why does that work?

\tau_n \sim \mathrm{Erlang}(n, n/T) \,, \quad \tau_n \approx T

Can make a phase-type look like a constant value

More cool properties

Closure under addition, minimum, maximum

(\tau \mid \tau > s) \sim \mathrm{PhaseType}(\boldsymbol{\alpha}_s, \boldsymbol{T})

\tau_i \overset{\mathrm{ind.}}{\sim} \mathrm{PhaseType}(\boldsymbol{\alpha}_i, \boldsymbol{T}_i)

\Rightarrow \tau_1 + \tau_2 \sim \mathrm{PhaseType}(\dots, \dots)

\Rightarrow \min\{ \tau_1 , \tau_2 \} \sim \mathrm{PhaseType}(\dots, \dots)

... and under conditioning

\Rightarrow \max\{ \tau_1 , \tau_2 \} \sim \mathrm{PhaseType}(\dots, \dots)

Phase-type properties

Matrix exponential

Density and tail

Moments

Laplace transform

f_\tau(s) = \boldsymbol{\alpha}^\top \mathrm{e}^{\boldsymbol{T} s} \boldsymbol{t}

\mathrm{e}^{\boldsymbol{T} s} = \sum_{i=0}^\infty \frac{(\boldsymbol{T} s)^i}{i!}

\tau \sim \mathrm{PhaseType}(\boldsymbol{\alpha}, \boldsymbol{T})

\overline{F}_\tau(s) = \boldsymbol{\alpha}^\top \mathrm{e}^{\boldsymbol{T} s} 1

\mathbb{E}[\tau] = {-}\boldsymbol{\alpha}^\top \boldsymbol{T}^{-1} \boldsymbol{1}

\mathbb{E}[\tau^n] = (-1)^n n! \,\, \boldsymbol{\alpha}^\top \boldsymbol{T}^{-n} \boldsymbol{1}

\mathbb{E}[\mathrm{e}^{-s\tau}] = \boldsymbol{\alpha}^\top (s \boldsymbol{I} - \boldsymbol{T})^{-1} \boldsymbol{t}

\tau

S_t

t

Guaranteed Minimum Death Benefit

S_\tau

\text{Payoff} = \max( S_{\tau}, K )

Application

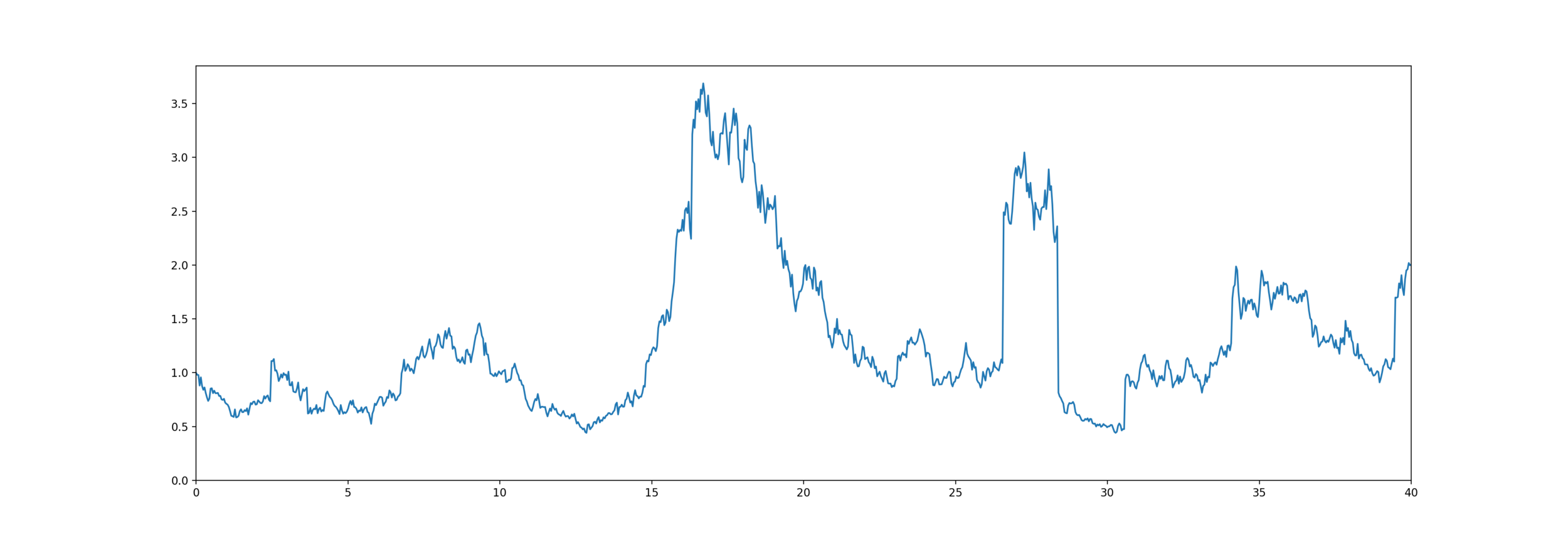
Equity-linked life insurance

\tau \sim \text{PhaseType}(\boldsymbol{\alpha}, \boldsymbol{T})

\tau

t

High Water Death Benefit

\text{Payoff} = \overline{S}_{\tau}

Equity-linked life insurance

\overline{S}_\tau

\overline{S}_t = \max_{s \le t} S_s

\tau \sim \text{PhaseType}(\boldsymbol{\alpha}, \boldsymbol{T})

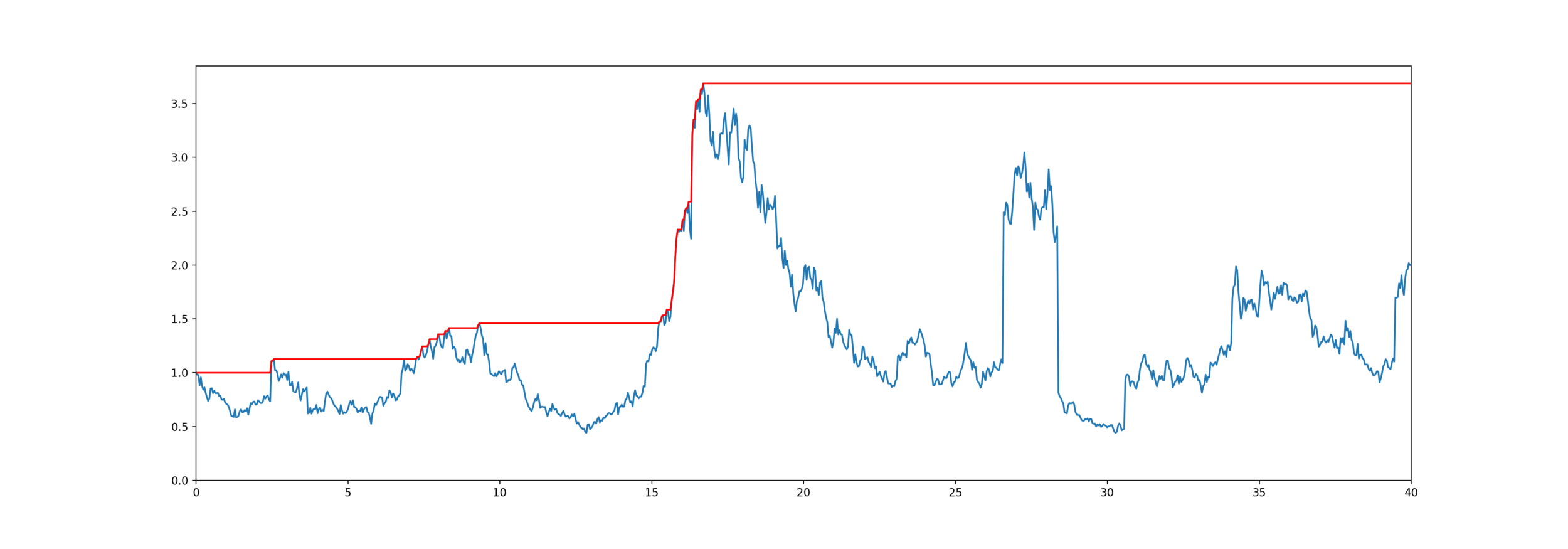
Model for mortality and equity

The customer lives for years,

\tau

\tau \sim \text{PhaseType}(\boldsymbol{\alpha}, \boldsymbol{T})

X_t \sim \text{Jump Diffusion}

S_t = S_0 \mathrm{e}^{X_t}

Equity is an exponential jump diffusion,

\text{Brownian Motion}(\mu, \sigma^2) + \text{Compound Poisson}(\lambda_1) + \text{Compound Poisson}(\lambda_2)

\text{Price} = \mathbb{E}[ \mathrm{e}^{-\delta \tau} \text{Payoff}( S_\tau, \overline{S}_\tau ) ]

S_t

t

Exponential PH-Jump Diffusion

\text{UpJumpSize}_i \overset{\mathrm{i.i.d.}}{\sim} \text{PhaseType}(\boldsymbol{\alpha}_1, \boldsymbol{T}_1)

\text{DownJumpSize}_i \overset{\mathrm{i.i.d.}}{\sim} \text{PhaseType}(\boldsymbol{\alpha}_2, \boldsymbol{T}_2)

\# \text{UpJumps}(0, t) \sim \mathrm{Poisson}(\lambda_1 t)

\# \text{DownJumps}(0, t) \sim \mathrm{Poisson}(\lambda_2 t)

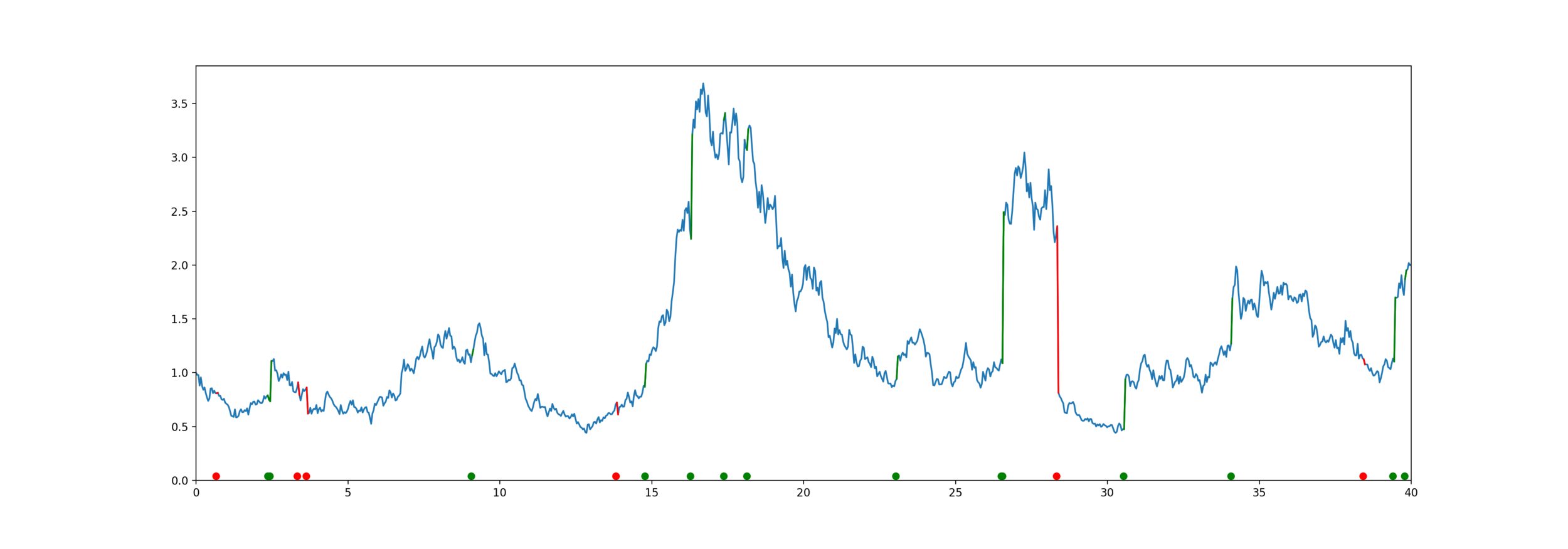
Problem: to model mortality via phase-type

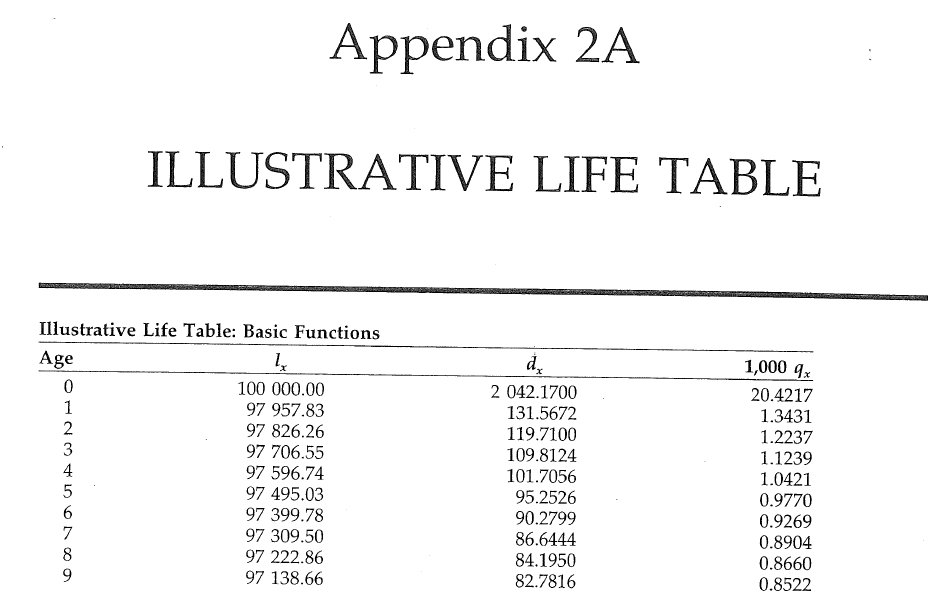
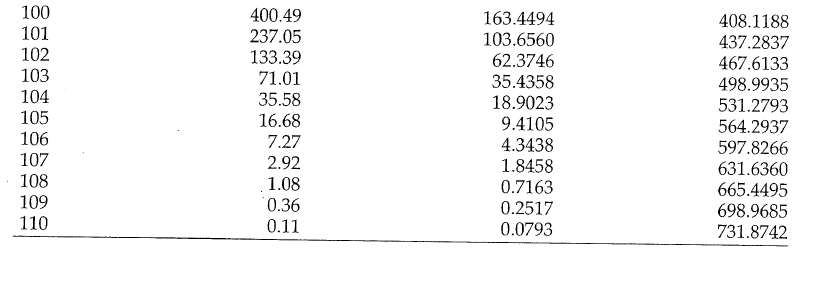
Bowers et al (1997), Actuarial Mathematics, 2nd Edition

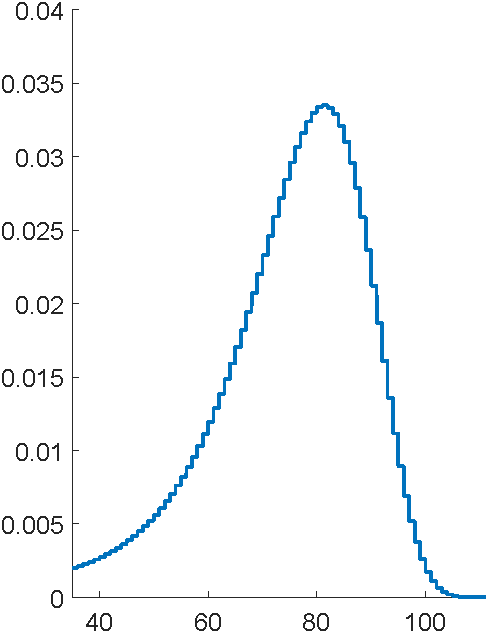
Fit General Phase-type

p = 5

p = 10

p = 20

\text{Life Table}

Representation is not unique

\boldsymbol{\alpha} = [ 1, 0, 0 ]^\top

\boldsymbol{T}_1 = \begin{bmatrix} -1 & 1 & 0 \\ 0 & -2 & 2 \\ 0 & 0 & -3 \end{bmatrix}

\boldsymbol{T}_2 = \begin{bmatrix} -3 & 3 & 0 \\ 0 & -2 & 2 \\ 0 & 0 & -1 \end{bmatrix}

\tau_1 \sim \mathrm{PhaseType}(\boldsymbol{\alpha}, \boldsymbol{T}_1)

\tau_2 \sim \mathrm{PhaseType}(\boldsymbol{\alpha}, \boldsymbol{T}_2)

\tau_1 \overset{\mathscr{D}}{=} \tau_2

Also, not easy to tell if any parameters produce a valid distribution

Lots of parameters to fit

General
Coxian distribution

\boldsymbol{\alpha} = \begin{bmatrix} 1 \\ 0 \\ 0 \end{bmatrix} , \quad \boldsymbol{T} = \begin{bmatrix} -t_{11} & t_{12} & 0 \\ 0 & -t_{22} & t_{23} \\ 0 & 0 & -t_{33} \end{bmatrix} , \quad \boldsymbol{t} = \begin{bmatrix} t_1 \\ t_2 \\ t_{33} \end{bmatrix}

\boldsymbol{\alpha} = \begin{bmatrix} \alpha_1 \\ \alpha_2 \\ \alpha_3 \end{bmatrix} , \quad \boldsymbol{T} = \begin{bmatrix} -t_{11} & t_{12} & t_{13} \\ t_{21} & -t_{22} & t_{23} \\ t_{31} & t_{32} & -t_{33} \end{bmatrix} , \quad \boldsymbol{t} = \begin{bmatrix} t_1 \\ t_2 \\ t_3 \end{bmatrix}

p^2 + (p-1)

p + (p-1)

Fit Coxian distributions

p = 5

p = 10

p = 20

\text{Life Table}

General vs Coxian

Rewrite in Julia

void rungekutta(int p, double *avector, double *gvector, double *bvector,
		double **cmatrix, double dt, double h, double **T, double *t,
		double **ka, double **kg, double **kb, double ***kc)
{
  int i, j, k, m;
  double eps, h2, sum;

  i = dt/h;
  h2 = dt/(i+1);
  init_matrix(ka, 4, p);
  init_matrix(kb, 4, p);
  init_3dimmatrix(kc, 4, p, p);
  if (kg != NULL)
    init_matrix(kg, 4, p);
    ...
    for (i=0; i < p; i++) {
      avector[i] += (ka[0][i]+2*ka[1][i]+2*ka[2][i]+ka[3][i])/6;
      bvector[i] += (kb[0][i]+2*kb[1][i]+2*kb[2][i]+kb[3][i])/6;
      for (j=0; j < p; j++)
        cmatrix[i][j] +=(kc[0][i][j]+2*kc[1][i][j]+2*kc[2][i][j]+kc[3][i][j])/6;
    }
  }
}

This function: 116 lines of C, built-in to Julia

Whole program: 1700 lines of C, 300 lines of Julia

# Run the ODE solver.
u0 = zeros(p*p)
pf = ParameterizedFunction(ode_observations!, fit)
prob = ODEProblem(pf, u0, (0.0, maximum(s.obs)))
sol = solve(prob, OwrenZen5())

https://github.com/Pat-Laub/EMpht.jl

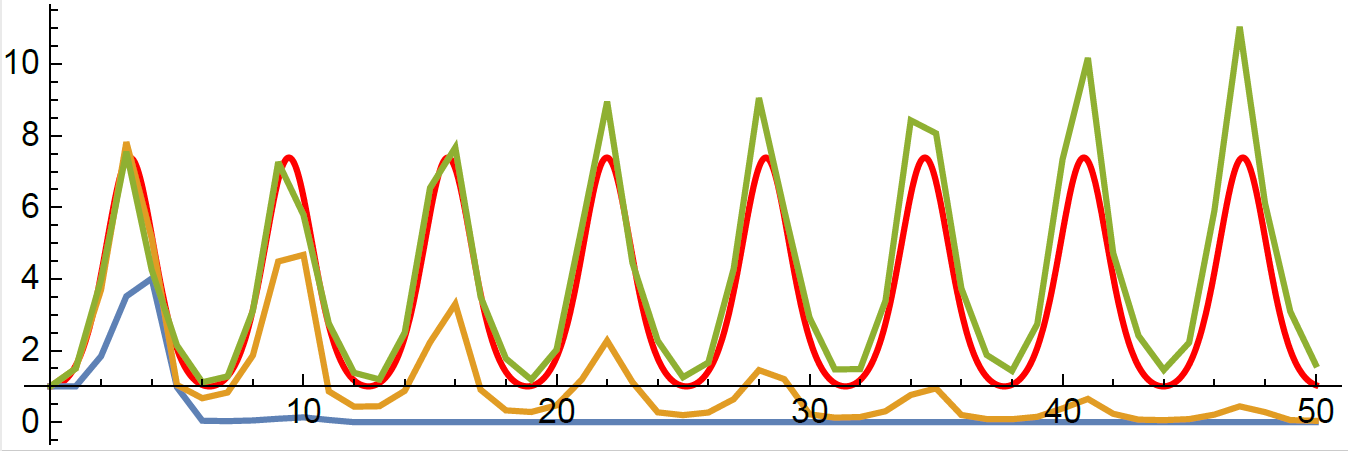
DE solver going negative

Coxian with uniformization

p = 50

p = 75

p = 100

\text{Life Table}

A twist on the Coxian form

Canonical form 1

t_{11} < t_{22} < \dots < t_{pp}

\boldsymbol{\alpha} = \begin{bmatrix} \alpha_1 \\ \alpha_2 \\ \alpha_3 \end{bmatrix} , \quad \boldsymbol{T} = \begin{bmatrix} -t_{11} & t_{11} & 0 \\ 0 & -t_{22} & t_{22} \\ 0 & 0 & -t_{33} \end{bmatrix} , \quad \boldsymbol{t} = \begin{bmatrix} 0 \\ 0 \\ t_{33} \end{bmatrix}

Et voilà

p = 200

\text{Life Table}

using Pkg; Pkg.add("EMpht")

using EMpht
lt = EMpht.parse_settings("life_table.json")[1]

phCF200 = empht(lt, p=200, ph_structure="CanonicalForm1")

f(s) = \boldsymbol{\alpha}^\top \mathrm{e}^{\boldsymbol{T} s} \boldsymbol{t}

How to fit them?

\mathrm{e}^{\boldsymbol{T} s} = \sum_{i=0}^\infty \frac{(\boldsymbol{T} s)^i}{i!}

\boldsymbol{\tau} = [\tau_1, \tau_2, \dots, \tau_n]

Observations:

L( \boldsymbol{\alpha} , \boldsymbol{T} \mid \boldsymbol{\tau} ) = \prod_{i=1}^n \boldsymbol{\alpha}^\top \mathrm{e}^{\boldsymbol{T} \tau_i} \boldsymbol{t}

\boldsymbol{t} = -\boldsymbol{T} 1

Derivatives??

\ell( \boldsymbol{\alpha} , \boldsymbol{T} \mid \boldsymbol{\tau} ) = \sum_{i=1}^n \log\Bigl\{ \boldsymbol{\alpha}^\top \left[ \sum_{j=0}^\infty \frac{(\boldsymbol{T} \tau_i)^j}{j!} \right] \boldsymbol{t} \Bigr\}

How to fit them?

\begin{aligned} L( \boldsymbol{\alpha} , \boldsymbol{T} \mid \boldsymbol{B}, \boldsymbol{Z}, \boldsymbol{N} ) &= \prod_{i=1}^p \alpha_i^{B_i} \prod_{i=1}^p \mathrm{e}^{-t_{ii} Z_i } \prod_{i,j \text{ combs}} t_{ij}^{N_{ij}} \\ \end{aligned}

Hidden values:

\(B_i\) number of MC's starting in state \(i\)

\(Z_i\) total time spend in state \(i\)

\(N_{ij}\) number of transitions from state \(i\) to \(j\)

\boldsymbol{T} = \begin{bmatrix} -t_{11} & t_{12} & t_{13} \\ t_{21} & -t_{22} & t_{23} \\ t_{31} & t_{32} & -t_{33} \end{bmatrix}

\widehat{\alpha}_i = \frac{B_i}{n}

\widehat{t}_{i} = \frac{N_{i\dagger}}{Z_i}

\boldsymbol{t} = \begin{bmatrix} t_1 \\ t_2 \\ t_3 \end{bmatrix}

\boldsymbol{\alpha} = \begin{bmatrix} \alpha_1 \\ \alpha_2 \\ \alpha_3 \end{bmatrix}

\widehat{t}_{ij} = \frac{N_{ij}}{Z_i}

\widehat{t}_{ii} = -\sum_{j\not=i} \widehat{t}_{ij}

Fitting with hidden data

EM algorithm

\boldsymbol{\tau} = [\tau_1, \tau_2, \dots, \tau_n]

Latent values:

\(B_i\) number of MC's starting in state \(i\)

\(Z_i\) total time spend in state \(i\)

\(N_{ij}\) number of transitions from state \(i\) to \(j\)

Guess \( (\boldsymbol{\alpha}^{(0)}, \boldsymbol{T}^{(0)} )\)
Iterate \(t = 0,\dots\)
1. E-step
2. M-step

\widehat{\alpha}_i^{(t+1)} = \frac{\mathbb{E}[B_i]}{n}

\widehat{t}_{ij}^{{t+1}} = \frac{\mathbb{E}[N_{ij}]}{\mathbb{E}[Z_i]}

EM algorithm:

\mathbb{E}_{(\boldsymbol{\alpha}^{(t)}, \boldsymbol{T}^{(t)})}[B_i \mid \boldsymbol{\tau}]

\mathbb{E}_{(\boldsymbol{\alpha}^{(t)}, \boldsymbol{T}^{(t)})}[Z_i \mid \boldsymbol{\tau}]

\mathbb{E}_{(\boldsymbol{\alpha}^{(t)}, \boldsymbol{T}^{(t)})}[N_{ij} \mid \boldsymbol{\tau}]

Phase-Type Models in Life Insurance

A typical work day

A typical French work day

From Markov chains to Markov processes

Example Markov process

The Markov property

Sojourn times

Transition rate matrices

Phase-type definition

Example

Phase-type distributions

Phase-type quiz...

Phase-type generalises...

When to use phase-type?

Class of phase-types is dense

Class of phase-types is dense

Why does that work?

More cool properties

Phase-type properties

Application

Equity-linked life insurance

Model for mortality and equity

Exponential PH-Jump Diffusion

Problem: to model mortality via phase-type

Fit General Phase-type

Representation is not unique

Lots of parameters to fit

Fit Coxian distributions

General vs Coxian

Rewrite in Julia

DE solver going negative

Coxian with uniformization

A twist on the Coxian form

Et voilà

How to fit them?

How to fit them?

Fitting with hidden data

EM algorithm

Phase-Type Models in
Life Insurance