Phase-Type  Models in
Life Insurance

Dr Patrick J. Laub

Who am I?

  • Software Engineering and Mathematics
     
  • PhD between University of Queensland (Brisbane) and Aarhus University
     
  • PhD supervisors:
    • Søren Asmussen
    • Phil Pollett

C'est moi!

  • Computational methods for sums of random variables

Mackay

Brisbane (University of Queensland)

Software experience

  • Assembly
  • Bash
  • C
  • C#
  • C++
  • CSS
  • Dart
  • HTML
  • Java
  • JavaScript
  • Jekyll (Markdown)
  • Julia
  • LaTeX
  • Mathematica
  • Matlab
  • Perl
  • PHP
  • Python
  • R
  • Ruby (on Rails)
  • SQL
  • Visual Basic

Sydney

Masters: Hawkes Processes

Paper version of my thesis on https://arxiv.org/abs/1507.02822

Monte Carlo

\pi \approx \, ?

Cross-entropy example

\mathbb{P}(Z > 5) \approx ? \qquad Z \sim \mathcal{N}(0,1)

Cross-entropy example

\mathbb{P}(\frac{1}{10} \int_0^{10} B(\mathrm{d} t) \ge 10) \approx \, ?

PhD outline

2015 Aarhus
2016 Jan-Jul Brisbane
2016 Aug-Dec Aarhus
2017 Brisbane/Melbourne
2018 Jan-Apr (end) China

   Supervisors: Søren Asmussen, Phil Pollett, and Jens L. Jensen

Laplace transform approximation for sums of dependent lognormals

\mathscr{L}_X(t) = \overline{\mathscr{L}}_X(t) (1 + \mathcal{O}(\frac{1}{\log(t)}))

No closed-form exists for a single lognormal

Asmussen, S., Jensen, J. L., & Rojas-Nandayapa, L. (2016). On the Laplace transform of the lognormal distribution. Methodology and Computing in Applied Probability

Orthogonal polynomial expansions

  1. Choose a reference distribution, e.g,
\nu = \mathsf{Gamma}(r,m) \Rightarrow f_\nu(x) \propto x^{r-1}\mathrm{e}^{-\frac{x}{m}}

2. Find its orthogonal polynomial system

\{ Q_n(x) \}_{n\in \mathbb{N}_0}
f_X(x) = f_\nu(x) \times \sum_{k=0}^\infty q_k Q_k(x)

3. Construct the polynomial expansion

Pierre-Olivier Goffard

Asmussen, S., Goffard, P. O., & Laub, P. J. (2017). Orthonormal polynomial expansions and lognormal sum densities. Risk and Stochastics - Festschrift for Ragnar Norberg (to appear).

My Thesis

Søren visits Melbourne

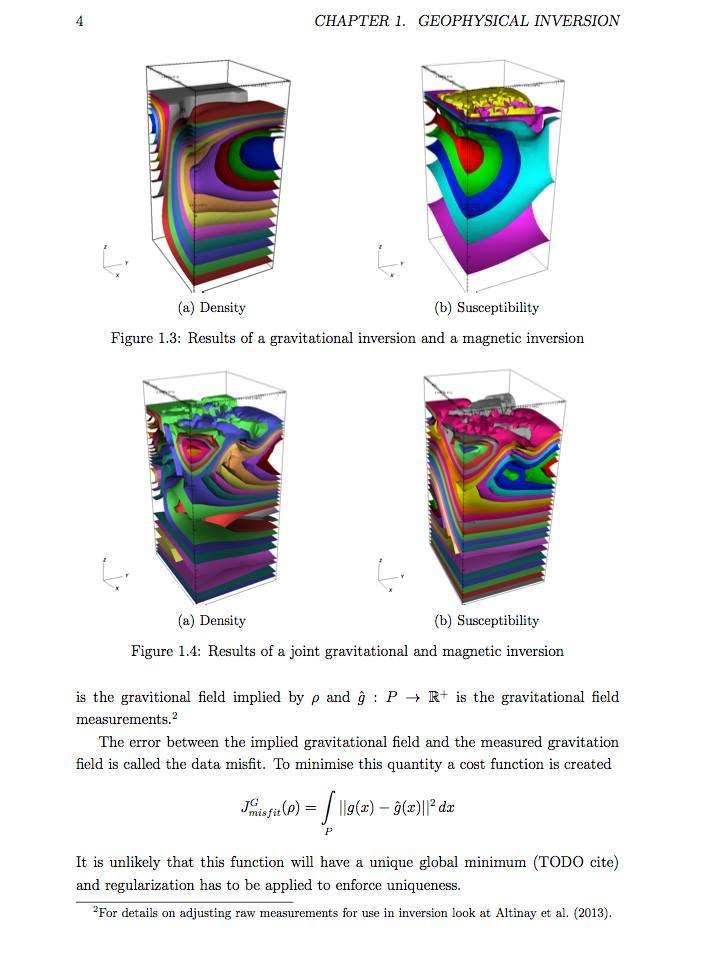
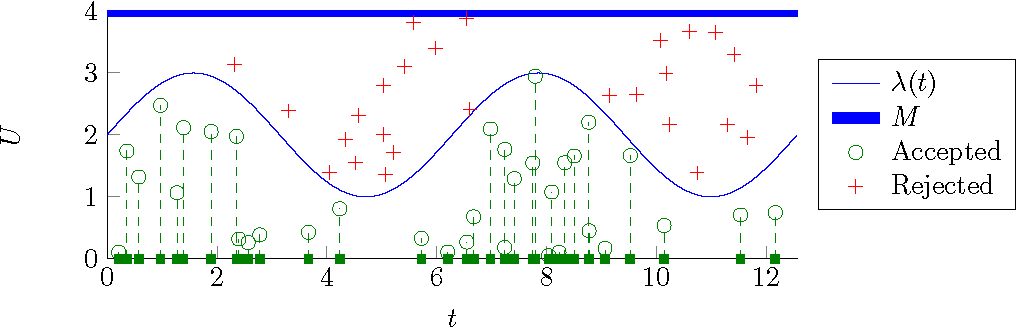
Problem: to model mortality via phase-type

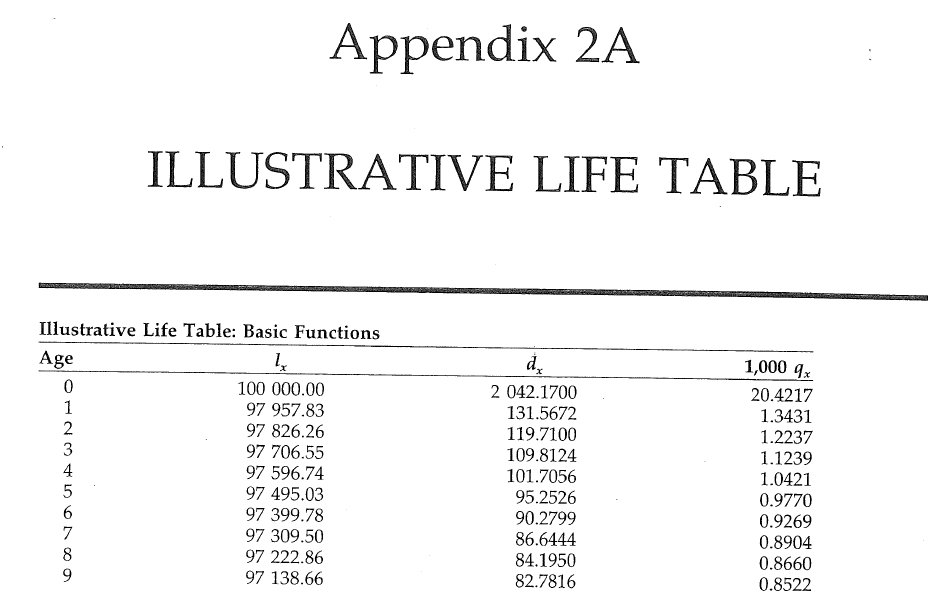
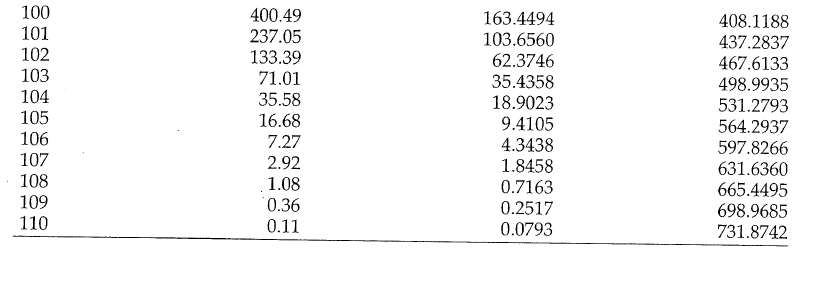
Bowers et al (1997), Actuarial Mathematics, 2nd Edition

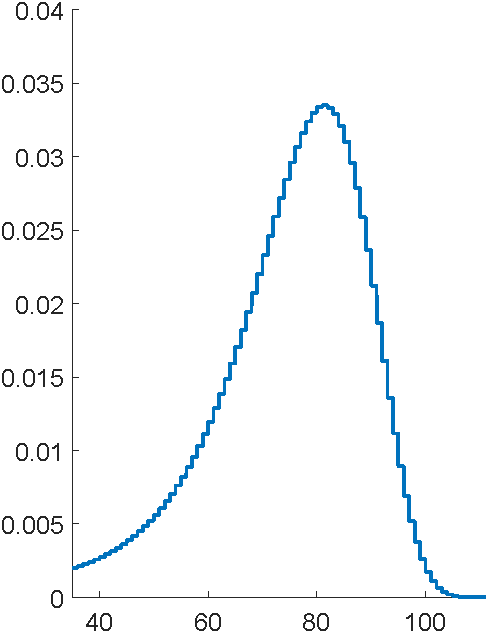
... using the C code EMpht

\dagger
1
3
2
\overline{T} = \left( \begin{matrix} -6 & 4 & 2 & 0 \\ 1 & -1 & 0 & 0 \\ 0 & 5 & -5.5 & 0.5 \\ 0 & 0 & 0 & 0 \end{matrix} \right)
\alpha = ( \frac13, \frac13, \frac13, 0 )^\top
2
4
1
0.5
5

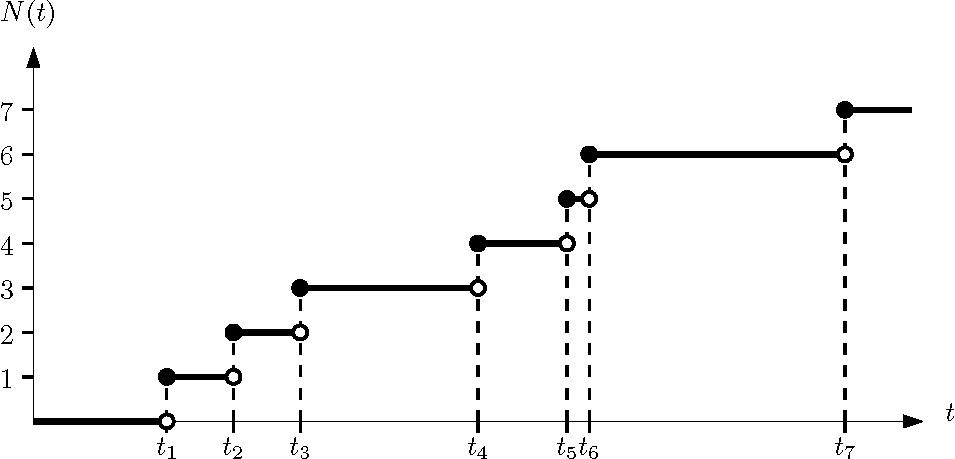
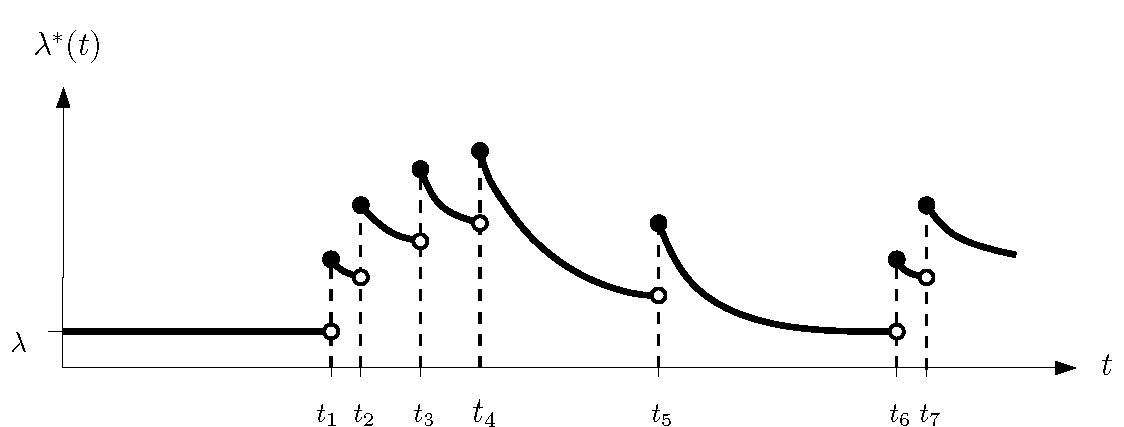
What are phase-type distributions?

Markov chain                             State space

( X_t )_{t \ge 0}
\{1, ..., p, \dagger \}

Phase-type distributions

Markov chain                             State space

 

 

 

 

( X_t )_{t \ge 0}
\{1, ..., p, \dagger \}

Phase-type definition

Markov chain                             State space

 

 

 

 

 

  • Initial distribution
     
  • Sub-transition matrix
     
  • Exit rates

 

\alpha
T
t = -T 1
t
\tau = \inf_t \{ X_t = \dagger \}
( X_t )_{t \ge 0}
\{1, ..., p, \dagger \}
\Leftrightarrow \tau \sim \mathrm{PhaseType}(\alpha, T)
\overline{T} = \left( \begin{matrix} T & t \\ 0 & 0 \end{matrix} \right)

Phase-type properties

 

 

Matrix exponential

 

Density and tail

 

 

Moments

 

 

M.g.f

f_\tau(s) = \alpha^\top \mathrm{e}^{T s} t
\mathrm{e}^{T s} = \sum_{i=0}^\infty \frac{(T s)^i}{i!}
\tau \sim \mathrm{PhaseType}(\alpha, T)
\overline{F}_\tau(s) = \alpha^\top \mathrm{e}^{T s} 1
\mathbb{E}[\tau] = {-}\alpha^\top T^{-1} 1
\mathbb{E}[\tau^n] = (-1)^n n! \,\, \alpha^\top T^{-n} 1
\mathbb{E}[\tau^n] = (-1)^n n! \,\, \alpha^\top T^{-n} 1

Phase-type generalises...

  • Exponential distribution


     
  • Sums of exponentials (Erlang distribution)




     
  • Mixtures of exponentials (hyperexponential distribution)
\alpha = \left( 1 \right), T = \left( -\lambda \right), t = \left( \lambda \right)
\alpha = \left( \begin{matrix} 1 \\ 0 \\ 0 \end{matrix} \right) , T = \left( \begin{matrix} -\lambda_1 & \lambda_1 & 0 \\ 0 & -\lambda_2 & \lambda_2 \\ 0 & 0 & -\lambda_3 \end{matrix} \right) , t = \left( \begin{matrix} 0 \\ 0 \\ \lambda_3 \end{matrix} \right)
\alpha = \left( \begin{matrix} \alpha_1 \\ \alpha_2 \\ \alpha_3 \end{matrix} \right) , T = \left( \begin{matrix} -\lambda_1 & 0 & 0 \\ 0 & -\lambda_2 & 0 \\ 0 & 0 & -\lambda_3 \end{matrix} \right) , t = \left( \begin{matrix} \lambda_1 \\ \lambda_2 \\ \lambda_3 \end{matrix} \right)

Class of phase-types is dense

S. Asmussen (2003), Applied Probability and Queues, 2nd Edition, Springer

More cool properties

Closure under addition, minimum, maximum

(\tau \mid \tau > s) \sim \mathrm{PhaseType}(\alpha_s, T)
\tau_i \sim \mathrm{PhaseType}(\alpha_i, T_i)
\Rightarrow \tau_1 + \tau_2 \sim \mathrm{PhaseType}(\dots, \dots)
\Rightarrow \min\{ \tau_1 , \tau_2 \} \sim \mathrm{PhaseType}(\dots, \dots)
\alpha_s^\top = \overline{F}_\tau(s)^{-1} \alpha^\top \mathrm{e}^{T s}

... and under conditioning

Erlangization/Canadization

T \in \mathbb{R} \qquad \tau_n \sim \mathrm{Erlang}(n, n/T)
\tau_n \overset{\mathbb{P}}{\longrightarrow} T \qquad \text{as } n \to \infty

Phase-type can even approximate a constant!

Representation is not unique

\alpha = ( 1, 0, 0 )^\top
T_1 = \left( \begin{matrix} -1 & 1 & 0 \\ 0 & -2 & 2 \\ 0 & 0 & -3 \end{matrix} \right)
T_2 = \left( \begin{matrix} -3 & 3 & 0 \\ 0 & -2 & 2 \\ 0 & 0 & -1 \end{matrix} \right)
\tau_1 \sim \mathrm{PhaseType}(\alpha, T_1)
\tau_2 \sim \mathrm{PhaseType}(\alpha, T_2)
\tau_1 \overset{\mathscr{D}}{=} \tau_2

Also, not easy to tell if any parameters produce a valid distribution

Lots of parameters to fit

  • General



     
  • Coxian distribution



     
  • Generalised Coxian distribution
\alpha = \left( \begin{matrix} 1 \\ 0 \\ 0 \end{matrix} \right) , \quad T = \left( \begin{matrix} -\lambda_1 & \lambda_{12} & 0 \\ 0 & -\lambda_2 & \lambda_{23} \\ 0 & 0 & -\lambda_3 \end{matrix} \right)
\alpha = \left( \begin{matrix} \alpha_1 \\ \alpha_2 \\ \alpha_3 \end{matrix} \right) , \quad T = \left( \begin{matrix} -\lambda_1 & \lambda_{12} & 0 \\ 0 & -\lambda_2 & \lambda_{23} \\ 0 & 0 & -\lambda_3 \end{matrix} \right)
\alpha = \left( \begin{matrix} \alpha_1 \\ \alpha_2 \\ \alpha_3 \end{matrix} \right) , \quad T = \left( \begin{matrix} -\lambda_1 & \lambda_{12} & \lambda_{13} \\ \lambda_{21} & -\lambda_2 & \lambda_{23} \\ \lambda_{31} & \lambda_{32} & -\lambda_3 \end{matrix} \right)
p(p+1)-1
2p-1
3p-2

Generalised Coxian

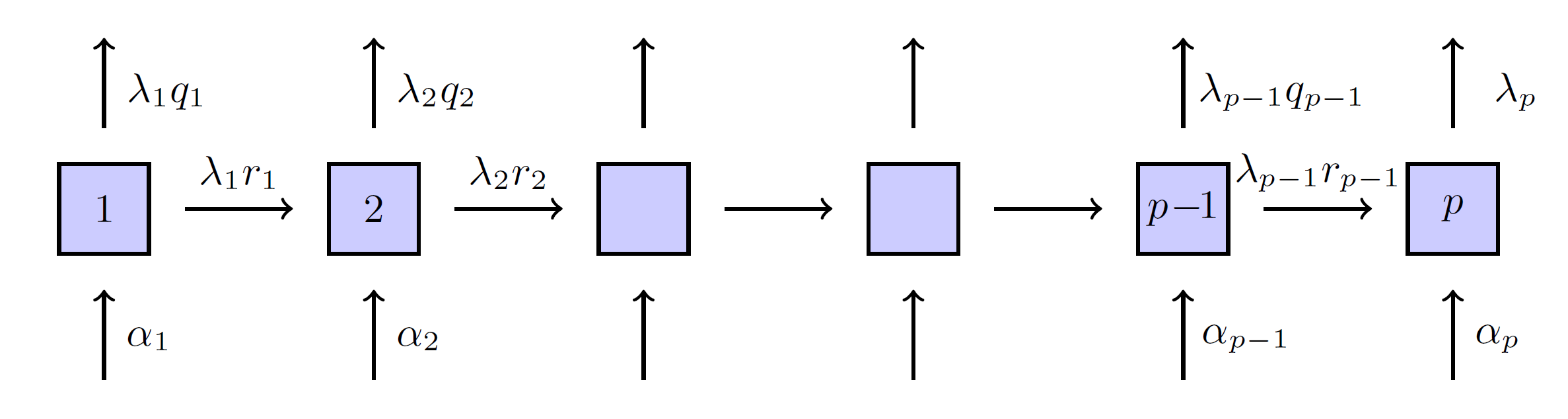
Two ways to view the phases

As meaningless mathematical artefacts

Choose number of phases to balance accuracy and over-fitting

As states which reflect some part of reality

Choose number of phases to match reality

X.S. Lin & X. Liu (2007) Markov aging process and phase-type law of mortality.
N. Amer. Act J. 11, pp. 92-109

M. Govorun, G. Latouche, & S. Loisel (2015). Phase-type aging modeling for health dependent costs. Insurance: Mathematics and Economics, 62, pp. 173-183.

Valuing equity-linked life insurance products

  • Say the customer lives for         years
  • Payout at death is linked to equity 
  • Example:
    • Guaranteed Minimum Death Benefit
       
    • High Water Benefit
       
  • Need
\tau
S_t
\max( S_{\tau}, K )
\overline{S}_\tau = \max_{t \le \tau} S_t
\mathbb{E}[ \mathrm{e}^{-\delta \tau} \Psi(\overline{S}_\tau, S_\tau) ]

Simplest model

Assume:

  •        is exponentially distributed
     
  •                           where              is a Brownian motion

 

Then              and                              are independent and exponentially distributed with rates

 

\tau
S_t = \mathrm{e}^{X_t}
X_t
\overline{X}_\tau
\overline{X}_\tau - X_\tau
\lambda_{\pm} = \mp \frac{\mu}{\sigma^2} + \sqrt{ \frac{\mu^2}{\sigma^4} + \frac{2\lambda}{\sigma^2} }

Wiener-Hopf Factorisation

\mathbb{P}(\overline{X}_\tau \in \mathrm{d}x, X_\tau - \overline{X}_\tau \in \mathrm{d}y) = \mathbb{P}(\overline{X}_\tau \in \mathrm{d}x) \mathbb{P}(\underline{X}_\tau \in \mathrm{d}y)
X_t
  •        is an exponential random variable
     
  •         is a Lévy process
\tau

Doesn't work for non-random time

\mathbb{P}(\overline{X}_t \in \mathrm{d}x, X_t - \overline{X}_t \in \mathrm{d}y \mid \overline{\sigma}_t = s)
= \mathbb{P}(\overline{X}_t \in \mathrm{d}x \mid \overline{\sigma}_t = s) \mathbb{P}(\underline{X}_t \in \mathrm{d}y \mid \underline{\sigma}_t = t - s)

Motivating theory

Accepted to Stochastic Models

Can read on https://arxiv.org/pdf/1803.00273.pdf

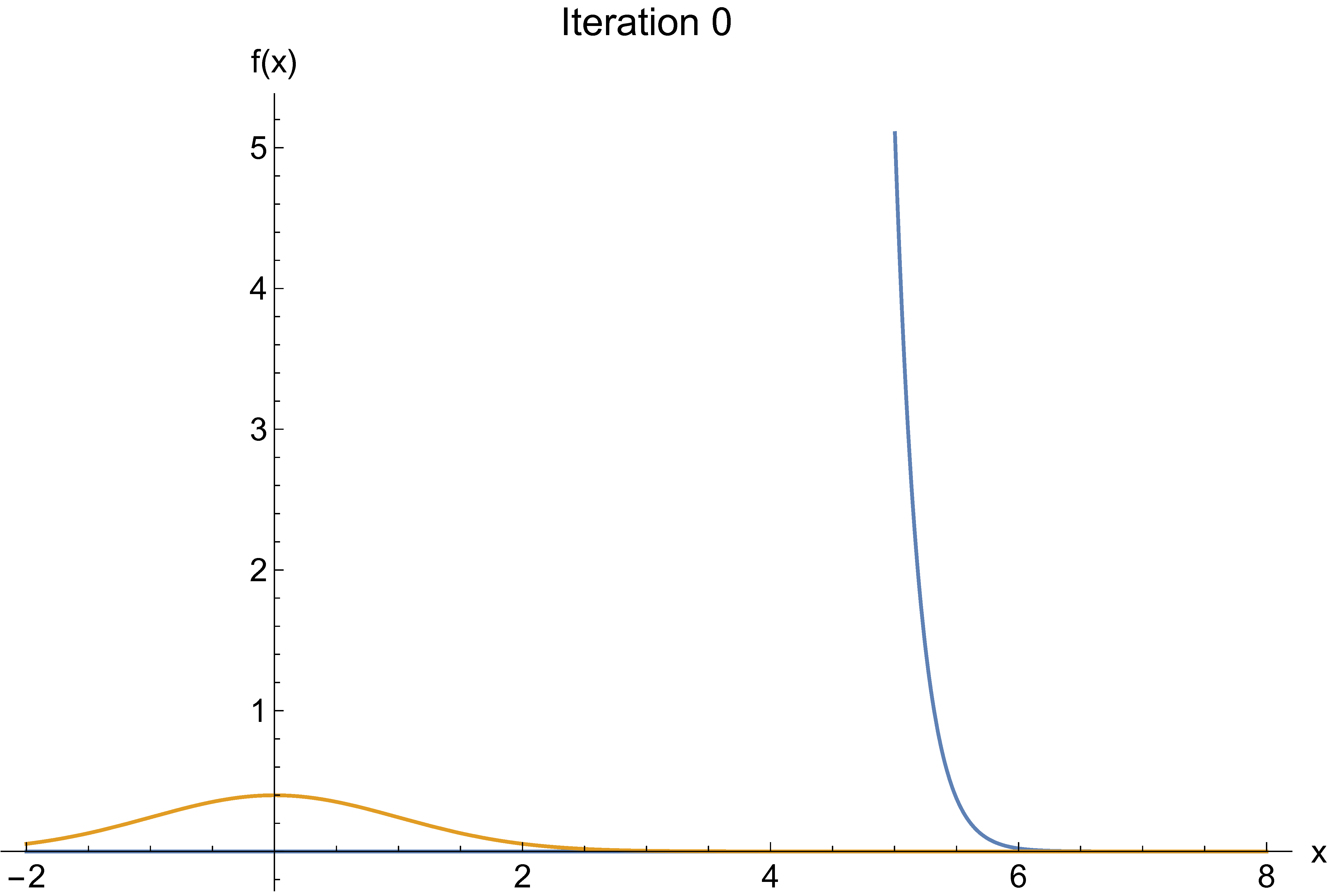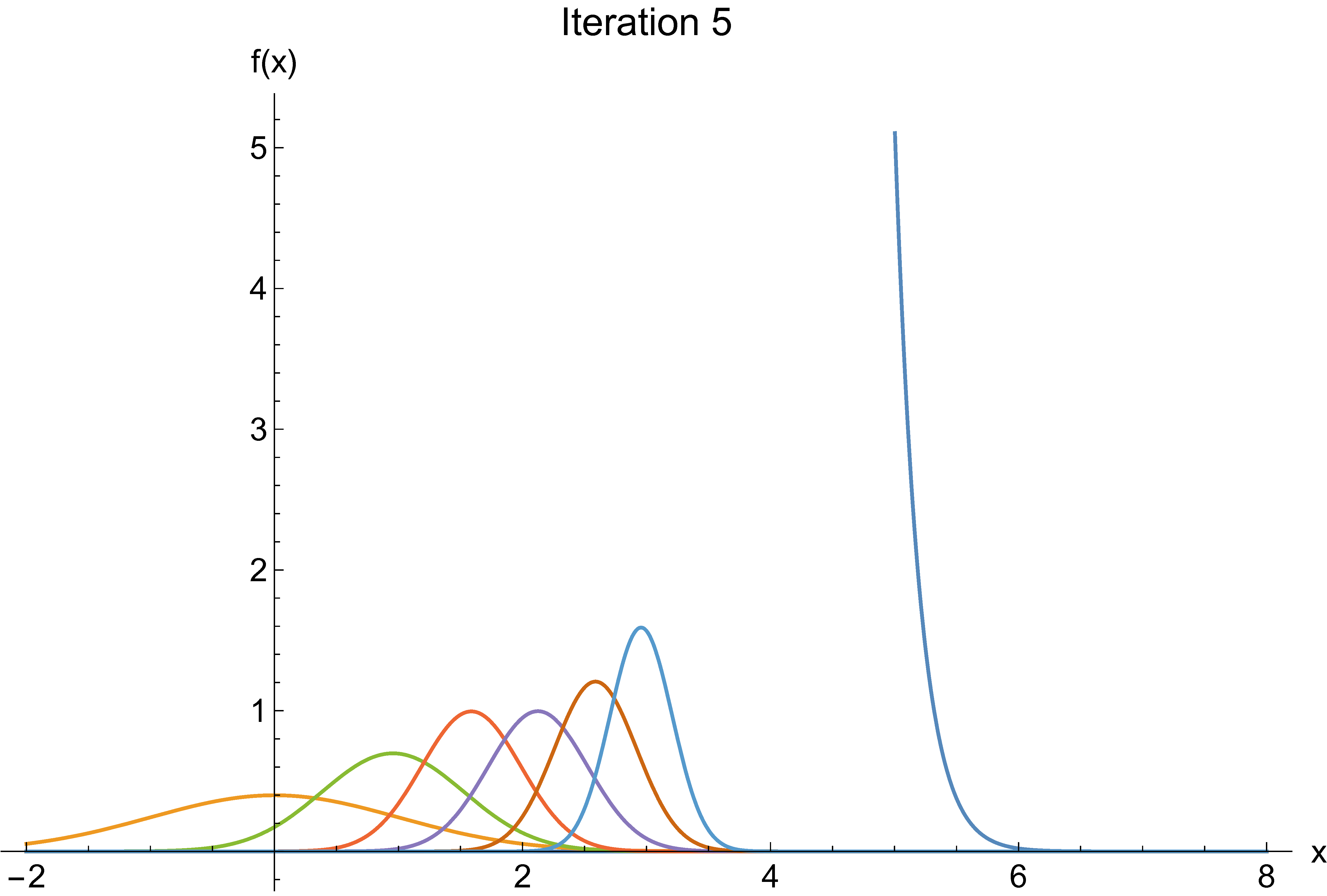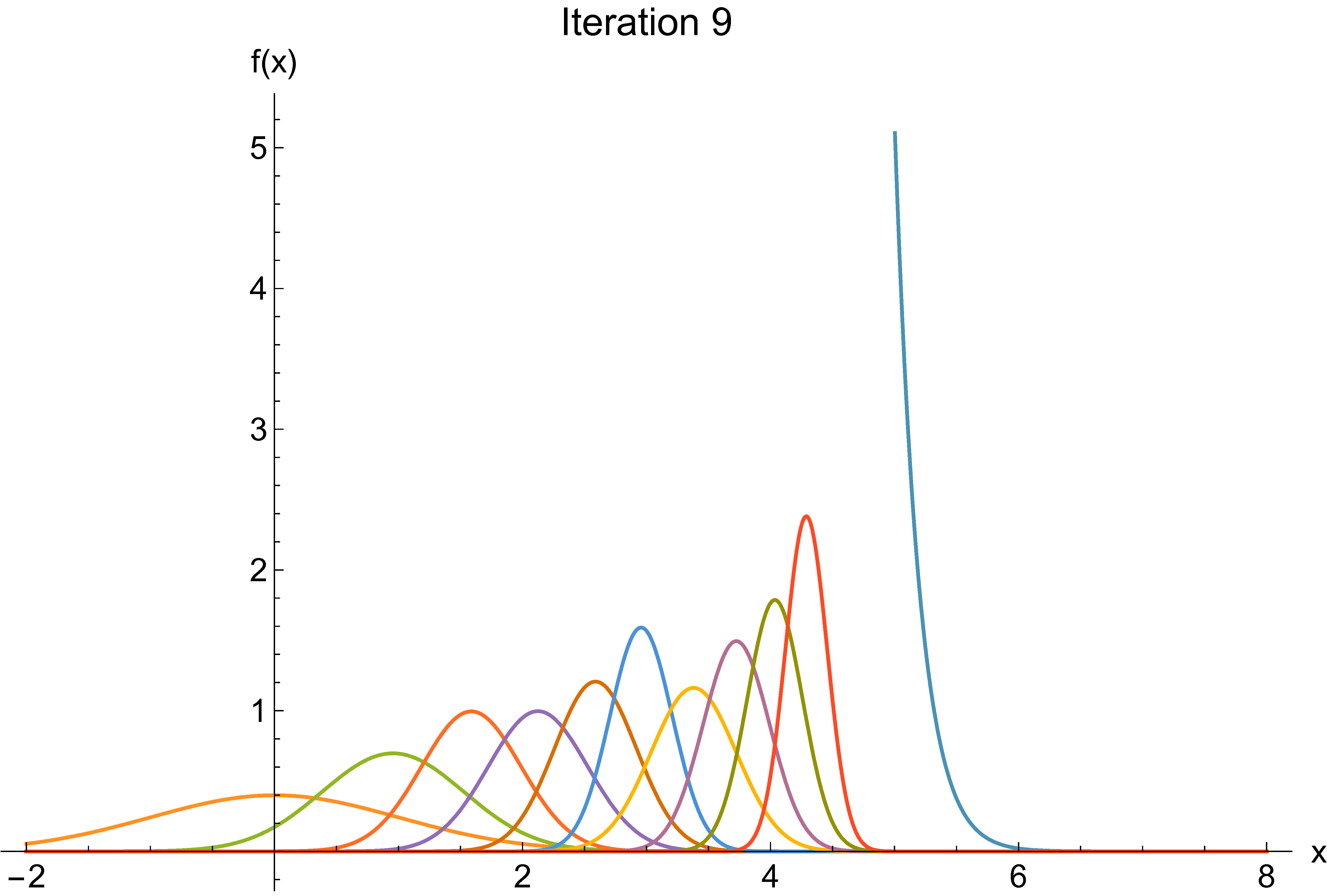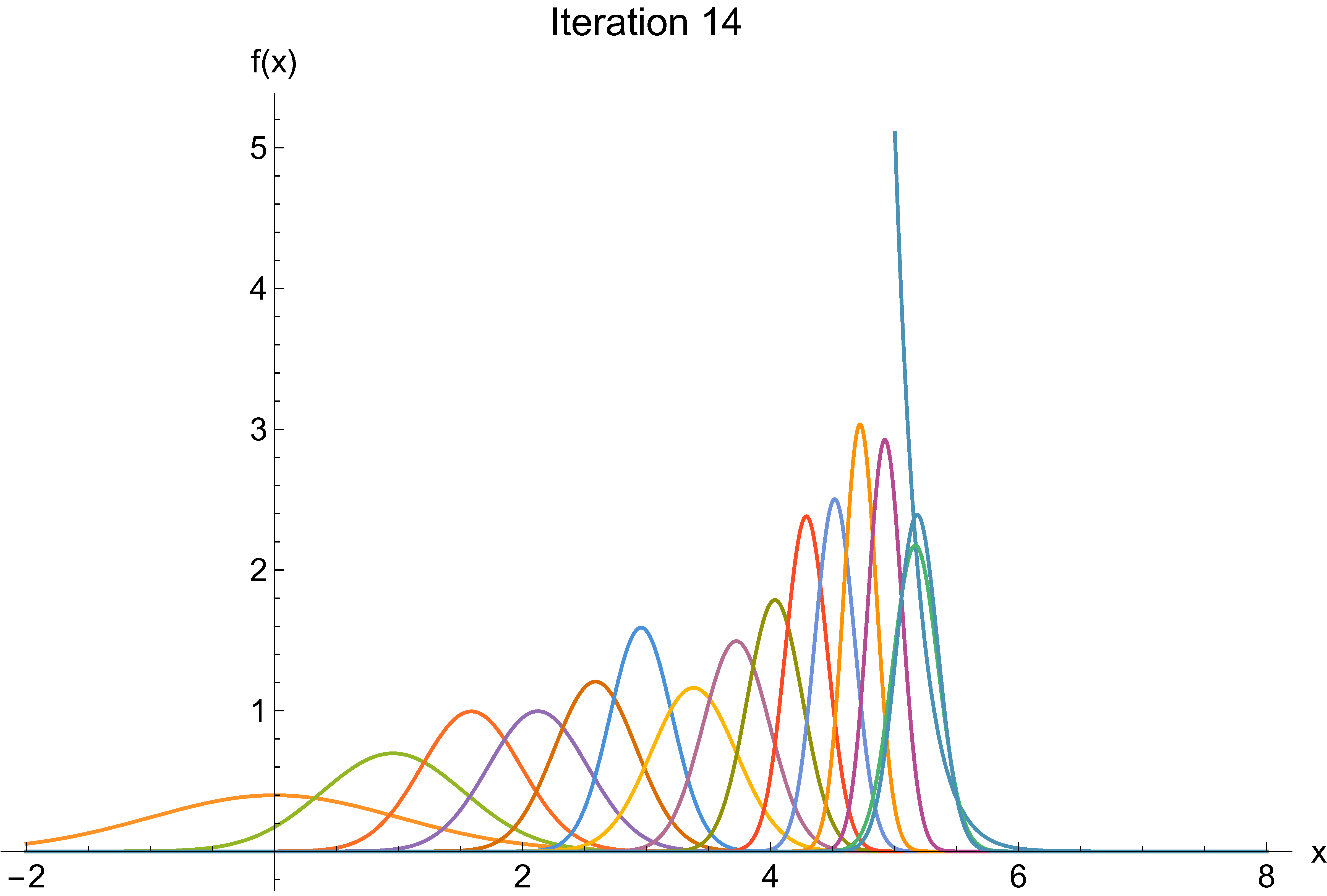
First attempts with EMpht

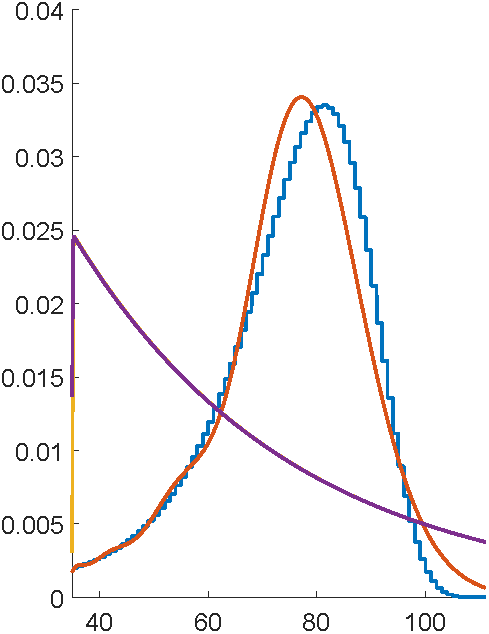
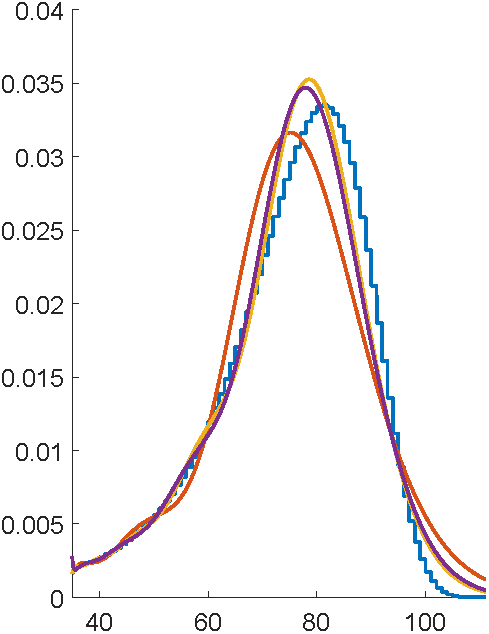
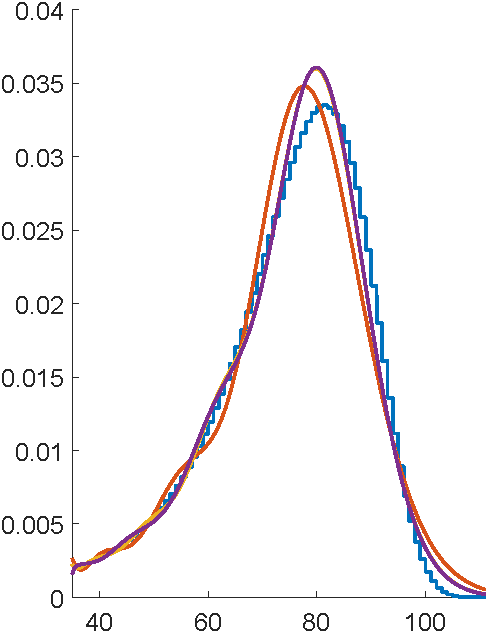
5 hours compute time

This is ancient technology...

Dennis Ritchie (creator of C) standing by the computer used to create C, 1972

Diving into the source

c(y ; i \mid \alpha, T) = \int_0^y \alpha^\top \mathrm{e}^{T u} e_i \cdot \mathrm{e}^{T (y-u)} t \,\, \mathrm{d} u
i = 1, \dots, p
  • Single threaded
  • Homegrown matrix handling (e.g. all dense)
  • Computational "E" step




     
  • Instead solve a large system of DEs


     
  • Hard to read or modify (e.g. random function)
     
c'(y ; i \mid \alpha, T) = T c(y ; i \mid \alpha, T) + [ \alpha^ \top \mathrm{e}^{T y} ]_i t
p(p+2)

Rewrite in Julia

void rungekutta(int p, double *avector, double *gvector, double *bvector,
		double **cmatrix, double dt, double h, double **T, double *t,
		double **ka, double **kg, double **kb, double ***kc)
{
  int i, j, k, m;
  double eps, h2, sum;

  i = dt/h;
  h2 = dt/(i+1);
  init_matrix(ka, 4, p);
  init_matrix(kb, 4, p);
  init_3dimmatrix(kc, 4, p, p);
  if (kg != NULL)
    init_matrix(kg, 4, p);
    ...
    for (i=0; i < p; i++) {
      avector[i] += (ka[0][i]+2*ka[1][i]+2*ka[2][i]+ka[3][i])/6;
      bvector[i] += (kb[0][i]+2*kb[1][i]+2*kb[2][i]+kb[3][i])/6;
      for (j=0; j < p; j++)
        cmatrix[i][j] +=(kc[0][i][j]+2*kc[1][i][j]+2*kc[2][i][j]+kc[3][i][j])/6;
    }
  }
}

This function: 116 lines of C, built-in to Julia

Whole program: 1700 lines of C, 300 lines of Julia 

# Run the ODE solver.
u0 = zeros(p*p)
pf = ParameterizedFunction(ode_observations!, fit)
prob = ODEProblem(pf, u0, (0.0, maximum(s.obs)))
sol = solve(prob, OwrenZen5())

https://github.com/Pat-Laub/EMpht.jl

DE solver going negative

# Run the ODE solver.
u0 = zeros(p*p)
pf = ParameterizedFunction(ode_observations!, fit)
prob = ODEProblem(pf, u0, (0.0, maximum(s.obs)))
sol = solve(prob, OwrenZen5())

...

u = sol(s.obs[k])
C = reshape(u, p, p)
if minimum(C) < 0
    (C,err) = hquadrature(p*p, (x,v) -> c_integrand(x, v, fit, s.obs[k]), 
                0, s.obs[k], reltol=1e-1, maxevals=500)
    C = reshape(C, p, p)
end

Swap to quadrature in Julia

Swap to quadrature in Julia

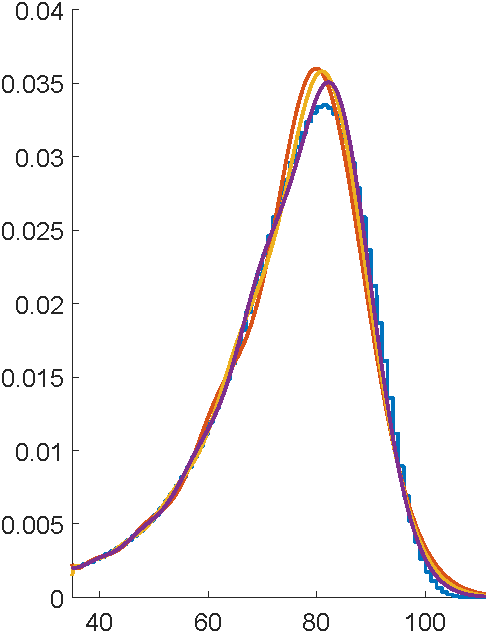
Rushing to complete

Submission deadline passes

Get to Lyon..

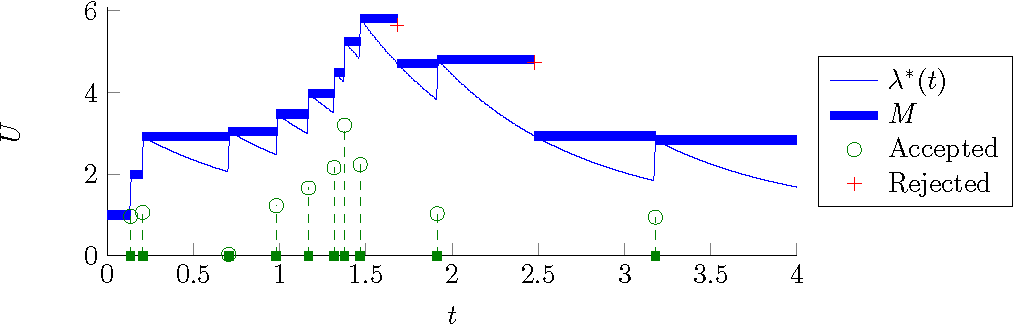
Uniformization magic

Uniformization magic

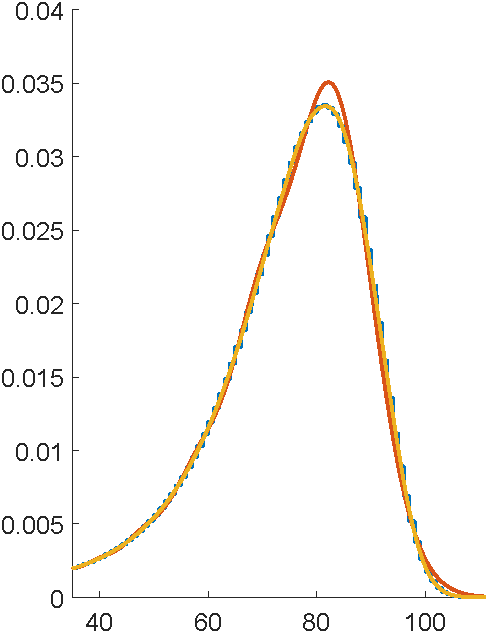
What was the point of all this again?

  • The customer lives for         years
  • Need
     
  • ... and we have it



    where
\mathbb{E}[ \mathrm{e}^{-\delta \tau} \Psi(\overline{S}_\tau, S_\tau) ]
\tau
= \mathbb{E}[ \mathrm{e}^{-\delta \tau} \Psi( S_0 \mathrm{e}^{\overline{X}_\tau}, S_0 \mathrm{e}^{X_\tau} ) ]
\mathbb{E} [\mathrm{e}^{-\delta\tau} f(\overline{X}_\tau)g(D_\tau) ] = \alpha^\top F_{U_\delta} \Delta_r G_{U^*_\delta }^{\top}{\alpha^*}^{\!\top}
G_{U^*_\delta} = \int_0^\infty g(y)\mathrm{e}^{U^*_\delta y}\,\mathrm{d} y
F_{U_\delta} = \int_0^\infty f(x) \mathrm{e}^{U_\delta x}\,\mathrm{d} x \,,

Another cool thing

\mathbb{E}[ \mathrm{e}^{-\delta (\tau \wedge T) } \Psi(\overline{S}_{\tau \wedge T}, S_{\tau \wedge T}) ]

Contract over a limited horizon

Can use Erlangization so

\tau_n \approx T \,, \quad \tau_n \sim \mathrm{Erlang}(n, n/T)
\tau \wedge \tau_n = \tau_n^* \sim \mathrm{PhaseType}(\dots, \dots)
\ldots \approx \mathbb{E}[ \mathrm{e}^{-\delta \tau_n^* } \Psi(\overline{S}_{\tau_n^*}, S_{\tau_n^*}) ]

and phase-type closure under minimums

What conclusion to draw?

... [Phase-types] are not well suited to approximating every distribution. Despite the fact that they are dense... the order of the approximating distribution may be disappointingly large... while the phase-type distributions are admittedly poorly suited to matching certain features, even low-order phase-type distributions do display a great variety of shapes...This rich family may be used in place of exponential distributions in many models without destroying our ability to compute solutions.

C.A. O'Cinneide (1999), Phase-type distributions: open problems and a few properties, Stochastic Models 15(4), p. 4

Made with Slides.com