Wyszukiwanie ścieżek w grafach - Algorytm A*
Algorytm a*
algorytm heurystyczny znajdowania najkrótszej ścieżki w grafie ważonym z dowolnego wierzchołka do wierzchołka spełniającego określony warunek zwany testem celu.
Algorytm a*
Algorytm A* od wierzchołka początkowego tworzy ścieżkę, za każdym razem wybierając wierzchołek x z dostępnych w danym kroku niezbadanych wierzchołków tak, by minimalizować funkcję f(x) zdefiniowaną:
f(x) = g(x) + h(x)
gdzie:
g(x) to droga pomiędzy wierzchołkiem początkowym a x. Dokładniej: suma wag krawędzi, które należą już do ścieżki plus waga krawędzi łączącej aktualny węzeł z x.
f(x) przewidywana przez heurystykę droga od x do wierzchołka docelowego.
W każdym kroku algorytm dołącza do ścieżki wierzchołek o najniższym współczynniku f. Kończy w momencie natrafienia na wierzchołek będący wierzchołkiem docelowym.
Algorytm a*
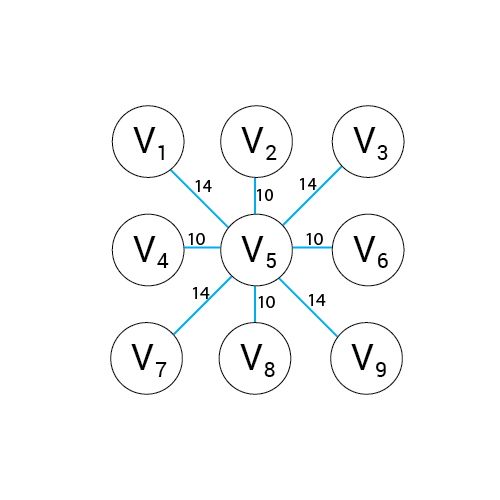
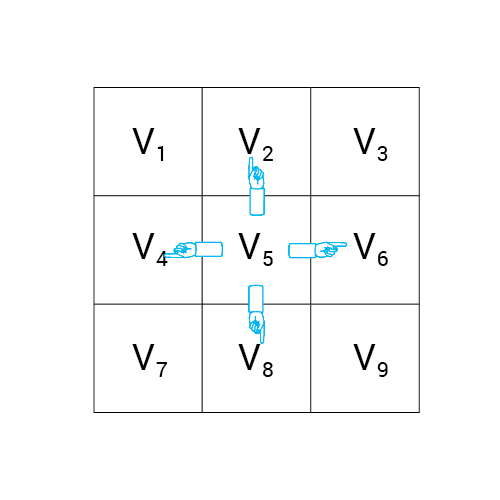
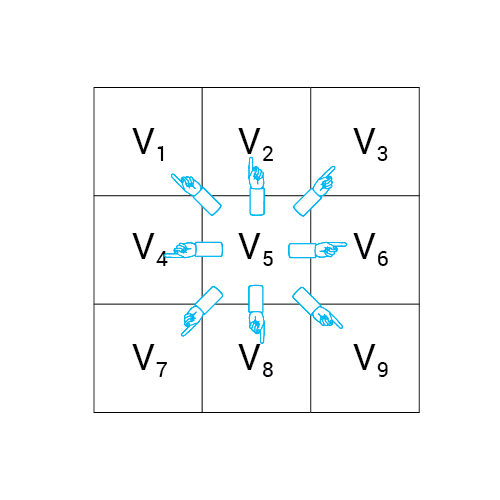
Algorytm a*

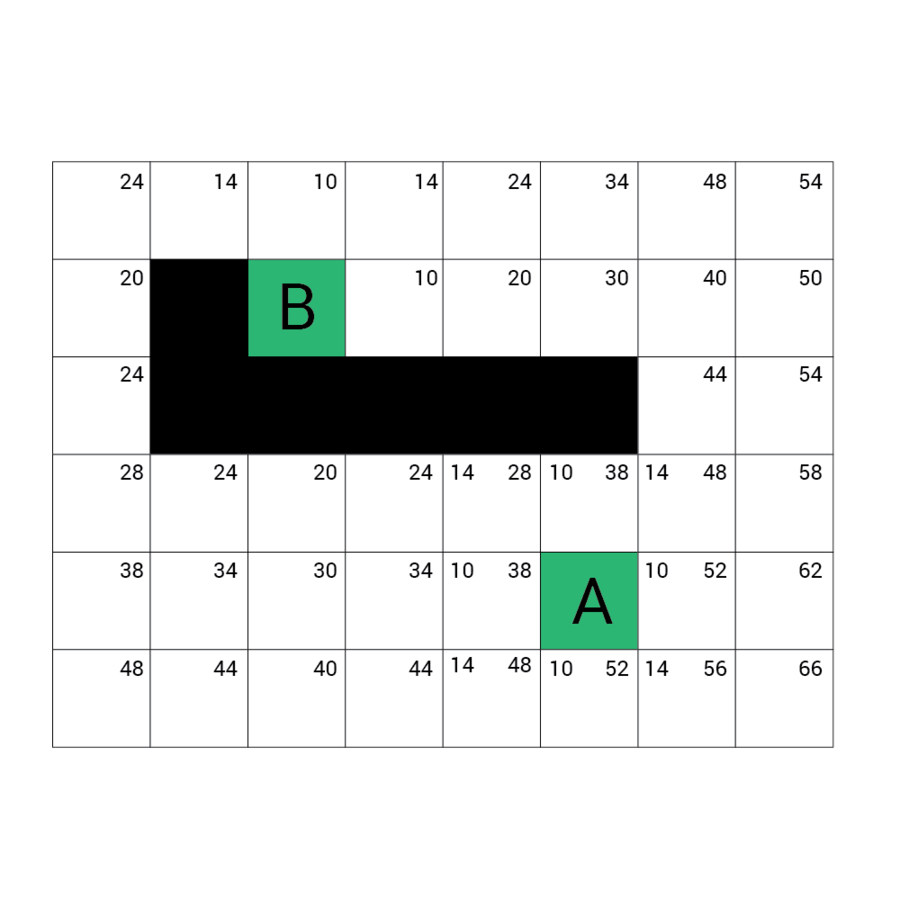
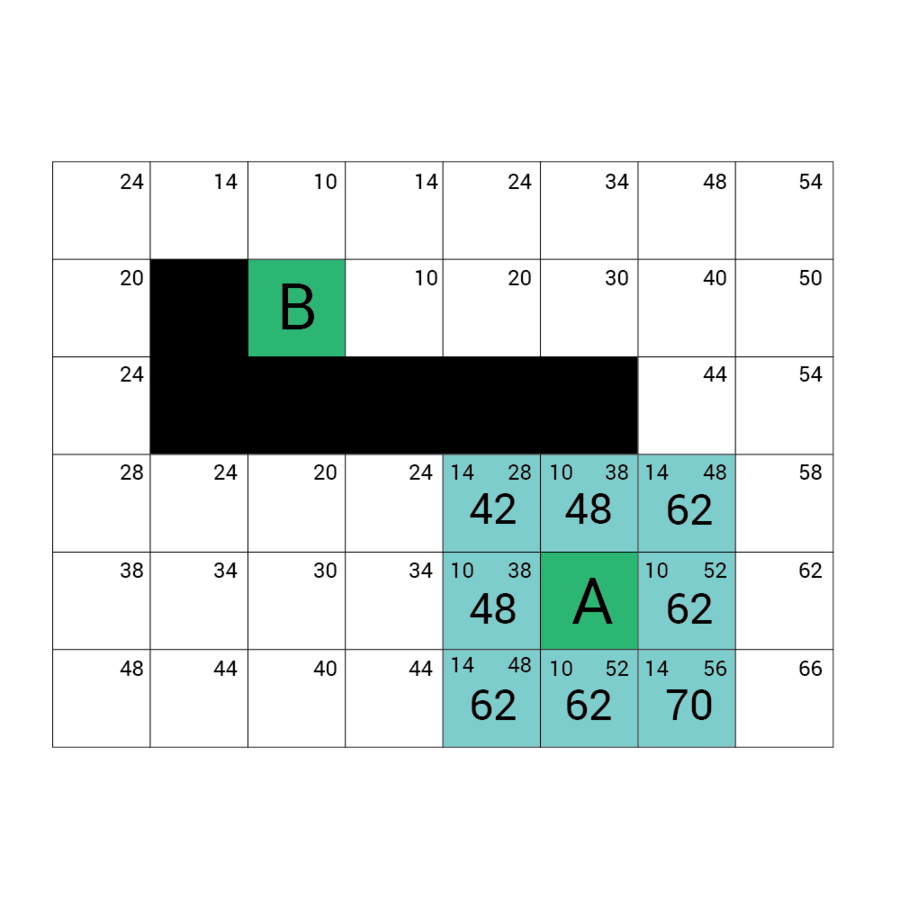
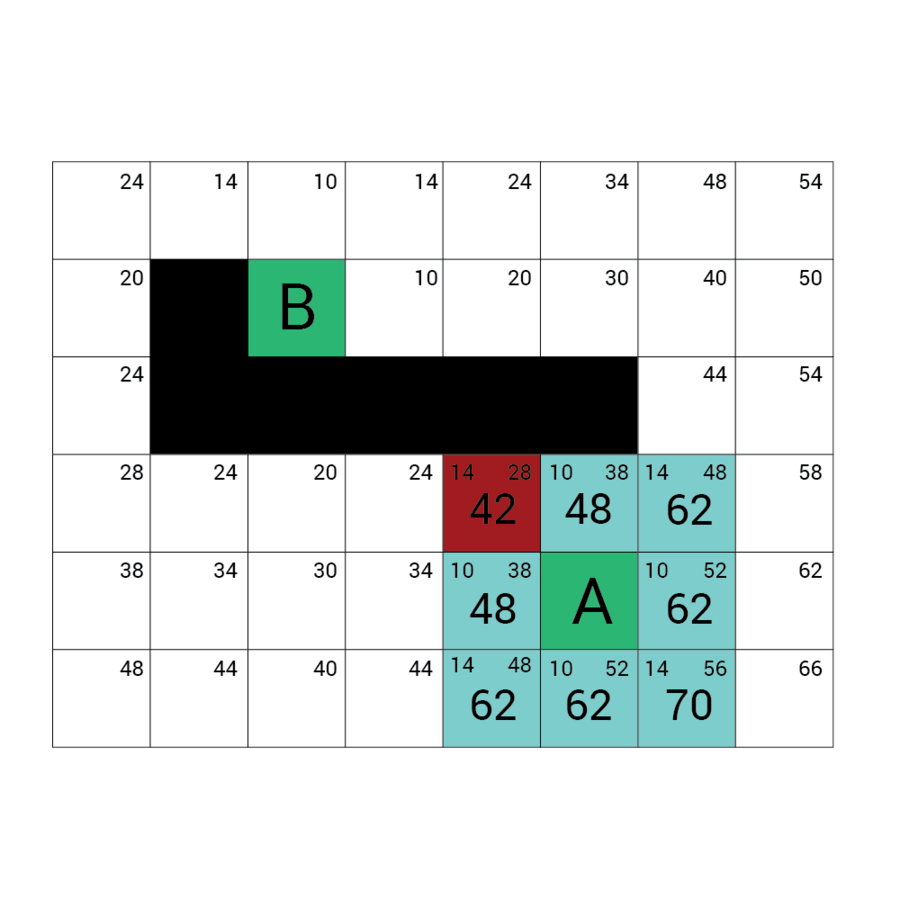
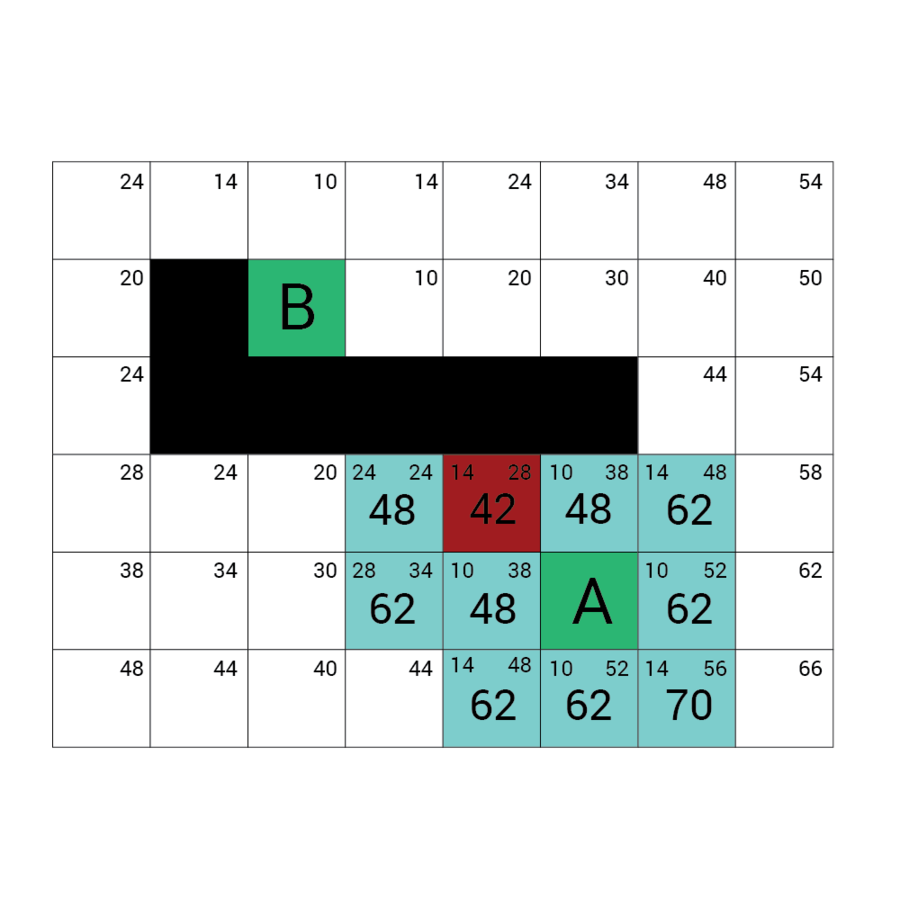
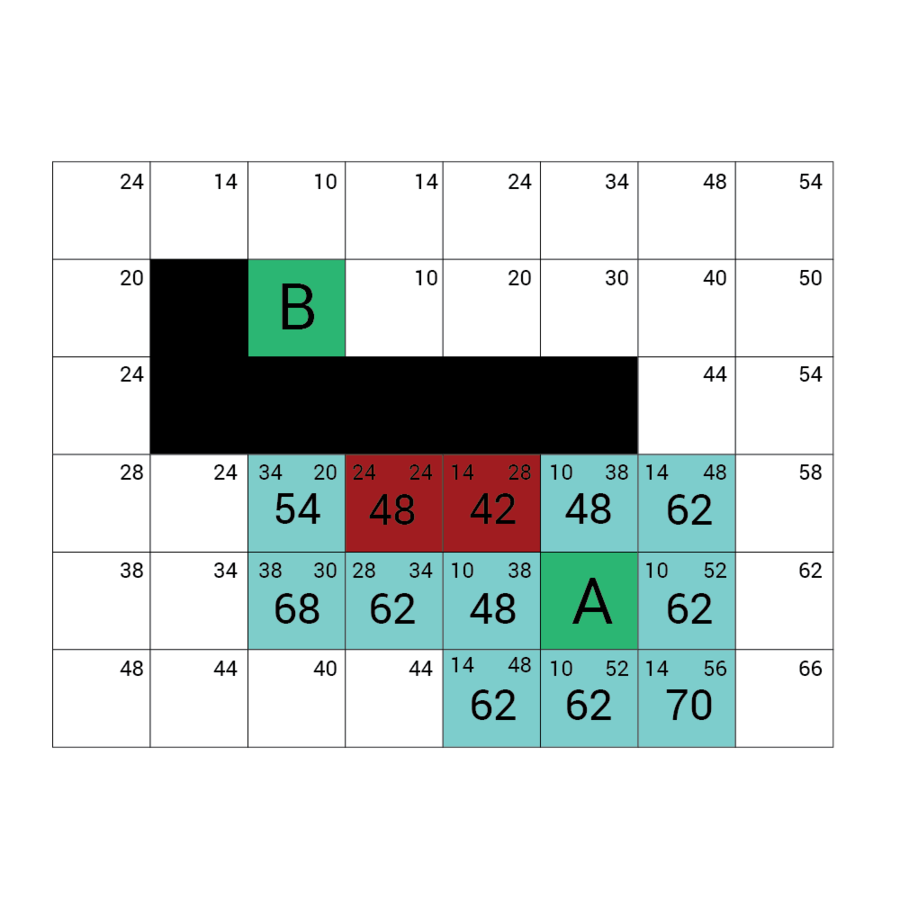
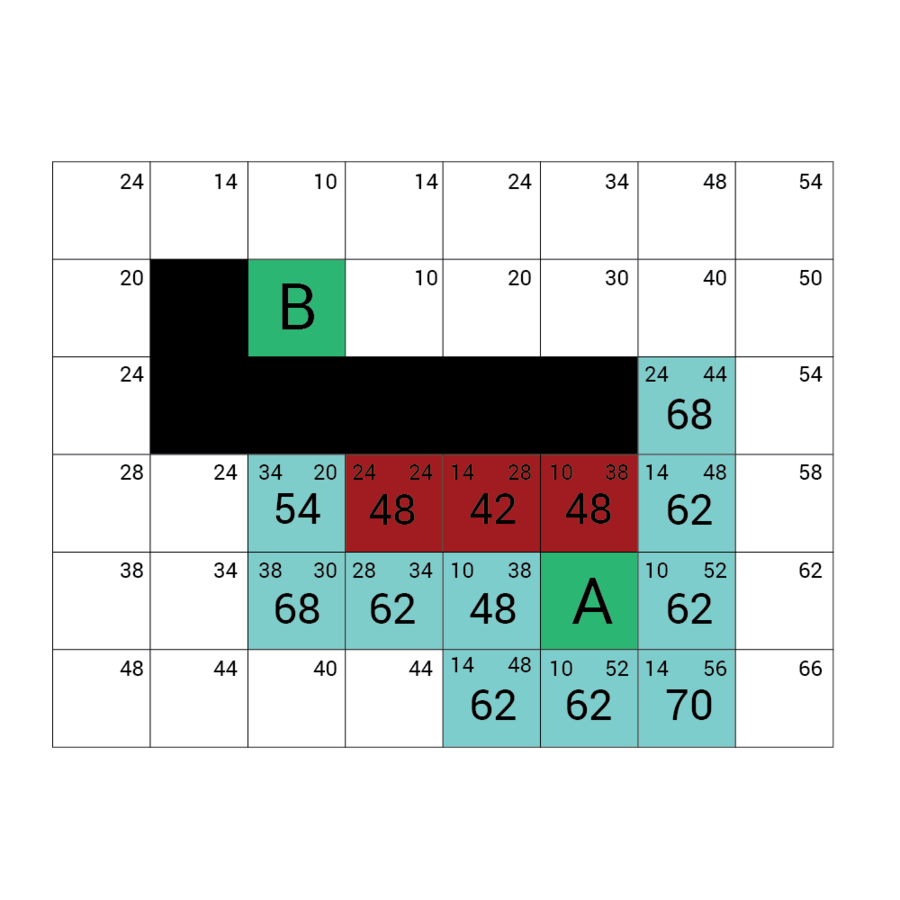
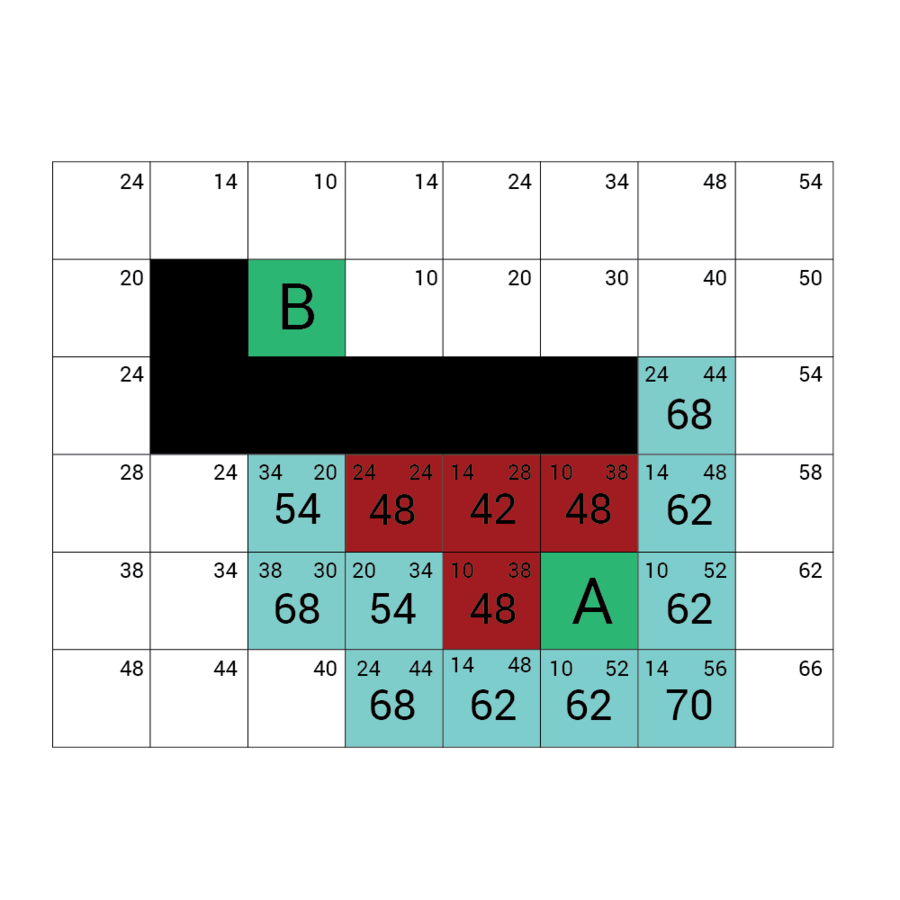
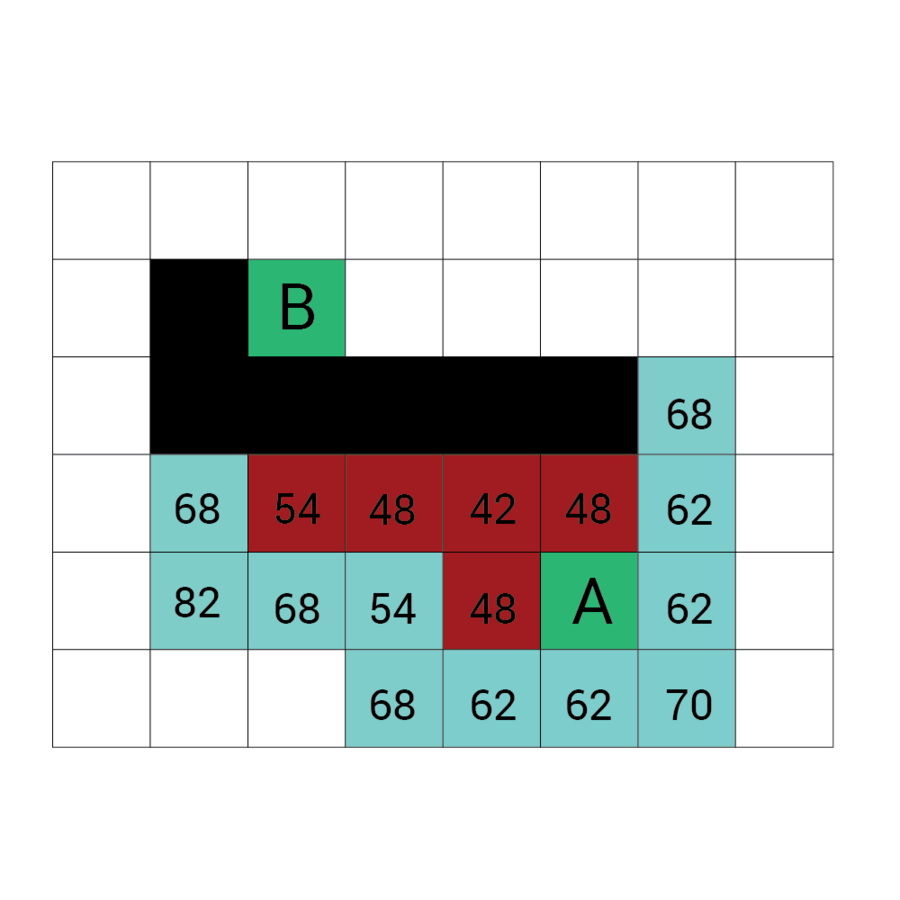
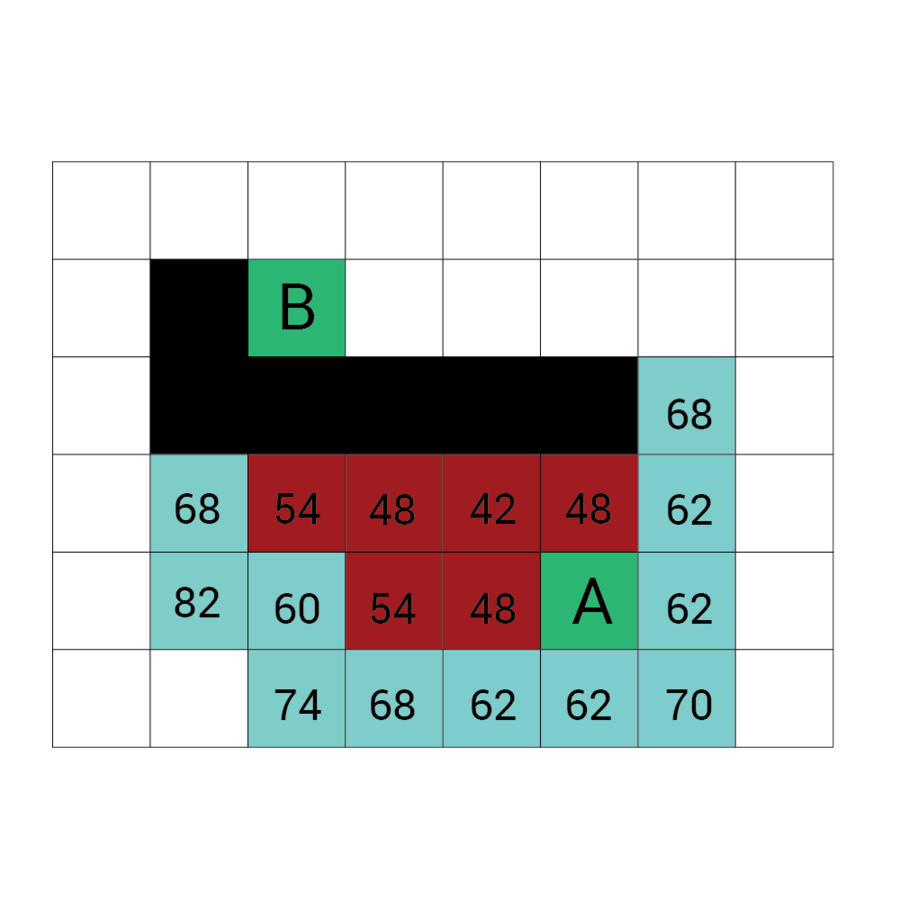
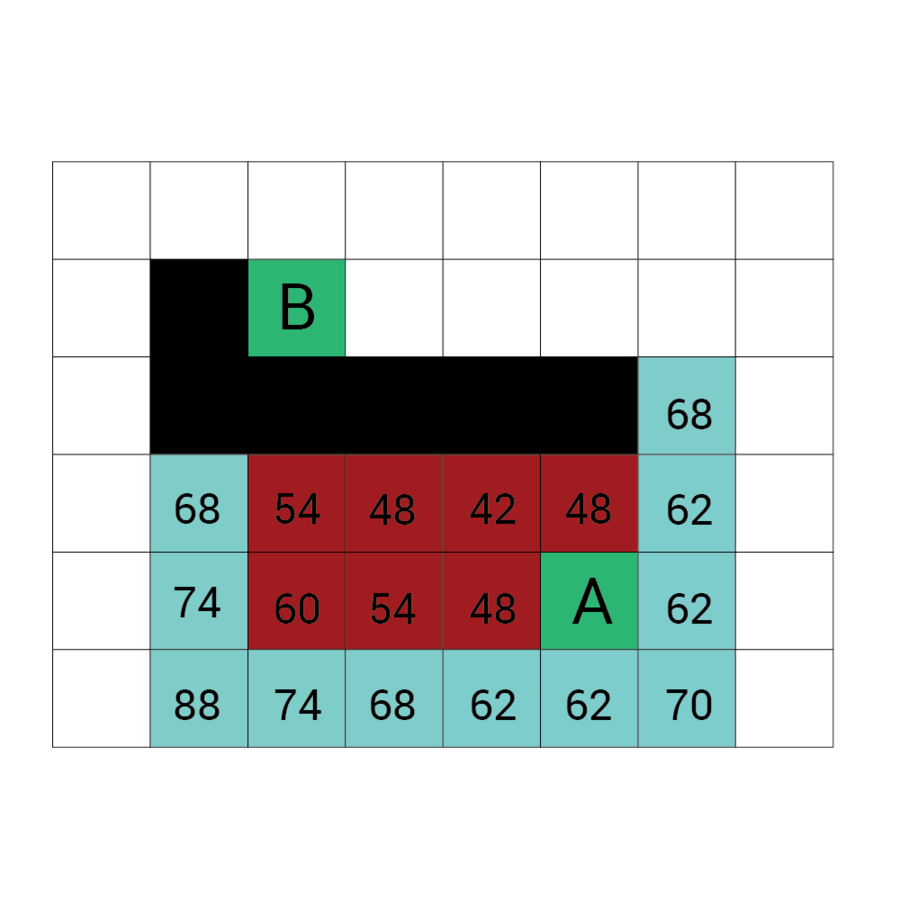
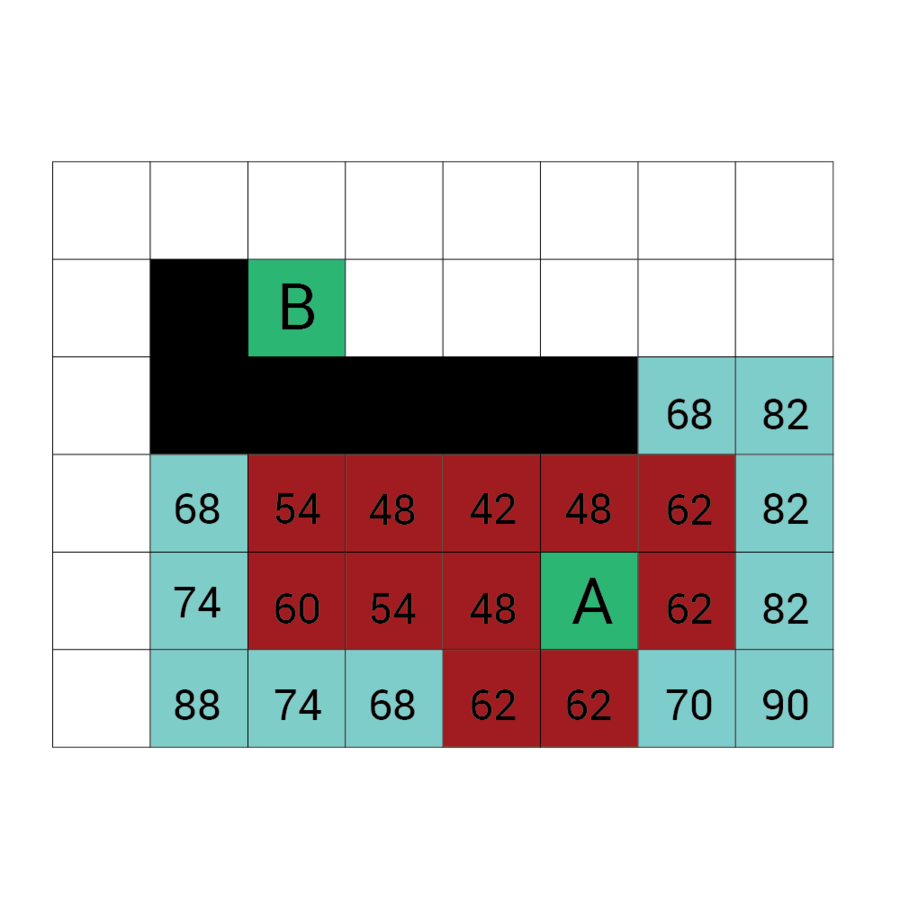
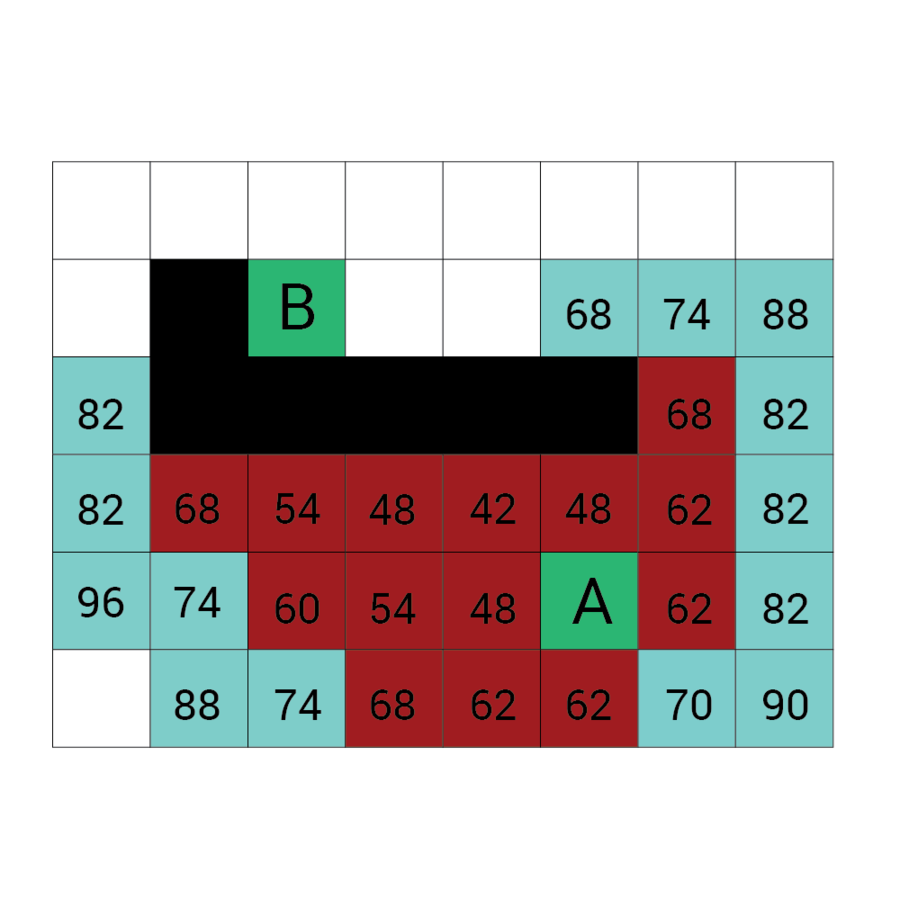
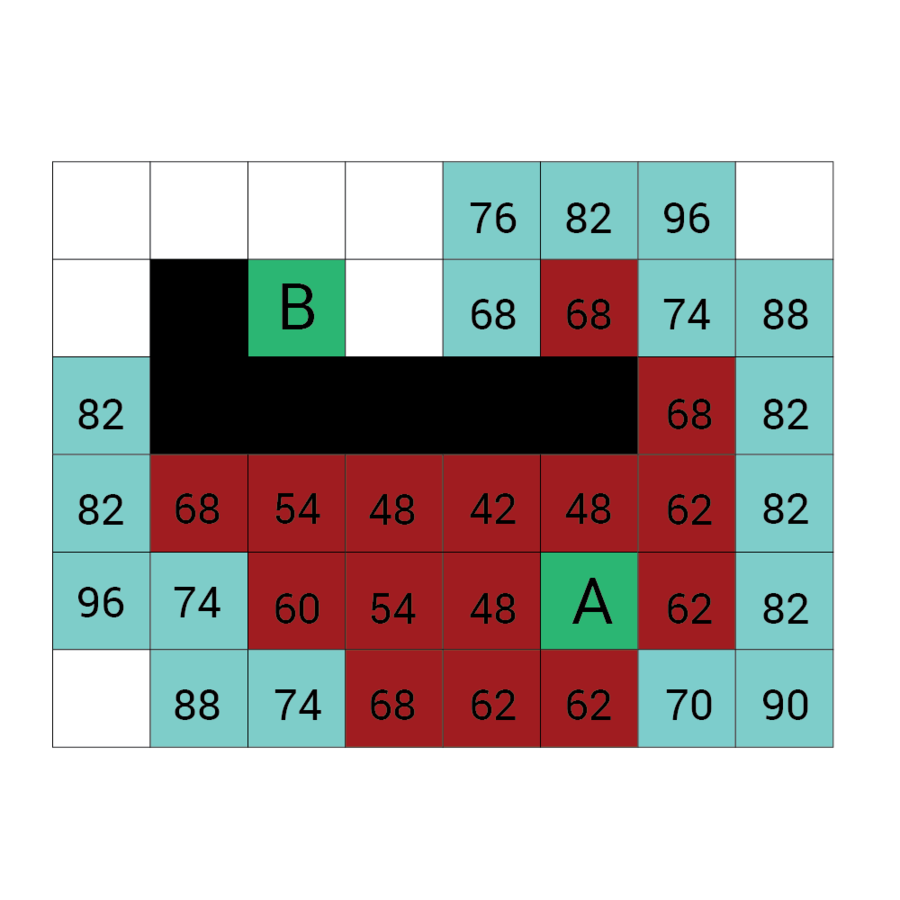
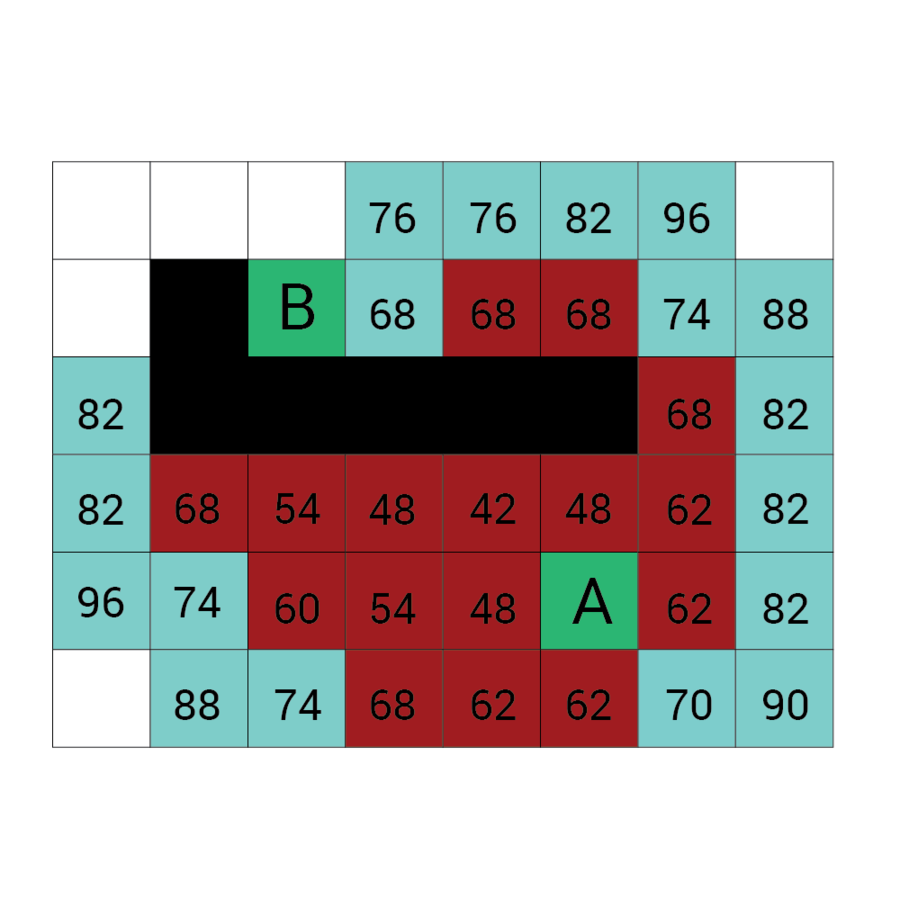
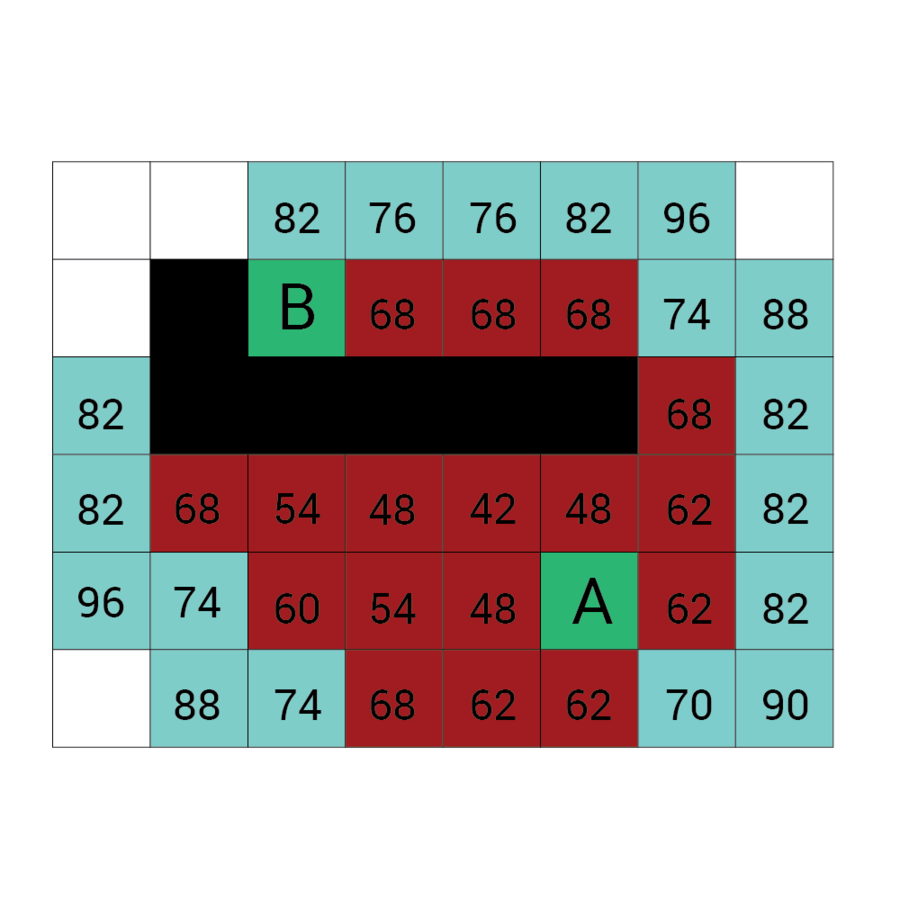
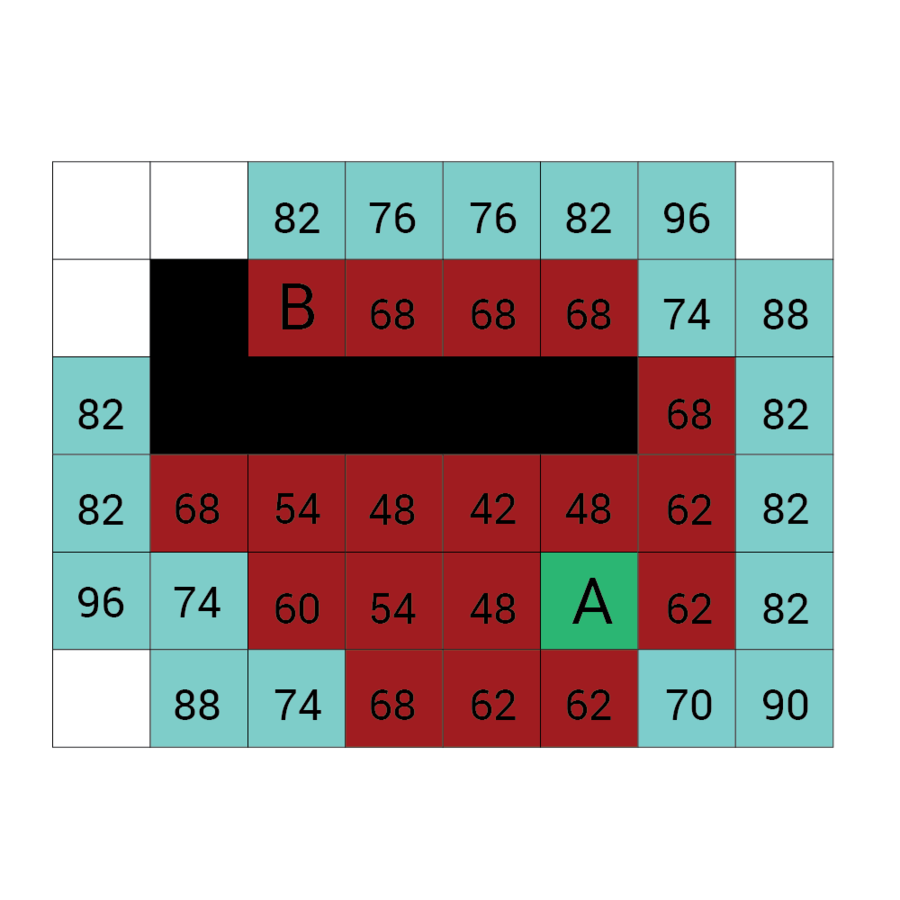
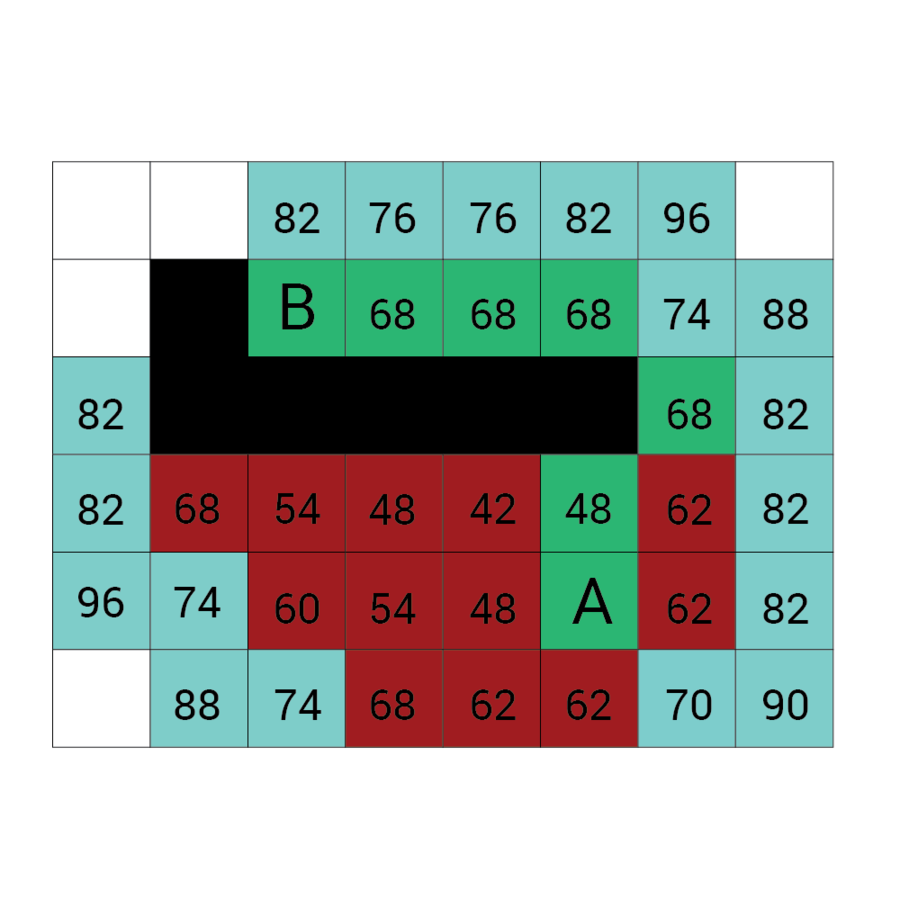
Wartość h
Wartość f
Wartość G
wartość H + wartość G
Odległość z A
Odległość z B
Algorytm a*
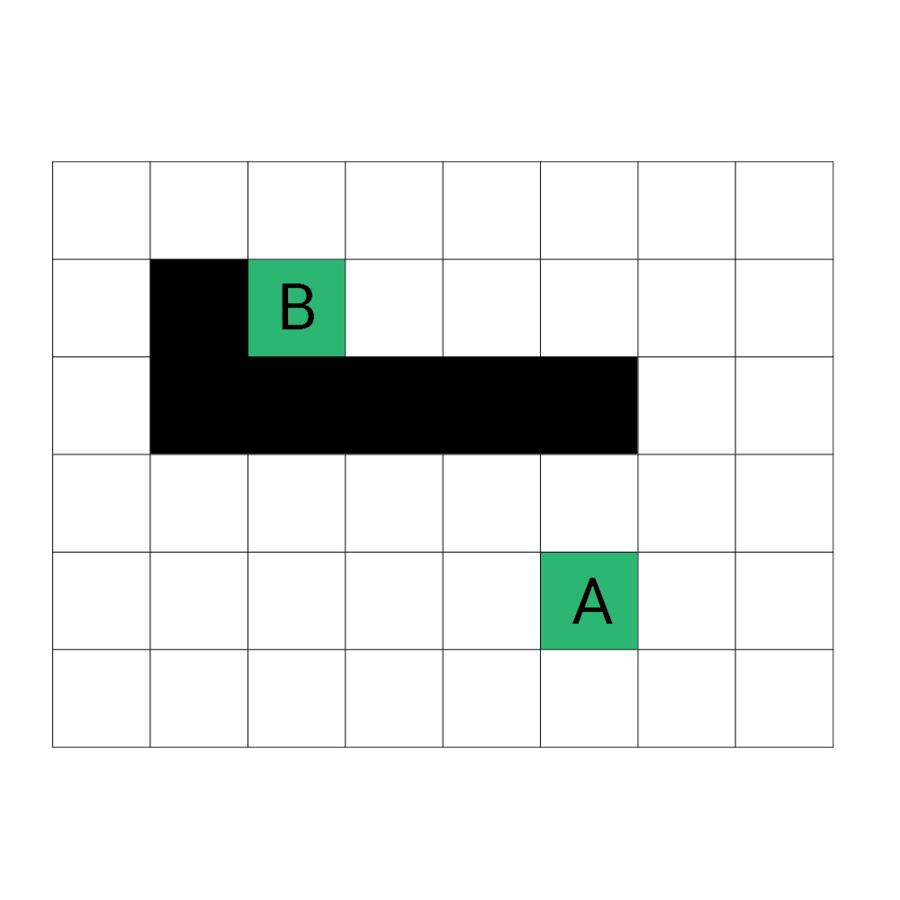
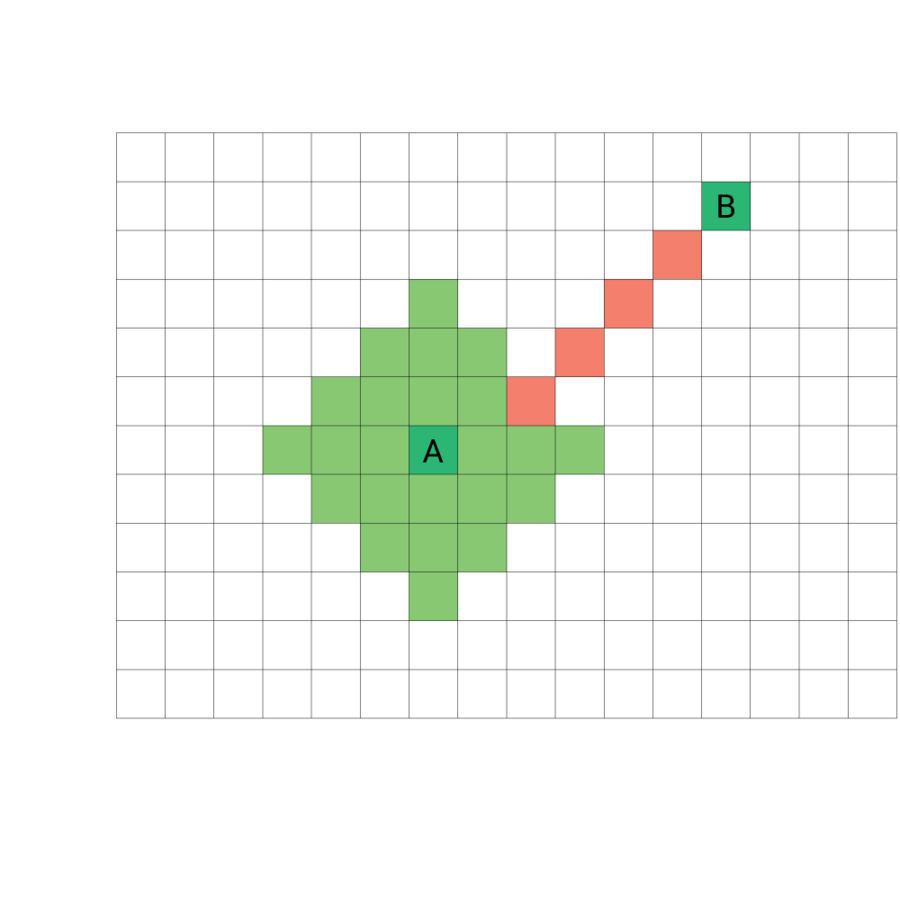
Przykłady
źródło: https://sebastian.itch.io/
Algorytm a*
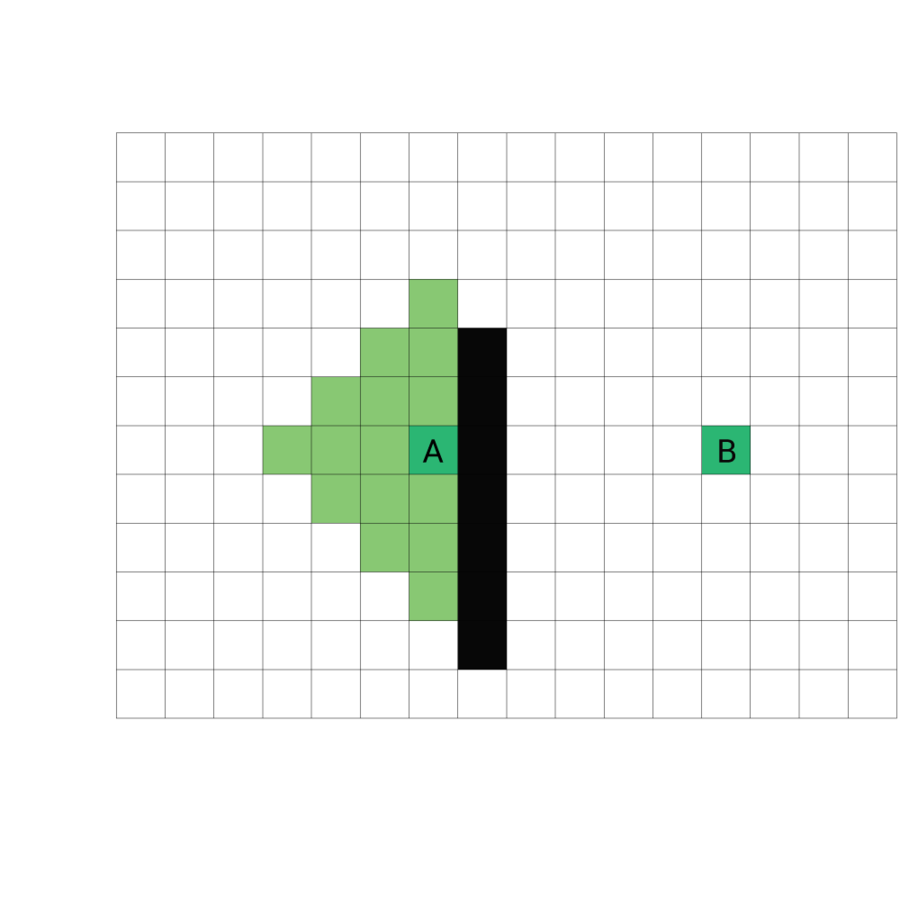
Przykłady
źródło: https://sebastian.itch.io/
Algorytm a*
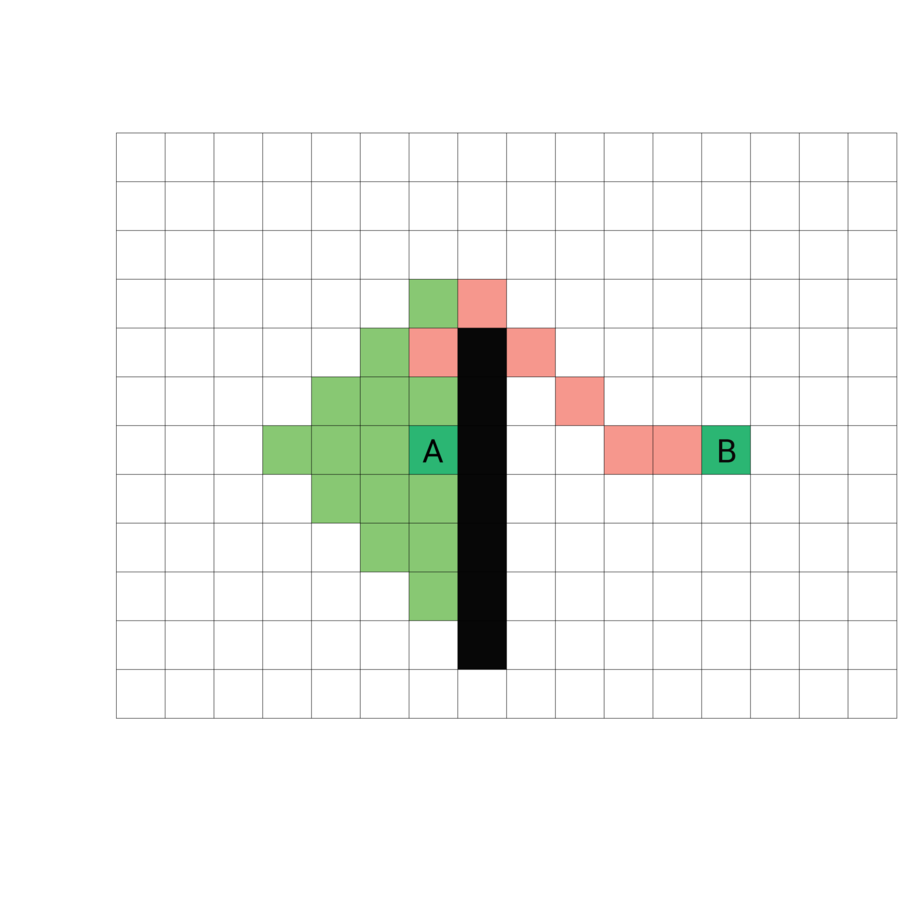
Przykłady
źródło: https://sebastian.itch.io/
Historia
W 1968 Nils Nilsson pracował nad udoskonaleniem wyszukiwania ścieżek w robocie Shakey.

Shakey to mobilny robot wielozadaniowy ogólnego wykorzystania.
Poruszał problemy robotyki, widzenia komputerowego i przetwarzania języka naturalnego
Rozwijany w latach 1966-1972.
Programowany w języku LIPS.
Historia
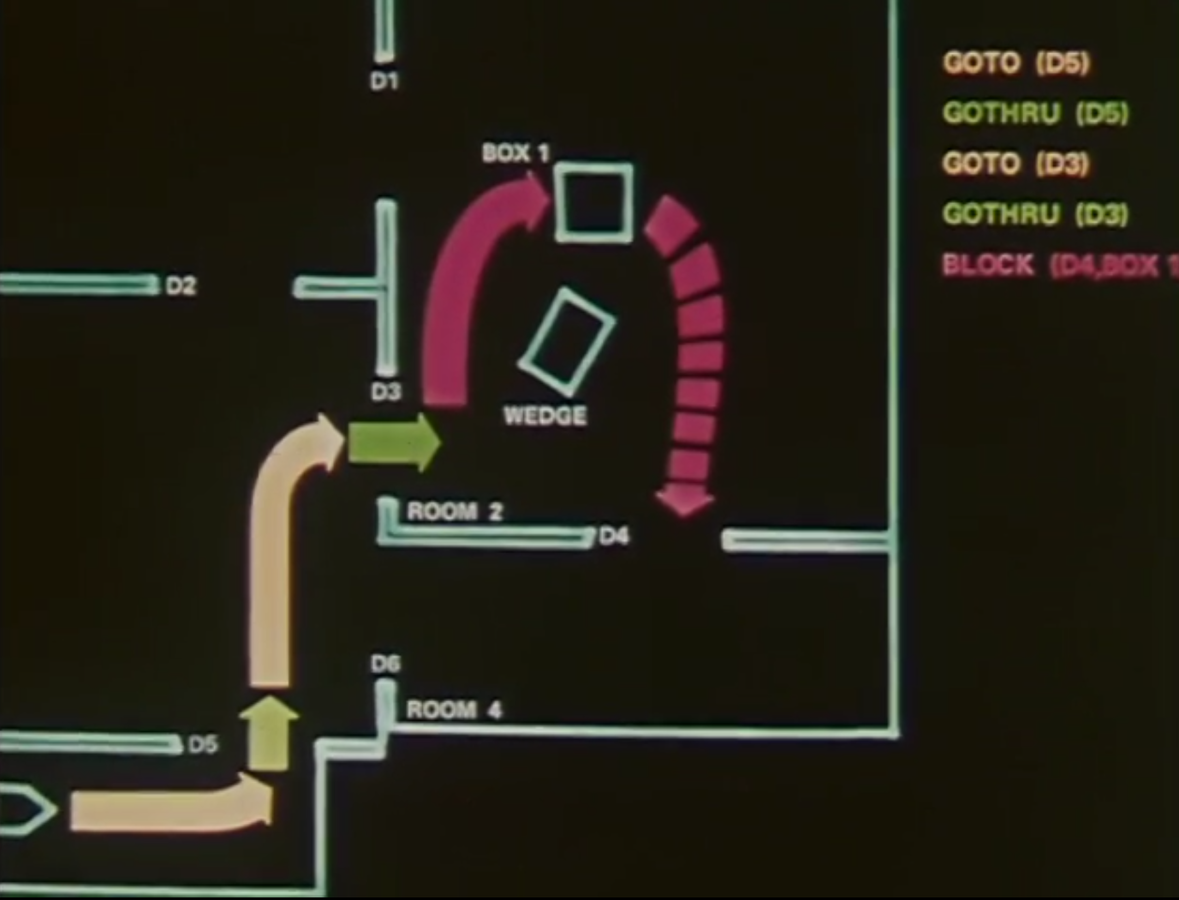
Potrafił przemieszczać się z jednego pokoju do drugiego, wyłączać i włączać światło w pomieszczeniu, zamykać i otwierać drzwi, wjeżdżać i zjeżdżać z powierzchni pochyłych przesuwać przedmioty i je omijać
Do pomiarów i prawidłowego
działania wykorzystywał
- antenę radiową
- sonar
- kamerę
- sensory kolizji
-silniczki sterujące kołami i kamerą
Historia
Podczas pierwszych badań nad wyszukiwaniem ścieżek dla robota powstał zmodyfikowany algorytm Dijkstry, nazwany A1.
A1 nie był optymalnym algorytmem dla robota, ze względu na długi czas pracy.
A2 był algorytmem wykorzystującym heurystykę pozwalająca na ocenienie odległości do mety
Po udowodnieniu optymalności algorytmu A2 zmieniono jego nazwę na A*
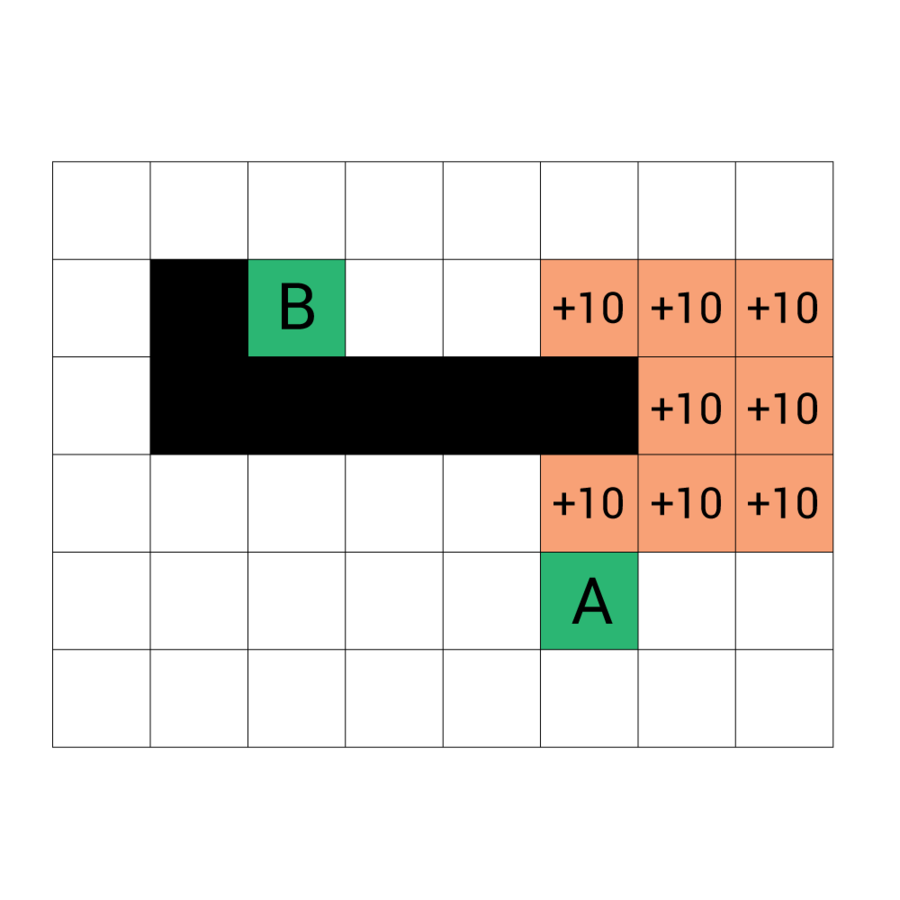
Zmienny koszt ruchu
Więcej niż dwa stany ("Można przejść", "Nie można przejść)
Koszt ruchu może wpłynąć na znalezioną najkrótszą ścieżkę
"Influence mapping" - dynamiczna mapa kosztów
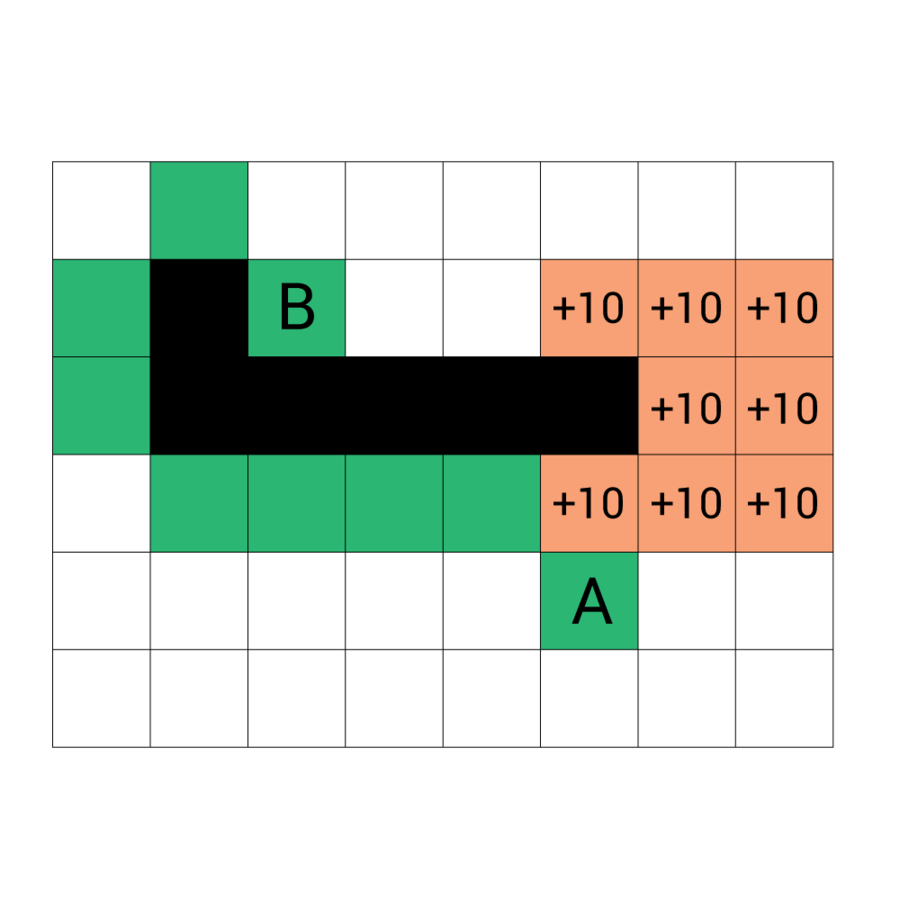
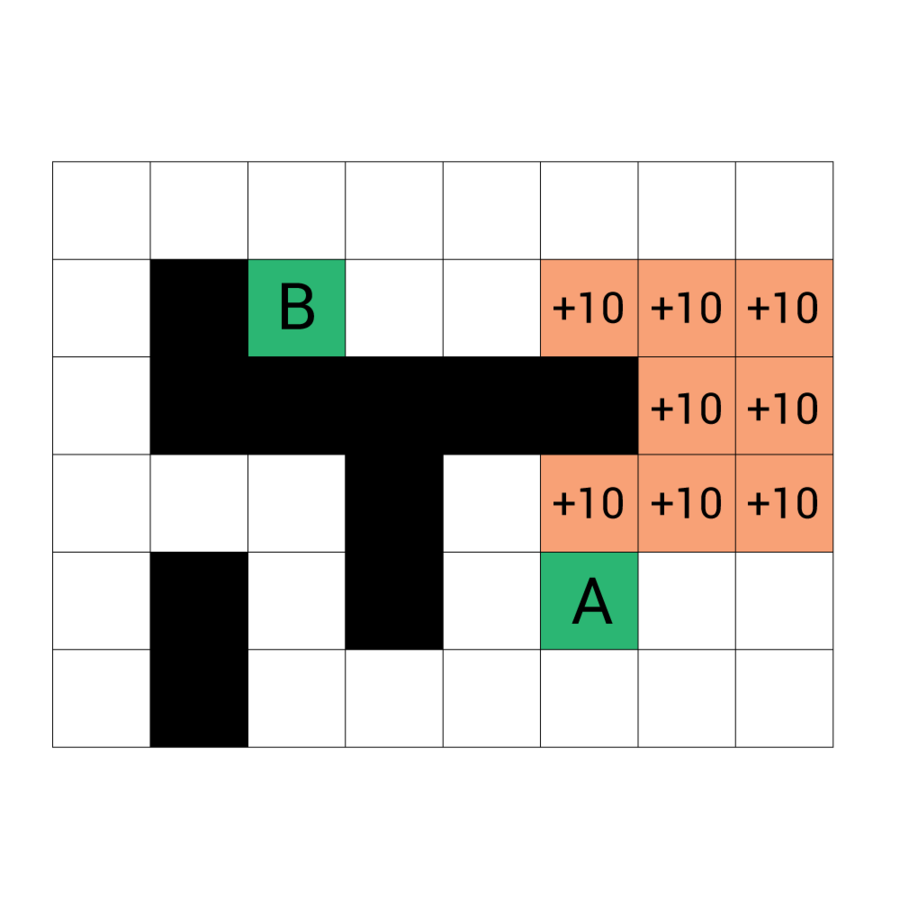
Przestrzeń poszukiwania z polami niekwadratowymi
Możliwość użycia pól o dowolnym kształcie
Należy przechowywać informacje o sąsiedztwie
G uzależniamy od przejścia z jednej krainy do drugiej
H możemy wyliczyć jako odległość w linii prostej
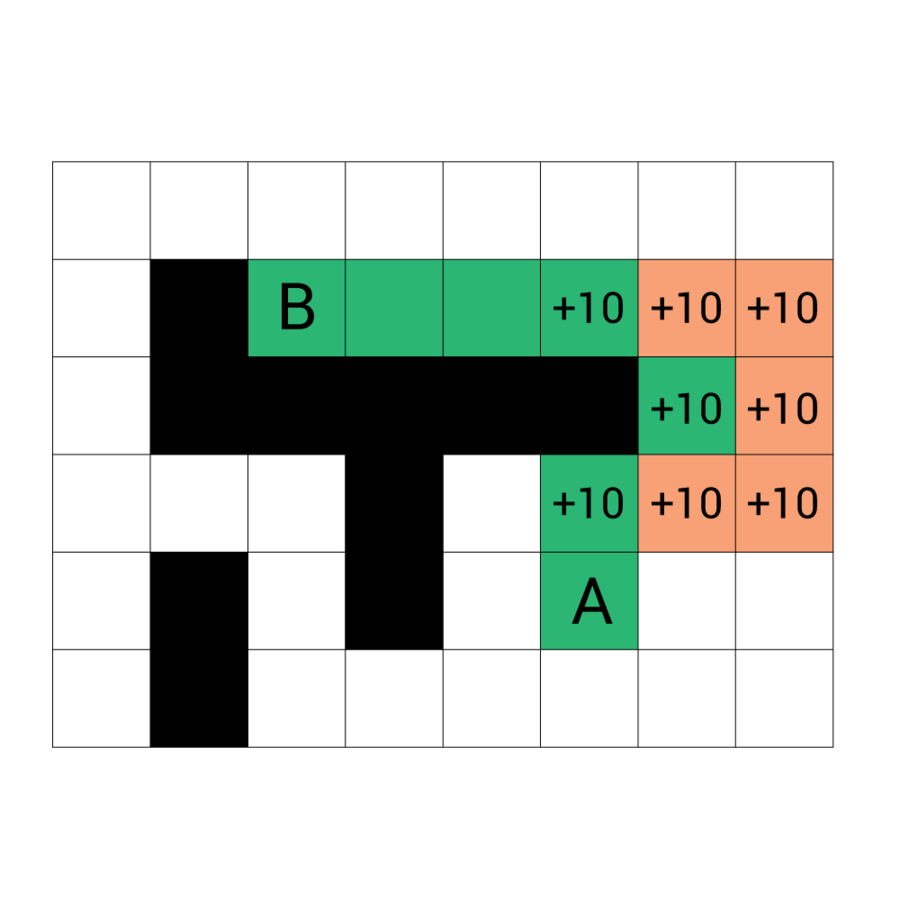
Przestrzeń poszukiwania z polami niekwadratowymi
Zoptymalizowana przestrzeń poszukiwań
Ucinanie ślepych zaułków
Ucinanie miejsc niedostępnych
Większe i mniejsze pola
Zastosowania
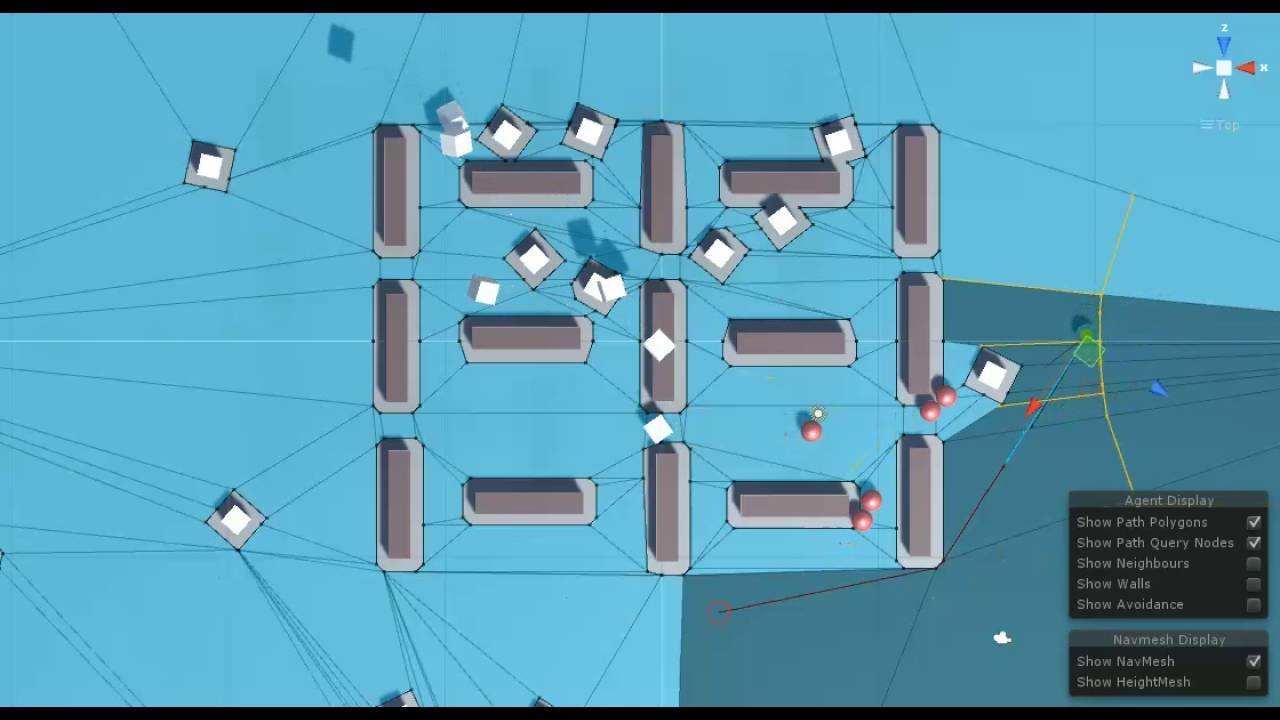
Planowanie ścieżek robotów
i...

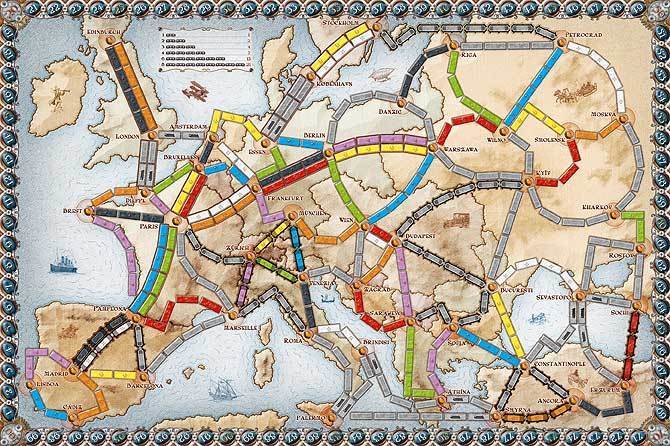
Aplikacje do poszukiwania najkrótszych połączeń kolejowych pomiędzy miastami

Zastosowania
Gry wideo...
Zastosowanie,
Modyfikacje Algorytmu A*
Modyfikacje Algorytmu A*
A*Range



Dziękuję za uwagę