Wprowadzenie do wyszukiwania ścieżek w grafach
Graf
jest strukturą danych składającą się z dwóch zbiorów: zbioru wierzchołków i zbioru krawędzi
Rząd grafu
Rozmiar grafu
to liczba wierzchołków w grafie.
to liczba krawędzi w grafie.
Wierzchołki grafu przechowują informację, natomiast krawędzie określają sposób poruszania się po grafie: z wierzchołka u można przejść do wierzchołka v tylko wtedy, gdy istnieje ścieżka (ciąg krawędzi), która prowadzi w grafie od wierzchołka u do v.
Wybrane pojęcia dotyczące grafów
Graf Prosty
to graf nie posiadający pętli oraz krawędzi podwójnych
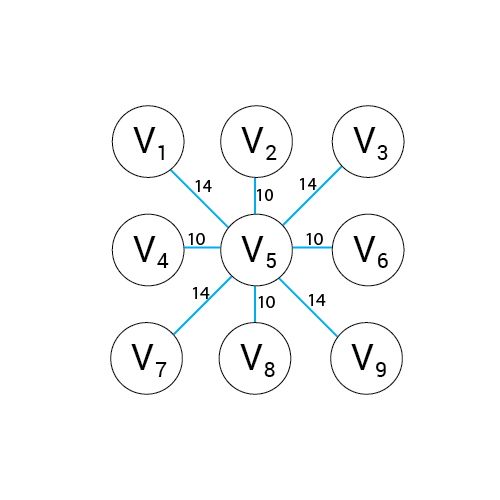
Graf ważony
Stopień Wierzchołka
to graf, który na krawędziach ma dodatkowe wartości nazywane wagami
to liczba krawędzi, które łączą się z danym wierzchołkiem. Jeśli graf posiada pętle, to liczymy je za 2
ścieżka
jest uporządkowanym ciągiem kolejnych krawędzi, po których należy przejść, aby dotrzeć z wierzchołka startowego do wierzchołka końcowego. W grafie może istnieć wiele różnych ścieżek pomiędzy dwoma wybranymi wierzchołkami.
Wybrane pojęcia dotyczące grafów
Przykład
Wybrane pojęcia dotyczące grafów
Przykład
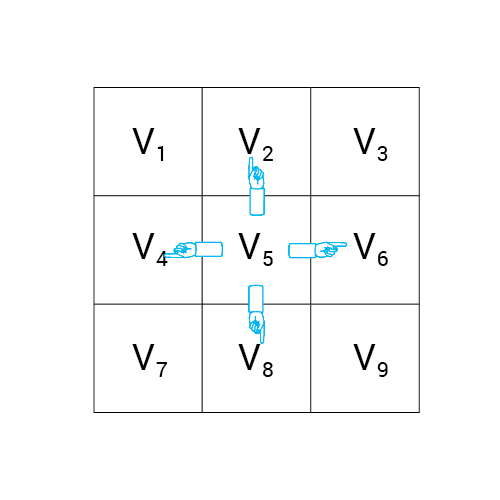
G = (V, E)
V = { v1,v2,v3,v4,v5 }
E = { e1,e2,e3,e4,e5,e6 }
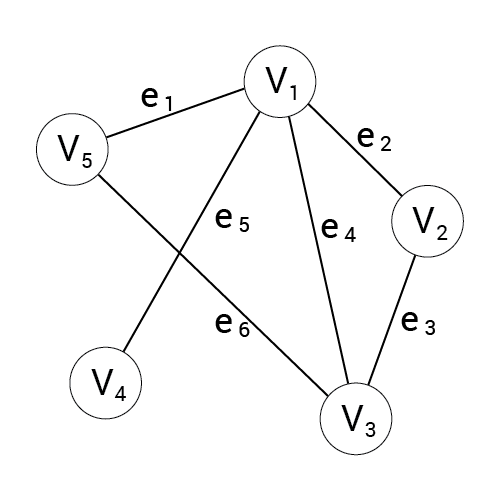
e1 = (v1,v5)
e2 = (v1,v2)
e3 = (v2,v3)
e4 = (v1,v3)
e5 = (v1,v4)
e6 = (v3,v5)
deg(v1) = 4
deg(v2) = 2
deg(v3) = 3
deg(v4) = 1
deg(v5) = 2
P(v3,v5) = { e3, e2, e1 }
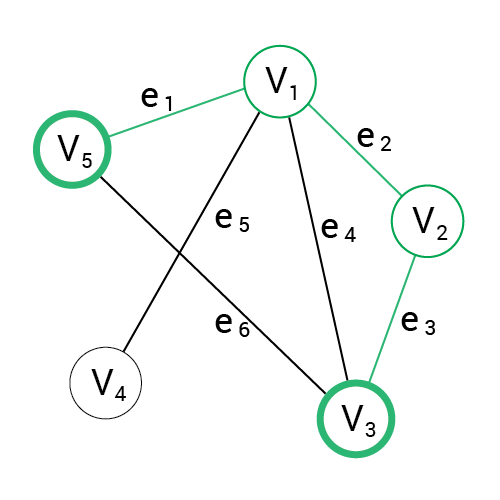
|V| = 5
|E| = 6
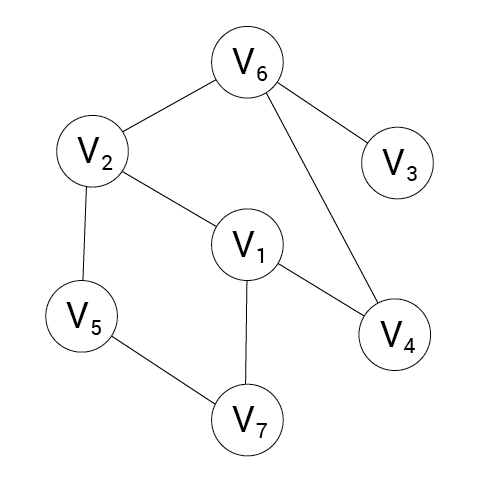
Algorytm DFS
Zaznaczamy bieżący wierzchołek jako odwiedzony. Przechodzimy do kolejnych sąsiadów wierzchołka bieżącego i wykonujemy dla nich tą samą operację (tzn. zaznaczamy je jako odwiedzone i przechodzimy do ich sąsiadów). Przechodzenie kończymy, gdy zostaną w ten sposób odwiedzone wszystkie dostępne wierzchołki.
Przeszukiwanie grafu lub inaczej przechodzenie grafu to czynność polegająca na odwiedzeniu w jakiś usystematyzowany sposób wszystkich wierzchołków grafu w celu zebrania potrzebnych informacji.
Zasada działania przeszukiwania w głąb
Algorytm DFS
Wynik:
stos:
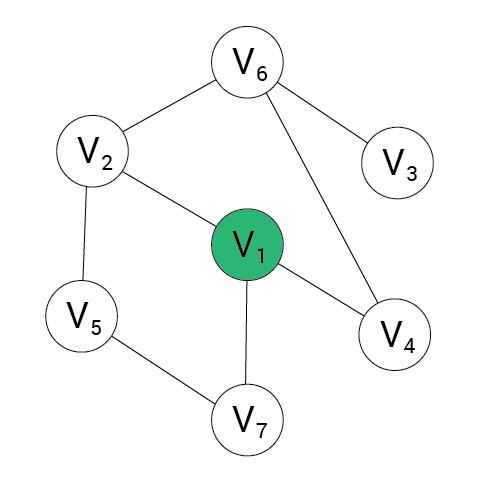
Algorytm DFS
Wynik:
stos:
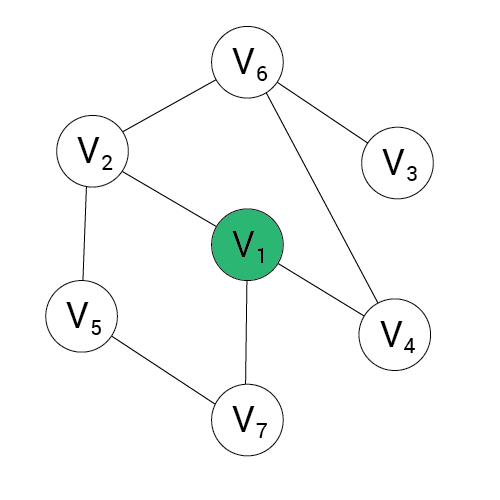
1
1
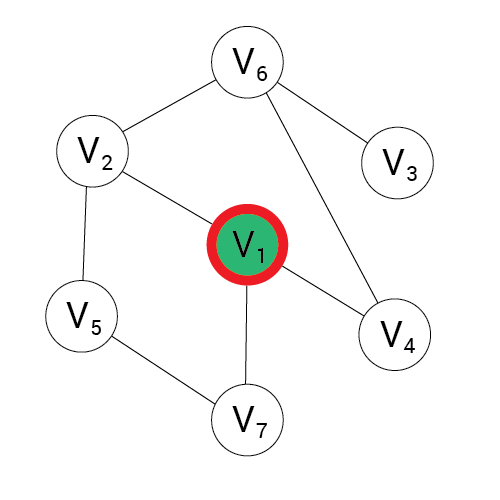
Algorytm DFS
Wynik:
stos:
1, 2
1, 2
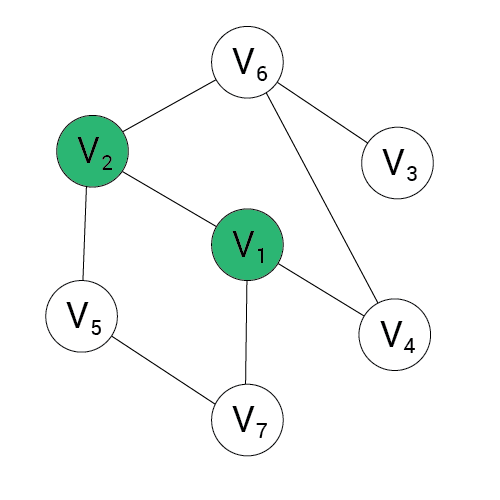
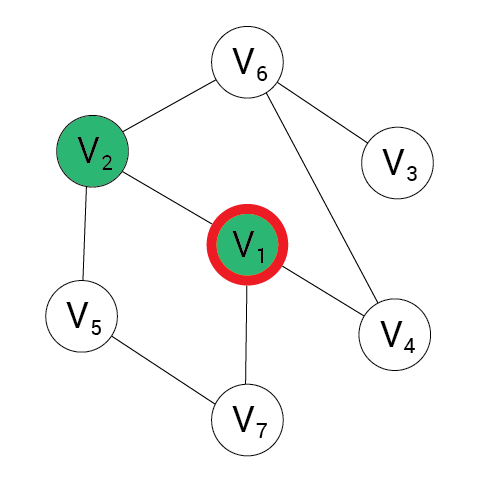
Algorytm DFS
Wynik:
stos:
1, 2, 5
1, 2, 5
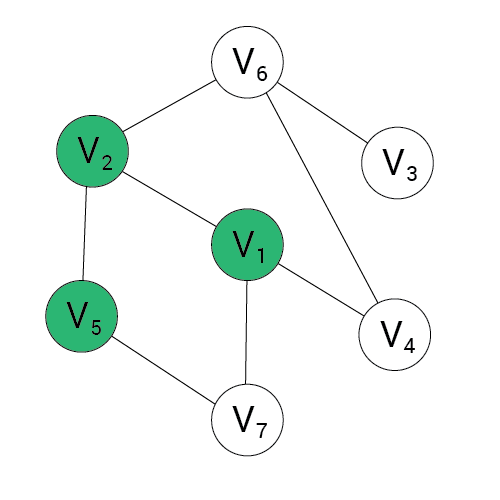
Algorytm DFS
Wynik:
stos:
1, 2, 5, 7
1, 2, 5, 7
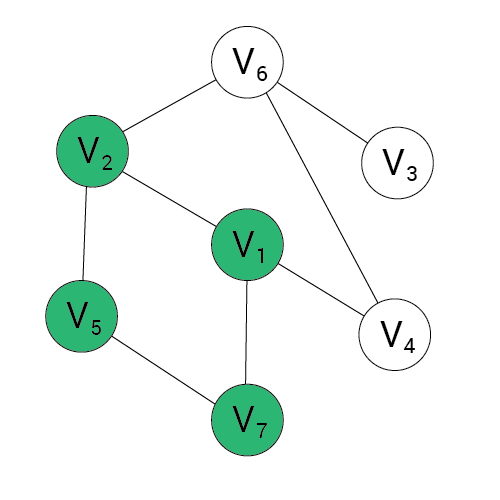
Algorytm DFS
Wynik:
stos:
1, 2, 5, 7
1, 2, 5

Algorytm DFS
Wynik:
stos:
1, 2, 5, 7
1, 2

Algorytm DFS
Wynik:
stos:
1, 2, 5, 7, 6
1, 2, 6
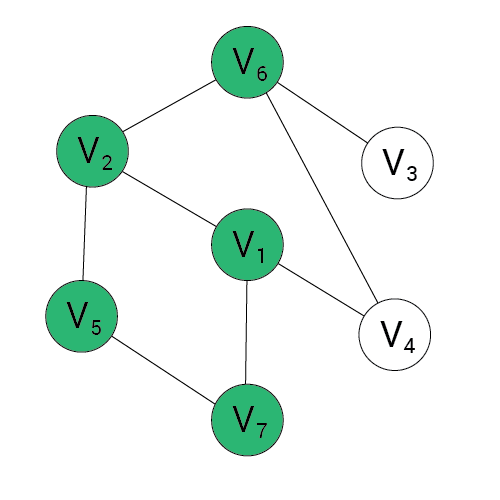
Algorytm DFS
Wynik:
stos:
1, 2, 5, 7, 6, 3
1, 2, 6, 3
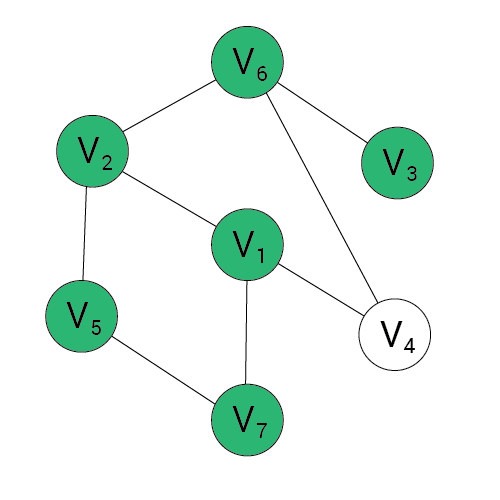
Algorytm DFS
Wynik:
stos:
1, 2, 5, 7, 6, 3
1, 2, 6,

Algorytm DFS
Wynik:
stos:
1, 2, 5, 7, 6, 3, 4
1, 2, 6, 4
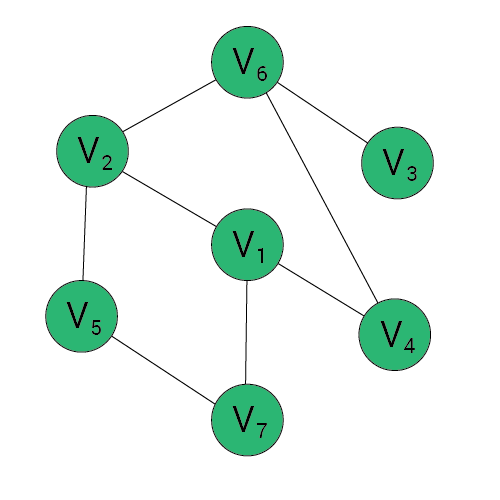
Algorytm DFS
Wynik:
stos:
1, 2, 5, 7, 6, 3, 4
1, 2, 6

Algorytm DFS
Wynik:
stos:
1, 2, 5, 7, 6, 3, 4
1, 2

Algorytm DFS
Wynik:
stos:
1, 2, 5, 7, 6, 3, 4
1

Algorytm DFS
Wynik:
1, 2, 5, 7, 6, 3, 4

Algorytm BFS
Zasada działania przeszukiwania w głąb
Zaczynamy odwiedzanie od wierzchołka startowego. Następnie odwiedzamy wszystkich jego sąsiadów. Dalej odwiedzamy wszystkich nieodwiedzonych jeszcze sąsiadów sąsiadów. Itd.
Algorytm DFS
Wynik:
Kolejka:
Algorytm BFS
Wynik:
Kolejka:
1
Algorytm BFS
Wynik:
Kolejka:
1
Algorytm BFS
Wynik:
Kolejka:
1, 2
2
Algorytm BFS
Wynik:
Kolejka:
1, 2, 4
2, 4
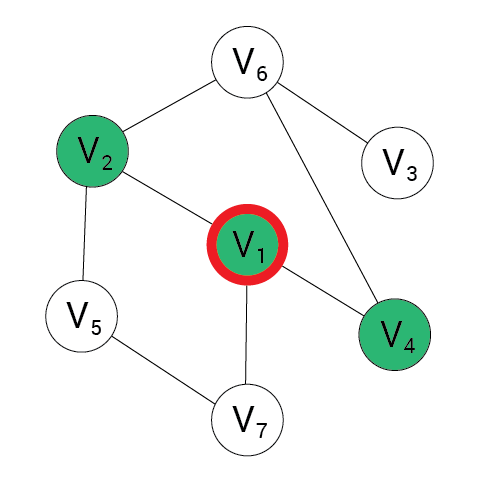
Algorytm BFS
Wynik:
Kolejka:
1, 2, 4, 7
2, 4, 7
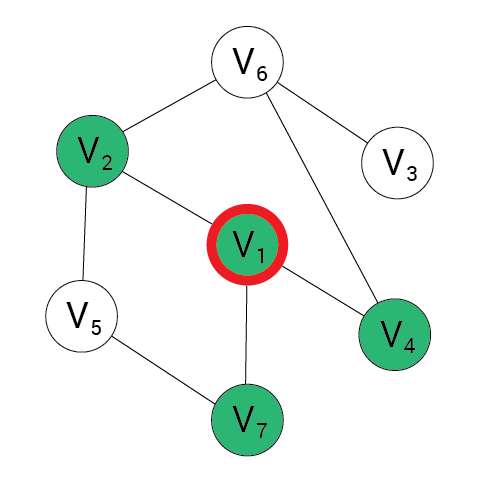
Algorytm BFS
Wynik:
Kolejka:
1, 2, 4, 7
4, 7
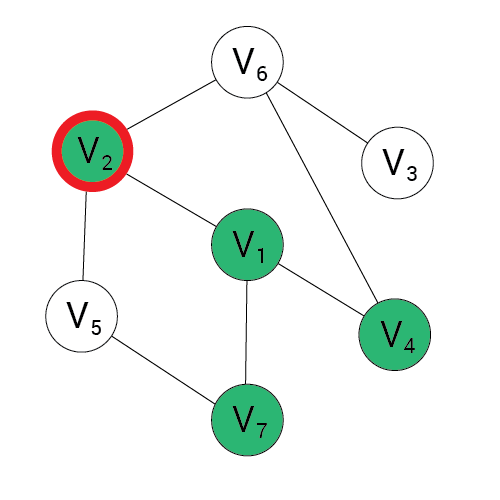
Algorytm BFS
Wynik:
Kolejka:
1, 2, 4, 7, 5
4, 7, 5
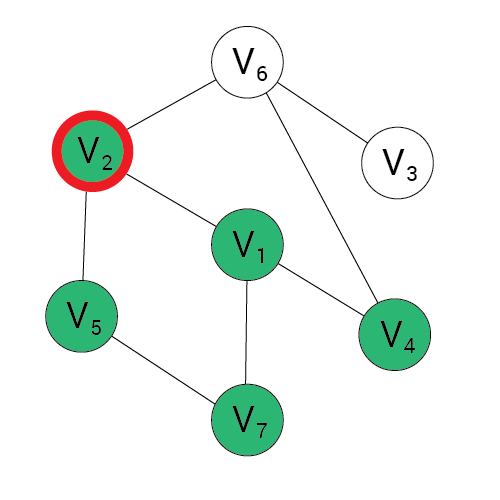
Algorytm BFS
Wynik:
Kolejka:
1, 2, 4, 7, 5, 6
4, 7, 5, 6
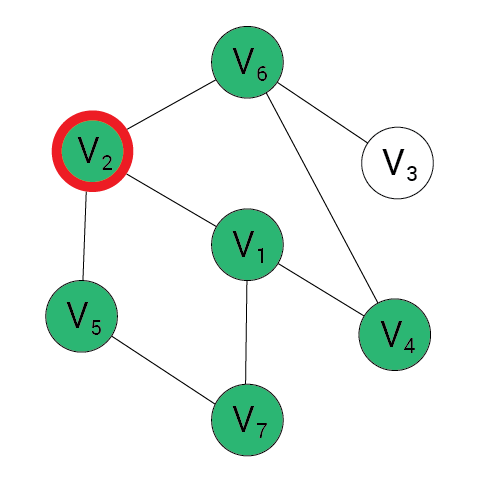
Algorytm BFS
Wynik:
Kolejka:
1, 2, 4, 7, 5, 6
7, 5, 6
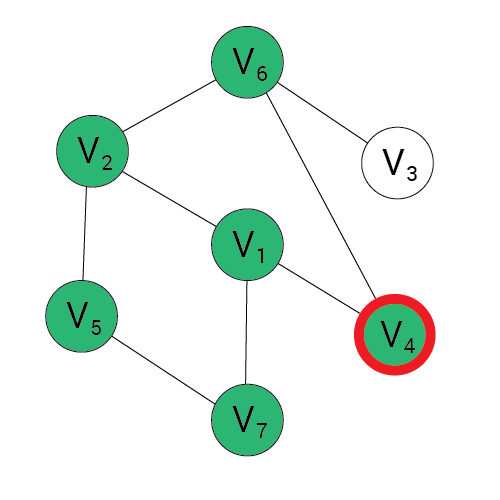
Algorytm BFS
Wynik:
Kolejka:
1, 2, 4, 7, 5, 6
5, 6
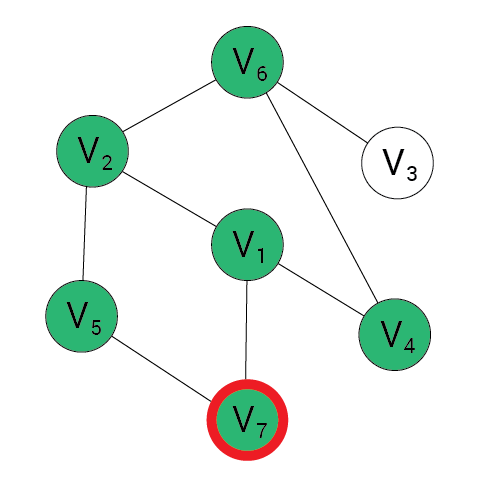
Algorytm BFS
Wynik:
Kolejka:
1, 2, 4, 7, 5, 6
6
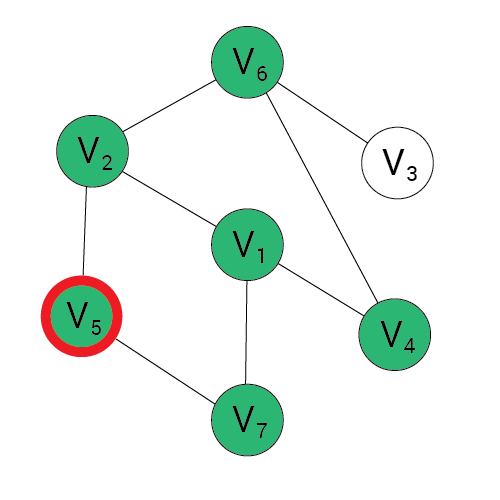
Algorytm BFS
Wynik:
Kolejka:
1, 2, 4, 7, 5, 6
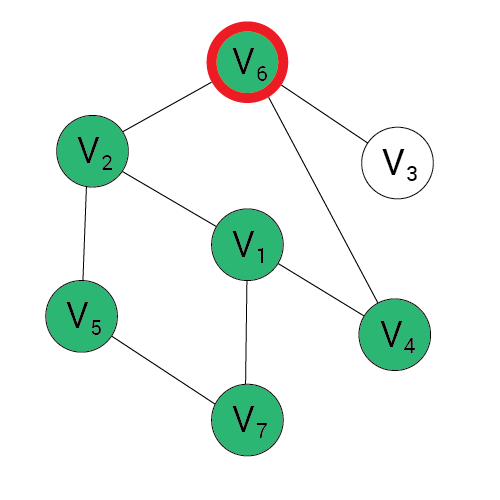
Algorytm BFS
Wynik:
Kolejka:
1, 2, 4, 7, 5, 6, 3
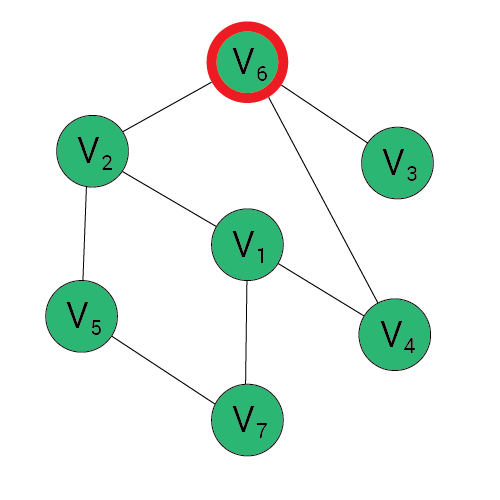
3
Algorytm BFS
Wynik:
Kolejka:
1, 2, 4, 7, 5, 6, 3
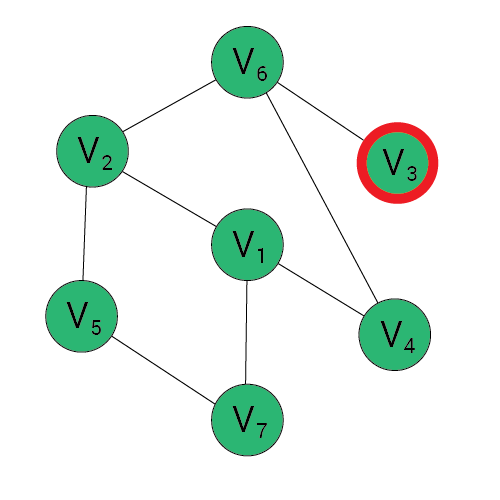
Algorytm BFS
Wynik:
1, 2, 4, 7, 5, 6, 3
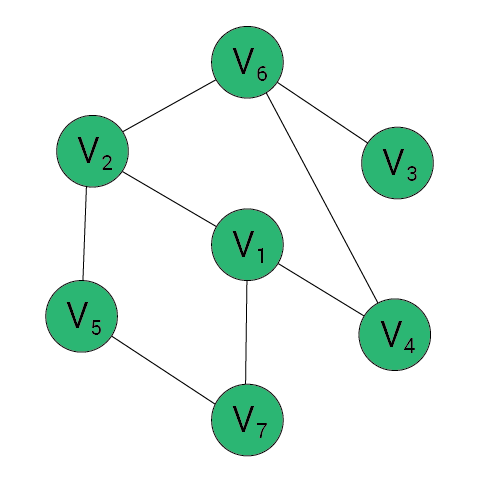
Złożoność czasowa
W najgorszym przypadku przeszukiwania wszerz i w głąb muszą przebyć wszystkie krawędzie prowadzące do wszystkich węzłów, złożoność czasowa wynosi O(|V| + |E|), gdzie |V| to liczba węzłów, a |E| to liczba krawędzi w grafie.
Złożoność Pamięciowa
Złożoność pamięciowa przeszukiwania w głąb w przypadku drzewa jest o wiele mniejsza niż przeszukiwania wszerz, gdyż algorytm w każdym momencie wymaga zapamiętania tylko ścieżki od korzenia do bieżącego węzła, podczas gdy przeszukiwanie wszerz wymaga zapamiętywania wszystkich węzłów w danej odległości od korzenia, co zwykle rośnie wykładniczo w funkcji długości ścieżki.
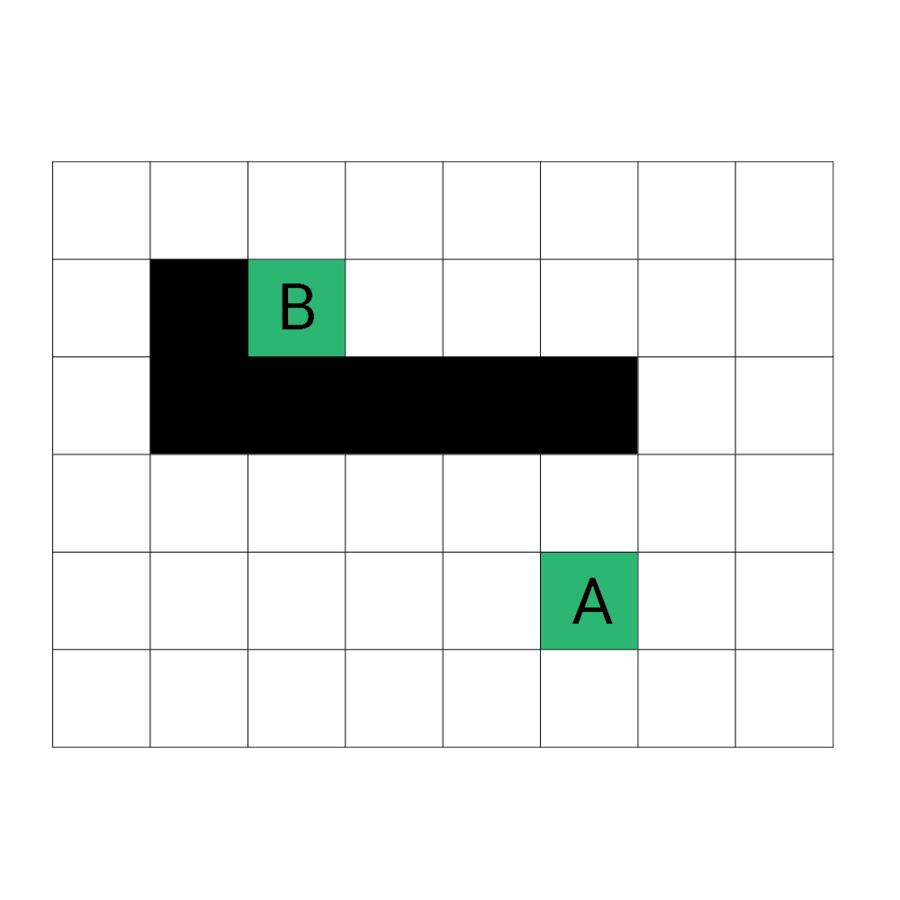
Algorytm a*
algorytm heurystyczny znajdowania najkrótszej ścieżki w grafie ważonym z dowolnego wierzchołka do wierzchołka spełniającego określony warunek zwany testem celu.
Algorytm a*
Algorytm A* od wierzchołka początkowego tworzy ścieżkę, za każdym razem wybierając wierzchołek x z dostępnych w danym kroku niezbadanych wierzchołków tak, by minimalizować funkcję f(x) zdefiniowaną:
f(x) = g(x) + h(x)
gdzie:
g(x) to droga pomiędzy wierzchołkiem początkowym a x. Dokładniej: suma wag krawędzi, które należą już do ścieżki plus waga krawędzi łączącej aktualny węzeł z x.
f(x) przewidywana przez heurystykę droga od x do wierzchołka docelowego.
W każdym kroku algorytm dołącza do ścieżki wierzchołek o najniższym współczynniku f. Kończy w momencie natrafienia na wierzchołek będący wierzchołkiem docelowym.
Algorytm a*
Algorytm a*

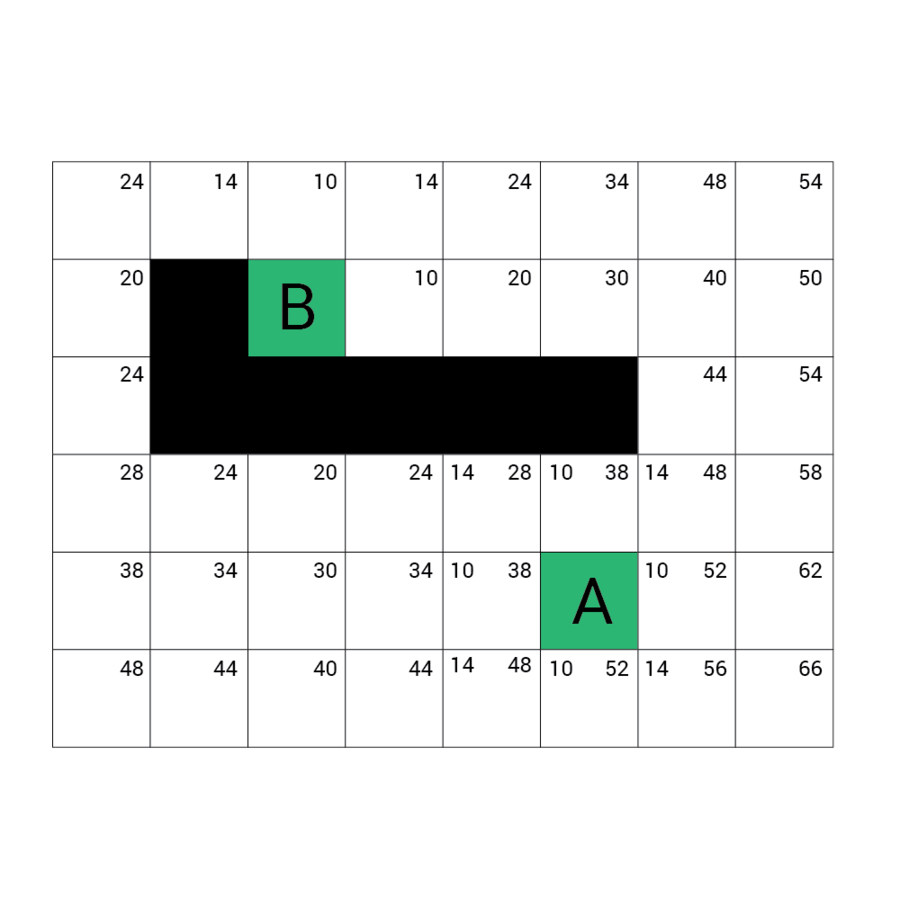
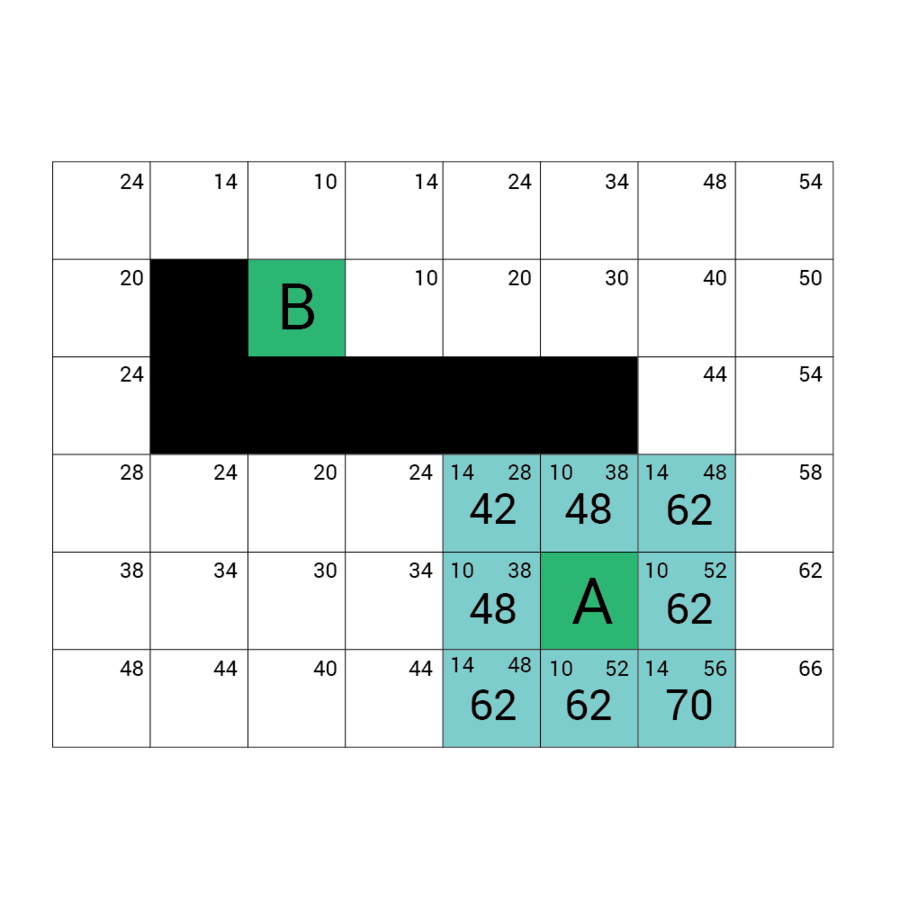
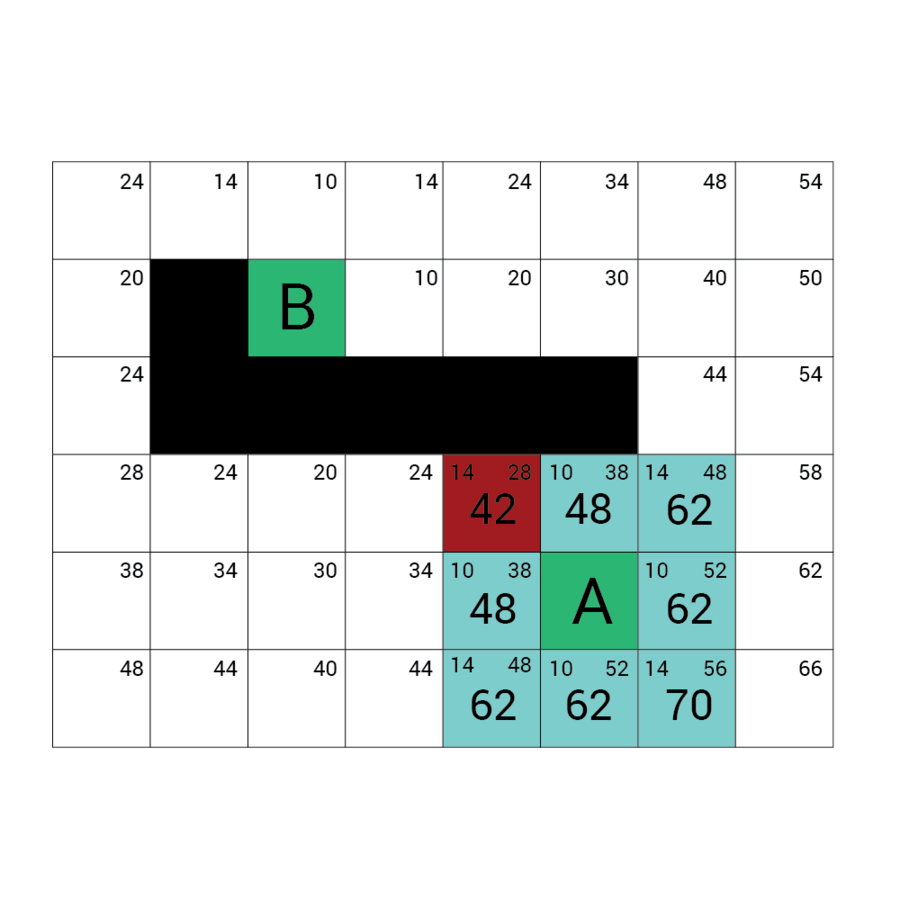
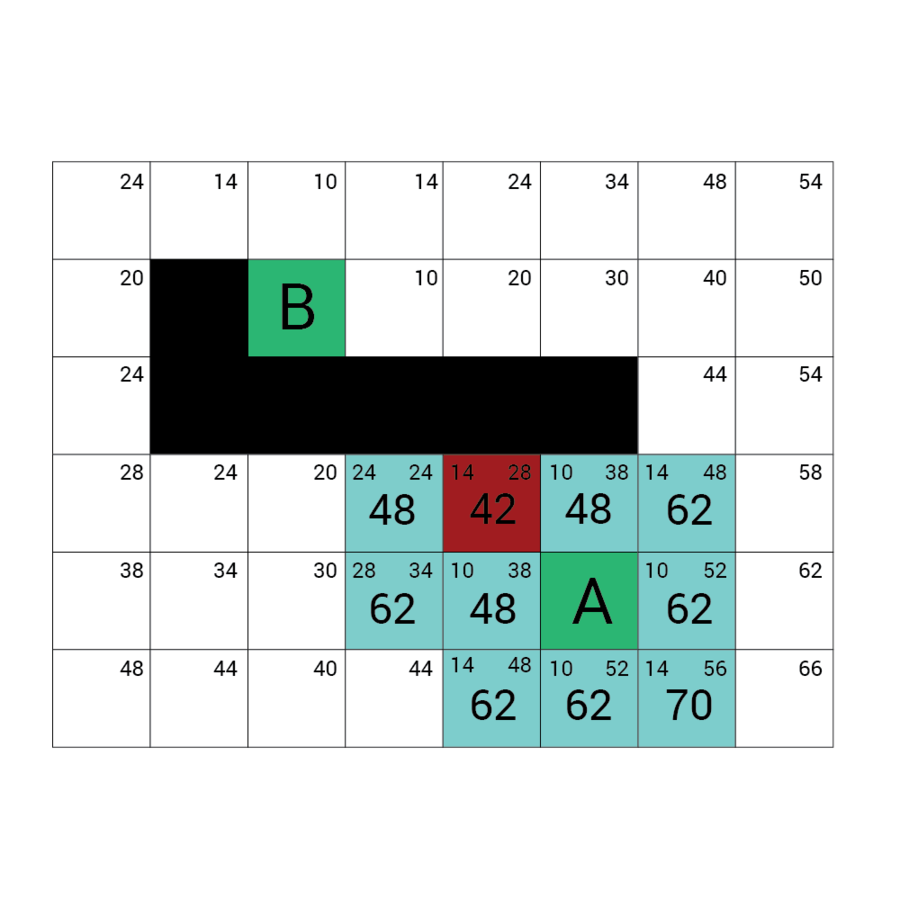
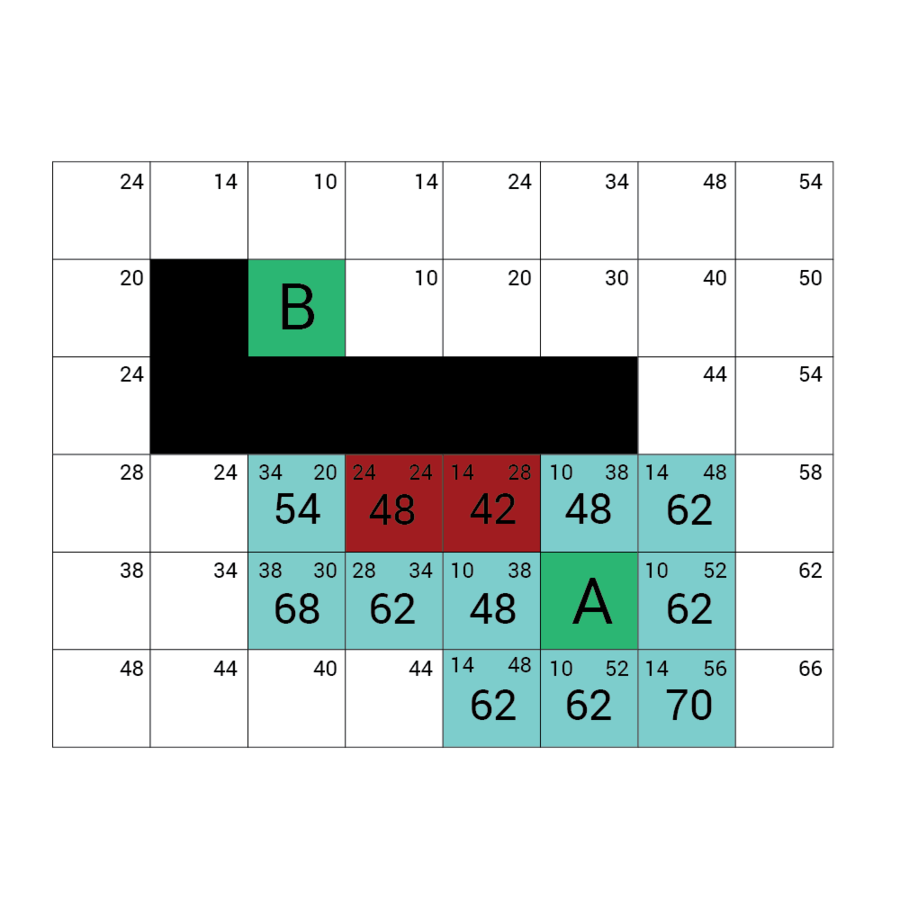
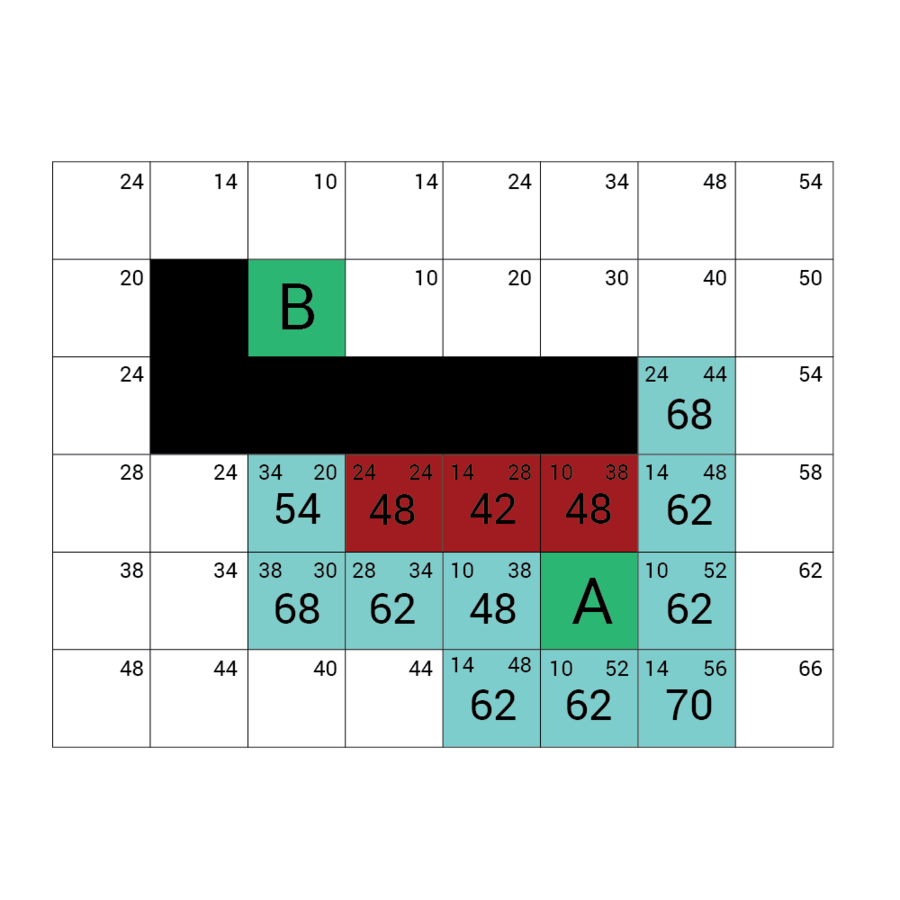
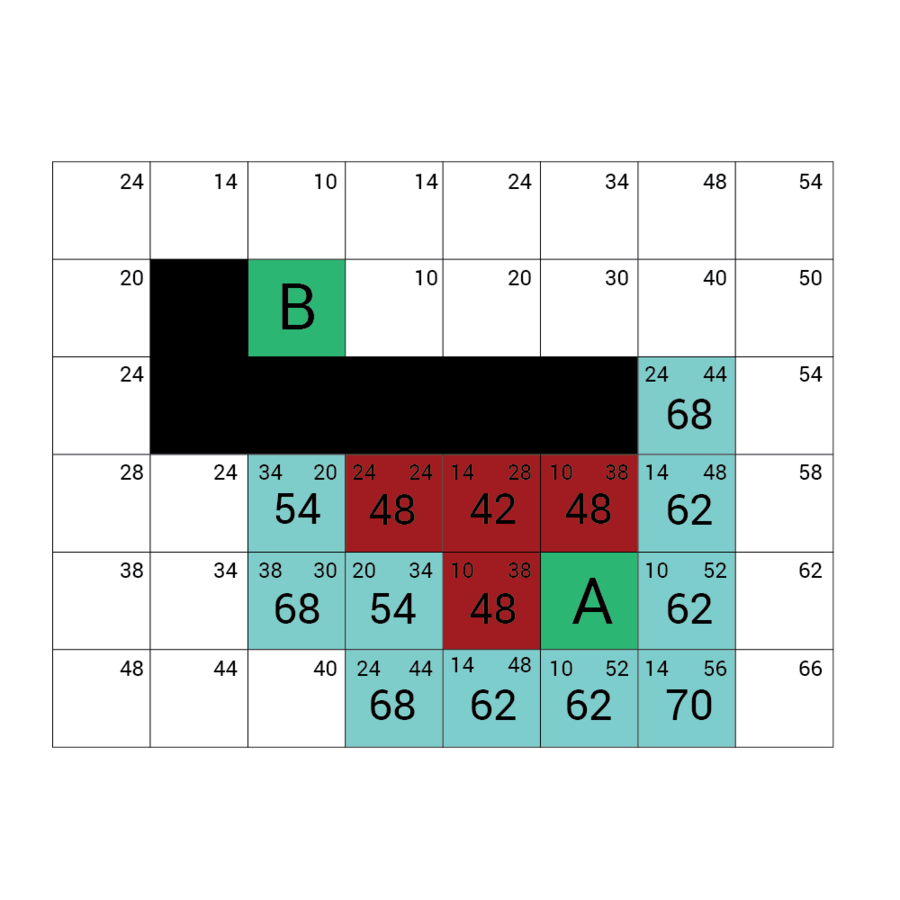
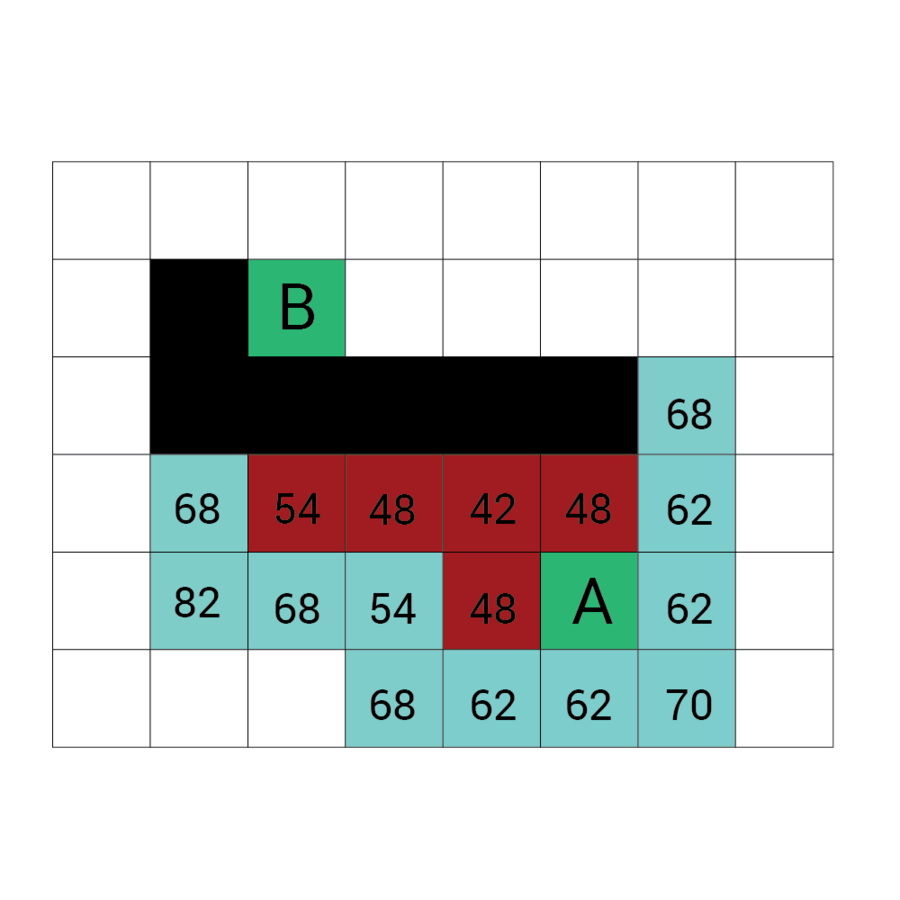
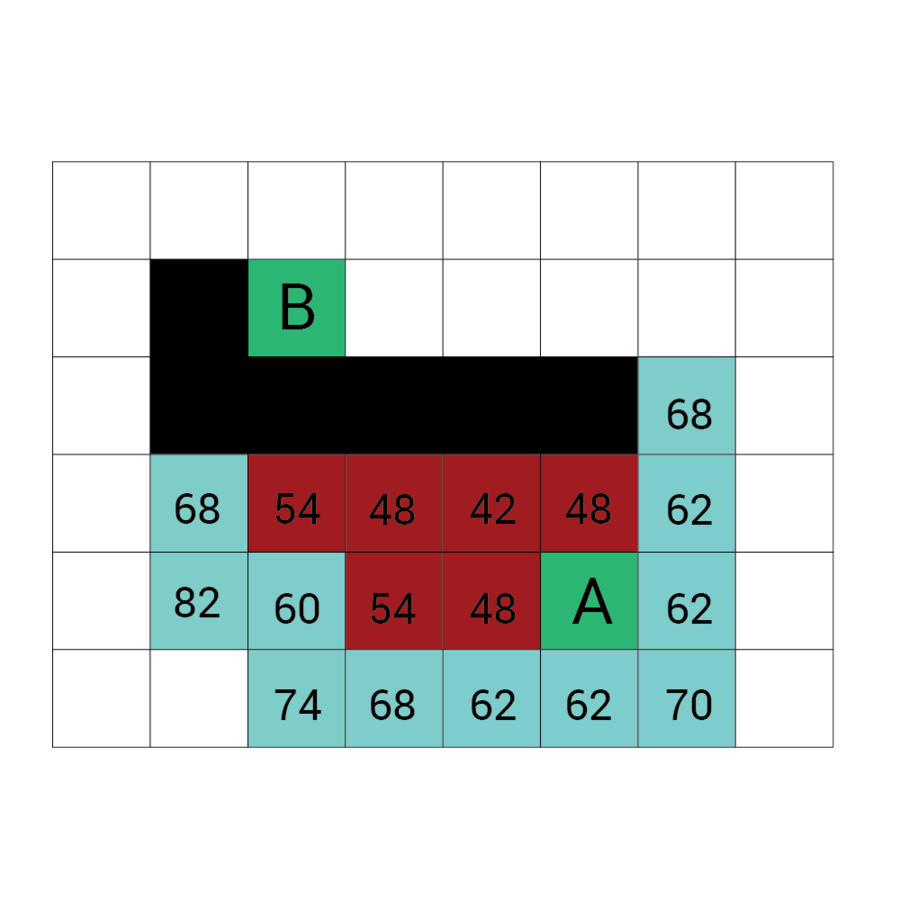
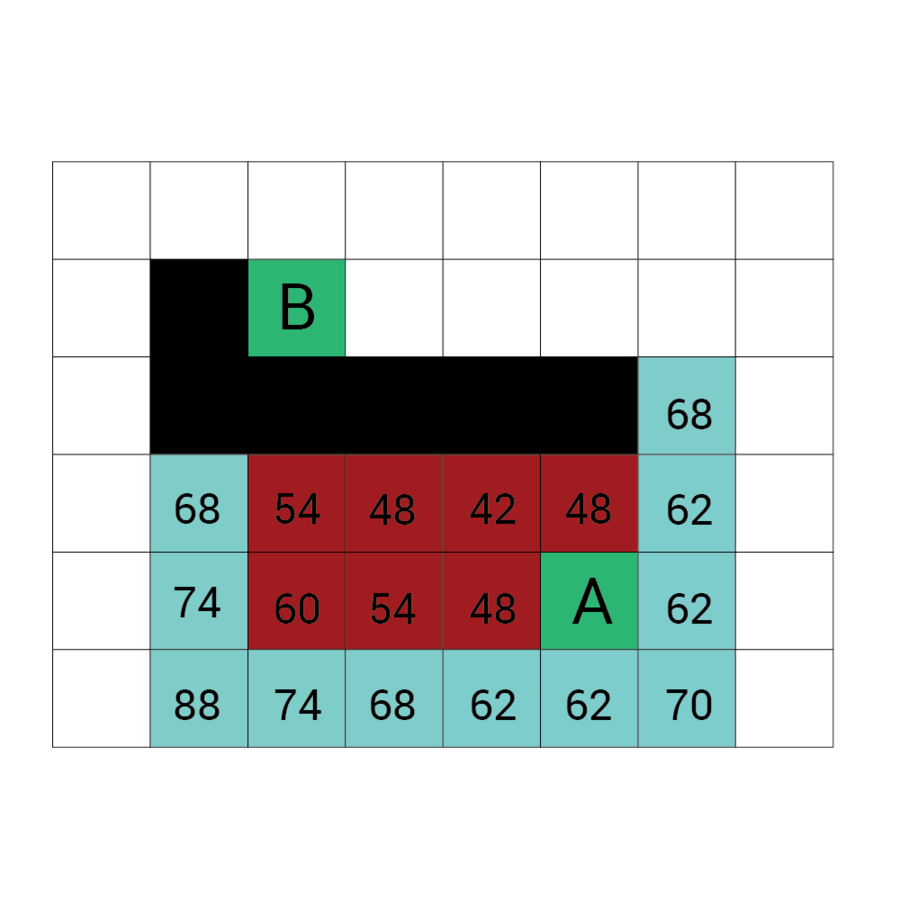
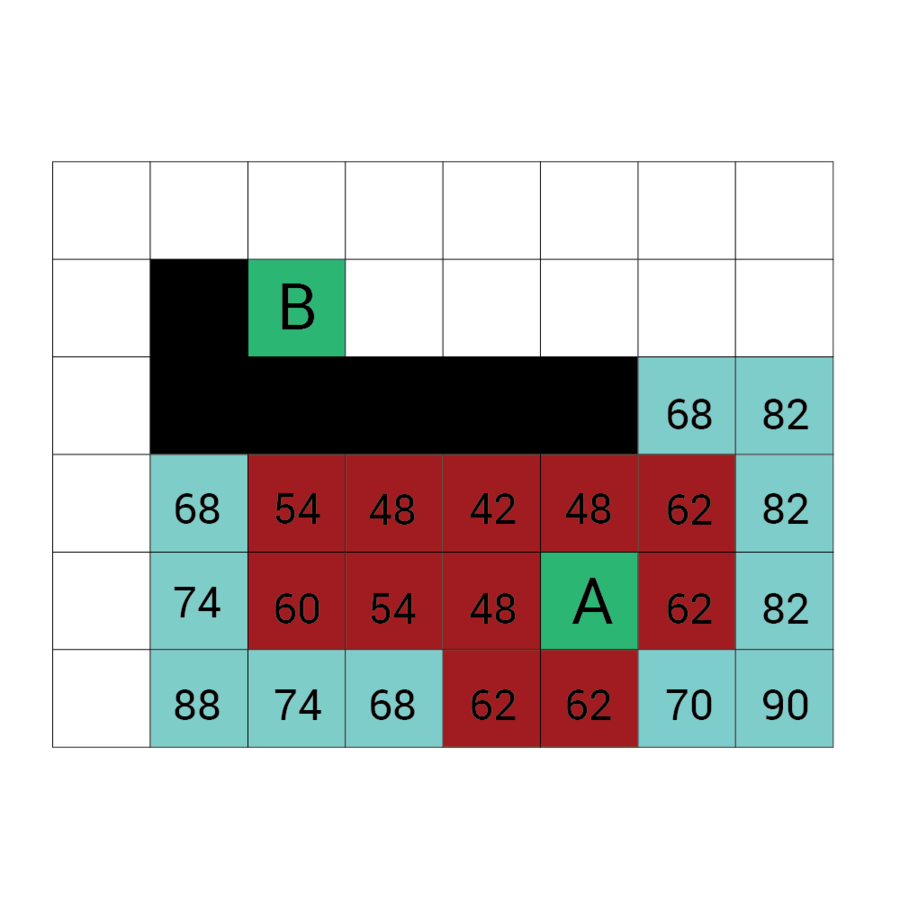
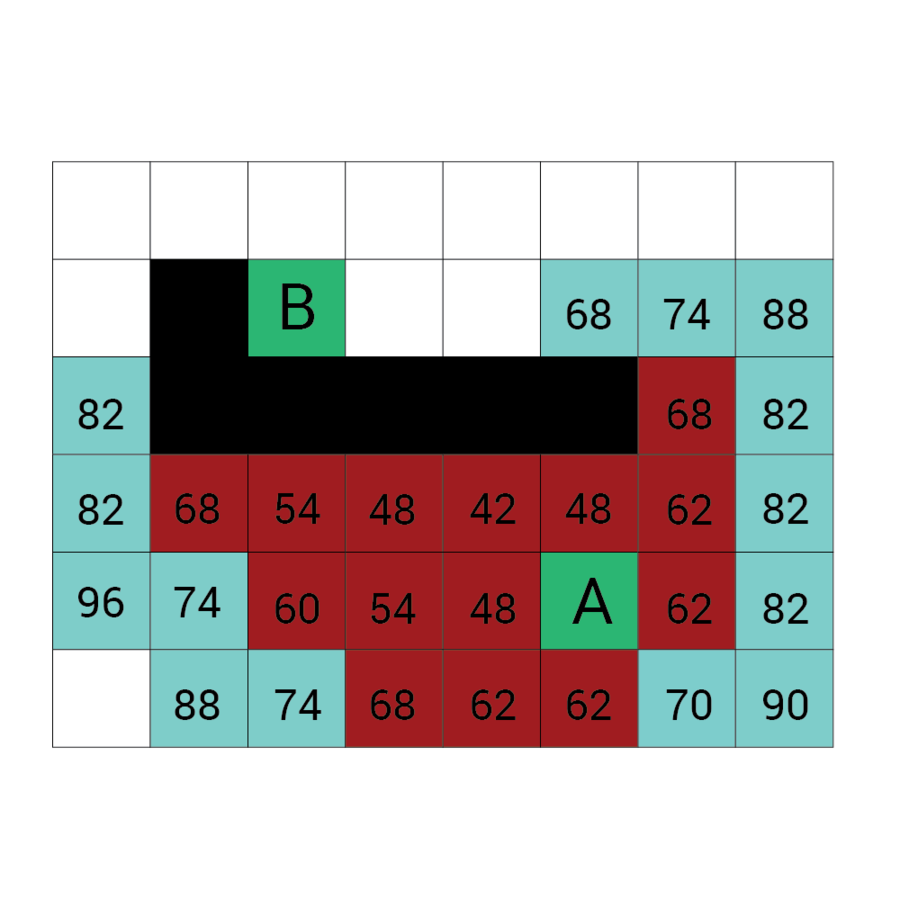
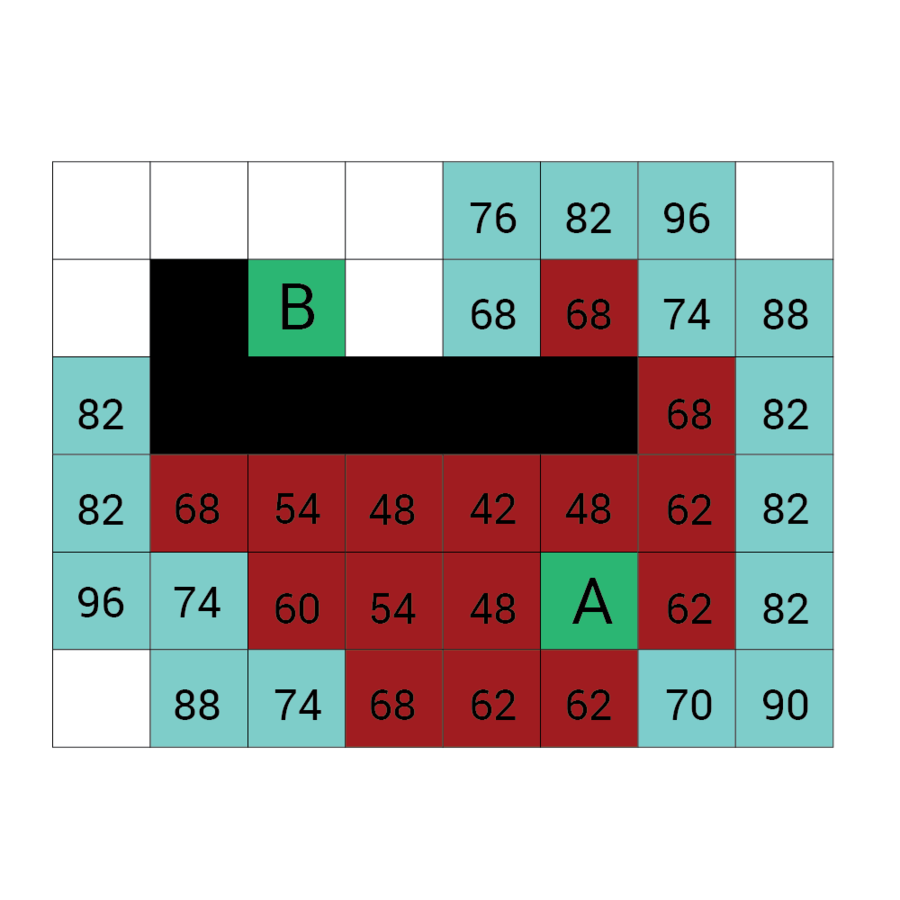
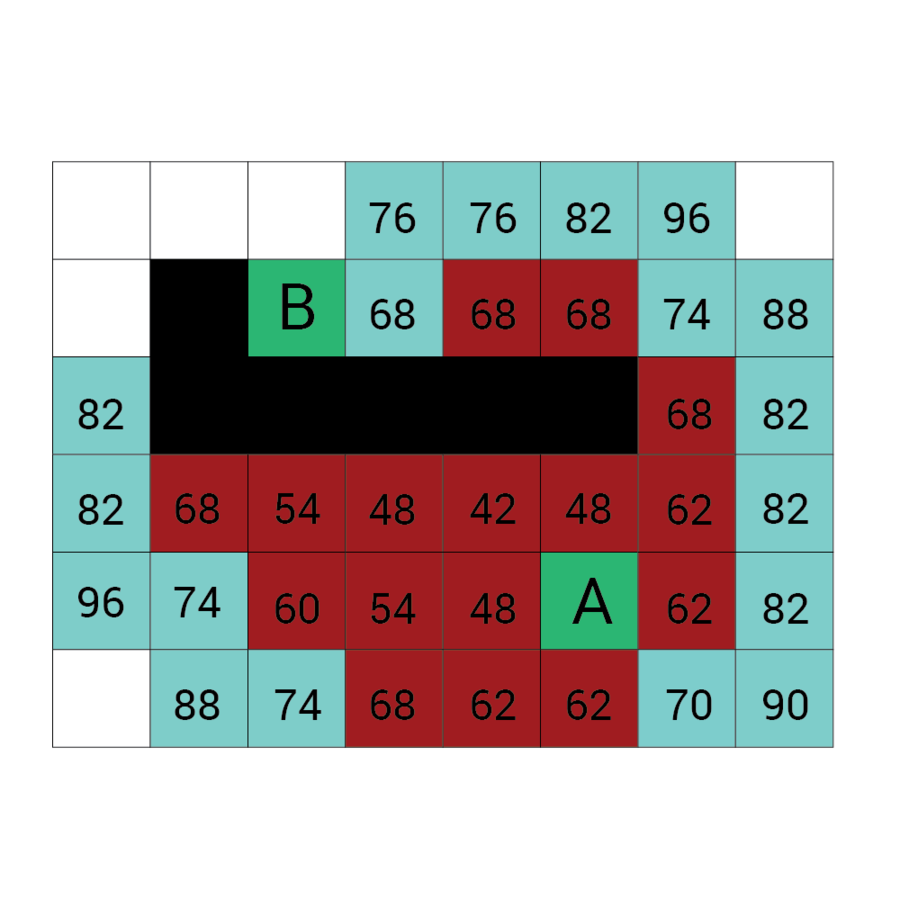
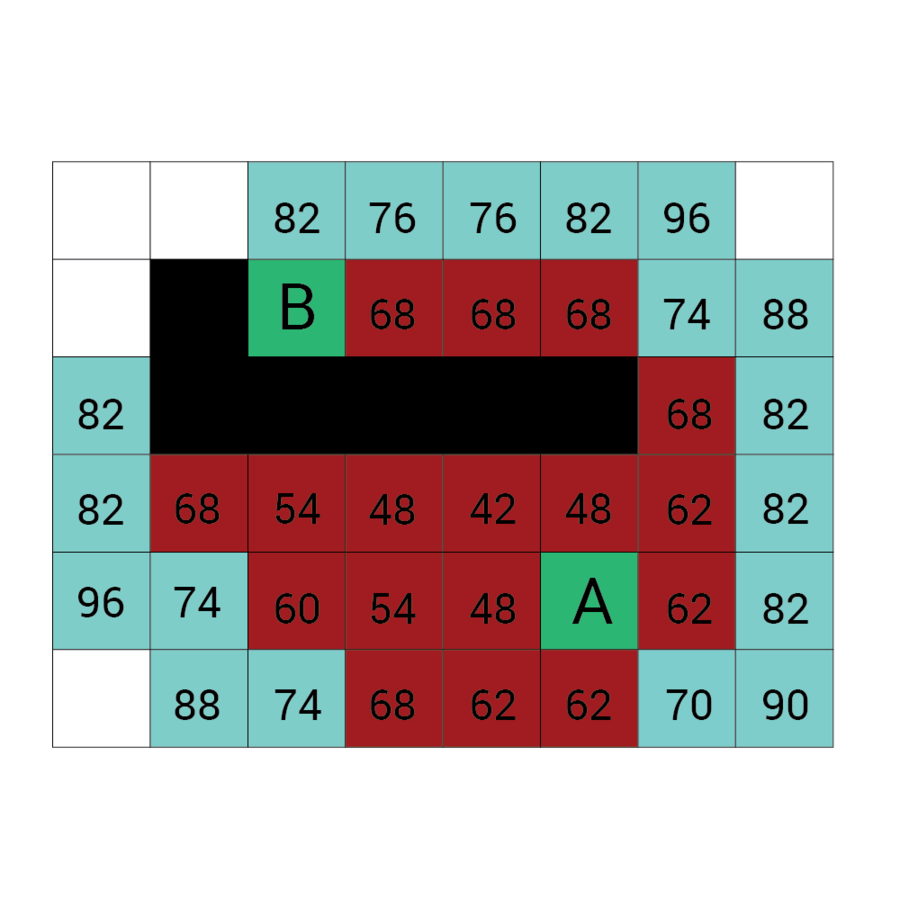
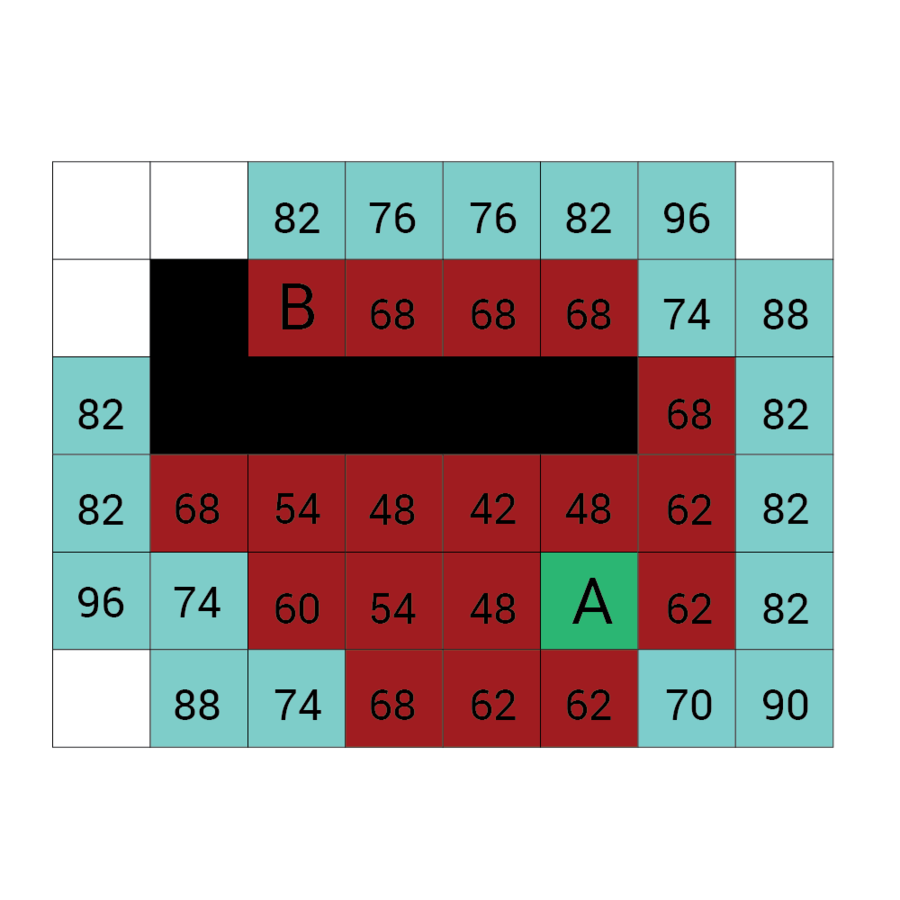
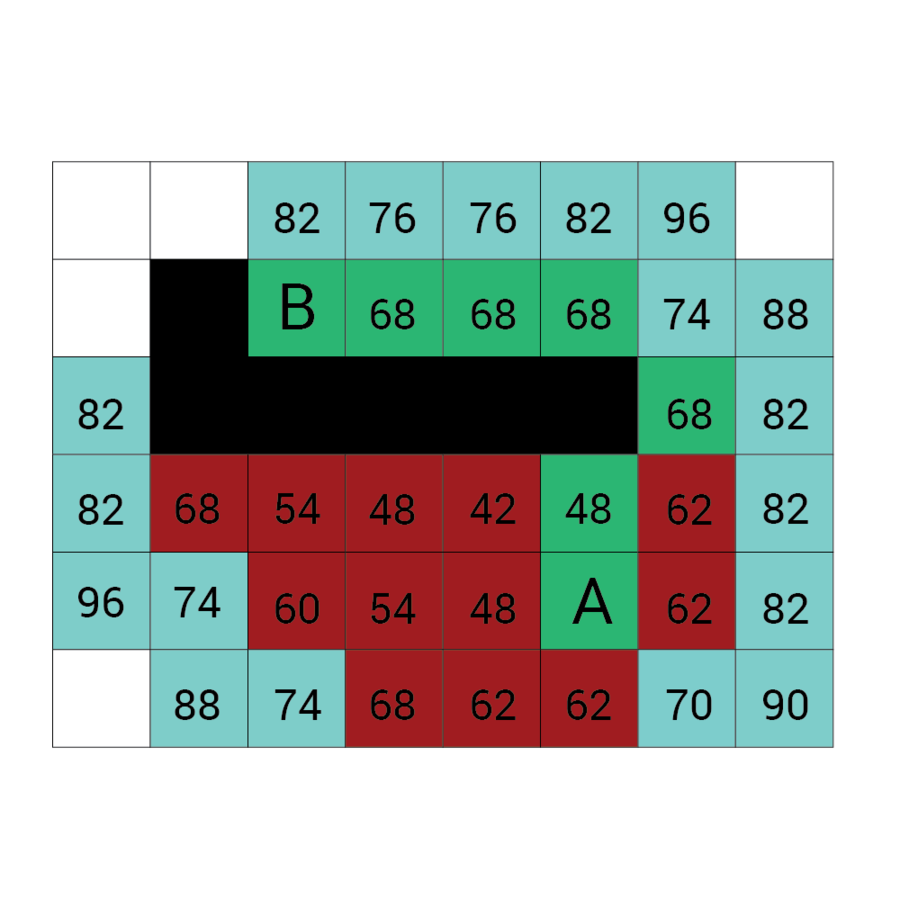
Wartość h
Wartość f
Wartość G
wartość H + wartość G
Odległość z A
Odległość z B
Algorytm a*
Przykłady
źródło: https://sebastian.itch.io/
Algorytm a*
Przykłady
źródło: https://sebastian.itch.io/
Algorytm a*
Przykłady
źródło: https://sebastian.itch.io/