Pigeonhole Principle

Simple Idea 💡

Suppose you are given 5 Pigeons and 4 pigeonholes, and you start putting pigeons one by one into each pigeonhole.

|p| |p| |p| |p| |p|

Simple Idea 💡

Suppose you are given 5 Pigeons and 4 pigeonholes, and you start putting pigeons one by one into each pigeonhole.

|p| |p| |p| |p| |p|

then you will have one pigeon left, and you can put it into any of the pigeonholes.

|pp| |p| |p| |p|

Conclude: When number of pigeons > number of pigeonholes, there will be at-least one pigeonhole with at least two pigeons.

Hair Counting Example

If the amount of hair is expressed in terms of the number of hair starands, the average human head about 1,50,000 strands of hair.

Assuming no human head has more than 1M strands of hair. Given population of Delhi is 30M, we can conclude then there would be many people who have exactly same amount of hair.

DivSubs

You are given a multiset of N integers. Please find such a nonempty subset of it that the sum of the subset's elements is divisible by N. Otherwise, state that this subset doesn't exist.

-1 if the required subset doesn't exist
If the required subset exists, output two lines. Output the size of the subset on the first line and output the list of indices of the multiset's element that form the required subset. Of course, any number can be taken in the subset no more than once.

1 <= N <= 10^5

Input
4 6 10

Output
1
2

Gray Similar Code

Given N 64 bit integers such that any two successive numbers differ at exactly 1 bit. We have to find out 5 integers such that their XOR is equal to 0.

Output Yes or No.

Input
5
1 0 2 3 7

Output
Yes

Holiday

Summary:

Given a weighted tree, consider there are N people in N Nodes. You have to re-arrage people sucht that everyone is in new node and no node contains more than one person under the constraint that the distance travelled for each person must be maximized. There are N cities having N-1 highways connecting them.

Hints 👨‍💻

All Edges will be used to travel around.

We need to maximize the user of every edge used. Once we know know how many time each is used, we can calculate the answer.

Mathematical Expectation

Expectation = Avg value of a Random Variable!

Mathematically, for a discrete variable X with probability function P(X), the expected value E[X] is given by Σ xiP(xi) the summation runs over all the distinct values xi that the variable can take

For a continuous variable X with probability density function P(x) , the expected value E[X] is given by ∫ xP(x)dx.

Linearity of Expectation

The rule of "linearity of of the expectation" says that

E[x1+x2] = E[x1] + E[x2].

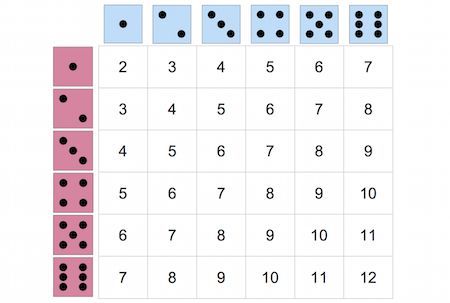
Suppose we are playing a game in which we take the sum of the numbers rolled on two six-sided dice. Calculate the expected value of the sum of the rolls.

Expected Heads

A fair coin is thrown N times, what is the expected number of Heads.

Problems 👀!

What is the expected number of coin flips to get a head?

What is the expected number of coin flips to get two consecutive heads?

What is the expected number of coin flips to get N consecutive heads?

Bernaulli'sTrial

Bernaulli Trial

An experiment is called a bernaulli trial if it has exactly two outcomes, one of which is desired.

For example - flipping a coin, selecting a number from 1 to 100 to get a prime, rolling a dice to get 4 etc. The result of a bernaulli trial can typically be represented as "yes/no" or "success/failure".

Theorem 1

If the probability of success of a bernaulli trial is p then the expected number of trials to get a success is 1/p.

Theorem 2

If probability of getting success in Bernaulli Trial is p, then expected number of successes in n trials in np.

Interview Candidates

Candidates are appearing for interview one after other. Probability of each candidate getting selected is 0.16. What is the expected number of candidates that you will need to interview to make sure that you select somebody?

Choose Number

N students are asked to choose a number from 1 to 100 inclusive. What is the expected number of students that would choose a single digit number?

Coupon Collector 👨‍💻

Coupon Collector Problem

A certain brand distributes a coupon a packet of chips. The coupon is chosen randomly from a set of 'N' distinct coupons. What is the expected number of packets one must buy so that you get all 'n' distinct coupons.