1.7 Sigmoid Neuron

The building block of Deep Neural Networks

Recap: Six jars

What we saw in the previous chapter?

(c) One Fourth Labs

\( \in \mathbb{R} \)

Classification

loss = \sum_i (y_i-\hat{y_i})^2

loss = \sum_i (y_i-\hat{y_i})^2

Accuracy=\frac{\text{Number of correct predictions}}{\text{Total number of predictions}}

Accuracy=\frac{\text{Number of correct predictions}}{\text{Total number of predictions}}

Loss

Model

Data

Task

Evaluation

Learning

Real inputs

Boolean Output

Perceptron Learning Algorithm

Some thoughts on the contest

Just some ramblings!

(c) One Fourth Labs

We should create the binary classification monthly contest such that we can somehow visualize that the data is not linearly separable (don't know how)

We should also be able to visualize why the perceptron model is not fitting

Also give them some insights into what does the loss function indicate and how to make sense of it

Limitations of Perceptron

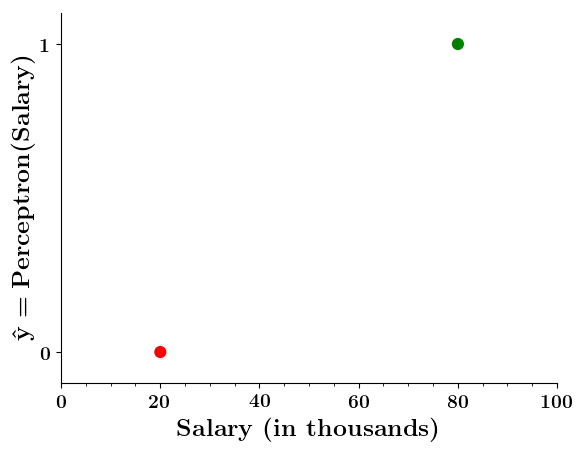
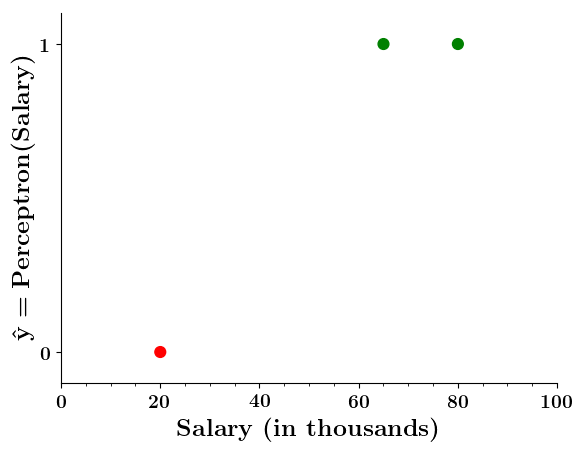
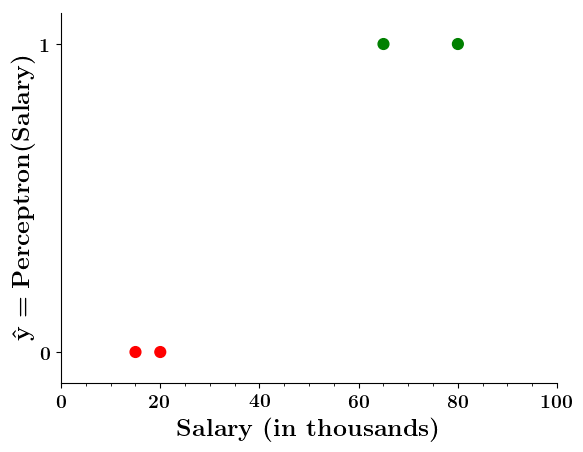
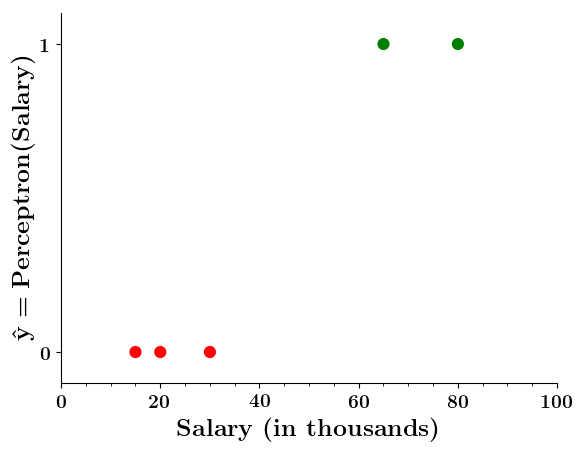
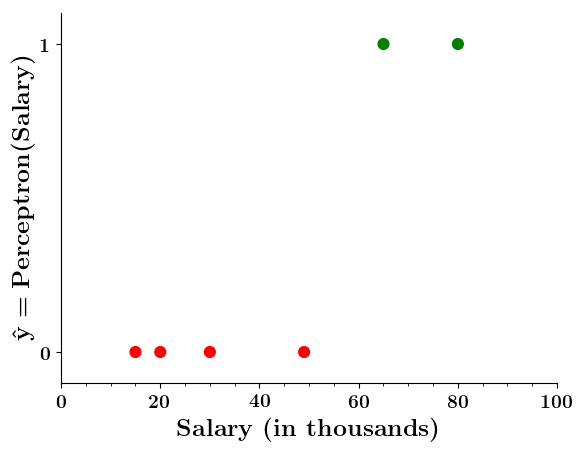
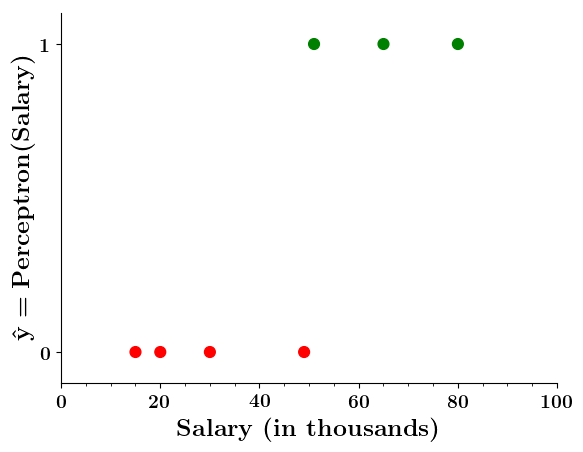
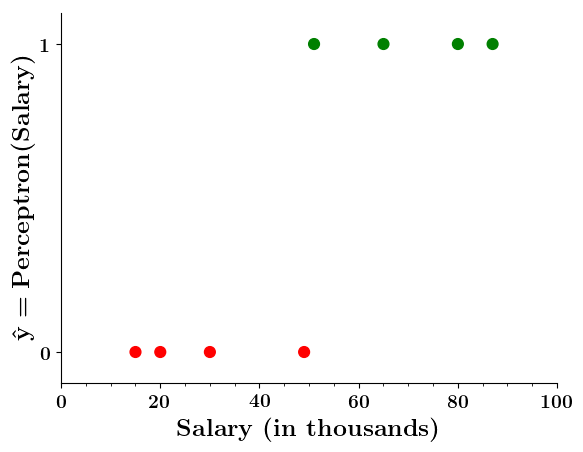
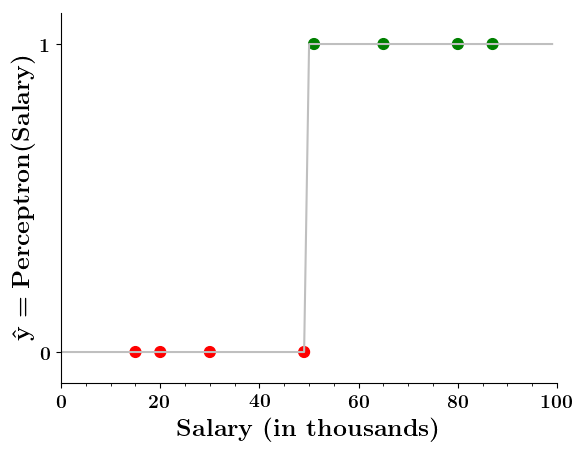
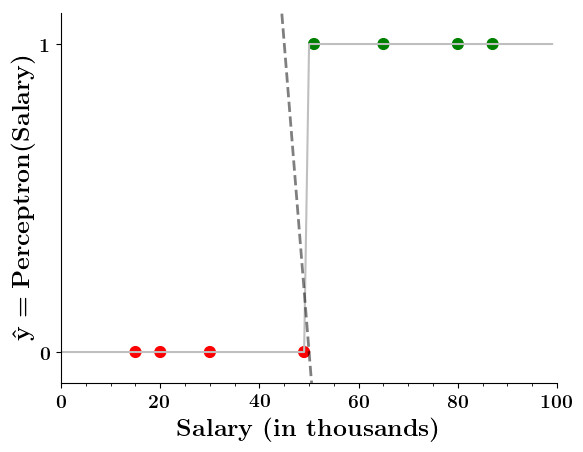
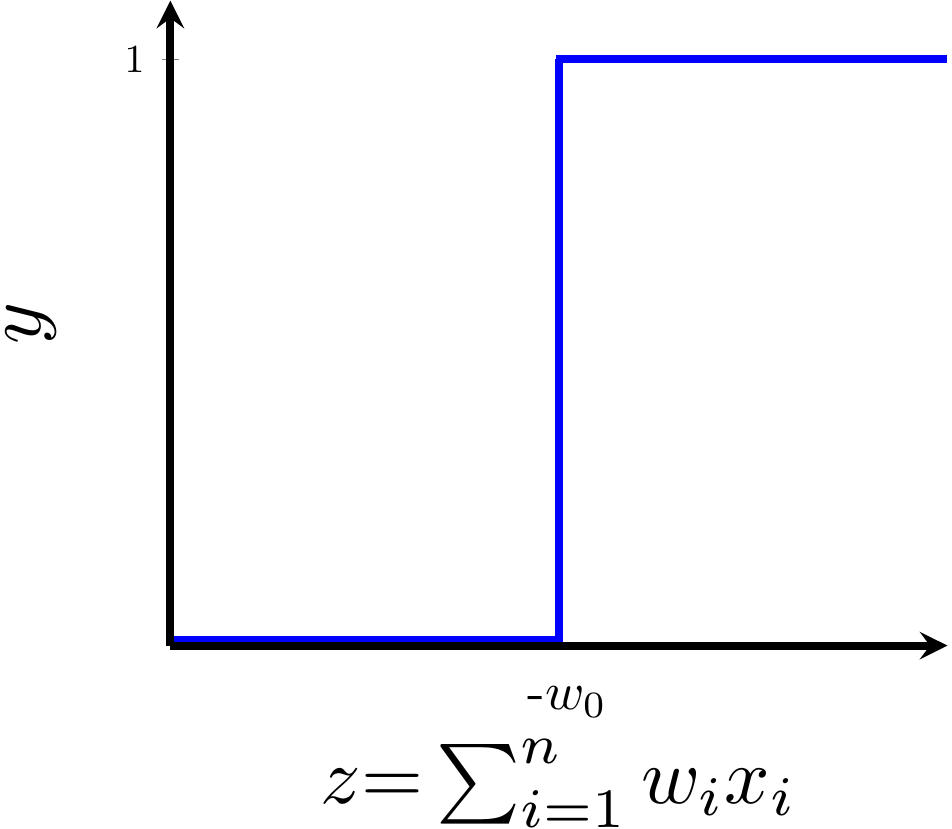
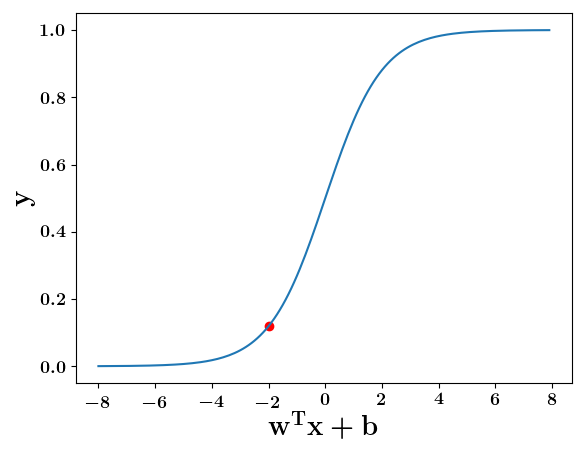
Can we plot the perceptron function ?

(c) One Fourth Labs

Wait a minute!

Salary ( in thousands)	Can buy a car?
80	1
20	0
65	1
15	0
30	0
49	0
51	1
87	1

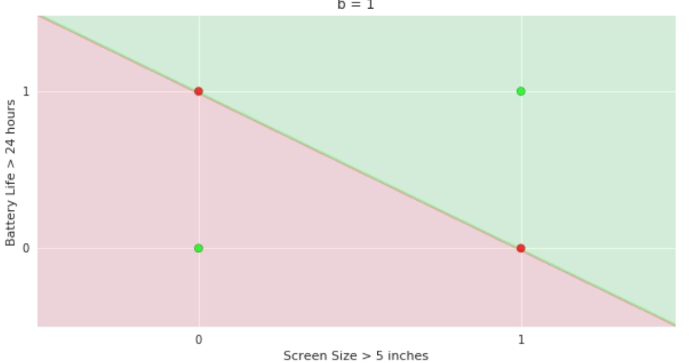
Doesn't the perceptron divide the input space into positive and negative halves ?

y=\sum_{i=1}^n w_i x_i \geq b

y=\sum_{i=1}^n w_i x_i \geq b

\text{Suppose,} \\ \mathbb{w_1} = 0.2,\\ \hspace{-0.1cm}\mathbb{b}\ \ = -10

\text{Suppose,} \\ \mathbb{w_1} = 0.2,\\ \hspace{-0.1cm}\mathbb{b}\ \ = -10

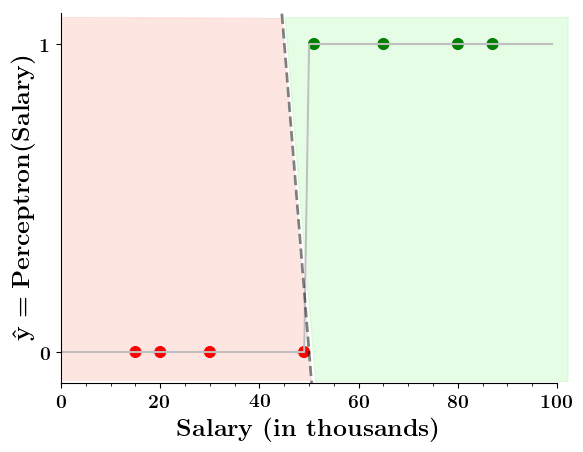
Limitations of Perceptron

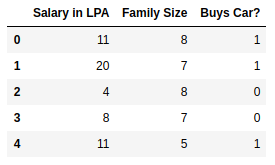
How does the perceptron function look in 2 dimensions?

(c) One Fourth Labs

y=\sum_{i=1}^n w_i x_i \geq b

y=\sum_{i=1}^n w_i x_i \geq b

\text{Suppose,} \\ \mathbb{w_1} = 0.2,\\ \hspace{-0.2cm}\mathbb{w_2} = 0.1 \\ \mathbb{b} = -10.5

\text{Suppose,} \\ \mathbb{w_1} = 0.2,\\ \hspace{-0.2cm}\mathbb{w_2} = 0.1 \\ \mathbb{b} = -10.5

Salary (in thousands)	Family size	Can buy a car?
80	2	1
20	1	0
65	4	1
15	7	0
30	6	0
49	3	0
51	4	1
87	8	1

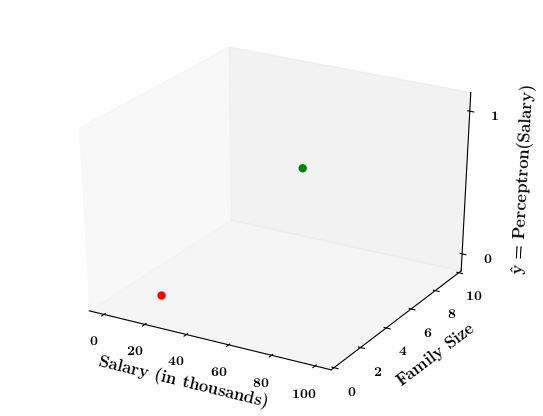
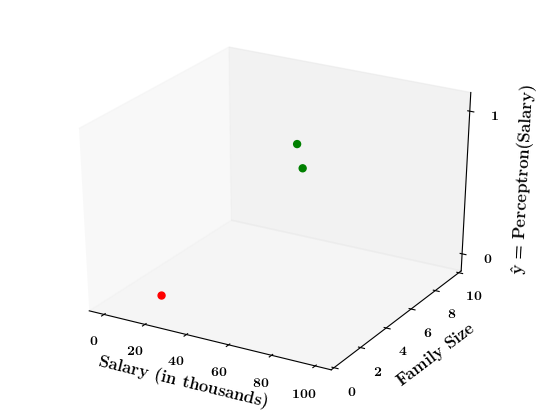
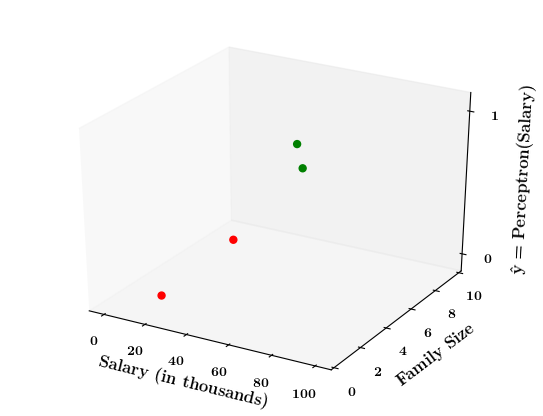
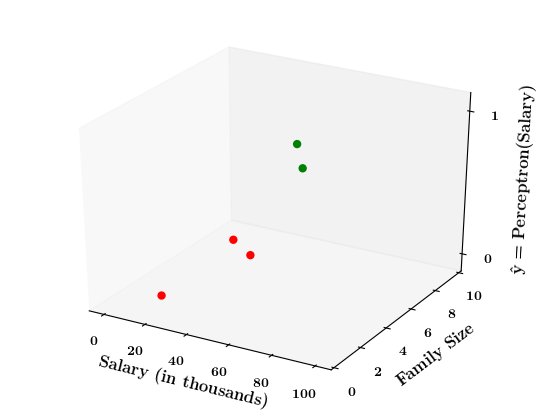
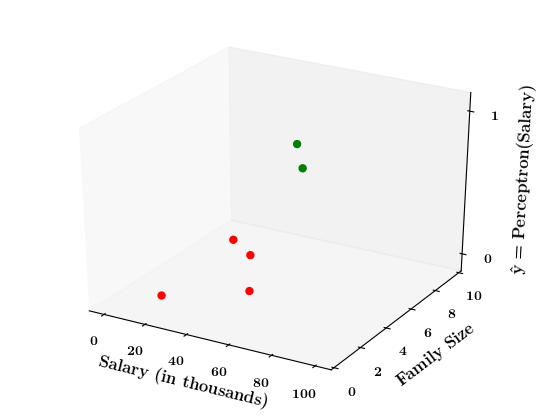
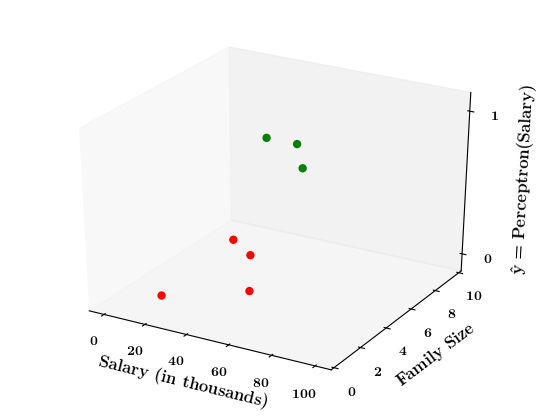
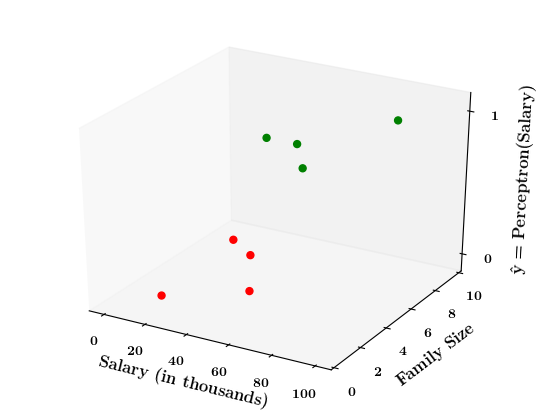
Limitations of Perceptron

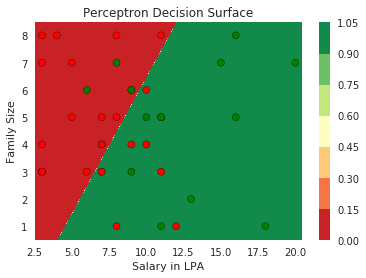
What if the data is not linearly separable ?

(c) One Fourth Labs

y=\sum_{i=1}^n w_i x_i \geq b

y=\sum_{i=1}^n w_i x_i \geq b

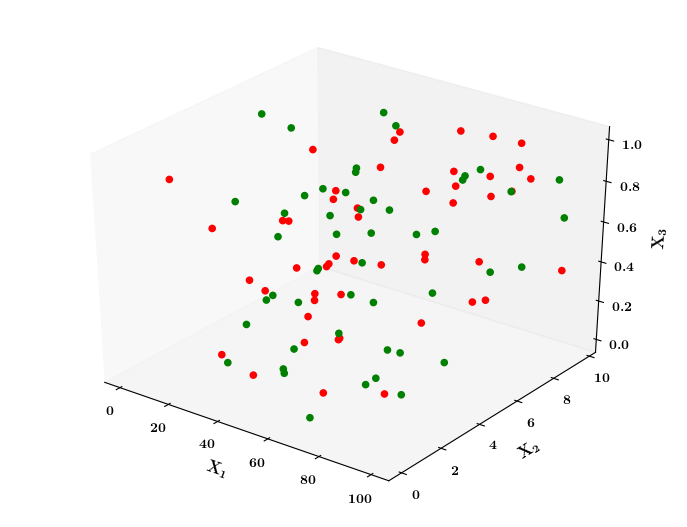
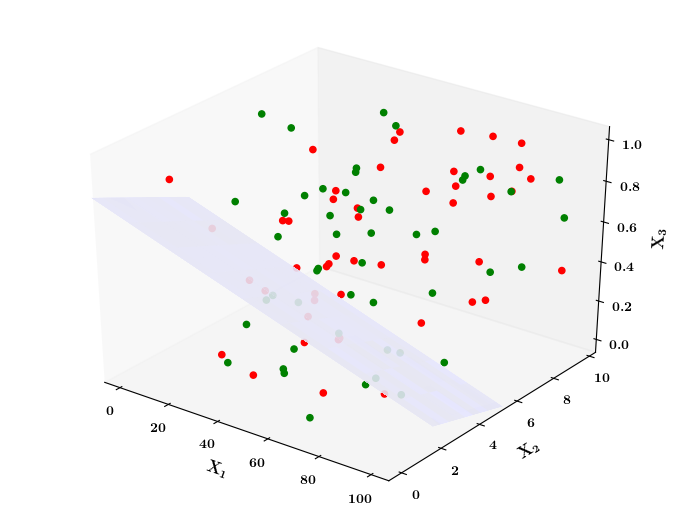
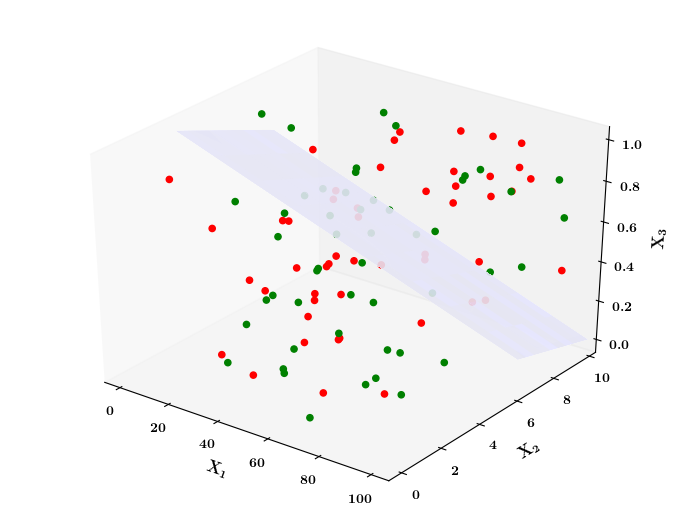
Limitations of Perceptron

Isn't the perceptron model a bit harsh at the boundaries ?

(c) One Fourth Labs

Isn't it a bit odd that a person with 50.1K salary will buy a car but someone with 49.9K will not buy a car ?

Salary ( in thousands)	Can buy a car?
80	1
20	0
65	1
15	0
30	0
49	0
51	1
87	1

y=\sum_{i=1}^n w_i x_i \geq b

y=\sum_{i=1}^n w_i x_i \geq b

\text{Suppose,} \\ \mathbb{w_1} = 2,\\ \hspace{-0.2cm}\mathbb{b}\ \ = 1

\text{Suppose,} \\ \mathbb{w_1} = 2,\\ \hspace{-0.2cm}\mathbb{b}\ \ = 1

(c) One Fourth Labs

The Road Ahead

What's going to change now ?

(c) One Fourth Labs

\( \{0, 1\} \)

Boolean

Accuracy=\frac{\text{Number of correct predictions}}{\text{Total number of predictions}}

Accuracy=\frac{\text{Number of correct predictions}}{\text{Total number of predictions}}

Loss

Model

Data

Task

Evaluation

Learning

Linear

Real inputs

Boolean output

loss = \sum_i max(0,1-y_i*\hat{y_i})

loss = \sum_i max(0,1-y_i*\hat{y_i})

Specific learning algorithm

Harsh at boundaries

Real output

Non-linear

A more generic learning algorithm

Smooth at boundaries

Data and Task

What kind of data and tasks can Perceptron process ?

(c) One Fourth Labs

Data and Task

What kind of data and tasks can Perceptron process ?

(c) One Fourth Labs

Real inputs

Launch (within 6 months)	0	1	1	0	0	1	0	1	1
Weight (g)	151	180	160	205	162	182	138	185	170
Screen size (inches)	5.8	6.18	5.84	6.2	5.9	6.26	4.7	6.41	5.5
dual sim	1	1	0	0	0	1	0	1	0
Internal memory (>= 64 GB, 4GB RAM)	1	1	1	1	1	1	1	1	1
NFC	0	1	1	0	1	0	1	1	1
Radio	1	0	0	1	1	1	0	0	0
Battery(mAh)	3060	3500	3060	5000	3000	4000	1960	3700	3260
Price (INR)	15k	32k	25k	18k	14k	12k	35k	42k	44k
Like (y)	1	0	1	0	1	1	0	1	0

Model

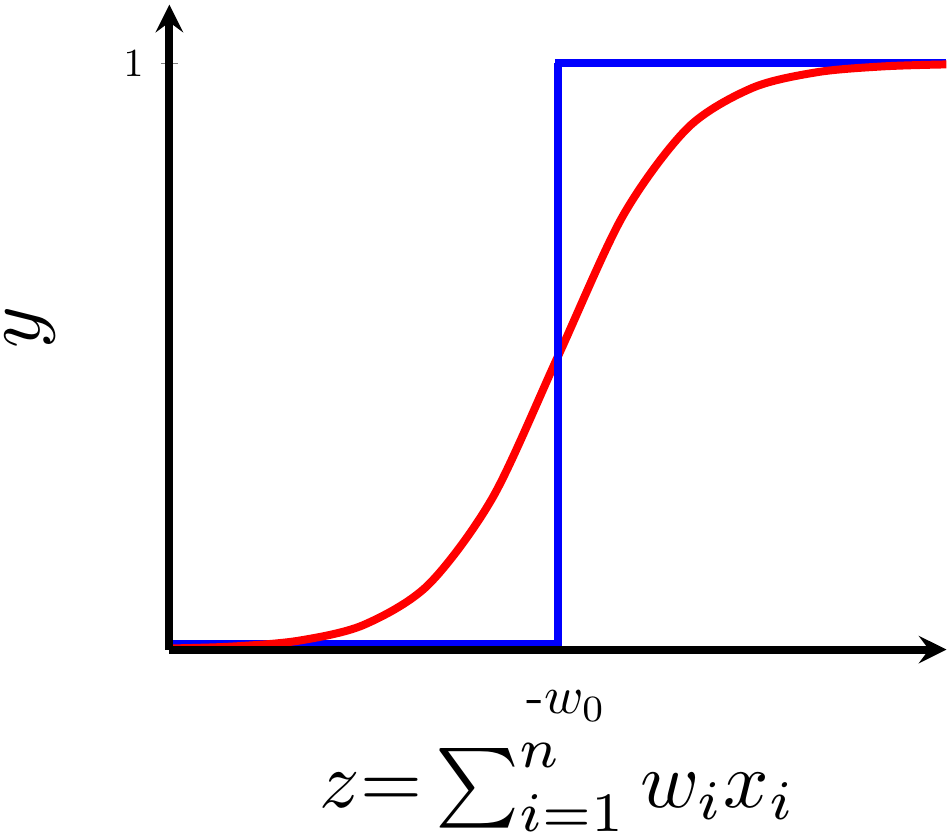
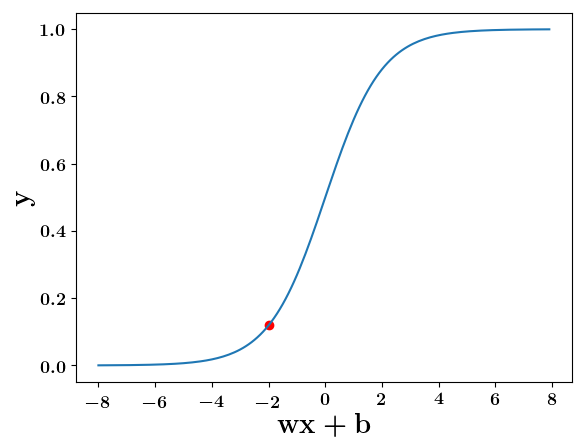
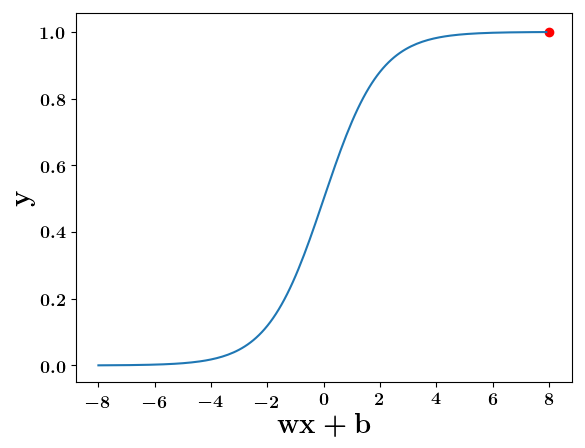
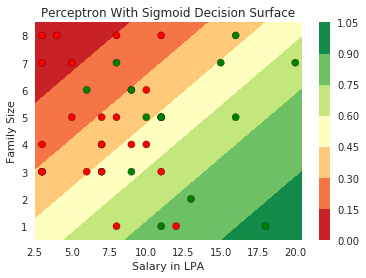
Can we have a smoother (not-so-harsh) function ?

(c) One Fourth Labs

y = \dfrac{1}{1 + e^{-(wx +b)}}

y = \dfrac{1}{1 + e^{-(wx +b)}}

wx+b=0, y=0.5

wx+b=0, y=0.5

wx+b=-2, y=0.12

wx+b=-2, y=0.12

wx+b=2, y=0.88

wx+b=2, y=0.88

wx+b=8, y=0.9997

wx+b=8, y=0.9997

wx+b=-8, y=0.0003

wx+b=-8, y=0.0003

Model

What happens when we have more than 1 input ?

(c) One Fourth Labs

Launch (within 6 months)	0	1	1	0	0	1	0	1	1
Weight (<160g)	1	0	1	0	0	0	1	0	0
Screen size (<5.9 in)	1	0	1	0	1	0	1	0	1
dual sim	1	1	0	0	0	1	0	1	0
Internal memory (>= 64 GB, 4GB RAM)	1	1	1	1	1	1	1	1	1
NFC	0	1	1	0	1	0	1	1	1
Radio	1	0	0	1	1	1	0	0	0
Battery(>3500mAh)	0	0	0	1	0	1	0	1	0
Price > 20k	0	1	1	0	0	0	1	1	1
Like (y)	1	0	1	0	1	1	0	1	0

Launch (within 6 months)	0	1	1	0	0	1	0	1	1
Weight (<160g)	1	0	1	0	0	0	1	0	0
Screen size (<5.9 in)	1	0	1	0	1	0	1	0	1
dual sim	1	1	0	0	0	1	0	1	0
Internal memory (>= 64 GB, 4GB RAM)	1	1	1	1	1	1	1	1	1
NFC	0	1	1	0	1	0	1	1	1
Radio	1	0	0	1	1	1	0	0	0
Battery(>3500mAh)	0	0	0	1	0	1	0	1	0
Price > 20k	0	1	1	0	0	0	1	1	1
Like (y)	1	0	1	0	1	1	0	1	0
Prediction	0	0	1	0	0	1	1	1	0

\hat{y}

\hat{y}

y = \frac{1}{1 + e^{-(\sum_i w_ix_i +b)}}

y = \frac{1}{1 + e^{-(\sum_i w_ix_i +b)}}

y = \frac{1}{1 + e^{(-w^Tx+b)}}

y = \frac{1}{1 + e^{(-w^Tx+b)}}

w^Tx+b=0, y=0.5

w^Tx+b=0, y=0.5

w^Tx+b=2, y=0.88

w^Tx+b=2, y=0.88

w^Tx+b=-2, y=0.12

w^Tx+b=-2, y=0.12

Model

How does this help when the data is not linearly separable ?

(c) One Fourth Labs

Still does not completely solve our problem but we will slowly get there!

2. Show the sigmoid model equations here

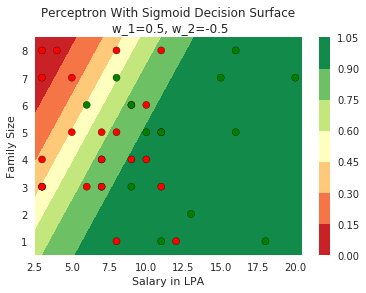
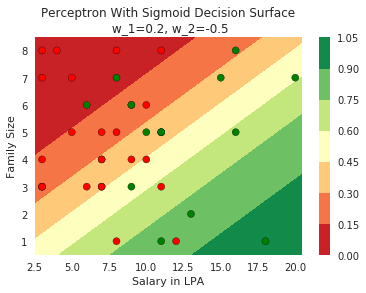
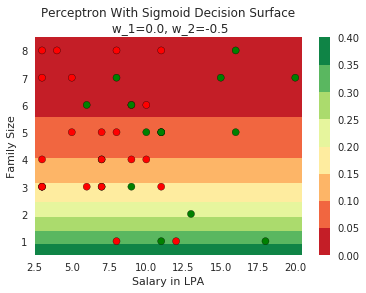
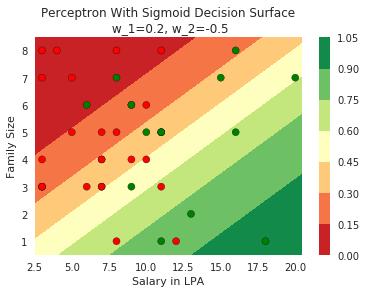
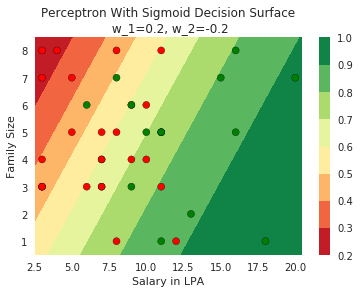
Model

What about extreme non-linearity ?

(c) One Fourth Labs

Still does not completely solve our problem but we will slowly get there with more complex models!

1.Now show a case where the blue and red points are completely mixed with each other

2. show that no matter how you adjust w_1 and w_2 you will not be able to find any separation between blue and red points

3. Now show the quote at RHS bottom using our cartoon person

2. Show the sigmoid model equations here

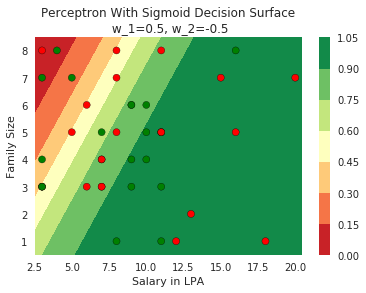
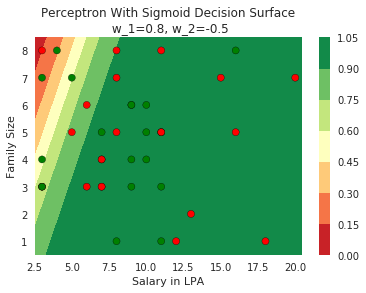
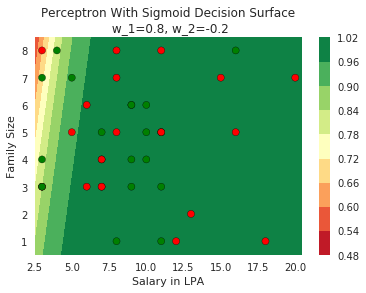
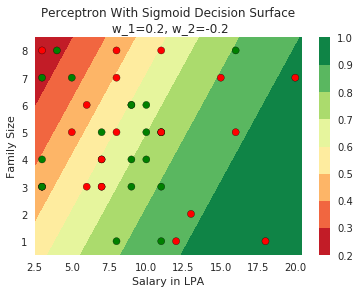
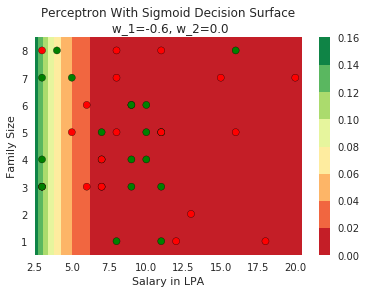
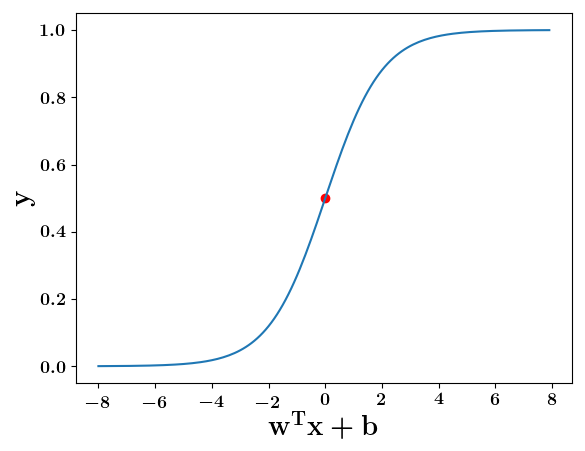
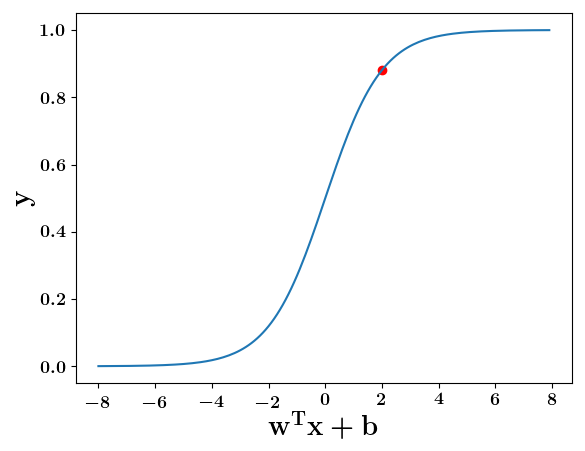
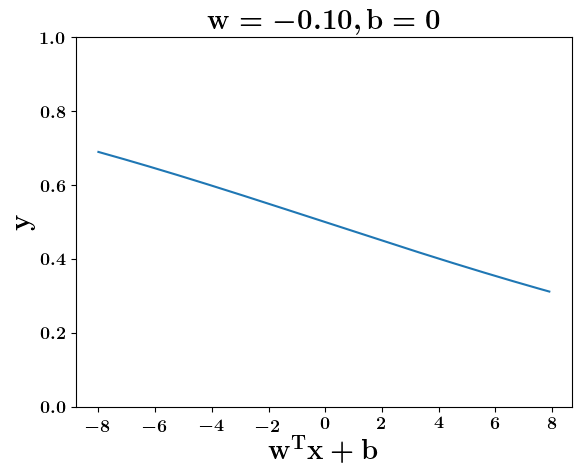
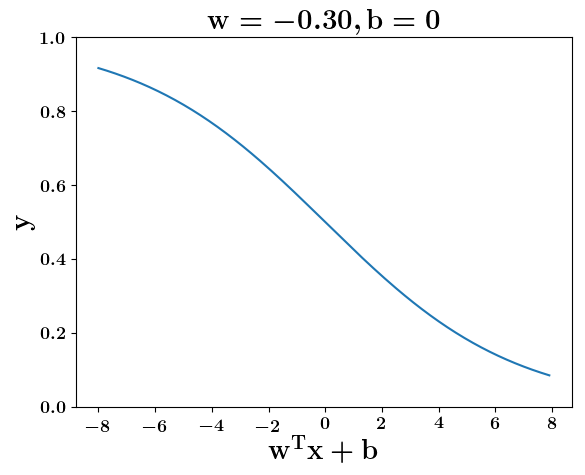
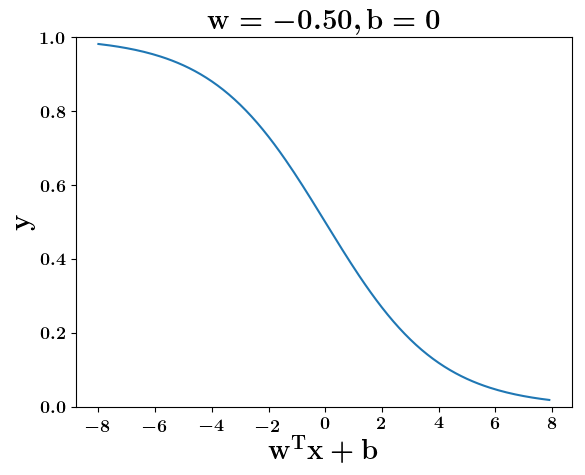
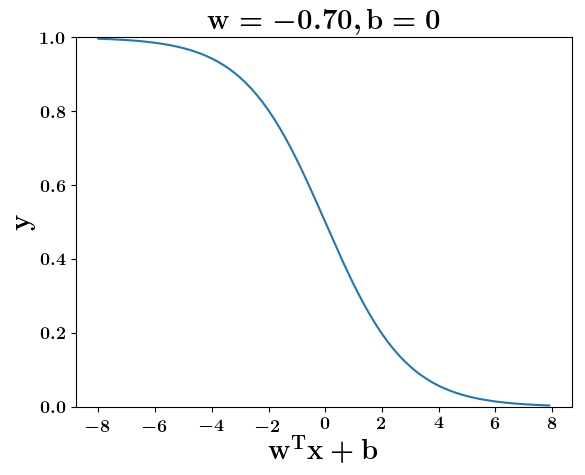
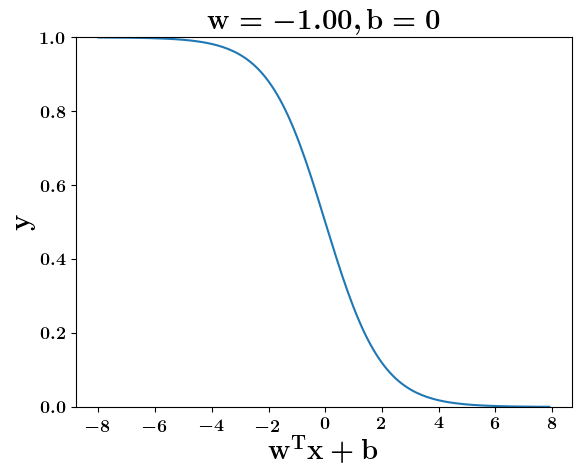
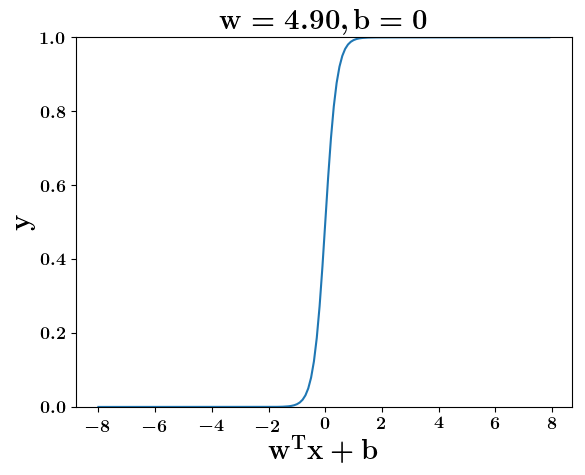
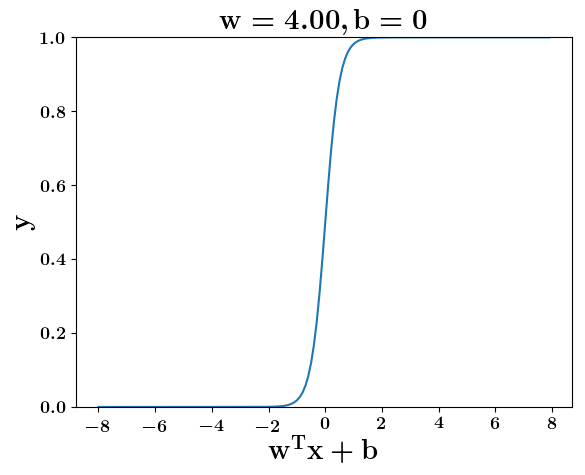
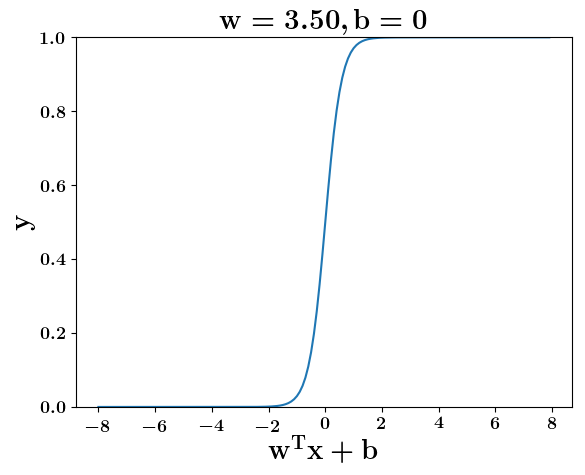
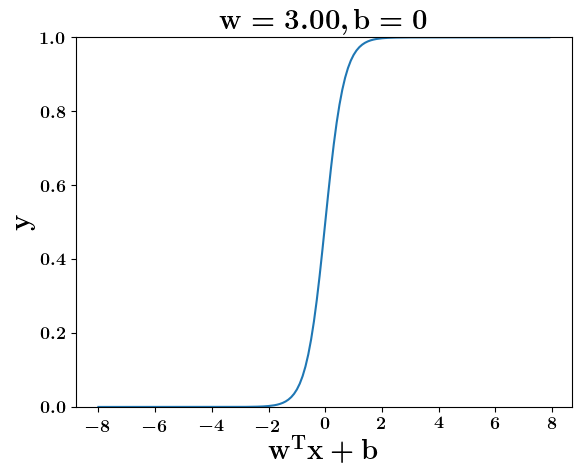
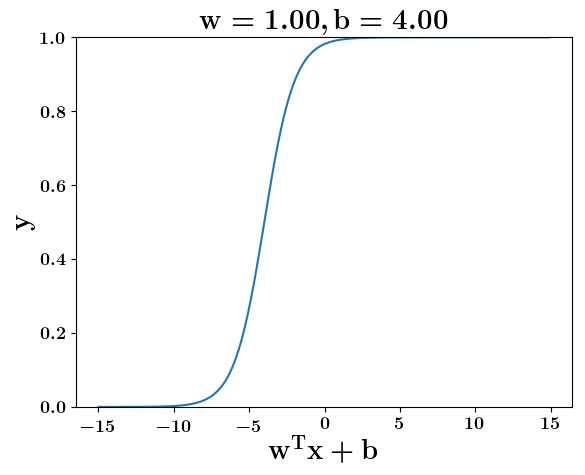
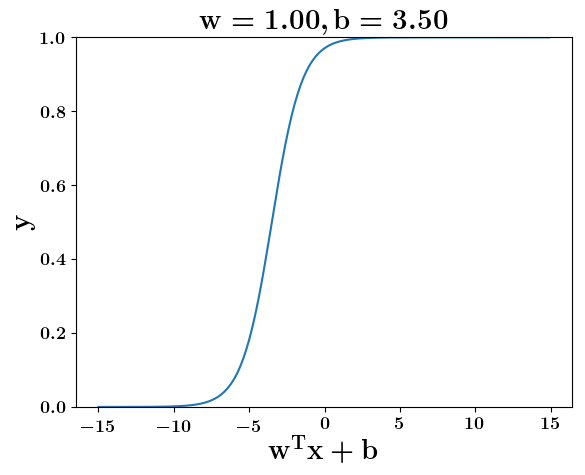
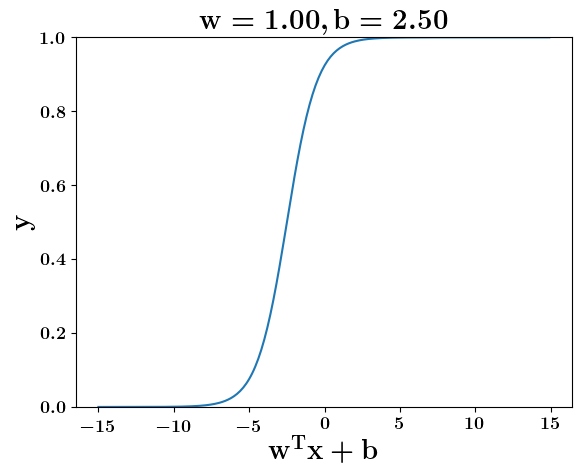
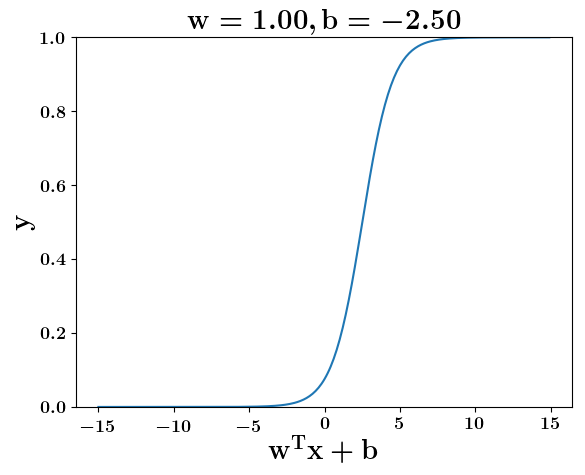
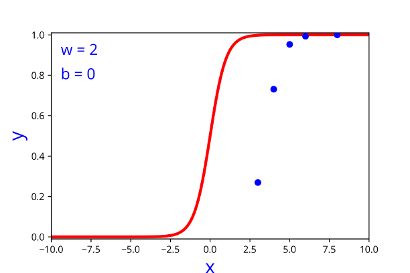
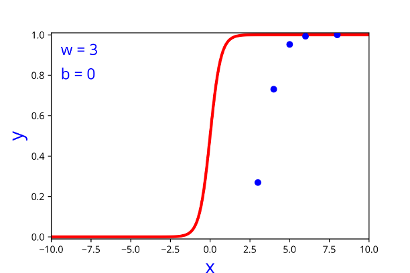
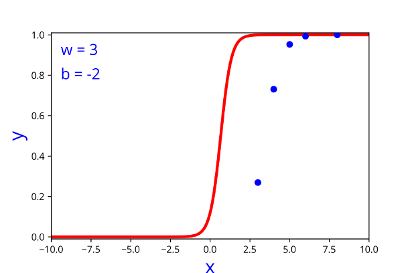
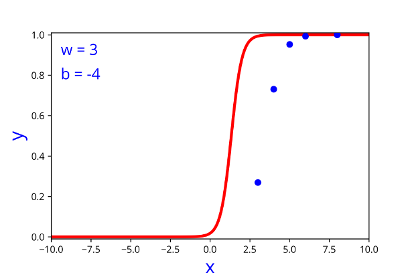
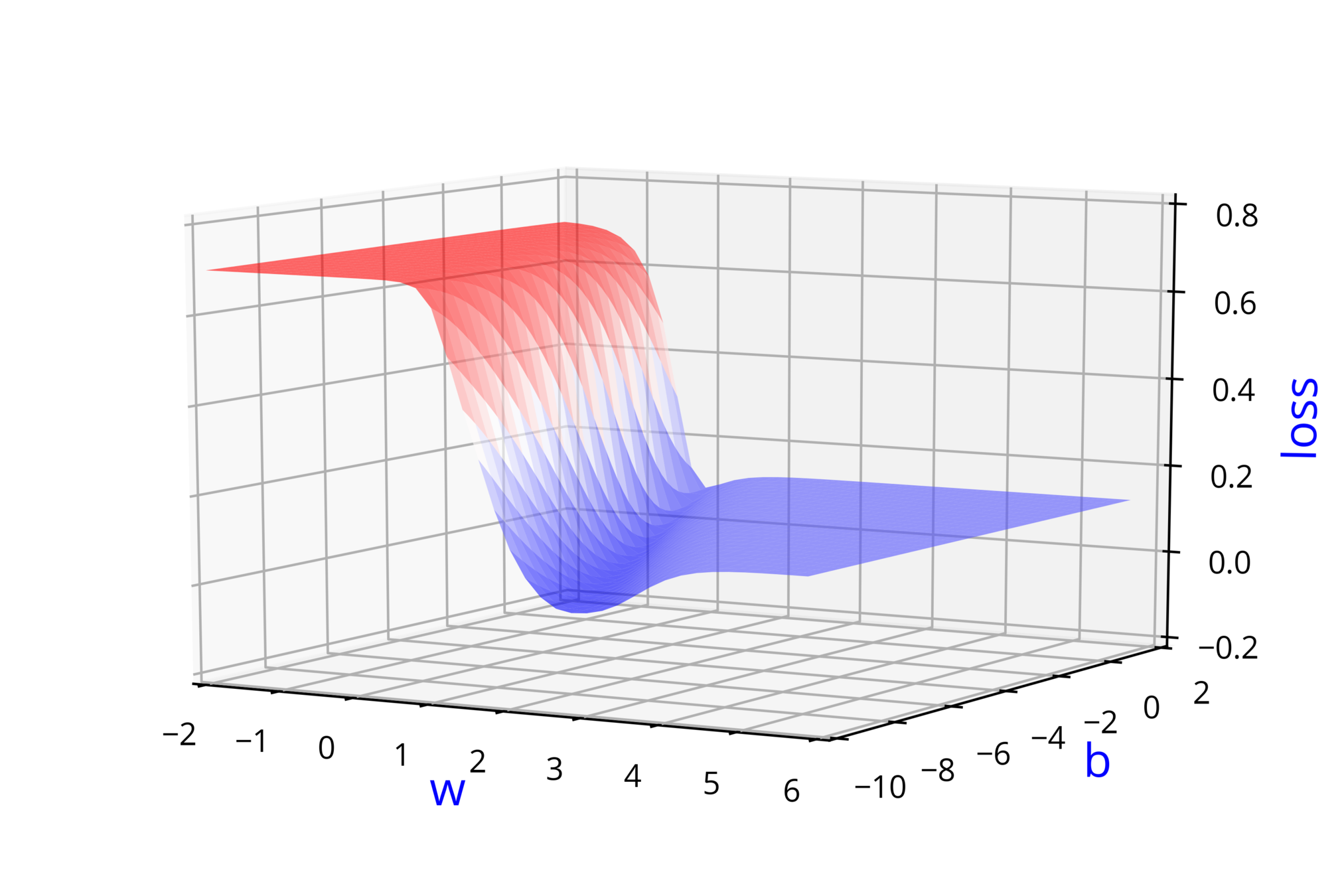
Model

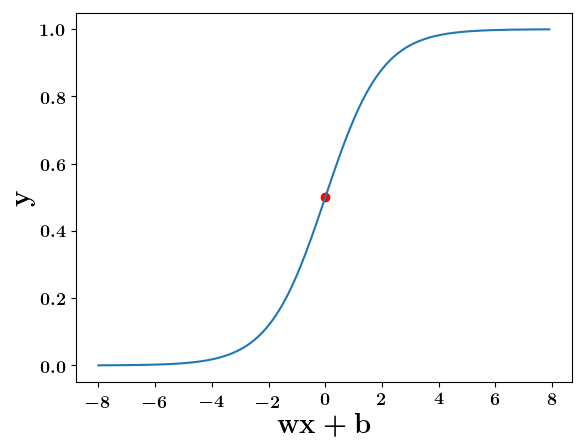
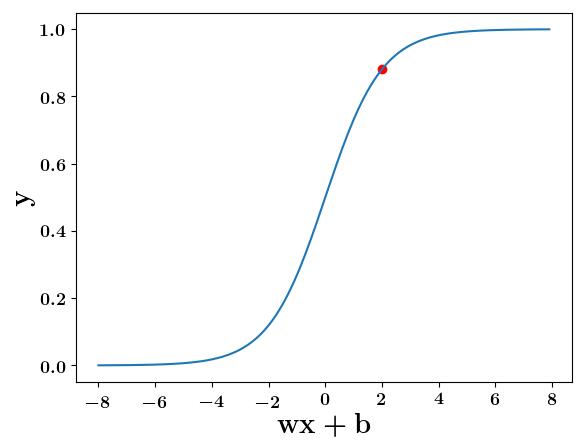
How does the function behave when we change w and b

(c) One Fourth Labs

y =\frac{1}{1+e^{-(wx+b)}}=\frac{1}{2}\\ \implies e^{-(wx+b)} = 1\\ \implies wx+b=0\\ \implies x=-\frac{b}{w}

y =\frac{1}{1+e^{-(wx+b)}}=\frac{1}{2}\\ \implies e^{-(wx+b)} = 1\\ \implies wx+b=0\\ \implies x=-\frac{b}{w}

y = \frac{1}{1 + e^{(-w^Tx+b)}}

y = \frac{1}{1 + e^{(-w^Tx+b)}}

At what value of x is the value of sigmoid(X) = 0.5

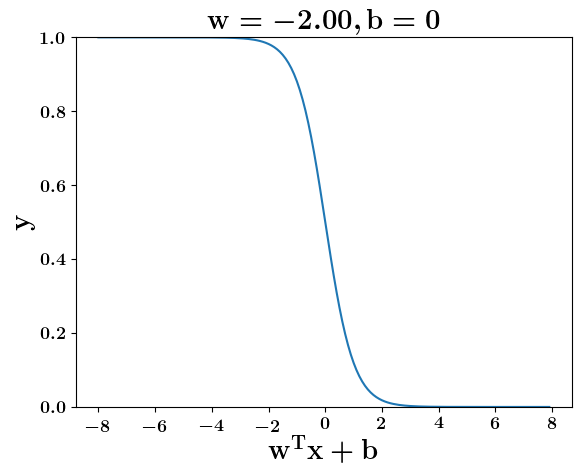
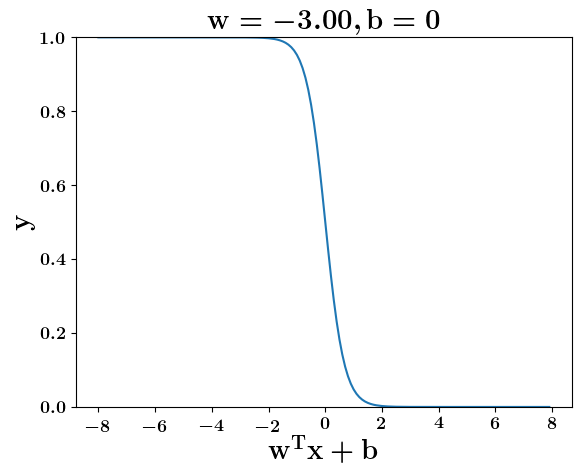
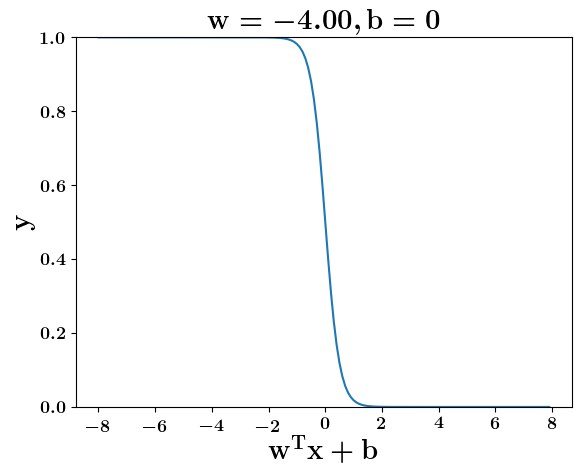
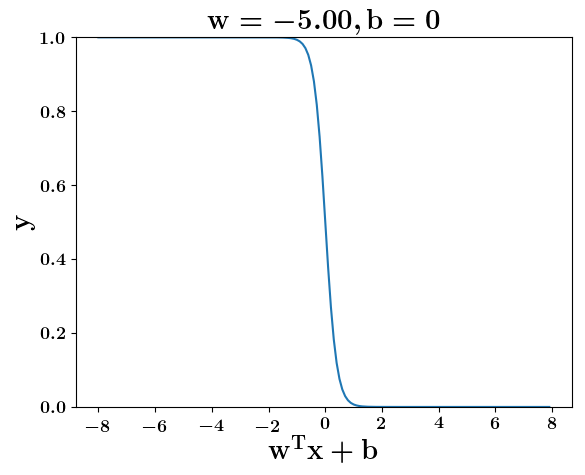
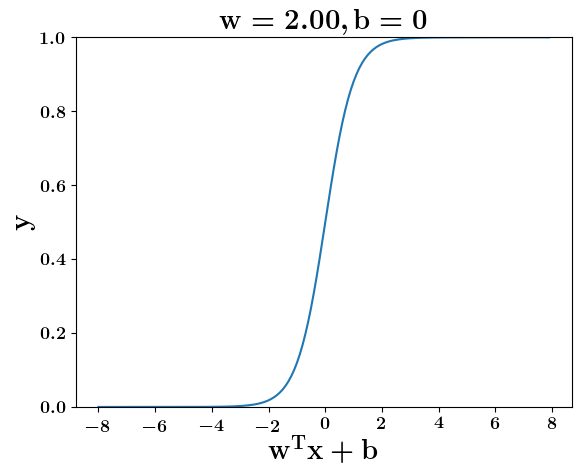
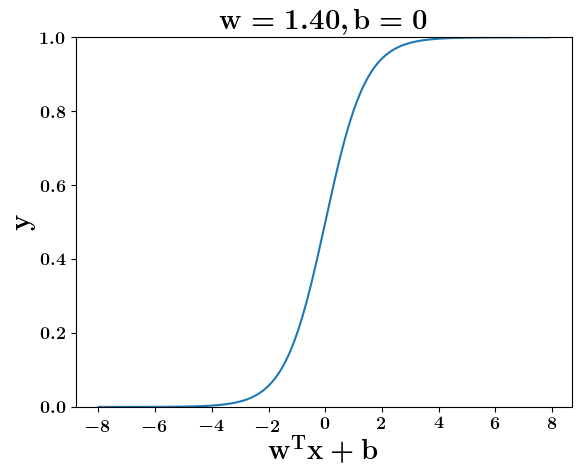
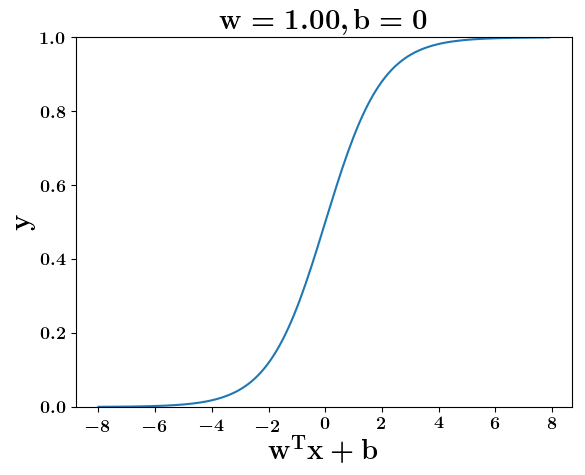
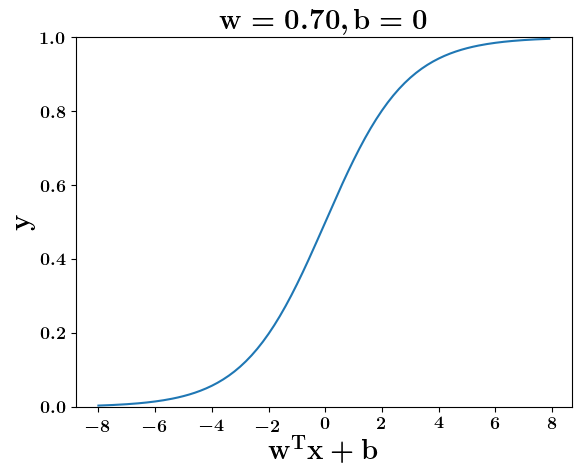
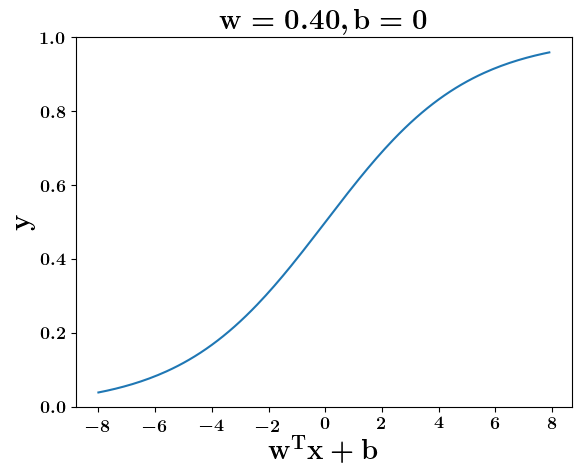
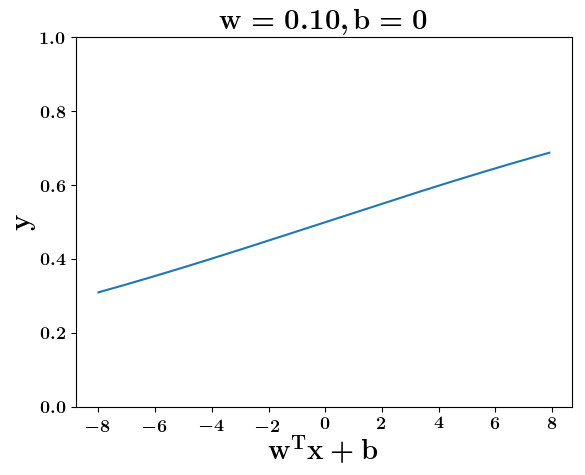
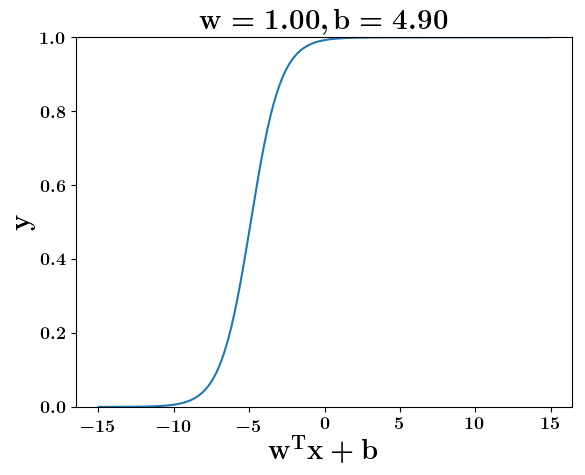
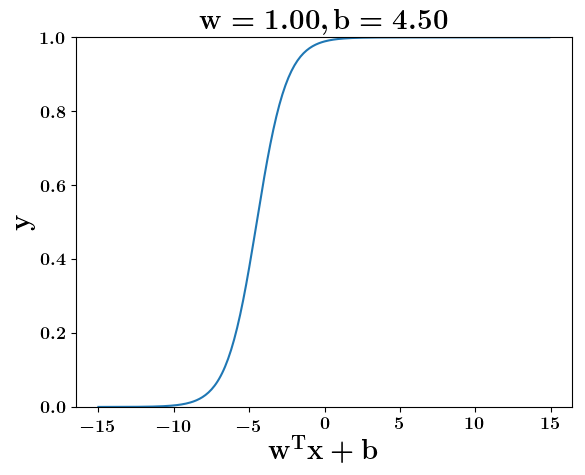
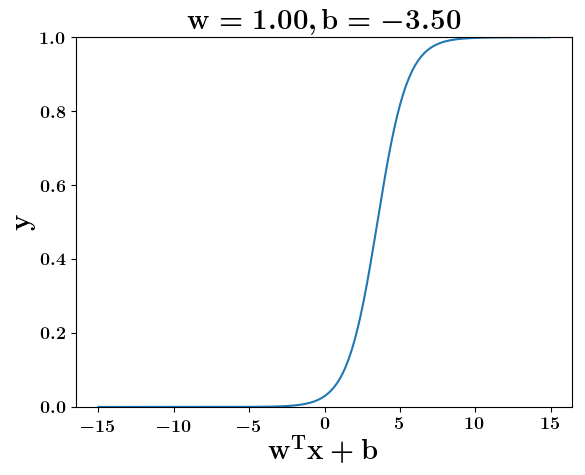
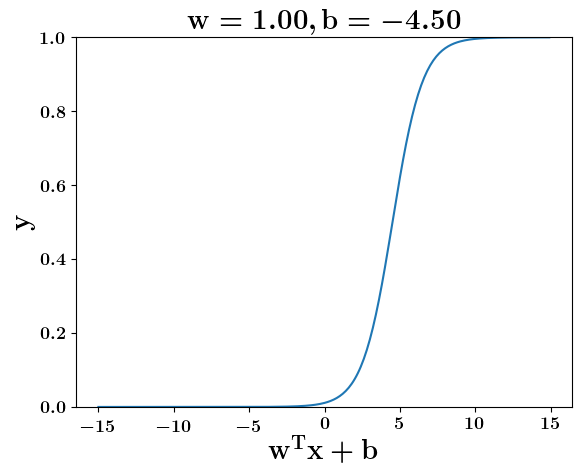
Loss Function

What is the loss function that you use for this model ?

(c) One Fourth Labs

Can we use loss functions which represent the solution to the problem better? For example, is a bi-quadratic loss a good choice? We will see this later in the course.


1	1	0.5	0.6
2	1	0.8	0.7
1	2	0.2	0.2
2	2	0.9	0.5

\hat{y}

\hat{y}

x_1

x_1

x_2

x_2

y

Loss=\sum_{i=1}^{4} (y-\hat{y})^2=0.18

Loss=\sum_{i=1}^{4} (y-\hat{y})^2=0.18

\hat{y} = \dfrac{1}{1 + e^{-(wx +b)}}

\hat{y} = \dfrac{1}{1 + e^{-(wx +b)}}

Learning Algorithm

Can we try to estimate w, b using some guess work ?

(c) One Fourth Labs

Initialise

Iterate over data:

till satisfied

\( h = \frac{1}{1+e^{-(w*x + b)}} \)

I/P	O/P
2	0.047
3	0.268
4	0.73
5	0.952
8	0.999

\(w, b \)

\( guess\_and\_update(x_i) \)

w	b

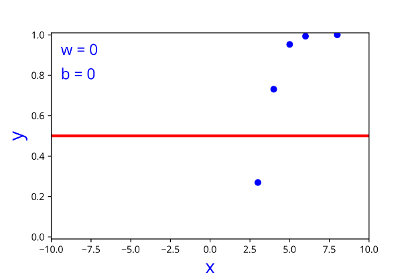
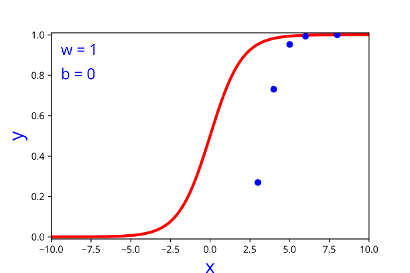
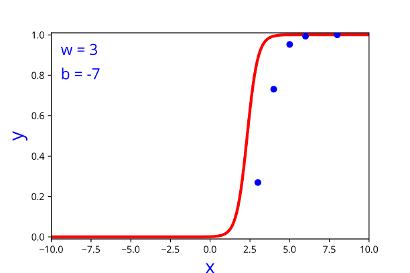
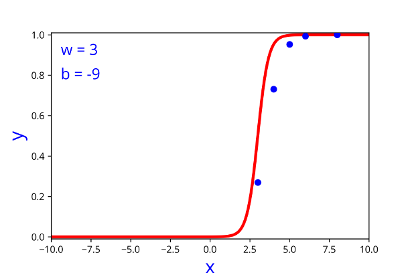
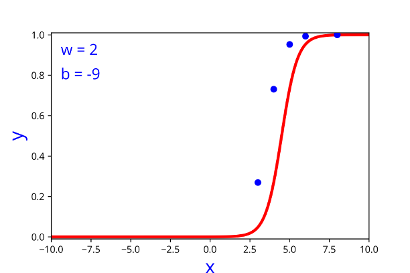
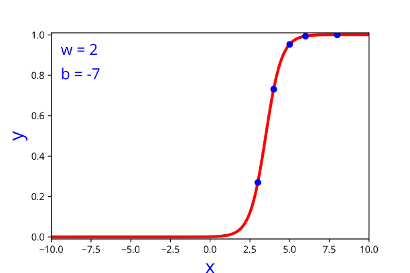
w	b
1	0

w	b
0	0

w	b
2	0

w	b
3	-7

w	b
3	-4

w	b
3	-2

w	b
3	0

w	b
3	-9

w	b
2	-9

w	b
2	-7

Learning Algorithm

Can we take a closer look at what we just did ?

(c) One Fourth Labs

Initialise

Iterate over data:

till satisfied

\(w, b \)

\( guess\_and\_update(x_i) \)

w	b

w	b
1	0

w	b
0	0

w	b
2	0

w	b
3	-7

w	b
3	-4

w	b
3	-2

w	b
3	0

w	b
3	-9

w	b
2	-9

\( w = w + \Delta w \\ b = b + \Delta b \)

w	b
2	-7

1 = 0 + \(\Delta\)1

0 = 0 + \( \Delta\)0

2 = 1 + \(\Delta\)1

0 = 0 + \( \Delta\)0

3 = 2 + \(\Delta\)1

0 = 0 + \( \Delta\)0

3 = 3 + \(\Delta\)0

-2 = 0 + \( \Delta\)-2

3 = 3 + \(\Delta\)0

-4 = -2 + \( \Delta\)-2

3 = 3 + \(\Delta\)0

-7 = -4 + \( \Delta\)-3

3 = 3 + \(\Delta\)0

-9 = -7 + \( \Delta\)-2

2 = 3 + \(\Delta\)-1

-9 = -7 + \( \Delta\)-2

2 = 3 + \(\Delta\)-1

-7 = -9 + \( \Delta\)2

w = 0

b = 0

\( w = w + \Delta w \)

\( b = b + \Delta b \)

\( \Delta w = some\_guess \)

\( \Delta b = some\_guess \)

Learning Algorithm

Can we connect this to the loss function ?

(c) One Fourth Labs

Initialise

Iterate over data:

till satisfied

\(w, b \)

\( guess\_and\_update(x_i) \)

\( w = w + \Delta w \\ b = b + \Delta b \)

1 = 0 + \(\Delta\)1

0 = 0 + \( \Delta\)0

2 = 1 + \(\Delta\)1

0 = 0 + \( \Delta\)0

3 = 2 + \(\Delta\)1

0 = 0 + \( \Delta\)0

3 = 3 + \(\Delta\)0

-2 = 0 + \( \Delta\)-2

3 = 3 + \(\Delta\)0

-4 = -2 + \( \Delta\)-2

3 = 3 + \(\Delta\)0

-7 = -4 + \( \Delta\)-3

3 = 3 + \(\Delta\)0

-9 = -7 + \( \Delta\)-2

2 = 3 + \(\Delta\)-1

-9 = -7 + \( \Delta\)-2

2 = 3 + \(\Delta\)-1

-7 = -9 + \( \Delta\)2

w = 0

b = 0

\( w = w + \Delta w \)

\( b = b + \Delta b \)

w	b	Loss

w	b	Loss
0	0	0.1609

w	b	Loss
1	0	0.1064

w	b	Loss
2	0	0.1210

w	b	Loss
3	0	0.1217

w	b	Loss
3	-2	0.1215

w	b	Loss
3	-4	0.1198

w	b	Loss
3	-7	0.1081

w	b	Loss
3	-9	0.0209

w	b	Loss
2	-9	0.0636

w	b	Loss
2	-7	0.000

Indeed we were using the loss function to guide us in finding \( \Delta w\) and \(\Delta b\)

Learning Algorithm

Can we visualise this better ?

(c) One Fourth Labs

Initialise

Iterate over data:

till satisfied

\(w, b \)

\( guess\_and\_update(x_i) \)

\( w = w + \Delta w \\ b = b + \Delta b \)

1 = 0 + \(\Delta\)1

0 = 0 + \( \Delta\)0

2 = 1 + \(\Delta\)1

0 = 0 + \( \Delta\)0

3 = 2 + \(\Delta\)1

0 = 0 + \( \Delta\)0

3 = 3 + \(\Delta\)0

-2 = 0 + \( \Delta\)-2

3 = 3 + \(\Delta\)0

-4 = -2 + \( \Delta\)-2

3 = 3 + \(\Delta\)0

-7 = -4 + \( \Delta\)-3

3 = 3 + \(\Delta\)0

-9 = -7 + \( \Delta\)-2

2 = 3 + \(\Delta\)-1

-9 = -7 + \( \Delta\)-2

2 = 3 + \(\Delta\)-1

-7 = -9 + \( \Delta\)2

w = 0

b = 0

\( w = w + \Delta w \)

\( b = b + \Delta b \)

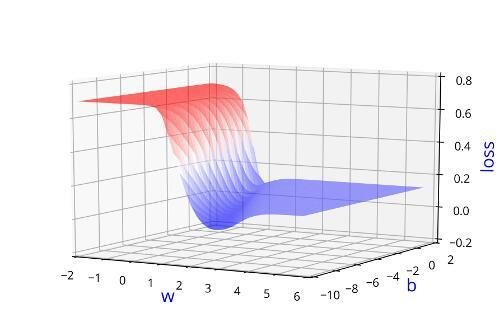
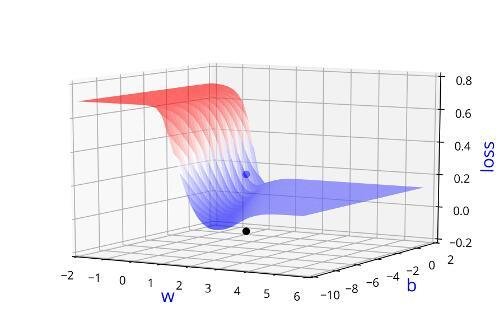
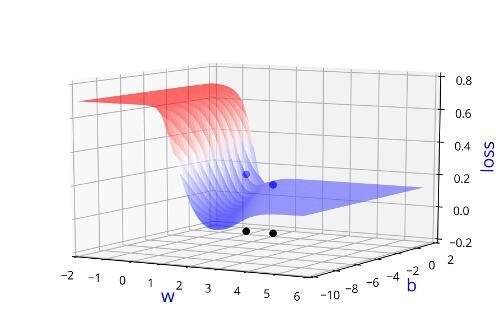
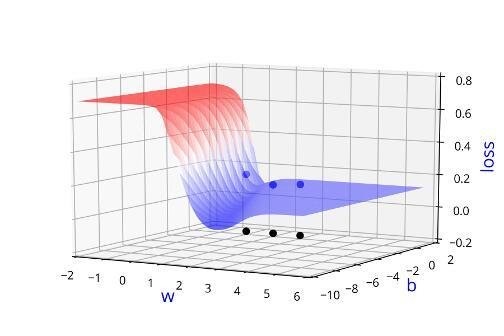
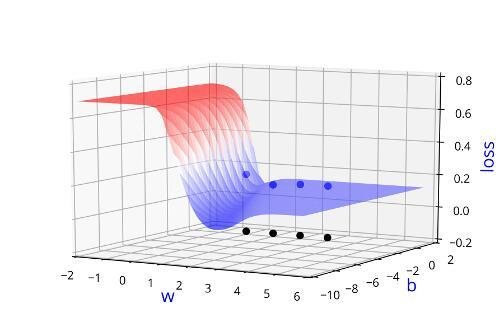
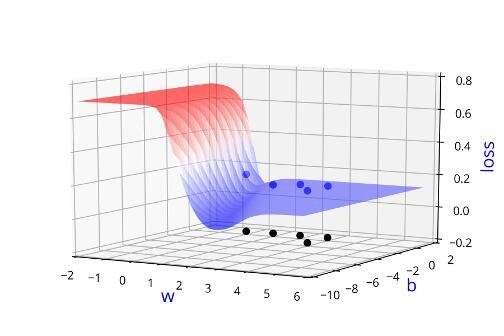
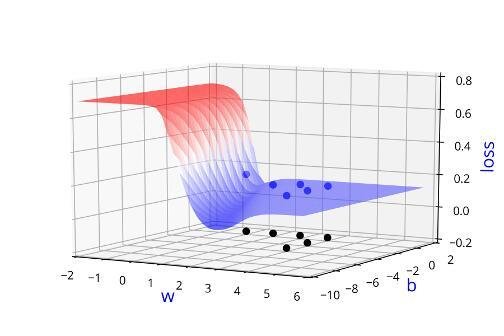
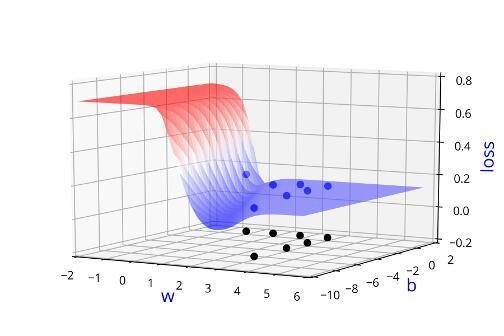
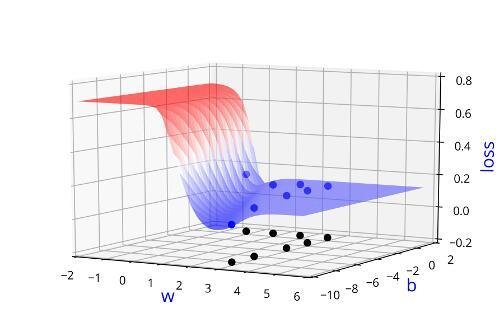
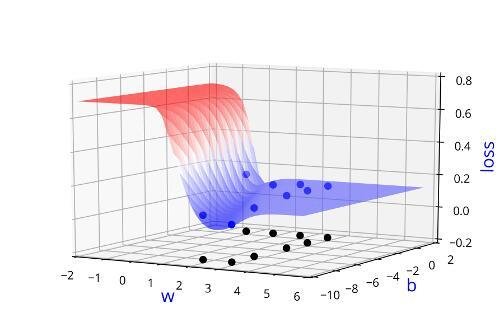
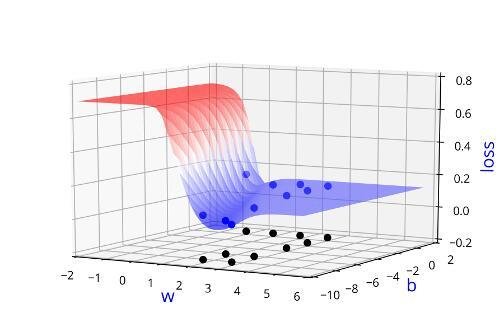
Learning Algorithm

(c) One Fourth Labs

Initialise

Iterate over data:

till satisfied

\(w, b \)

\( guess\_and\_update(x_i) \)

w	b

w	b
1	0

w	b
0	0

w	b
2	0

w	b
3	-7

w	b
3	-4

w	b
3	-2

w	b
3	0

w	b
3	-9

w	b
2	-9

\( w = w + \Delta w \\ b = b + \Delta b \)

w	b
2	-7

1 = 0 + \(\Delta\)1

0 = 0 + \( \Delta\)0

2 = 1 + \(\Delta\)1

0 = 0 + \( \Delta\)0

3 = 2 + \(\Delta\)1

0 = 0 + \( \Delta\)0

3 = 3 + \(\Delta\)0

-2 = 0 + \( \Delta\)-2

3 = 3 + \(\Delta\)0

-4 = -2 + \( \Delta\)-2

3 = 3 + \(\Delta\)0

-7 = -4 + \( \Delta\)-3

3 = 3 + \(\Delta\)0

-9 = -7 + \( \Delta\)-2

2 = 3 + \(\Delta\)-1

-9 = -7 + \( \Delta\)-2

2 = 3 + \(\Delta\)-1

-7 = -9 + \( \Delta\)2

w = 0

b = 0

\( w = w + \Delta w \)

\( b = b + \Delta b \)

\( \Delta w = some\_guess \)

\( \Delta b = some\_guess \)

"Instead of guessing \( \Delta w\) and \(\Delta b\), we need a principled way of changing w and b based on the loss function"

What is our aim now ?

Learning Algorithm

Can we formulate this more mathematically ?

(c) One Fourth Labs

\(\theta = [w, b] \)

\(\Delta \theta = [\Delta w, \Delta b] \)

\( \theta_{new} = \theta + \eta . \Delta \theta \)

\(\theta\)

\(\Delta \theta\)

\( \eta . \Delta \theta \)

\( \theta_{new}\)

Instead of guessing \(\Delta w\) and\( \Delta\) b, we need a principled way of changing w and b based on the loss function

Learning Algorithm

Can we get the answer from some basic mathematics ?

(c) One Fourth Labs

\( \because \theta = [w, b] \)

\(w \rightarrow w + \eta \Delta w \)

\(b \rightarrow b + \eta \Delta b \)

\(\mathscr{L} (w) < \mathscr{L}(w +\eta \Delta w)\)

\( \mathscr{L} (b) < \mathscr{L}(b +\eta \Delta b)\)

\(\mathscr{L} ( \theta) < \mathscr{L}( \theta + \eta \Delta \theta)\)

\( f(x + \Delta x) = f(x) + f'(x)\Delta x + \frac{1}{2!}f''(x)\Delta x^2 + \frac{1}{3!}f'''(x)\Delta x^3 + \cdots \)

Taylor Series

\(\mathscr{L} (w,b) < \mathscr{L}(w +\eta \Delta w, b + \eta\Delta b )\)

\( \mathscr{L}(\theta + \Delta \theta) = \mathscr{L}(\theta) + \mathscr{L}'(\theta)\Delta \theta + \frac{1}{2!}\mathscr{L}''(\theta)\Delta \theta^2 + \frac{1}{3!}\mathscr{L}'''(\theta)\Delta \theta^3 + \cdots \)

Learning Algorithm

How does Taylor series help us to arrive at the answer ?

(c) One Fourth Labs

\(\mathscr{L}(\theta+\eta u) = \mathscr{L}(\theta) + \eta*u^T \nabla_{\theta} \mathscr{L}(\theta) + \frac{\eta^2}{2!}*u^T \nabla^2 \mathscr{L} (\theta)u + \frac{\eta^3}{3!}*....+ \frac{\eta^4}{4!}*...\)

\(= \mathscr{L}(\theta)+ \eta*u^T \nabla_{\theta}\mathscr{L}(\theta) [\eta is typically small, so \eta^2, \eta^3, ... \rightarrow 0]\)

Note that the move \( \eta u \) would be favorable only if,

\( \mathscr{L}(\theta+\eta u) - \mathscr{L}(\theta) < 0\) [ i.e. if the new loss is less than the previous loss]

This implies,

\( u^T \nabla_{\theta} \mathscr{L}(\theta) < 0 \)

For ease of notation,

let \( \Delta\theta = u\),

Then from Taylor series, we have,

Learning Algorithm

How does Taylor series help us to arrive at the answer ?

(c) One Fourth Labs

Okay, so we have,

\( u^T \nabla_{\theta} \mathscr{L}(\theta) < 0 \)

But, what is the range of \(u^T \nabla_{\theta}\mathscr{L}(\theta) \) ?

Let \(\beta\) be the angle between \(u\) and \(\nabla_{\theta}\mathscr{L}(\theta)\), then we know that,

\(-1 \leq cos(\beta) = \frac{u^T \nabla_{\theta}\mathscr{L}(\theta)}{||u||*||\nabla_{\theta}\mathscr{L}(\theta)||} \leq 1\)

multiply throughout by k = \( ||u||*||\nabla_{\theta}\mathscr{L}(\theta)||\)

\( -k \leq k*cos(\beta) = u^T \nabla_{\theta}\mathscr{L}(\theta) \leq k \)

Thus, \( \mathscr{L}(\theta + \eta u) - \mathscr{L}(\theta) = u^T \nabla_{\theta}\mathscr{L}(\theta) = k*\cos \beta \) will be most negative

when \(\cos(\beta)\) = -1 i.e., when \(\beta\) is 180\(\degree \)

Learning Algorithm

How does Taylor series help us to arrive at the answer ?

(c) One Fourth Labs

Gradient Descent Rule,

The direction \(u\) that we intend to move in should be at \(180\degree\) w.r.t. the gradient.
In other words, move in a direction opposite to the gradient.

Parameter Update Rule

\(w_{t+1} = w_{t} - \eta \Delta w_{t} \)

\(b_{t+1} = b_{t} - \eta \Delta b_{t} \)

\( where \Delta w_{t} =\frac{\partial \mathscr{L}(w, b)}{\partial w}_{at w = w_t, b= b_t}, \Delta b_{t} = \frac{\partial \mathscr{L}(w,b)}{\partial b}_{at w = w_t, b = b_t}\)

So we now have a more principled way of moving in the w-b plane than our "guesswork'' algorithm

Learning Algorithm

How does the algorithm look like now ?

(c) One Fourth Labs

Initialise

\(w, b \)

Iterate over data:

\(w_{t+1} = w_{t} - \eta \Delta w_{t} \)

till satisfied

How do I compute \( \Delta w\) and\( \Delta b \)?

\(b_{t+1} = b_{t} - \eta \Delta b_{t} \)

Learning Algorithm

How do I compute \(\Delta w \) and \(\Delta b\)

(c) One Fourth Labs

\(\mathscr{L} = \frac{1}{5} \sum_{i = 1}^{i=5}(f(x_i) - y_i)\)

\(\frac{\partial \mathscr{L}}{\partial w} = \frac{\partial}{\partial w}[ \frac{1}{5} \sum_{i = 1}^{i=5}(f(x_i) - y_i)]\)

\(\Delta w = \frac{\partial \mathscr{L}}{\partial w} = \frac{1}{5} \sum_{i = 1}^{i=5}\frac{\partial}{\partial w} (f(x_i) - y_i)\)

Let's consider only one term in this sum,

Learning Algorithm

How do I compute \(\Delta w \) and \(\Delta b\)

(c) One Fourth Labs

\(\nabla w = \frac{\partial}{\partial w}[\frac{1}{2}*(f(x) - y)^2] \)

\(= \frac{1}{2}*[2*(f(x) - y) * \frac{\partial}{\partial w} (f(x) - y)]\)

\(= (f(x) - y) * \frac{\partial}{\partial w}(f(x)) \)

\(= (f(x) - y) * \frac{\partial}{\partial w}\Big(\frac{1}{1 + e^{-(wx + b)}}\Big) \)

\( = \color{red}{(f(x) - y) * f(x)*(1- f(x)) *x}\)

\( \frac{\partial}{\partial w}\Big(\frac{1}{1 + e^{-(wx + b)}}\Big)\)

\( =\frac{-1}{(1 + e^{-(wx + b)})^2}\frac{\partial}{\partial w}(e^{-(wx + b)})) \)

\( =\frac{-1}{(1 + e^{-(wx + b)})^2}*(e^{-(wx + b)})\frac{\partial}{\partial w}(-(wx + b)))\)

\( =\frac{-1}{(1 + e^{-(wx + b)})}*\frac{e^{-(wx + b)}}{(1 + e^{-(wx + b)})} *(-x)\)

\( =\frac{1}{(1 + e^{-(wx + b)})}*\frac{e^{-(wx + b)}}{(1 + e^{-(wx + b)})} *(x)\)

\( =f(x)*(1- f(x))*x \)

Learning Algorithm

How do I compute \(\Delta w \) and \(\Delta b\)

(c) One Fourth Labs

\(\mathscr{L} = \frac{1}{5} \sum_{i = 1}^{i=5}(f(x_i) - y_i)\)

\(\frac{\partial \mathscr{L}}{\partial w} = \frac{\partial}{\partial w}[ \frac{1}{5} \sum_{i = 1}^{i=5}(f(x_i) - y_i)]\)

\(\Delta w = \frac{\partial \mathscr{L}}{\partial w} = \frac{1}{5} \sum_{i = 1}^{i=5}\frac{\partial}{\partial w} (f(x_i) - y_i)\)

Let's consider only one term in this sum,

\(\Delta w=(f(x) - y) * f(x)*(1- f(x)) *x \)

For 5 points,

\(\Delta w=\sum_{i=1}^{i=5} (f(x_i) - y_i) *f(x_i))*(1- f(x_i)) *x_i \)

\(\Delta b=\sum_{i=1}^{i=5} (f(x_i) - y_i) * f(x_i))*(1- f(x_i)) \)

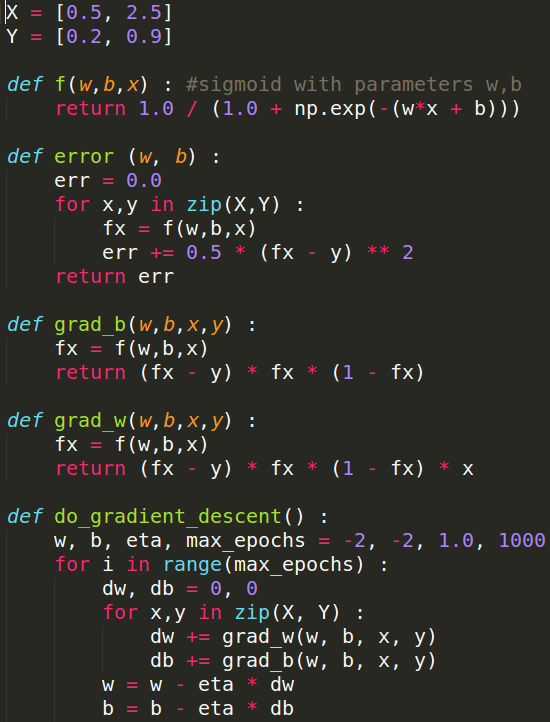
Learning Algorithm

How does the full algorithm look like ?

(c) One Fourth Labs

Learning Algorithm

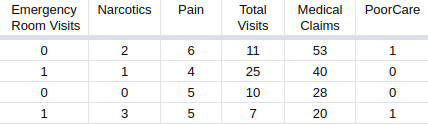
What happens when we have more than 2 parameters ?

(c) One Fourth Labs

\( z = w_1*ER\_visits + w_2*Narcotics + w_3*Pain + w_4*TotalVisits + w_5*MedicalClaims + b \)

\(\hat{y} = \frac{1}{1+e^{-(w_1*x_1 + w_2*x_2 + w_3*x_3 + w_4*x_4 + w_5*x_5 +b)}}\)

\( z = w_1*x_1 + w_2*x_2 + w_3*x_3 + w_4*x_4 + w_5*x_5 + b \)

Initialise

\(w_1, w_2,...,w_5, b \)

Iterate over data:

\(w_1^{t+1} = w_1^{t} - \eta \Delta w_1^{t} \)

till satisfied

\(b_{t+1} = b_{t} - \eta \Delta b_{t} \)

\(w_2^{t+1} = w_2^{t} - \eta \Delta w_2^{t} \)

\(w_5^{t+1} = w_5^{t} - \eta \Delta w_5^{t} \)

\( \vdots \)

\(\Delta w=(f(x) - y) * f(x)*(1- f(x)) *x \)

\(\Delta w_1=(f(x_1,x_2,x_3,x_4,x_5) - y) * f(x_1,x_2,x_3,x_4,x_5)*(1- f(x_1,x_2,x_3,x_4,x_5)) *x_1 \)

\(\hat{y} = \frac{1}{1+e^{-z}}\)

\(\Delta w_1 =(\hat{y} - y) * \hat{y}*(1- \hat{y}) *x_1 \)

Learning Algorithm

How do I compute \(\Delta w \) and \(\Delta b\)

(c) One Fourth Labs

\(\nabla w_1 = \frac{\partial}{\partial w_1}[\frac{1}{2}*(\hat{y} - y)^2] \)

\(= \frac{1}{2}*[2*(\hat{y} - y) * \frac{\partial}{\partial w_1} (\hat{y} - y)]\)

\(= (\hat{y} - y) * \frac{\partial}{\partial w_1}(\hat{y}) \)

\(= (\hat{y} - y) * \frac{\partial}{\partial w_1}\Big(\frac{1}{1 + e^{-(w_1x_1 + w_2x_2 + w_3x_3 + w_4x_4 + w_5x_5 + b)}}\Big) \)

\( = \color{red}{(\hat{y} - y) *\hat{y}*(1- \hat{y}) *x_1}\)

\( \frac{\partial}{\partial w_1}\Big(\frac{1}{1 + e^{-(z)}}\Big)\)

\( =\frac{-1}{(1 + e^{-(z)})^2}\frac{\partial}{\partial w_1}(e^{-(z)})) \)

\( =\frac{-1}{(1 + e^{-(z)})^2}*(e^{-(z)})\frac{\partial}{\partial w_1}(-(z)))\)

\( =\frac{-1}{(1 + e^{-(z)})}*\frac{e^{-(z)}}{(1 + e^{-(z)})} *(-x_1)\)

\( =\frac{1}{(1 + e^{-(z)})}*\frac{e^{-(z)}}{(1 + e^{-(z)})} *(x_1)\)

\( =\hat{y}*(1- \hat{y})*x_1 \)

\( z = w_1*x_1 + w_2*x_2 + w_3*x_3 + w_4*x_4 + w_5*x_5 + b \)

\( \frac{\partial}{\partial w_1}(-z) = - \frac{\partial }{\partial w_1} (w_1*x_1 + w_2*x_2 + w_3*x_3 + w_4*x_4 + w_5*x_5 + b) \)

\( \frac{\partial}{\partial w_1}(-z) = - x_1 \)

Learning Algorithm

How do I compute \(\Delta w \) and \(\Delta b\)

(c) One Fourth Labs

\(\mathscr{L} = \frac{1}{2}(\hat{y} - y)^{2}\)

\(\frac{\partial \mathscr{L}}{\partial w_1} = \frac{\partial}{\partial w_1}(\frac{1}{2} [\hat{y} - y]^2)\)

\(\vdots\)

\(\frac{\partial \mathscr{L}}{\partial w_5} = \frac{\partial}{\partial w_5}(\frac{1}{2} [\hat{y} - y]^2)\)

\(\frac{\partial \mathscr{L}}{\partial w_2} = \frac{\partial}{\partial w_2}(\frac{1}{2} [\hat{y} - y]^2)\)

\(\Delta w_1 =(\hat{y} - y) * \hat{y}*(1- \hat{y}) *x_1 \)

\(\Delta w_2 =(\hat{y} - y) * \hat{y}*(1- \hat{y}) *x_2 \)

\(\Delta w_5 =(\hat{y} - y) * \hat{y}*(1- \hat{y}) *x_5 \)

\(\vdots\)

Learning Algorithm

How do I compute \(\Delta w \) and \(\Delta b\)

(c) One Fourth Labs

\(\begin{bmatrix} \Delta w_1 \\ \Delta w_2 \\ \vdots \\ \Delta w_5 \end{bmatrix} \)

\( \begin{bmatrix} (\hat{y}-y)*\hat{y}*(1-\hat{y})*x_1\\ (\hat{y}-y)*\hat{y}*(1-\hat{y})*x_2 \\ \vdots \\ (\hat{y}-y)*\hat{y}*(1-\hat{y})*x_5\end{bmatrix}\)

\( \Delta w \)

\( (\hat{y}-y)*\hat{y}*(1-\hat{y}) \begin{bmatrix} x_1 \\ x_2 \\ \vdots \\ x_5 \end{bmatrix} \)

Learning Algorithm

How does the full algorithm look like ?

(c) One Fourth Labs

How do you check the performance of the sigmoid model?

(c) One Fourth Labs

Evaluation

Launch (within 6 months)	0	1	1	0	0	1	0	1	1	0
Weight (<160g)	1	0	1	0	0	0	1	0	0	1
Screen size (<5.9 in)	1	0	1	0	1	0	1	0	1	0
dual sim	1	1	0	0	0	1	0	1	0	0
Internal memory (>= 64 GB, 4GB RAM)	1	1	1	1	1	1	1	1	1	0
NFC	0	1	1	0	1	0	1	1	1	0
Radio	1	0	0	1	1	1	0	0	0	0
Battery(>3500mAh)	0	0	0	1	0	1	0	1	0	0
Price > 20k	0	1	1	0	0	0	1	1	1	0
Like? (y)	1	1	1	0	0	1	1	1	0	0
predicted	1	1	0	1	1	1	1	0	0	0

1	0	0	1
0	1	1	1
0	1	1	1
0	1	0	0
1	0	0	0
0	0	1	0
1	1	1	0
1	1	1	0
0	0	1	0
0	1	0	0
0	1	1	0

Training data

Test data

Accuracy=\frac{\text{Number of correct predictions}}{\text{Total number of predictions}}

Accuracy=\frac{\text{Number of correct predictions}}{\text{Total number of predictions}}

= \frac{3}{4} = 75\%

= \frac{3}{4} = 75\%

Loss=\sum_{i=1}^{n} (y-\hat{y})^2

Loss=\sum_{i=1}^{n} (y-\hat{y})^2

y = \frac{1}{1 + e^{(-w^Tx+b)}}

y = \frac{1}{1 + e^{(-w^Tx+b)}}

Take-aways

What are the new things that we learned in this module ?

(c) One Fourth Labs

Show the 6 jars at the top (again can be small)

\( \{0, 1\} \)

\( \in \mathbb{R} \)

Tasks with Real inputs and real outputs

show the sigmoid plot with the issue of non-linearly separable data

show squared error loss

show gradient descent update rule

show accuracy formula

Take-aways

What are the new things that we learned in this module ?

(c) One Fourth Labs

A slide where we compare sigmoid, perceptron and MP neuron in terms of 6 jars

Still not complex enough to handle non-linear data