1.6 The Perceptron Model

Your first model with weights

Recap: MP Neuron

What did we see in the previous chapter?

(c) One Fourth Labs

Screen size (>5 in) 1 0 1 1 1 0 1 0 1 0
Battery (>2000mAh) 0 0 0 1 0 1 1 1 1 0
Like 1 0 1 0 1 1 0 1 0 0
\hat{y}
y^\hat{y}
x_1
x1x_1
x_2
x2x_2
b
bb
\hat{y}=\sum_{i=1}^n x_i \gt b
y^=∑i=1nxi>b\hat{y}=\sum_{i=1}^n x_i \gt b

Boolean inputs

Boolean output

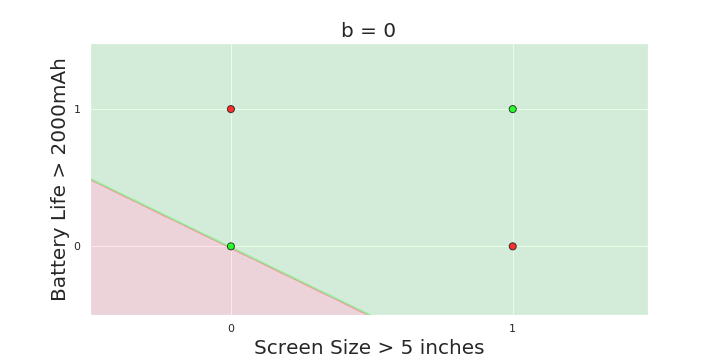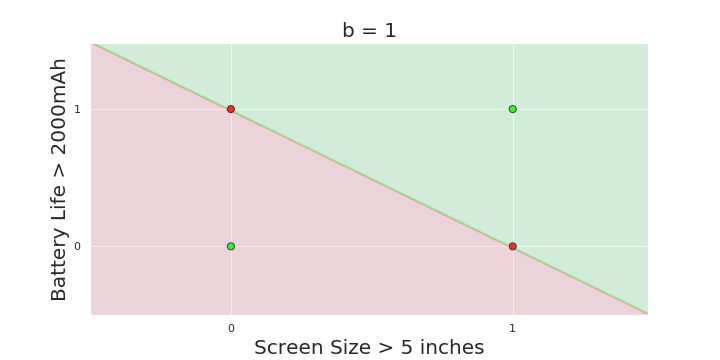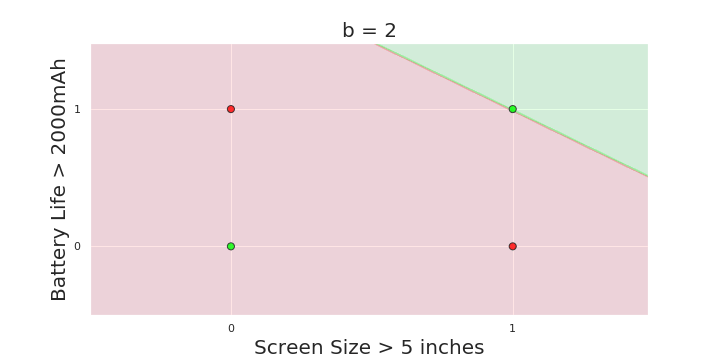
Linear

Fixed Slope

Few possible intercepts (b's)

The Road Ahead

What's going to change now ?

(c) One Fourth Labs

\( \{0, 1\} \)

Classification

loss = \sum_i (y_i-\hat{y_i})^2
loss=∑i(yi−yi^)2loss = \sum_i (y_i-\hat{y_i})^2
Accuracy=\frac{\text{Number of correct predictions}}{\text{Total number of predictions}}
Accuracy=Number of correct predictionsTotal number of predictionsAccuracy=\frac{\text{Number of correct predictions}}{\text{Total number of predictions}}

Loss

Model

Data

Task

Evaluation

Learning

Linear

Only one parameter, b

Real inputs

Boolean output

Brute force

Boolean inputs

loss = \sum_i max(0,1-y_i*\hat{y_i})
loss=∑imax(0,1−yi∗yi^)loss = \sum_i max(0,1-y_i*\hat{y_i})

Our 1st learning algorithm

Weights for every input

Data and Task

What kind of data and tasks can Perceptron process ?

(c) One Fourth Labs

Real inputs

Launch (within 6 months) 0 1 1 0 0 1 0 1 1
Weight (g) 151 180 160 205 162 182 138 185 170
Screen size (inches) 5.8 6.18 5.84 6.2 5.9 6.26 4.7 6.41 5.5
dual sim 1 1 0 0 0 1 0 1 0
Internal memory (>= 64 GB, 4GB RAM) 1 1 1 1 1 1 1 1 1
NFC 0 1 1 0 1 0 1 1 1
Radio 1 0 0 1 1 1 0 0 0
Battery(mAh) 3060 3500 3060 5000 3000 4000 1960 3700 3260
Price (INR) 15k 32k 25k 18k 14k 12k 35k 42k 44k
Like (y) 1 0 1 0 1 1 0 1 0
Launch (within 6 months) 0 1 1 0 0 1 0 1 1
Weight (<160g) 1 0 1 0 0 0 1 0 0
Screen size (<5.9 in) 1 0 1 0 1 0 1 0 1
dual sim 1 1 0 0 0 1 0 1 0
Internal memory (>= 64 GB, 4GB RAM) 1 1 1 1 1 1 1 1 1
NFC 0 1 1 0 1 0 1 1 1
Radio 1 0 0 1 1 1 0 0 0
Battery(>3500mAh) 0 0 0 1 0 1 0 1 0
Price > 20k 0 1 1 0 0 0 1 1 1
Like (y) 1 0 1 0 1 1 0 1 0

(c) One Fourth Labs

Launch (within 6 months) 0 1 1 0 0 1 0 1 1
Weight (g) 151 180 160 205 162 182 138 185 170
Screen size (inches) 5.8 6.18 5.84 6.2 5.9 6.26 4.7 6.41 5.5
dual sim 1 1 0 0 0 1 0 1 0
Internal memory (>= 64 GB, 4GB RAM) 1 1 1 1 1 1 1 1 1
NFC 0 1 1 0 1 0 1 1 1
Radio 1 0 0 1 1 1 0 0 0
Battery(mAh) 3060 3500 3060 5000 3000 4000 1960 3700 3260
Price (INR) 15k 32k 25k 18k 14k 12k 35k 42k 44k
Like (y) 1 0 1 0 1 1 0 1 0
screen size
5.8
6.18
5.84
6.2
5.9
6.26
4.7
6.41
5.5
screen size
0.64
0.87
0.67
0.88
0.7
0.91
0
1
0.47

min

max

Standardization formula

x' = \frac{x-min}{max-min}
x′=x−minmax−minx&#x27; = \frac{x-min}{max-min}
Launch (within 6 months) 0 1 1 0 0 1 0 1 1
Weight (g) 151 180 160 205 162 182 138 185 170
Screen size 0.64 0.87 0.67 0.88 0.7 0.91 0 1 0.47
dual sim 1 1 0 0 0 1 0 1 0
Internal memory (>= 64 GB, 4GB RAM) 1 1 1 1 1 1 1 1 1
NFC 0 1 1 0 1 0 1 1 1
Radio 1 0 0 1 1 1 0 0 0
Battery(mAh) 3060 3500 3060 5000 3000 4000 1960 3700 3260
Price (INR) 15k 32k 25k 18k 14k 12k 35k 42k 44k
Like (y) 1 0 1 0 1 1 0 1 0
battery
3060
3500
3060
5000
3000
4000
1960
3700
3260
battery
0.36
0.51
0.36
1
0.34
0.67
0
0.57
0.43

min

max

Data Preparation

Can the data be used as it is ?

Launch (within 6 months) 0 1 1 0 0 1 0 1 1
Weight (g) 151 180 160 205 162 182 138 185 170
Screen size 0.64 0.87 0.67 0.88 0.7 0.91 0 1 0.47
dual sim 1 1 0 0 0 1 0 1 0
Internal memory (>= 64 GB, 4GB RAM) 1 1 1 1 1 1 1 1 1
NFC 0 1 1 0 1 0 1 1 1
Radio 1 0 0 1 1 1 0 0 0
Battery 0.36 0.51 0.36 1 0.34 0.67 0 0.57 0.43
Price (INR) 15k 32k 25k 18k 14k 12k 35k 42k 44k
Like (y) 1 0 1 0 1 1 0 1 0

Data Preparation

Can the data be used as it is ?

(c) One Fourth Labs

Launch (within 6 months) 0 1 1 0 0 1 0 1 1
Weight 0.19 0.63 0.33 1 0.36 0.66 0 0.70 0.48
Screen size 0.64 0.87 0.67 0.88 0.7 0.91 0 1 0.47
dual sim 1 1 0 0 0 1 0 1 0
Internal memory (>= 64 GB, 4GB RAM) 1 1 1 1 1 1 1 1 1
NFC 0 1 1 0 1 0 1 1 1
Radio 1 0 0 1 1 1 0 0 0
Battery 0.36 0.51 0.36 1 0.34 0.67 0 0.57 0.43
Price 0.09 0.63 0.41 0.19 0.06 0 0.72 0.94 1
Like (y) 1 0 1 0 1 1 0 1 0

The Model

What is the mathematical model ?

(c) One Fourth Labs

Launch (within 6 months) 0 1 1 0 0 1 0 1 1
Weight 0.19 0.63 0.33 1 0.36 0.66 0 0.70 0.48
Screen size 0.64 0.87 0.67 0.88 0.7 0.91 0 1 0.47
dual sim 1 1 0 0 0 1 0 1 0
Internal memory (>= 64 GB, 4GB RAM) 1 1 1 1 1 1 1 1 1
NFC 0 1 1 0 1 0 1 1 1
Radio 1 0 0 1 1 1 0 0 0
Battery 0.36 0.51 0.36 1 0.34 0.67 0 0.57 0.43
Price 0.09 0.63 0.41 0.19 0.06 0 0.72 0.94 1
Like (y) 1 0 1 0 1 1 0 1 0

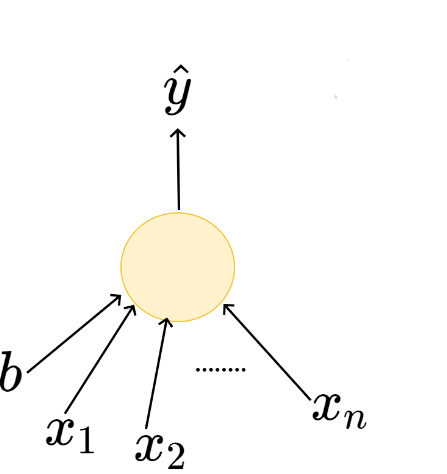
\(x_1\)

b

\(x_n\)

\(\hat{y}\)

\(x_2\)

\(w_1\)

\(w_2\)

\(w_n\)

\hat{y} = 1 \text{ if } \sum_{i=1}^n w_i x_i \geq b
y^=1 if ∑i=1nwixi≥b\hat{y} = 1 \text{ if } \sum_{i=1}^n w_i x_i \geq b
\hat{y} = 0 \text{ otherwise }
y^=0 otherwise \hat{y} = 0 \text{ otherwise }

The Model

How is this different from the MP Neuron Model ?

(c) One Fourth Labs

Real inputs

Linear

Weights for each input

Adjustable threshold

Boolean inputs

Linear

Inputs are not weighted

Adjustable threshold

\hat{y} = 1 \text{ if } \sum_{i=1}^n w_i x_i \geq b
y^=1 if ∑i=1nwixi≥b\hat{y} = 1 \text{ if } \sum_{i=1}^n w_i x_i \geq b
\hat{y} = 0 \text{ otherwise }
y^=0 otherwise \hat{y} = 0 \text{ otherwise }
\hat{y} = 1 \text{ if } \sum_{i=1}^n x_i \geq b
y^=1 if ∑i=1nxi≥b\hat{y} = 1 \text{ if } \sum_{i=1}^n x_i \geq b
\hat{y} = 0 \text{ otherwise }
y^=0 otherwise \hat{y} = 0 \text{ otherwise }

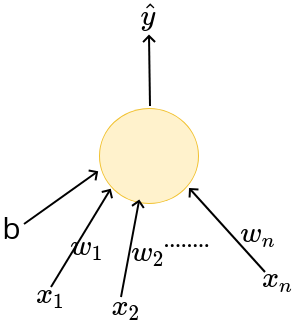
MP Neuron 

Perceptron

The Model

What do weights allow us to do ?

(c) One Fourth Labs

Launch (within 6 months) 0 1 1 0 0 1 0 1 1
Weight (g) 151 180 160 205 162 182 158 185 170
Screen size (inches) 5.8 6.18 5.84 6.2 5.9 6.26 5.7 6.41 5.5
dual sim 1 1 0 0 0 1 0 1 0
Internal memory (>= 64 GB, 4GB RAM) 1 1 1 1 1 1 1 1 1
NFC 0 1 1 0 1 0 1 1 1
Radio 1 0 0 1 1 1 0 0 0
Battery(mAh) 3060 3500 3060 5000 3000 4000 2960 3700 3260
Price (INR) 15k 32k 25k 18k 14k 12k 35k 42k 44k
Like (y) 1 0 1 0 1 1 0 1 0

\(x_1\)

b

\(x_n\)

\(\hat{y}\)

\(x_2\)

\(w_1\)

\(w_2\)

\(w_n\)

\(w_{price} \rightarrow -ve\)

Like  \(\alpha  \frac{1}{price}\)

\hat{y} = 1 \text{ if } \sum_{i=1}^n w_i x_i \geq b
y^=1 if ∑i=1nwixi≥b\hat{y} = 1 \text{ if } \sum_{i=1}^n w_i x_i \geq b
\hat{y} = 0 \text{ otherwise }
y^=0 otherwise \hat{y} = 0 \text{ otherwise }

Some Math fundae

Can we write the perceptron model slightly more compactly?

(c) One Fourth Labs

x : [0, 0.19, 0.64, 1, 1, 0]

w: [0.3, 0.4, -0.3, 0.1, 0.5]

 \(\textbf{x} \in R^5\)

 \(\textbf{w} \in R^5\)

\( \vec{x} \)

\( \vec{w} \)

\(\textbf{x}.\textbf{w}\) = ?

\(\textbf{x}.\textbf{w} = x_1.w_1 + x_2.w_2 + ... x_n.w_n\)

= \sum_{i=1}^n x_i.w_i
=∑i=1nxi.wi= \sum_{i=1}^n x_i.w_i
\hat{y}= 1 \text{ (if } \textbf{x}.\textbf{w} \geq b)
y^=1 (if x.w≥b)\hat{y}= 1 \text{ (if } \textbf{x}.\textbf{w} \geq b)
\hat{y}= 0 \text{ (otherwise)}
y^=0 (otherwise)\hat{y}= 0 \text{ (otherwise)}

\(x_1\)

b

\(x_n\)

\(\hat{y}\)

\(x_2\)

\(w_1\)

\(w_2\)

\(w_n\)

\( \textbf{x} \)

\( \textbf{w} \)

\hat{y} = 1 \text{ if } \sum_{i=1}^n w_i x_i \geq b
y^=1 if ∑i=1nwixi≥b\hat{y} = 1 \text{ if } \sum_{i=1}^n w_i x_i \geq b
\hat{y} = 0 \text{ otherwise }
y^=0 otherwise \hat{y} = 0 \text{ otherwise }

\(\textbf{x}.\textbf{w} \)

= \sum_{i=1}^n x_i.w_i
=∑i=1nxi.wi= \sum_{i=1}^n x_i.w_i

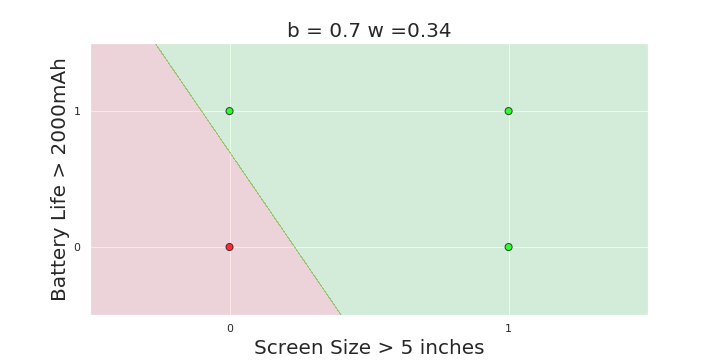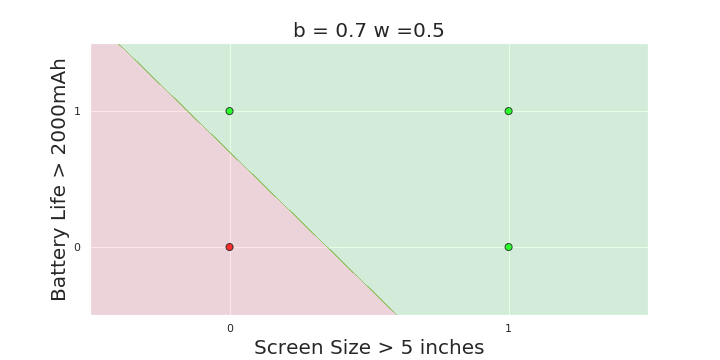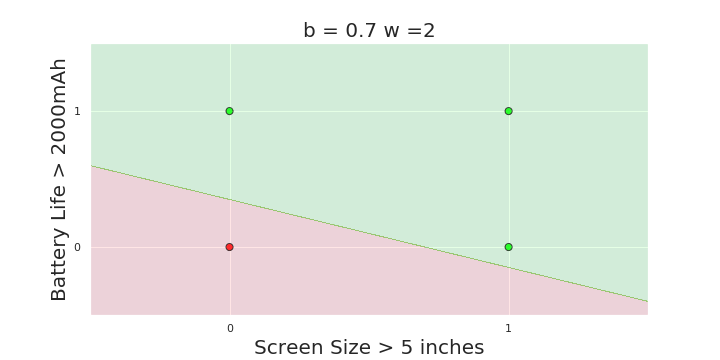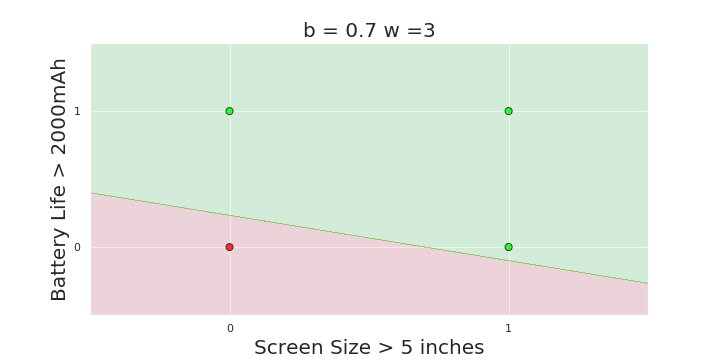
The Model

What is the geometric interpretation of the model ?

(c) One Fourth Labs

More freedom

MP neuron

Perceptron

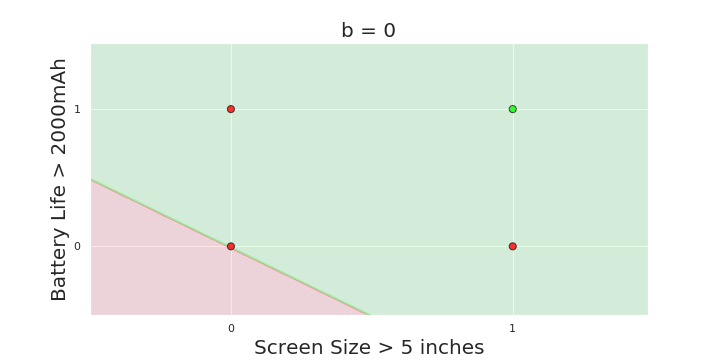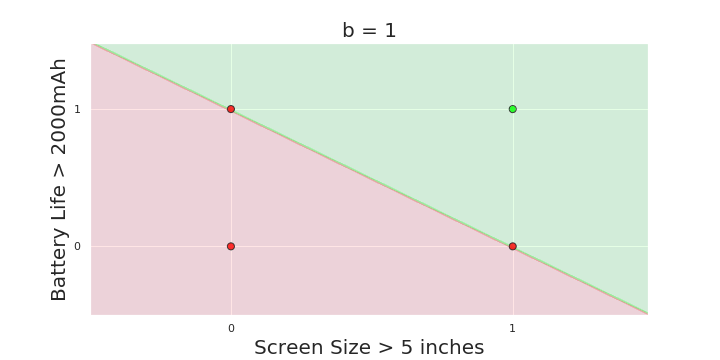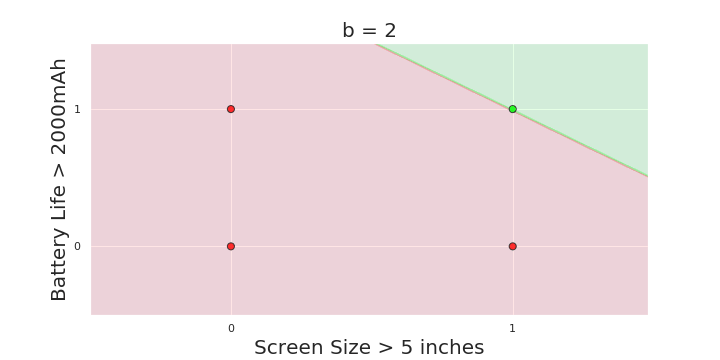
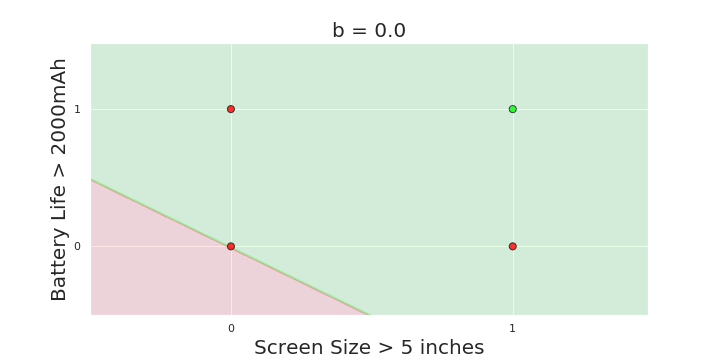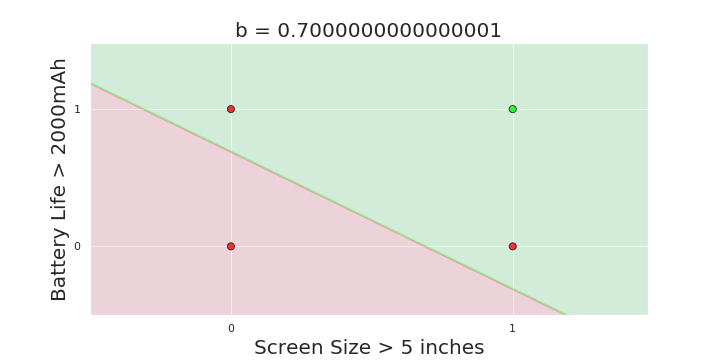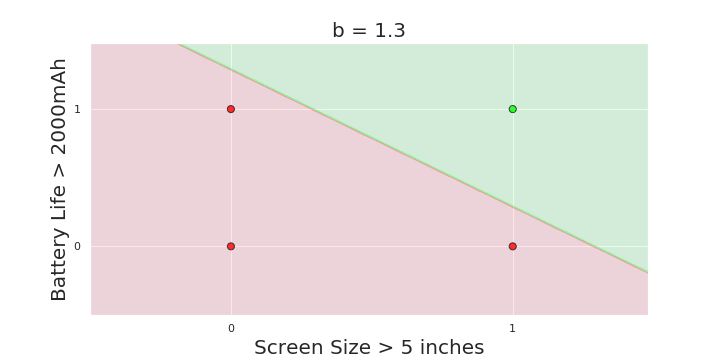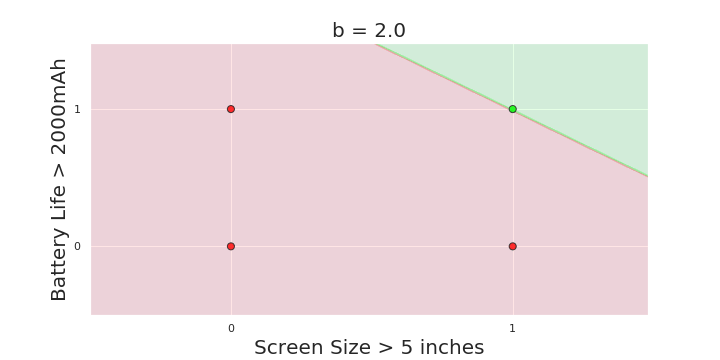
The Model

Why is more freedom important ?

(c) One Fourth Labs

More freedom

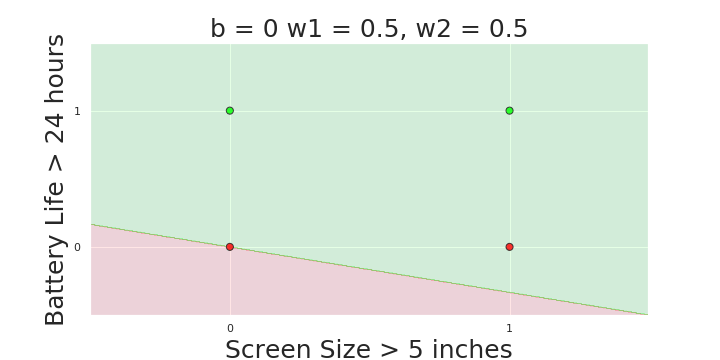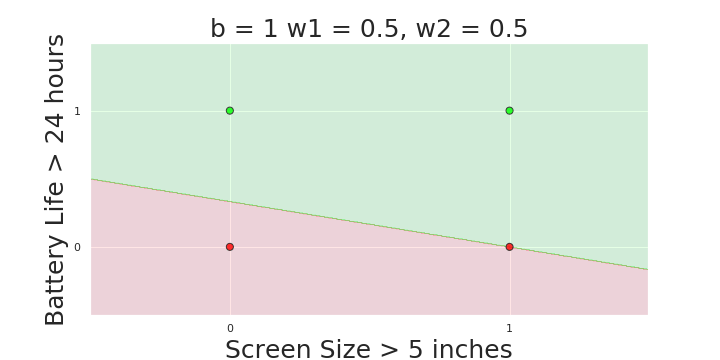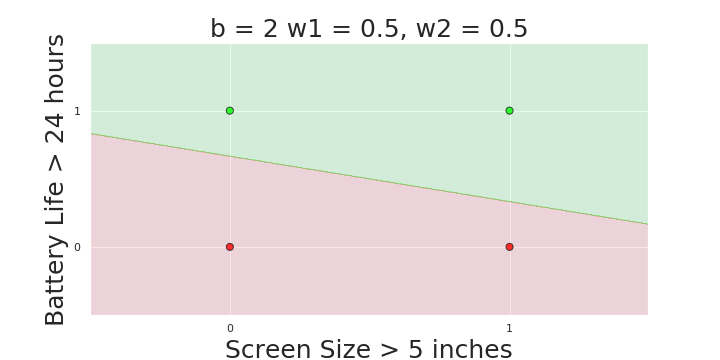
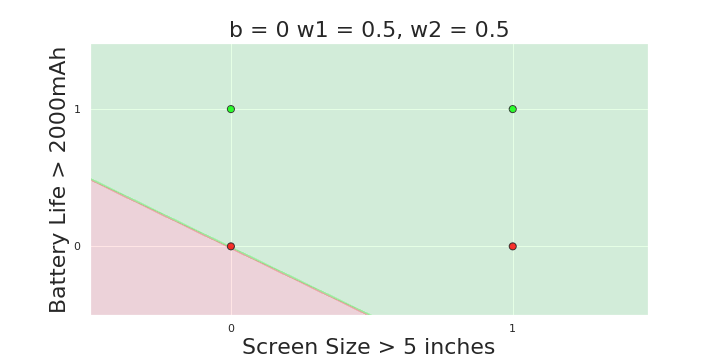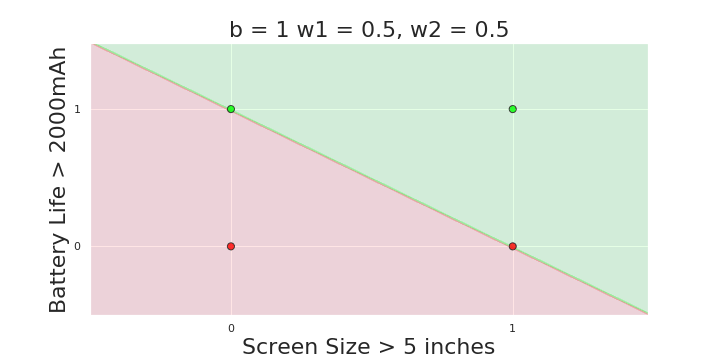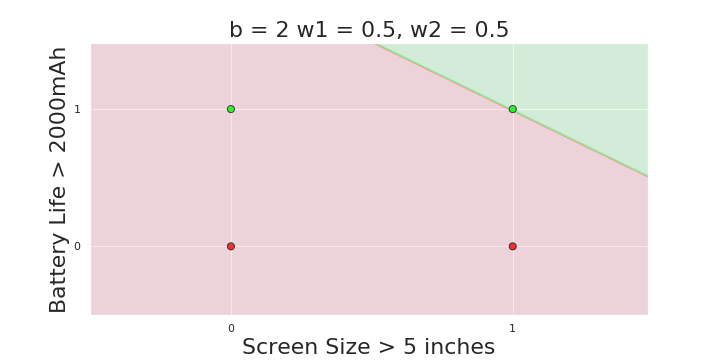
MP neuron

Perceptron

The Model

Is this all the freedom that we need ?

(c) One Fourth Labs

We want even more freedom

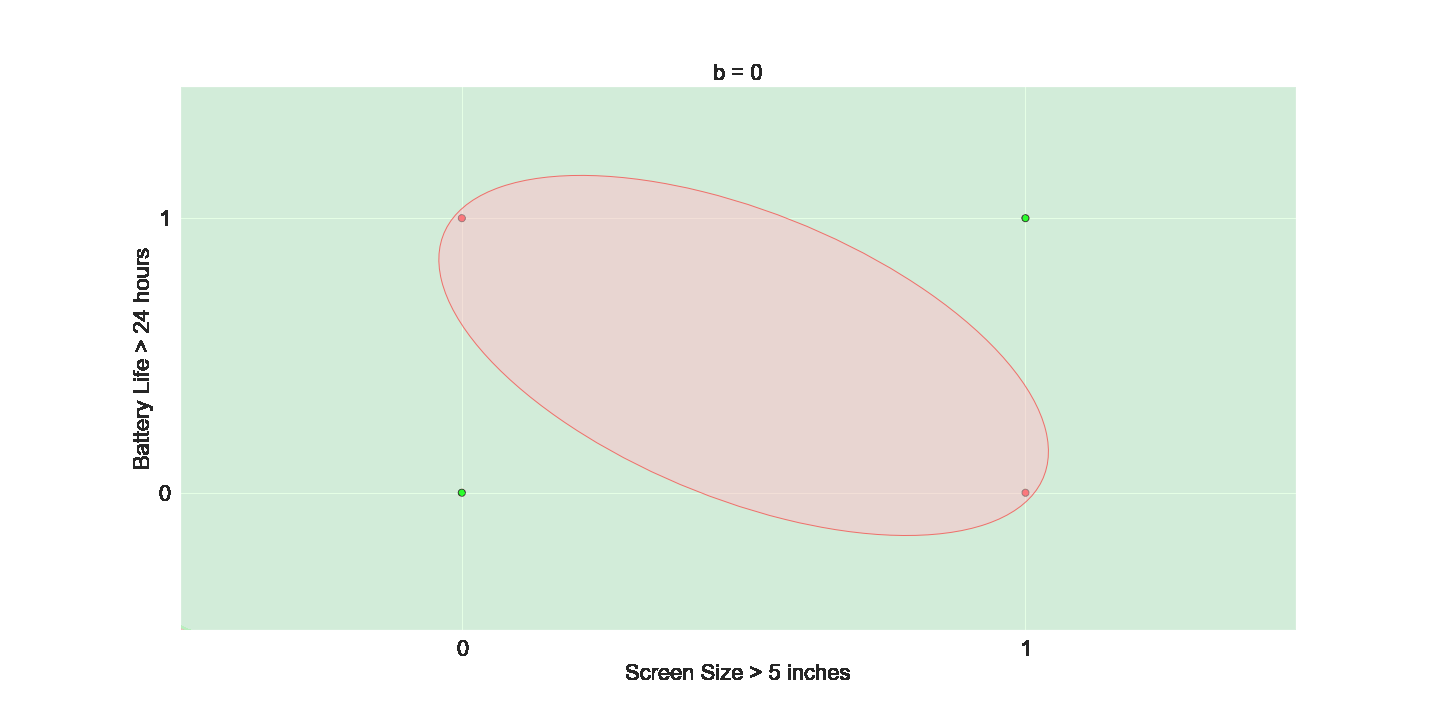
The Model

What if we have more than 2 dimensions ?

(c) One Fourth Labs

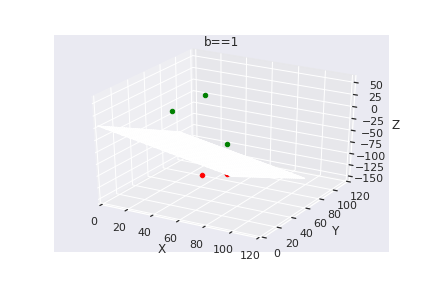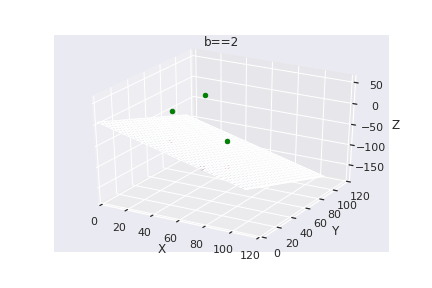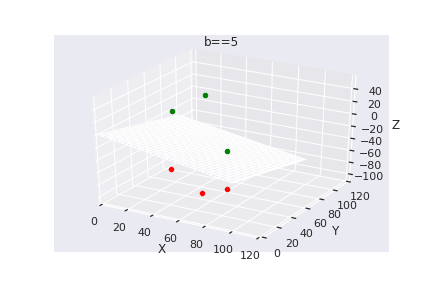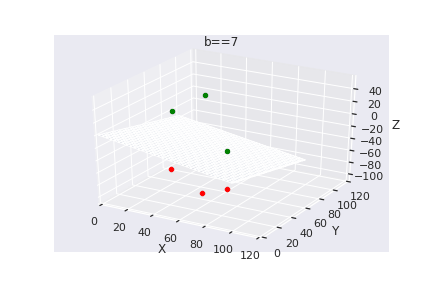
Loss Function

What is the loss function that you use for this model ?

(c) One Fourth Labs

First write it as this,

L = 0 if y = \hat{y}

   = 1 if y != \hat{y} 

 

Now write it more compactly as 

\indicator_{y - \hat{y}}

1. Show small training matrix here

2. Show the loss function as if-else

3. Show the loss function as indicator variable

4. Now add a column for y_hat and compute the loss

5. Now show the pink box with the QA

 

Q. What is the purpose of the loss function ?

A. To tell the model that some correction needs to be done!

Q. How ?

A. We will see soon

Loss Function

How is this different from the squared error loss function ?

(c) One Fourth Labs

First write it as this,

L = 0 if y = \hat{y}

   = 1 if y != \hat{y} 

 

Now write it more compactly as 

\indicator_{y - \hat{y}}

1. Show small training matrix here

2. Show the loss function as if-else

3. Show the loss function as indicator variable

4. Now add a column for y_hat and compute the loss

5. Now show the pink box with the QA

 

Q. What is the purpose of the loss function ?

A. To tell the model that some correction needs to be done!

Q. How ?

A. We will see soon

Loss Function

How is this different from the squared error loss function ?

(c) One Fourth Labs

1.

Show small training matrix here

Show output of model

2. squared error loss and perceptron loss formula on LHS

3. Add two columns to compute these losses one row at a time the QA

4 Show the pink box

 

 

Squared error loss is equivalent to perceptron loss when the outputs are boolean

Loss Function

Can we plot the loss function ?

(c) One Fourth Labs

- Show single variable data on LHS so that there are only two parameters w,b 

- Show model below it

- Now show a 3d-plot with w,b,error

- Substitute different values of w,b and compute output (additional column in the matrix) and loss (additional column in the matrix)

- Show how the error changes as you change the value of w,b

 

Learning Algorithm

 

What is the typical recipe for learning parameters of a model ?

(c) One Fourth Labs

Initialise 

1. Show training matrix with 2 inouts and one output

 

2. on LHS show the box containing w1, w2, b

 

3. Initialize

 

4. Iterate over data

 

5. Highlight first row in data

 

6. compute_loss

7. update

8 now highlight iterate over data

9. highlight second row, third row, ..., come back to first row

10. till satisfied

11. replace w1, w2 by w and show the box below

 

\(w_1, w_2, b \)

Iterate over data:

\( \mathscr{L}  = compute\_loss(x_i) \)

\( update(w_1, w_2, b, \mathscr{L}) \)

till satisfied

\(\mathbf{w} = [w_1, w_2] \)

Learning Algorithm

 

What does the perceptron learning algorithm look like ?

Show the algorithm here, use similar animations as in my lecture. I don't think you can use \algorithmic here

Instead of defining P and N, you can just rewrite the "if" condition as "if y_i = 1 and wx < 0"

 

w = w + x

b = b + 1

Show the model equation here

 

First in summation form and then in vector form

 

Show that the input x is also a vector

 

 

(c) One Fourth Labs

Learning Algorithm

 

Can we see this algorithm in action ?

(c) One Fourth Labs

Show the data here

 

Add a column for wx+b

and a column for y_hat

Show the algorithm here

Show a 3d plot here of how the values of w1,w2 and b change and the positive and negative half space changes as you go over each data point

 

 

Learning Algorithm

 

What is the geometric interpretation of this ?

(c) One Fourth Labs

- Show model equations again

- Now show the plot and the animations suggested in the black box on the RHS

 

 

Now show a plot containing only w and b

 

show what happens when we do b = b + 1. (The line shifts towards the point)

 

show what happens when we do w = w + x

(the line rotates towards the point)

 

Repeat the same for a negative point and show that the opposite happens

 

Learning Algorithm

 

What is the geometric interpretation of this (in higher dimensions) ?

(c) One Fourth Labs

- Show model equations again

- Now drop b from the equation

- wx = 0 is a plane which separates the input space into two halves (show plane in the plot)

- Every point x on this plane satisfies the equation wx = 0 (show a plane and points on this plane as vectors)

- w is perpendicular to this plane (show w vector perpendicular to all the points and hence the plane )

- Now show a point in the positive half space as a vector

- Show angle \alpha between this vector and the w vector

- below this box \alpha < 90 --> cos \alpha <0 --> wx < 0

 

- repeat the above for a negative point

 

Plot here

Learning Algorithm

 

How does adding/subtracting x to/from w help ?

(c) One Fourth Labs

Highlight a negative point which was misclassified (you will have to show that it lies on the other side of the plane)

 

cos(\aplha) = wx < 0

 

w_new = w - x

cos(\apha_new) = ...now the derivation from my lecture slides

 

 

now show that the plane indeed rotates so that the point moves closer to the negative half space (there is a continuation on the next slide)

 

Plot here

Learning Algorithm

 

How does adding/subtracting 1 from b help ?

(c) One Fourth Labs

b = b - 1

 

the plane will move down now so that the point will go to the other side

Plot here

Learning Algorithm

 

Will this algorithm always work ?

(c) One Fourth Labs

Show a plot of linearly separable data (similar to that in my lecture slides)

 

Now draw a line which separates the points

Show a plot of linearly separable data (similar to that in my lecture slides)

 

Now draw a line which separates the points

Only if the data is linearly separable

Learning Algorithm

 

Can we prove that it will always work for linearly separable data ?

(c) One Fourth Labs

Show a plot of linearly separable data (similar to that in my lecture slides)

 

Now draw a line which separates the points

Put the statement of the proof here

Learning Algorithm

 

What does "till satisfied" mean ?

(c) One Fourth Labs

Initialise 

\(w_1, w_2, b \)

Iterate over data:

\( \mathscr{L}  = compute\_loss(x_i) \)

\( update(w_1, w_2, b, \mathscr{L}) \)

till satisfied

\( total\_loss  = 0 \)

\( total\_loss  += \mathscr{L} \)

till total loss becomes 0

till total loss becomes < \( \epsilon \)

till number of iterations exceeds k (say 100)

Evaluation

 

How do you check the performance of the perceptron model?

(c) One Fourth Labs

Same slide as that in MP neuron

Take-aways

So will you use MP neuron?

(c) One Fourth Labs

 

\( \in \mathbb{R} \)

Classification

loss = \sum_i (y_i-\hat{y_i})^2
loss=∑i(yi−yi^)2loss = \sum_i (y_i-\hat{y_i})^2
Accuracy=\frac{\text{Number of correct predictions}}{\text{Total number of predictions}}
Accuracy=Number of correct predictionsTotal number of predictionsAccuracy=\frac{\text{Number of correct predictions}}{\text{Total number of predictions}}

Loss

Model

Data

Task

Evaluation

Learning

Real inputs

Boolean Output

An Eye on the Capstone project

How is perceptron related to the capstone project ?

(c) One Fourth Labs

Show the 6 jars at the top (again can be small)

 

\( \{0, 1\} \)

\( \in \mathbb{R} \)

 

Show that the signboard image can be represented as real numbers

Boolean

 

text/no-text

Show a plot with all text images on one side and non-text on another

show squared error loss

show perceptronlearning algorithm

show accuracy formula

and show a small matrix below with some ticks and crossed and show how accuracy will be calculated

The simplest model for binary classification

An Eye on the Capstone project

How is perceptron related to the capstone project ?

(c) One Fourth Labs

Show the 6 jars at the top (again can be small)

 

\( \{0, 1\} \)

\( \in \mathbb{R} \)

 

Show that the signboard image can be represented as real numbers

Boolean

 

text/no-text

Show a plot with all text images on one side and non-text on another

show squared error loss

show perceptronlearning algorithm

show accuracy formula

and show a small matrix below with some ticks and crossed and show how accuracy will be calculated

The simplest model for binary classification

\( \{0, 1\} \)

Boolean

loss = \sum_i (y_i-\hat{y_i})^2
loss=∑i(yi−yi^)2loss = \sum_i (y_i-\hat{y_i})^2
Accuracy=\frac{\text{Number of correct predictions}}{\text{Total number of predictions}}
Accuracy=Number of correct predictionsTotal number of predictionsAccuracy=\frac{\text{Number of correct predictions}}{\text{Total number of predictions}}

Loss

Model

Data

Task

Evaluation

Learning

Linear

Only one parameter, b

Real inputs

Boolean output

Brute force

Boolean inputs

loss = \sum_i max(0,1-y_i*\hat{y_i})
loss=∑imax(0,1−yi∗yi^)loss = \sum_i max(0,1-y_i*\hat{y_i})

Our 1st learning algorithm

Weights for every input

Assignments

 

How do you view the learning process ?

(c) One Fourth Labs

Assignment: Give some data including negative values and ask them to standardize it

Made with Slides.com