C++基礎語法

內容：函式、遞迴、結構

佛倫斯

你是否有遇過以下問題？

哭阿同個功能的東西一直重複寫
整個扣都很凌亂
好想像python一樣好多方便的函式……

Function saves the day!

gcd(a,b)：回傳a和b的最大公因數
lcm(a,b)：回傳a和b的最小公倍數
swap(a,b)：交換a和b
max(a,b)：回傳a或b較大的那個
min(a,b)：回傳a或b較小的那個
abs(n)：回傳絕對值n

其實還有很多⋯⋯

C++函式庫

type function_name(parameters) {
  // 程式碼
  return variable;
}

type：function會回傳什麼型態的變數

function_name：function的名字

parameters：function的參數

return：function結束並回傳變數

＊使用前先宣告！

函式（Function）

int plus_one(int number) {
  return number + 1;
}

type：回傳一個整數

function_name：命名為plus_one

parameters：傳入一個整數number

return：function結束並回傳number+1

Return Type

int a = 3, b = 5;
swap(a, b); //交換a,b兩數
cout << a << ' ' << b << "\n";

可以做為變數的都可以當回傳值…

但如果沒有回傳任何東西呢？

Return Type

void print_hello() {
  cout << "hello\n";
}

「void」只能做為return type，

不能作為變數型別

void沒有回傳變數，連return都可以省略

owo

參數

預設參數（Default Parameters）

可傳可不傳ㄉ參數

int multiply(int a, int b = 2){
    return a*b;
}
int num1 = multiply(3);
int num2 = multiply(3,2);
// num1 = num2

預設的參數一定要放最後面！

Return

函式結束並回傳

當function type不是void時，就需要return

return的用處：

結束function的執行
回傳數值給呼叫者

Return

int divide(int a,int b){
    if(b == 0){
        return -1;
    }
    /* 沒必要加else，因為如果b是0，
       return後函式就結束了 */
    return a/b;
}

結束function的執行

void也可以return喔！

（只是沒有return值，直接 return;）

Return

int add(int a,int b){
    return a+b;
}
int num = add(1,2);
cout<<num<<endl;
//num = 3

回傳數值給呼叫者

void也可以return喔！

（只是沒有return值，直接 return;）

Return

int formula(int a,int b,int c){
    //solve....
    return x1,x2;
}

回傳數值給呼叫者

同時回傳兩個以上的數值?

例：一元二次方程式 \(ax^2+bx+c=0, a\neq 0\)

不能這樣做！！！

想要回傳多個值？

std::pair
std::tuple
struct

其中一個等等會教，其他的之後STL會教！

void f(int x) {
    cout << x*x << '\n';
}

bool g(int y, int z=9) {
    if ((y+z)%4 != 0)  return false;
    return true;
}

int main() {
    f(5); // 輸出5*5 = "25"
    if (g(3) && g(4, 12))
        cout << " true\n";
    // 輸出g(3,9)&&g(4,12) = true
    // 4|(3+9)且4|(4+12)
    else    cout << '\n';
    // 輸出：25 true
}

遞迴

\(a_1 = 1\)

\(a_{n+1} = 3 a_n+2\)

\(a_{n+1}+1 = 3a_n+3 = 3(a_n+1)\)

\(a_2+1 = 3(a_1+1)\)

\(a_3+1 = 3(a_2+1)\)

\(\vdots\)

\(a_n+1 = 3(a_{n-1}+1)\)

上面\(n-1\)條等式全部相乘

\(\Rightarrow a_n+1 = 3^{n-1}(a_1+1)\)

\(\Rightarrow a_n=3^{n-1}\cdot 2-1\)

\(a_1 = 1\)

\(a_{n+1} = 3 a_n+2\)

int a(int n) {
    if (n == 1) {
        return 1;
    }
    return 3*a(n-1)+2;
}

\(a(n)\)是\(n\)的函數，\(a(n)=\begin{cases}1,\ n=1\\3\cdot a(n-1)+2,\ n\geq 2\end{cases}\ \ n\in\mathbb{N}\)

\(a(n-1) = 3\cdot a(n-2) + 2\)

\(\Rightarrow a(n) = 3\cdot (3\cdot a(n-2)+2)+2\)

\(\Rightarrow a(n) = 3\cdot [3\cdot (3\cdot a(n-3)+2)+2]+2\)

\(\vdots\)

斐波那契數列

\(a_n = \begin{cases}1,\ n=1,2\\a_{n-1}+a_{n-2},\ n\geq 3\end{cases}\ \ n\in \mathbb{N}\)

特徵方程式：\(x^2 = x+1,\ x = \frac{1\pm \sqrt 5}{2}\)

\(a_n = A\cdot \left(\frac{1+\sqrt{5}}{2}\right)^{n} + B\cdot \left(\frac{1-\sqrt{5}}{2}\right)^{n}\)

n代1、2，解A、B

\(a_1 = 1 = A\cdot \left(\frac{1+\sqrt{5}}{2}\right)^1+B\cdot\left(\frac{1-\sqrt{5}}{2}\right)^1\)

\(a_2 = 1 = A\cdot \left(\frac{1+\sqrt{5}}{2}\right)^2 + B\cdot \left(\frac{1-\sqrt{5}}{2}\right)^2\)

\(A=\frac{1}{\sqrt{5}},\ B=\frac{-1}{\sqrt{5}}\)

\(\Rightarrow a_n = \frac{1}{\sqrt{5}}\left[\left(\frac{1+\sqrt{5}}{2}\right)^n-\left(\frac{1-\sqrt{5}}{2}\right)^n\right]\)

int f(int n) {
    if (n == 1) return 1;
    else if (n == 2) return 1;
    else return f(n-1)+f(n-2);
}

\(f(n)=\begin{cases}1,\ n=1, 2\\f(n-1)+f(n-2),\ n\geq 3\end{cases}\)

結構（Struct）

struct struct_name{
    int a;
    string b;
    float c;
}; // 注意這裡要分號

struct是使用者自訂的型態（像int, bool都是型態）

struct_name：struct的名字

2~4行：struct的成員

最後面一定要加分號「;」

struct coor{
    float x, y;
};

float distance(coor c1, coor c2) {
    return sqrt((c1.x-c2.x)*(c1.x-c2.x)
        +(c1.y-c2.y)*(c1.y-c2.y));
    // sqrt()：開根號
    // 存取資料成員：
    // 變數名稱.資料成員名稱
}

座標上存兩個點\(c_1(x_1, y_1),\ c_2(x_2,y_2)\)

算兩點距離：\(d=\sqrt{(x_1-x_2)^2 + (y_1-y_2)^2}\)

\(x_1=c_1.x, x_2=c_2.x,y_1=c_1.y,y_2=c_2.y\)

實作

題目

ZJ e156：良心題：求和
ZJ e357：遞迴函數練習
ZJ c002：10696 - f91
ZJ a006：一元二次方程式
ZJ a042：平面圓形切割
ZJ d389：11069 - A Graph Problem

ZJ e156：良心題：求和

輸入一個正整數\(n\ (1\leq n\leq 1000)\)，

輸出\(1+2+\dots+n\)

範例輸入：3

範例輸出：6 （1+2+3 = 6）

ZJ e357：遞迴函數練習

定義一函數\(F(x)\)，

\(F(x)=\begin{cases}1,\ \ x=1\\F \left(\frac{x}{2}\right),\ \ 2|x\\F(x-1)+F(x+1),\ \ x=3, 5, 7, \dots\end{cases}\)

輸入一正整數x，輸出F(x)

範例輸入：6 範例輸出：2

\(F(6)=F(3)=F(4)+F(2)=F(2)+F(1)\\=1+F(1)=2\)

ZJ c002：10696 - f91

\(f91(N)=\begin{cases}f91(f91(N+11)),\ \ N\leq 100\\N-10,\ \ N\geq 101\end{cases}\)

範例輸入：500

範例輸出：490

\(f91(500)=500-10\\=490\)

範例輸出：91

ZJ a006：一元二次方程式

求一元二次方程式\(ax^2+bx+c=0,\ a\neq 0\)的根

每組輸入共一行，內含三個整數 a, b, c 以空白隔開

兩相異根：Two different roots x1=？ , x2=？
兩重根：Two same roots x=？
無實數根：No real root

PS：答案均為整數，若有兩個根則大者在前

解\(ax^2+bx+c=0\)

令\(D=b^2-4ac\)

\(D\geq 0:x=\frac{-b\pm \sqrt D}{2a}\)

\(D<0: x\)無實數解

#include <cmath>
// 使用根號要#include <cmath>

// sqrt(9) = 3

範例輸入1：1 3 -10

範例輸入2：1 0 0

範例輸入3：1 1 1

範例輸出1：Two different roots x1=2 , x2=-5

範例輸出2：Two same roots x=0

範例輸出3：No real root

ZJ a042：平面圖形切割

對任意正整數n，平面上的n個圓最多可將平面切成幾個區域？

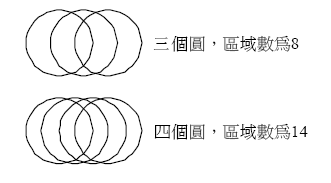
測試資料中有多筆測資，每個測資一列，每列含一數字\(n\ (1\leq n\leq 76)\)，讀到測資讀完為止（EOF）

int n; // 先宣告
while (cin >> n) {
    // 遇到要讀到檔案結束的題目，用while(cin >> n)
}

範例輸入：1

範例輸出：2（圓內、圓外）

ZJ d389：11069 - A Graph Problem

給一個有\(n\ (1\leq n\leq 76)\)個節點的圖形

測試資料中有多筆測資，每個測資一列，每列含一數字\(n\ (1\leq n\leq 76)\)，讀到測資讀完為止（EOF）

int n; // 先宣告
while (cin >> n) {
    // 遇到要讀到檔案結束的題目，用while(cin >> n)
}

範例輸入：5

範例輸出：4

n = 5所有合法的集合：{1,3,5}, {2,4}, {2,5}, {1,4}

題解

ZJ e156：良心題：求和

#include <iostream>
using namespace std;

int main() {
    int n;  cin >> n;
    cout << n*(n+1)/2 << '\n';
}

\( \sum \limits ^{n}_{x=1} x=\frac{n(n+1)}{2}\)

\(S_n=\frac{[2a_{1}+(n-1)d]n}{2}\)

ZJ e156：良心題：求和

#include <iostream>
using namespace std;

int f(int n) {
    if (n == 1)
	return 1;
    return n+f(n-1);
}

int main() {
    int x;   cin >> x;
    cout << f(x) << '\n';
}

\(a_n = \begin{cases}1\ \ \ (n=1)\\a_{n-1}+n\ \ \ (n\geq 2)\end{cases}\)

ZJ e357：遞迴函數練習

#include <iostream>
using namespace std;

int F(int x) {
    if (x == 1)     return 1;
    if (x%2 == 0)   return F(x/2);
    return F(x+1)+F(x-1);
}

int main() {
    int x;  cin >> x;
    cout << F(x) << '\n';
}

\(F(x)=\begin{cases}1,\ \ x=1\\F \left(\frac{x}{2}\right),\ \ 2|x\\F(x-1)+F(x+1),\ \ x=3, 5, 7, \dots\end{cases}\)

ZJ c002：10696 - f91

#include <iostream>
using namespace std;

int f91(int N) {
    if (N >= 101)   return N-10;
    if (N <= 100)   return f91(f91(N+11));
}

int main() {
    int N;
    while (true) {
        cin >> N;
        if (N == 0) break;
        cout << "f91(" << N << ") = "
             << f91(N) << '\n';
    }
}

\(f91(N)=\begin{cases}f91(f91(N+11)),\ \ N\leq 100\\N-10,\ \ N\geq 101\end{cases}\)

ZJ a006：一元二次方程式

#include <iostream>
#include <cmath>
using namespace std;

struct roots{
    int x1, x2;
};

roots solve(int a, int b, int c) {
    roots r;    int x1, x2;
    x1 = (-b+sqrt(b*b-4*a*c))/(2*a);
    x2 = (-b-sqrt(b*b-4*a*c))/(2*a);
    r = {x1, x2};
    return r;
}

int main() {
    int a, b, c;
    cin >> a >> b >> c;
    int D = b*b-4*a*c;
    if (D > 0) {
        roots R = solve(a,b,c);
        cout << "Two different roots x1="
            << R.x1 << " , x2=" << R.x2 << '\n';
    }
    else if (D == 0)
        cout << "Two same roots x="
            << b/(-2*a) << '\n';
    else
        cout << "No real roots\n";
}

ZJ a042：平面圓形切割

假設平面上有n個圓

每多加一個圓，多產生2n個交點，

兩交點之間和周圍多圍出一塊，所以多產生2n塊

\(\Rightarrow a_{n+1}=a_n + 2n\)

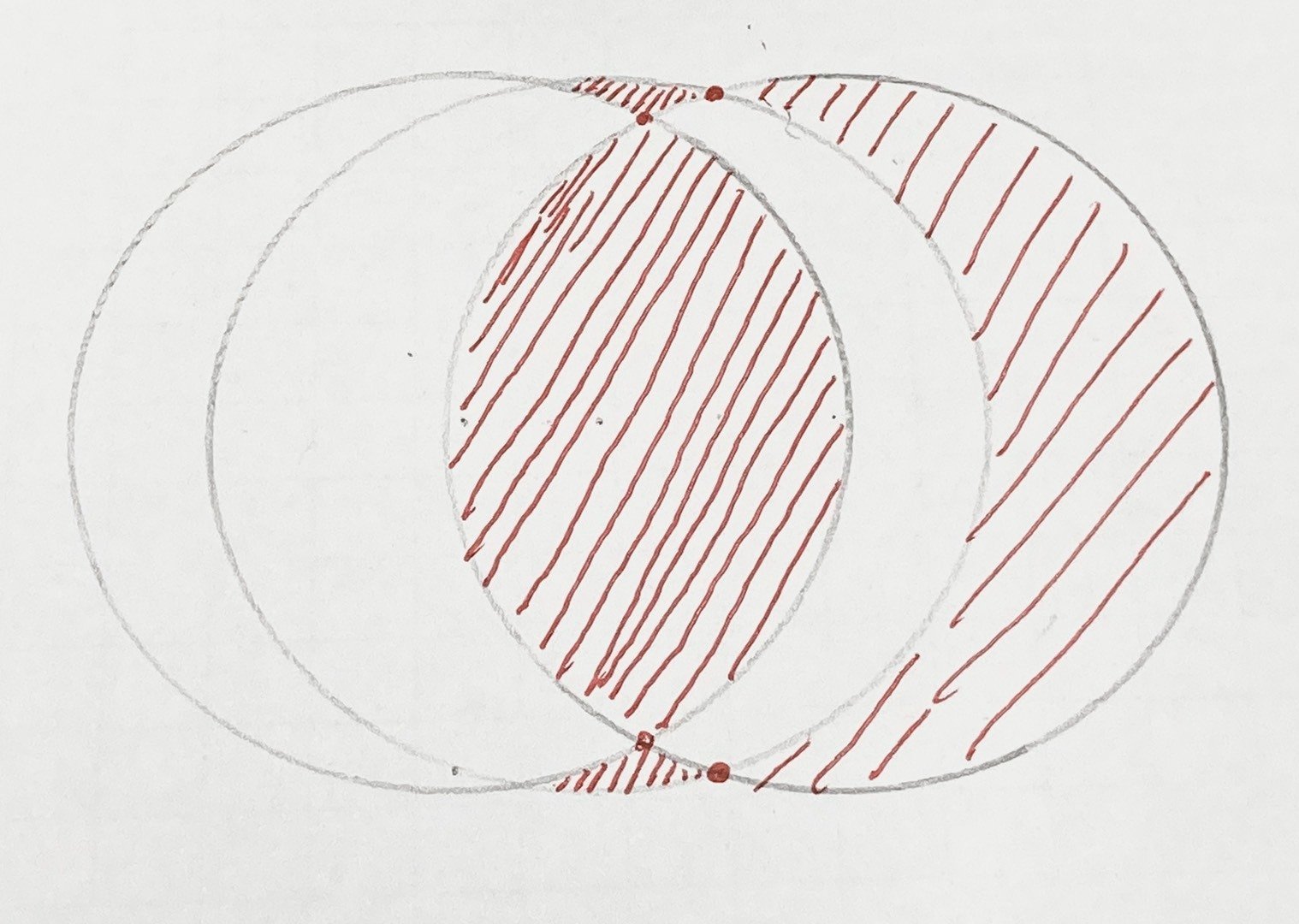
例：假設原本兩個圓，

最右邊多加一個圓，

截出\(2\times 2=4\)交點

比原本多產生4塊

#include <iostream>
using namespace std;

int f(int n) {
    if (n == 1) return 2;
    return f(n-1)+2*(n-1);
}

int main() {
    int x;
    while (cin >> x)
	cout << f(x) << '\n';
}

ZJ a042：平面圓形切割

\(a_n=\begin{cases}2,\ n=1\\a_{n-1} + 2(n-1),\ n\geq 2\end{cases}\)

把問題想成在n個格子塗色，遵守以下規則

左右兩端留白不超過1格
中間不允許超過2格相鄰的格子留白
任相鄰2格不可都塗色

ZJ d389：11069 - A Graph Problem

\(\dots \dots\)

討論塗\(n\)格（左到右）時的塗法（\(n>3\)）：

第\(n\)格有塗色，令有\(a_n\)種
第\(n\)格留白，第\(n-1\)格有塗，令有\(b_n\)種
第\(n\)格和第\(n-1\)格都留白，第\(n-2\)格有塗，令有\(c_n\)種

注意！第3種不是合法的塗法，但是第3種拿掉最右的白格後是合法的。合法的塗法一共\(a_n+b_n\)種。記錄第3種的原因是第3種右邊再塗一黑格就是合法的

ZJ d389：11069 - A Graph Problem

合法的塗法：

\(a_n+b_n\)種

\(a_n\)

\(b_n\)

\(c_n\)

\(\dots \dots\)

討論\(n+1\)格的塗法：用\(a_n, b_n, c_n\)推\(a_{n+1}, b_{n+1}, c_{n+1}\)

\(a_n\)後面加一格，第\(n\)格有塗色，所以第\(n+1\)格不能塗色，最右端會留白一格（也就是\(b_{n+1}\)）

\(\Rightarrow b_{n+1}=a_n\)

\(b_n, c_n\)後面加一格塗色，最右端塗色（也就是\(a_{n+1}\)）

\(\Rightarrow a_{n+1}=b_n+c_n\)

\(b_n\)後面加一個白格，最右端連空2格（也就是\(c_{n+1}\)）

\(\Rightarrow c_{n+1}=b_n\)

ZJ d389：11069 - A Graph Problem

\(\dots \dots\)

\(b_n\)加1格

\(c_n\)加1格

\(\begin{cases}a_3=1:\{1, 3\}\\b_3=1:\{2\}\\c_3=1:\{1\}\end{cases}\)

\(k = 1:\{1\}\) 1種
\(k = 2:\{1\}, \{2\}\) 2種
\(k = 3:\{1, 3\}, \{2\}\) 2種

討論\(n\leq 3\)時的合法子集：直接窮舉

\(\begin{cases}a_{n+1}=b_n+c_n\\b_{n+1}=a_n\\c_{n+1}=b_n\end{cases}\)

討論\(n>3\)時的合法子集：利用剛剛得到的遞迴式

\(\begin{cases}a_3=1:\{1, 3\}\\b_3=1:\{2\}\\c_3=1:\{1\}\end{cases}\)

（窮舉）

輸出\(a_n+b_n\)

ZJ d389：11069 - A Graph Problem

#include <iostream>
using namespace std;

int f(int n, int a=1, int b=1, int c=1) {
    if (n == 0) {
	return a+b; // 用n計算遞迴次數
    }
    return f(n-1, b+c, a, b);
}

int main() {
    int N;
    while (cin >> N) {
	if (N == 1)      cout << 1 << '\n';
	else if (N == 2) cout << 2 << '\n';
	else             cout << f(N-3) << '\n';
    }
}

合法子集有

\(a_n+b_n\)種

\(\begin{cases}a_{n+1}=b_n+c_n\\b_{n+1}=a_n\\c_{n+1}=b_n\end{cases}\)