Algorithms

Sort Algorithm

An algorithm is a set of instructions for solving a problem or accomplishing a task. One common example of an algorithm is a recipe, which consists of specific instructions for preparing a dish or meal.

Notations

The Big-O notation describes the worst-case running time of a program.

The Big-Θ (Theta) - represents the precise performance value of an algorithm or a practical range between tight upper and lower limits.

The Big-Ω (Omega) describes the best running time of a program.

Big O Complexity

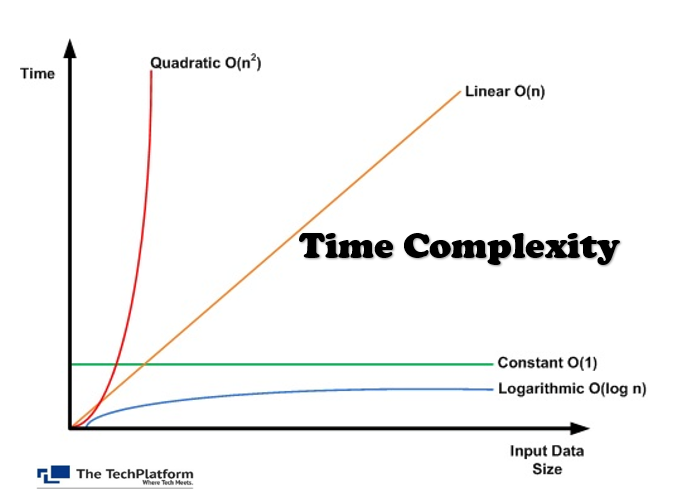
Constant: O(1)

Linear time: O(n)

Logarithmic time: O(n log n)

Quadratic time: O(n^2)

Exponential time: O(2^n)

Factorial time: O(n!)

Big O Complexity

O(1) - Excellent/Best

O(log n) - Good

O(n) - Fair

O(n log n) - Bad

O(n^2), O(2^n) and O(n!) - Horrible/Worst

Time complexity

Time complexity is defined as the amount of time taken by an algorithm to run, as a function of the length of the input

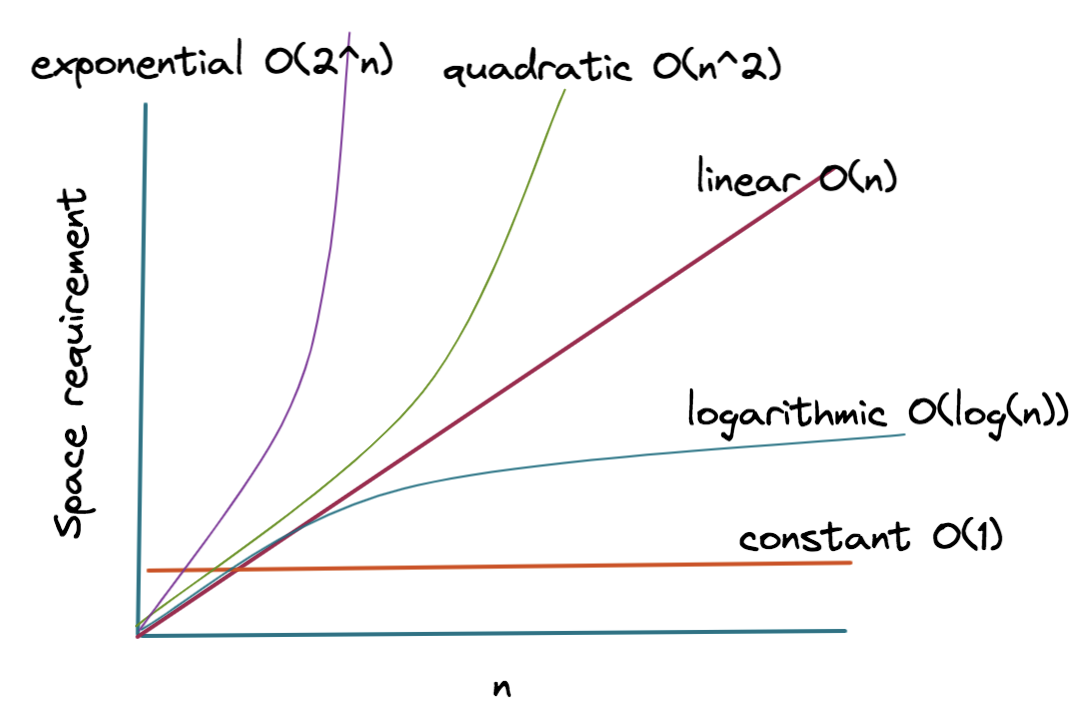
Space complexity

Space complexity refers to the total amount of memory space used by an algorithm/program, including the space of input values for execution

Big O of Objects

Insertion - O(1)

Removal - O(1)

Access - O(1)

Big O of Object Methods

Object.keys - O(N)

Object.values - O(N)

Object.entries - O(N)

hasOwnProperty - O(1)

Big O of Array Methods

push - O(1)

pop - O(1)

shift - O(N)

unshift - O(N)

concat - O(N)

slice - O(N)

splice - O(N)

sort - O(N * log N)

forEach/map/filter/reduce/etc. - O(N)

Sort Algorithms

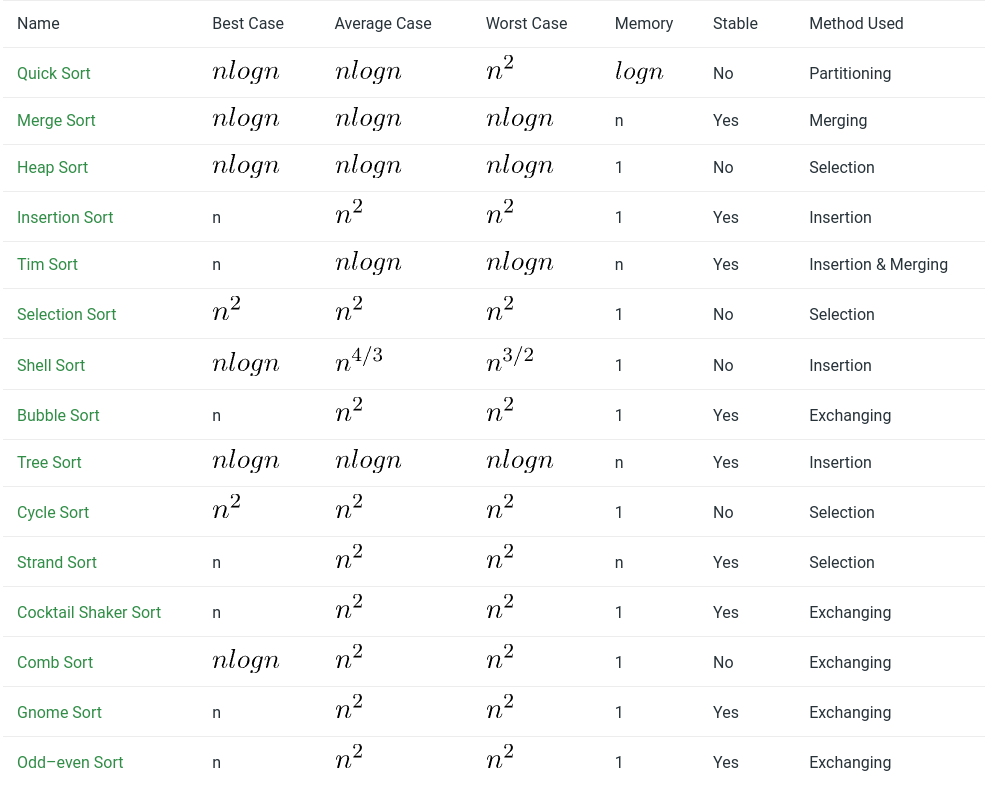
QuickSort

QuickSort is a sorting algorithm based on the Divide and Conquer algorithm that picks an element as a pivot and partitions the given array around the picked pivot by placing the pivot in its correct position in the sorted array.

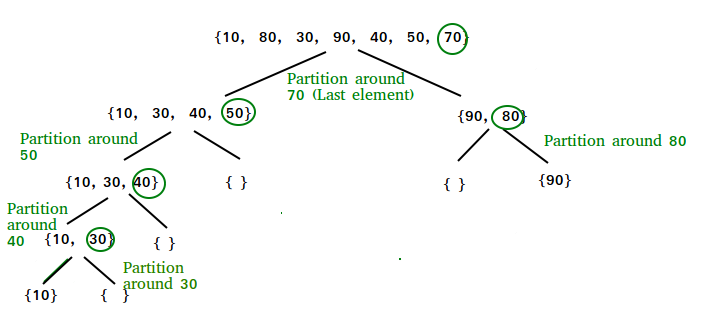
QuickSort

public static void QuickSort(int[] arr, int left, int right) {
    if (left < right) {
        int pivotIndex = Partition(arr, left, right);
        QuickSort(arr, left, pivotIndex - 1);
        QuickSort(arr, pivotIndex + 1, right);
    }
}

public static int Partition(int[] arr, int left, int right) {
    int pivotValue = arr[right];
    int pivotIndex = left;
    for (int i = left; i < right; i++) {
        if (arr[i] < pivotValue) {
            int temp = arr[i];
            arr[i] = arr[pivotIndex];
            arr[pivotIndex] = temp;
            pivotIndex++;
        }
    }
    int temp2 = arr[pivotIndex];
    arr[pivotIndex] = arr[right];
    arr[right] = temp2;
    return pivotIndex;
}

Bubble Sort

Bubble Sort is the simplest sorting algorithm that works by repeatedly swapping the adjacent elements if they are in the wrong order. This algorithm is not suitable for large data sets as its average and worst-case time complexity is quite high.

Bubble Sort

public static void BubbleSort(int[] arr) {
    int n = arr.Length;
    for (int i = 0; i < n - 1; i++) {
        for (int j = 0; j < n - i - 1; j++) {
            if (arr[j] > arr[j + 1]) {
                int temp = arr[j];
                arr[j] = arr[j + 1];
                arr[j + 1] = temp;
            }
        }
    }
}

// JS

function bubbleSort(arr) {
  let n = arr.length;
  for (let i = 0; i < n - 1; i++) {
    for (let j = 0; j < n - i - 1; j++) {
      if (arr[j] > arr[j + 1]) {
        let temp = arr[j];
        arr[j] = arr[j + 1];
        arr[j + 1] = temp;
      }
    }
  }
  return arr;
}

Insertion Sort

Insertion sort is a simple sorting algorithm that works similar to the way you sort playing cards in your hands. The array is virtually split into a sorted and an unsorted part. Values from the unsorted part are picked and placed at the correct position in the sorted part.

Insertion Sort

public static void InsertionSort(int[] arr)
{
    for (int i = 1; i < arr.Length; i++)
    {
        int key = arr[i];
        int j = i - 1;
        while (j >= 0 && arr[j] > key)
        {
            arr[j + 1] = arr[j];
            j--;
        }
        arr[j + 1] = key;
    }
}

// JS

function insertionSort(arr) {
  for (let i = 1; i < arr.length; i++) {
    let key = arr[i];
    let j = i - 1;
    while (j >= 0 && arr[j] > key) {
      arr[j + 1] = arr[j];
      j--;
    }
    arr[j + 1] = key;
  }
  return arr;
}

Merge Sort

Merge sort is defined as a sorting algorithm that works by dividing an array into smaller subarrays, sorting each subarray, and then merging the sorted subarrays back together to form the final sorted array.

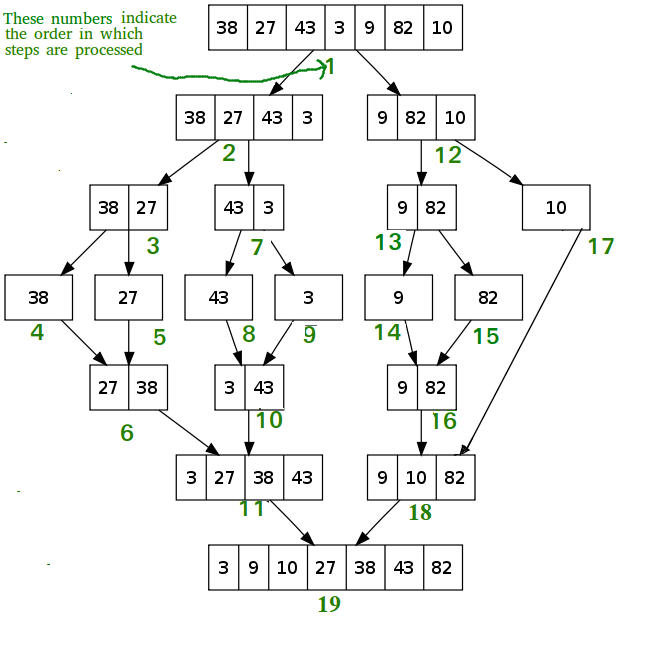
Merge Sort

public static void MergeSort(int[] arr, int left, int right) {
    if (left < right) {
        int mid = (left + right) / 2;
        MergeSort(arr, left, mid);
        MergeSort(arr, mid + 1, right);
        Merge(arr, left, mid, right);
    }
}

public static void Merge(int[] arr, int left, int mid, int right) {
    int[] temp = new int[right - left + 1];
    int i = left;
    int j = mid + 1;
    int k = 0;
    while (i <= mid && j <= right) {
        if (arr[i] < arr[j]) {
            temp[k] = arr[i];
            i++;
        } else {
            temp[k] = arr[j];
            j++;
        }
        k++;
    }
    while (i <= mid) {
        temp[k] = arr[i];
        i++;
        k++;
    }
    while (j <= right) {
        temp[k] = arr[j];
        j++;
        k++;
    }
    for (int p = 0; p < temp.Length; p++) {
        arr[left + p] = temp[p];
    }
}

Merge Sort

function mergeSort(arr) {
  if (arr.length <= 1) {
    return arr;
  }

  const middle = Math.floor(arr.length / 2);
  const left = arr.slice(0, middle);
  const right = arr.slice(middle);

  return merge(mergeSort(left), mergeSort(right));
}

function merge(left, right) {
  let result = [];
  let i = 0;
  let j = 0;

  while (i < left.length && j < right.length) {
    if (left[i].localeCompare(right[j]) < 0) {
      result.push(left[i]);
      i++;
    } else {
      result.push(right[j]);
      j++;
    }
  }

  return result.concat(left.slice(i)).concat(right.slice(j));
}

const arr = ["apple", "banana", "cherry", "date", "fig", "grape"];
const sortedArr = mergeSort(arr);

console.log(sortedArr);

Selection sort

Selection sort is a simple and efficient sorting algorithm that works by repeatedly selecting the smallest (or largest) element from the unsorted portion of the list and moving it to the sorted portion of the list.

Selection Sort

function selectionSort(arr) {
  for (let i = 0; i < arr.length - 1; i++) {
    let minIndex = i;
    for (let j = i + 1; j < arr.length; j++) {
      if (arr[j] < arr[minIndex]) {
        minIndex = j;
      }
    }
    if (minIndex !== i) {
      [arr[i], arr[minIndex]] = [arr[minIndex], arr[i]];
    }
  }
  return arr;
}

Selection Sort

public static void SelectionSort(int[] arr)
{
    for (int i = 0; i < arr.Length - 1; i++)
    {
        int minIndex = i;
        for (int j = i + 1; j < arr.Length; j++)
        {
            if (arr[j] < arr[minIndex])
            {
                minIndex = j;
            }
        }
        if (minIndex != i)
        {
            int temp = arr[i];
            arr[i] = arr[minIndex];
            arr[minIndex] = temp;
        }
    }
}

// Example usage:
int[] arr = { 5, 3, 8, 4, 2 };
SelectionSort(arr);
foreach (int num in arr)
{
    Console.Write(num + " "); // Output: 2 3 4 5 8
}