ビット演算・bit DP

aotsuki

今日やること

  • 基礎知識の確認
  • ビット演算
  • bitDP

基礎知識の確認

ビット

  • ビットとはコンピュータで扱われる情報量の最小単位のこと
  • "binary digit"を略したものが語源になっているといわれている
  • ビットは2進数で表現され、2進数の1桁 = 1ビット

バイト

  • バイトとはコンピュータで扱われる情報量の単位のこと
  • 1バイトは8ビットであらわす事ができる
  • 1バイトで最大256個の状態（数値）を表現することができる

2進数表記

  • 数値の先頭に0bをつけると2進数表記になる
  • 0xを付けると16進数、0を付けると8進数になる

例：142       2進数     0b10001110

        16進数　 0x8E

          8進数     0216

補数

  • 補数とはある値に加えると一定の基準値になる値のこと
  • 基準①：その桁数で最大の数
  • 基準②：桁が一つ繰り上がる数

基準 ①よって求められた値を2進数では『1の補数』

基準 ② よって求められた値を2進数では『2の補数』

という

補数

b進法において、自然数aを表現するのに必要な最小の桁数をnとしたとき、

  • b^n - a を、b進法におけるaに対する基数の補数　（bの補数）
  • b^n - a - 1 を、b進法におけるaに対する減基数の補数（b-1の補数）

という

(詳しく書くと...)

補数

１の補数

「足しても桁上がりしない数のうち最大の数」

　　(ここでいう桁とは演算範囲の桁数を指す )

 

補数

１の補数

「足しても桁上がりしない数のうち最大の数」

　　(ここでいう桁とは演算範囲の桁数を指す )

 

　例：0b01110100 → 　0b10001011

　　(0b01110100 + 0b 10001011 = 0b11111111)

 

補数

１の補数

「足しても桁上がりしない数のうち最大の数」

　　(ここでいう桁とは演算範囲の桁数を指す )

 

　例：0b01110100 → 　0b10001011

　　(0b01110100 + 0b 10001011 = 0b11111111)

 

　＝＞各ビットを反転させたもの

補数

２の補数

「桁が一つ繰り上がる数 」

　　 (ここでいう桁とは演算範囲の桁数を指す )

 

補数

２の補数

「桁が一つ繰り上がる数 」

　　 (ここでいう桁とは演算範囲の桁数を指す )

 

　例：0b01110100 → 　0b10001100

　　(0b01110100 + 0b 10001100 = 0b100000000)

 

補数

２の補数

「桁が一つ繰り上がる数 」

　　 (ここでいう桁とは演算範囲の桁数を指す )

 

　例：0b01110100 → 　0b10001100

　　(0b01110100 + 0b 10001100 = 0b100000000)

 

　＝＞各ビットを反転させ、1を足したもの

 

２進数による負の値の表現

コンピュータで2進数の負の値を表すときは絶対値の「２の補数」を使用して表現する

２進数による負の値の表現

コンピュータで2進数の負の値を表すときは絶対値の「２の補数」を使用して表現する

例：　-14

２進数による負の値の表現

コンピュータで2進数の負の値を表すときは絶対値の「２の補数」を使用して表現する

例：　-14

　　  |-14|=14 (0b00001110)の2の補数 

 

２進数による負の値の表現

コンピュータで2進数の負の値を表すときは絶対値の「２の補数」を使用して表現する

例：　-14

　　  |-14|=14 (0b00001110)の2の補数 

　　   →ビット反転  + 1   (0b11110001 + 1)

２進数による負の値の表現

コンピュータで2進数の負の値を表すときは絶対値の「２の補数」を使用して表現する

例：　-14

　　  |-14|=14 (0b00001110)の2の補数 

　　   →ビット反転  + 1   (0b11110001 + 1)

　　   →0b11110010

 

２進数による負の値の表現

コンピュータで2進数の負の値を表すときは絶対値の「２の補数」を使用して表現する

例：　-14

　　  |-14|=14 (0b00001110)の2の補数 

　　   →ビット反転  + 1   (0b11110001 + 1)

　　   →0b11110010

 

　　  14 + (-14) = 

２進数による負の値の表現

コンピュータで2進数の負の値を表すときは絶対値の「２の補数」を使用して表現する

例：　-14

　　  |-14|=14 (0b00001110)の2の補数 

　　   →ビット反転  + 1   (0b11110001 + 1)

　　   →0b11110010

 

　　  14 + (-14) = 0b00001110

                 　　  + 0b11110010

２進数による負の値の表現

コンピュータで2進数の負の値を表すときは絶対値の「２の補数」を使用して表現する

例：　-14

　　  |-14|=14 (0b00001110)の2の補数 

　　   →ビット反転  + 1   (0b11110001 + 1)

　　   →0b11110010

 

　　  14 + (-14) = 0b00001110

                 　　  + 0b11110010

                  　　  = 0b100000000

２進数による負の値の表現

コンピュータで2進数の負の値を表すときは絶対値の「２の補数」を使用して表現する

例：　-14

　　  |-14|=14 (0b00001110)の2の補数 

　　   →ビット反転  + 1   (0b11110001 + 1)

　　   →0b11110010

 

　　  14 + (-14) = 0b00001110

                 　　  + 0b11110010

                  　　  = 0b100000000

                 　　 → 0   ( 演算範囲は8桁だからあふれた9桁目は無視)

ビット演算

ビット演算とは

  • 各のビット全てに対する論理演算をいっぺんに行う演算操作

 

  • いろんなところで使える
  • Binary Indexed Tree (BIT)
  • bit 全探索
  • bit DP
  • ...

ビット演算の利点

  • データ量が少なくて済む
  • 多少速い
  • 一つのデータに複数の情報を詰め込める(フラグ管理など)

ビット演算子の種類

  • NOT  (否定)                            ~x 
  • AND  (論理積)                    x & y
  • OR  (論理和)                        x | y
  • XOR  (排他的論理和)         x ^ y
  • 右シフト                              x >> n
  • 左シフト                              x << n

NOT  (否定)        ~x 

x 0 1 1 0 0 1 0 1
~x 1 0 0 1 1 0 1 0
  • 1の補数
  • ビットを反転させる（0→1/1 →0）

AND  (論理積)    x&y 

x 1 0 0 1 1 1 0 0
y 1 1 0 0 1 0 1 0
x&y 1 0 0 0 1 0 0 0
  • 両方のビットが1の時、結果が1になる

OR  (論理和)    x|y 

  • どちらかのビットが1の時、結果が1になる
x 1 0 0 1 1 1 0 0
y 1 1 0 0 1 0 1 0
x|y 1 1 0 1 1 1 1 0

XOR  (排他的論理和)    x ^ y

  • 互いのビットが不一致の時、結果が1になる
x 1 0 0 1 1 1 0 0
y 1 1 0 0 1 0 1 0
x^y 0 1 0 1 0 1 1 0

右シフト    x >> n

  • 各ビットを右にn個ずらす
  • 　　　と 同じ
x 1 0 0 1 1 1 0 0
x>>n 0 0 1 0 0 1 1 1

{

{

n=2 

x : unsigned char

空いた桁は0で埋まる

このbitは捨てられる

x/{2^n}

(ほぼ)

左シフト    x << n

x 1 0 0 1 1 1 0 0
x<<n 0 1 1 1 0 0 0 0

{

{

n=2 

x : unsigned char

空いた桁は0で埋まる

このbitは捨てられる

  • 各ビットを左にn個ずらす
  • 桁があふれなければ　　　と 同じ
{x}*{2^n}

※注意点

シフトには２種類ある

※注意点

シフトには２種類ある

・算術シフト

シフトによって空いたビット部分を符号ビットを同じもので詰める

・論理シフト

シフトによって空いたビット部分を常に０で詰める

※注意点

シフトには２種類ある

・算術シフト

シフトによって空いたビット部分を符号ビットを同じもので詰める

・論理シフト

シフトによって空いたビット部分を常に０で詰める

符号が正のときはどちらも同じ

※注意点

シフトには２種類ある

・算術シフト

シフトによって空いたビット部分を符号ビットを同じもので詰める

・論理シフト

シフトによって空いたビット部分を常に０で詰める

符号が正のときはどちらも同じ

＝＞問題は符号が負のとき

※注意点

・論理シフト

x 1 0 0 1 1 1 0 0
x>>n 0 0 1 0 0 1 1 1

n=2 

x : unsigned char

空いた桁は０で埋まる

{

x 1 0 0 1 1 1 0 0
x<<n 0 1 1 1 0 0 0 0

※注意点

・算術シフト

x 1 0 0 1 1 1 0 0
x>>n 1 0 0 1 1 1

n=2 

x : signed char

空いた桁は　 で埋まる

{

x 1 0 0 1 1 1 0 0
x<<n 1 1 1 0 0 0 0

１

１

１

１

=>常に符号は変わらない

※注意点

これらはコンパイラによって決まる

gccでは

算術シフト　 signed int/long/long long

論理シフト　un signed int/long/long long

予期せぬ挙動をすることがあるので注意！

bit に i 番目のフラグが立っているか
(0-indexed) 		if (bit & (1<<i))
bit に i 番目のフラグが消えているか if (!(bit & (1<<i)))
bit に i 番目のフラグを立てる bit｜= (1<<i)
bit に i 番目のフラグを消す bit &= ~(1<<i)
bit に何個のフラグが立っているか __builtin_popcount(bit)　(int)
__builtin_popcountl(bit)　(long)
__builtin_popcountll(bit)　(long long)
小さい方から何桁目に初めて立ったフラグが現れるか
(1-indexed) 		__builtin_ffs(bit)　(int)
__builtin_ffsl(bit)　(long)
__builtin_ffsll(bit)　(long long)

フラグ管理

std::bitset を用いた出力

#include <iostream>
#include <bitset>
using namespace std;

int main() {
    int A = 0x2d;
    int B = 0x19;
    cout << bitset<8>(A) << " AND " << bitset<8>(B) << " = " << bitset<8>(A&B) << endl;
}
00101101 AND 00011001 = 00001001

出力

std::bitsetを使うと2進数で出力できる

bit DP

bit DPとは

n個の要素の順列 (n!通り) としてありうるものの中から、最適なものを求めたい場面でしばしば使えるテクニック

巡回セールスマン問題

街がN+1個あります。

街0から全ての街を通って帰ってきたいです。

最短となる経路の長さを求めなさい。

ただし、N≤15。

※ NP困難問題と呼ばれる部類らしい

巡回セールスマン問題

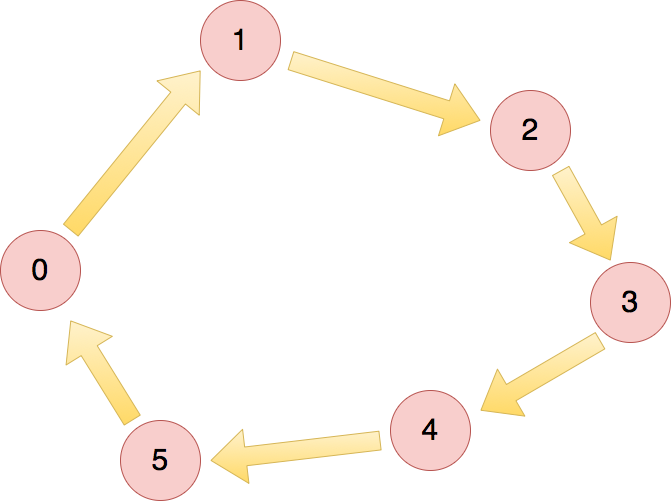
例えば、N=5の時...

巡回セールスマン問題

例えば、N=5の時...

巡回セールスマン問題

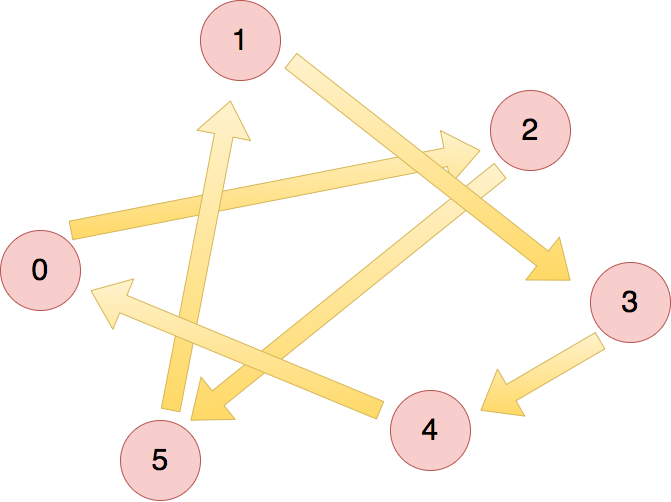
例えば、N=5の時...

巡回セールスマン問題

愚直にやると...

　N個の順列　=> 　O(N !)

 

巡回セールスマン問題

愚直にやると...

　N個の順列　=> 　O(N !)

 

N=8...　　  N ! ≤ 

10^5

巡回セールスマン問題

愚直にやると...

　N個の順列　=> 　O(N !)

 

N=8...　　  N ! ≤ 

10^5

N=10...　　N ! ≤ 

10^8

巡回セールスマン問題

愚直にやると...

　N個の順列　=> 　O(N !)

 

N=8...　　  N ! ≤ 

10^5

N=10...　　N ! ≤ 

10^8

N=15...　　N ! ≤ 

10^{13}

巡回セールスマン問題

愚直にやると...

　N個の順列　=> 　O(N !)

 

N=8...　　  N ! ≤ 

10^5

N=10...　　N ! ≤ 

10^8

N=15...　　N ! ≤ 

10^{13}

<= 間に合わない

巡回セールスマン問題

そこで...

巡回セールスマン問題

そこで...　

bitDP！

巡回セールスマン問題

そもそも、

DP(動的計画法)とは何だったか？

巡回セールスマン問題

そもそも、

DP(動的計画法)とは何だったか？

 

　=>それまでの状態をまとめる！

巡回セールスマン問題

そもそも、

DP(動的計画法)とは何だったか？

 

　=>それまでの状態をまとめる！

 

　=>今回の場合は？

巡回セールスマン問題

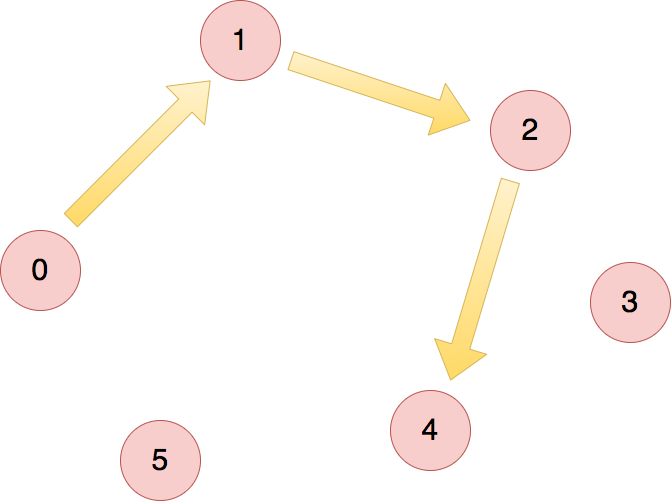
例えば、ここまで調べた場合...

巡回セールスマン問題

例えば、ここまで調べた場合...

「ここから先が完全に一緒で、ここまでの経路が違うもの」をまとめたい！

巡回セールスマン問題

0→1 →2→4  とこの先が同じになるのはどんな時？​

巡回セールスマン問題

0→1 →2→4  とこの先が同じになるのはどんな時？​

・0→2 →1→4  など。(4から出発して{3, 5}をめぐり0に戻る)

巡回セールスマン問題

0→1 →2→4  とこの先が同じになるのはどんな時？​

共通しているものは？

  • ここまでに通ってきた街の集合
  • 最後に訪れた街

・0→2 →1→4  など。(4から出発して{3, 5}をめぐり0に戻る)

巡回セールスマン問題

0→1 →2→4  とこの先が同じになるのはどんな時？​

共通しているものは？

  • ここまでに通ってきた街の集合
  • 最後に訪れた街

＝＞これを使ってまとめればいい！

・0→2 →1→4  など。(4から出発して{3, 5}をめぐり0に戻る)

巡回セールスマン問題

「ここまでに通ってきた街の集合」ってどう持っておけばいいんだろう？

巡回セールスマン問題

「ここまでに通ってきた街の集合」ってどう持っておけばいいんだろう？

＝＞　ビットで表せばいい！

巡回セールスマン問題

i番目の街に訪れた　　　＝＞　i桁目のビットを1

i番目の街に訪れてない　＝＞　i桁目のビットを0

　にする

巡回セールスマン問題

i番目の街に訪れた　　　＝＞　i桁目のビットを1

i番目の街に訪れてない　＝＞　i桁目のビットを0

　にする

そうすることで「ここまでに通ってきた街の集合」を保持することが可能に！

巡回セールスマン問題

あとは普通のDPと同じ！

 

　　(配るDPの方が楽そう...)

巡回セールスマン問題

計算量

  • 最後に訪れた街の種類が最大 N通り
  • 街の状態数は　　通り
  • 各状態に対して 次の街の選択肢が最大 N通り
2^N

巡回セールスマン問題

計算量

  • 最後に訪れた街の種類が最大 N通り
  • 街の状態数は　　通り
  • 各状態に対して 次の街の選択肢が最大 N通り
O(2^N \times N^2)
2^N

よって全体の計算量は

N=15  でも間に合う

参考文献

https://qiita.com/drken/items/7c6ff2aa4d8fce1c9361#bit-dp

https://www.slideshare.net/chokudai/wap-atcoder4

http://naoyat.hatenablog.jp/entry/2014/05/12/143650

https://yttm-work.jp/pgtheory/pgtheory_0019.html

https://qiita.com/satellitesat/items/340de8a946ddd2bac24e

Made with Slides.com