競技プログラミング練習会
2019 Normal
第5回 動的計画法
担当：laft
slides.com/procon2019/deck-7/fullscreen
自己紹介
自己紹介
- 京都大学工学部情報学科2回生
- 本名：平井 雅人
- CとC++を普段使ってます。
- よろしくお願いします。
KMC-ID:laft
皆さんの自己紹介もお願いします
- 名前(部員の方はKMC-ID)
- 所属(大学など？)
- 使える言語や使う予定の言語
- プログラミング経験や競プロの経験(もちろんなくても大丈夫です！)
- 趣味・特技・意気込みなど
あくまで一例ですが、下を参考に
新しく来た人だけで良さそう
今日の内容
今日の内容
- メモ化再帰
- 動的計画法(DP)とは
- もらうDP
- 配るDP
動的計画法
動的計画法とは
- 愚直に全探索や、定義通りに計算して間に合わなくても、途中の計算結果(部分的な解)を用いることで、高速化できることがある。
- このような手法で高速化する方法を動的計画法(DP,Dynamic Programming)という。
例題：フィボナッチ数列
- フィボナッチ数列:
- この数列の第n項を求めよ。
- 制約：
F_0=1,F_1=1,F_{n}=F_{n-1}+F_{n-2}\ (n\geqq2)
\{ F_n\} = \{ 0,1,1,2,3,5,8,13,21,34,..\}
1\leqq n \leqq 90
実行時間制限：2sec
解法１：愚直解
- 定義通りの関数を作成して実行すれば完成。
#include<bits/stdc++.h>
using namespace std;
long long fib(int n){
if(n==0) return 0;
if(n==1) return 1;
return fib(n-1) + fib(n-2);
}
int main(){
int n;
cin >> n;
cout << fib(n) << endl;
}解法１：愚直解の計算量
- このコードだと、すごいたくさん再帰呼び出しが発生する。
fib(10) = fib(9) + fib(8)解法１：愚直解の計算量
- このコードだと、すごいたくさん再帰呼び出しが発生する。
fib(10) = fib(9) + fib(8)
= (fib(8)+fib(7)) + (fib(7)+fib(6))解法１：愚直解の計算量
- このコードだと、すごいたくさん再帰呼び出しが発生する。
fib(10) = fib(9) + fib(8)
= (fib(8)+fib(7)) + (fib(7)+fib(6))
= ((fib(7)+fib(6))+(fib(6)+fib(5))
+ ((fib(6)+fib(5))+(fib(5)+fib(4))解法１：愚直解の計算量
- このコードだと、すごいたくさん再帰呼び出しが発生する。
fib(10) = fib(9) + fib(8)
= (fib(8)+fib(7)) + (fib(7)+fib(6))
= ((fib(7)+fib(6))+(fib(6)+fib(5))
+ ((fib(6)+fib(5))+(fib(5)+fib(4))
= (((fib(6)+fib(5))+(fib(5)+fib(4)))
+ ((fib(5)+fib(4))+(fib(4)+fib(3))))
+ (((fib(5)+fib(4))+(fib(4)+fib(3)))
+ ((fib(4)+fib(3))+(fib(3)+fib(2))))解法１：愚直解の計算量
- このコードだと、すごいたくさん再帰呼び出しが発生する。
fib(10) = fib(9) + fib(8)
= (fib(8)+fib(7)) + (fib(7)+fib(6))
= ((fib(7)+fib(6))+(fib(6)+fib(5))
+ ((fib(6)+fib(5))+(fib(5)+fib(4))
= (((fib(6)+fib(5))+(fib(5)+fib(4)))
+ ((fib(5)+fib(4))+(fib(4)+fib(3))))
+ (((fib(5)+fib(4))+(fib(4)+fib(3)))
+ ((fib(4)+fib(3))+(fib(3)+fib(2))))
= 以下同様に……解法１：愚直解の計算量
- 1つの関数が概ね2つの再帰呼び出しをしているのでおそらく指数オーダー
- 実際、 になる。
- さっきのn=10の例でも再帰呼び出しの数は176回(laft調べ)
- これは、n=40程度で実行時間制限に間に合わなくなることが知られている。
- 僕の手元でn=41までが2secに収まった。
O((\frac{1+\sqrt5}{2})^n)
解法１の考察
fib(10) = fib(9) + fib(8)
= (fib(8)+fib(7)) + (fib(7)+fib(6))
= ((fib(7)+fib(6))+(fib(6)+fib(5))
+ ((fib(6)+fib(5))+(fib(5)+fib(4))
= (((fib(6)+fib(5))+(fib(5)+fib(4)))
+ ((fib(5)+fib(4))+(fib(4)+fib(3))))
+ (((fib(5)+fib(4))+(fib(4)+fib(3)))
+ ((fib(4)+fib(3))+(fib(3)+fib(2))))
= 以下同様に……
解法１の考察
fib(10) = fib(9) + fib(8)
= (fib(8)+fib(7)) + (fib(7)+fib(6))
= ((fib(7)+fib(6))+(fib(6)+fib(5))
+ ((fib(6)+fib(5))+(fib(5)+fib(4))
= (((fib(6)+fib(5))+(fib(5)+fib(4)))
+ ((fib(5)+fib(4))+(fib(4)+fib(3))))
+ (((fib(5)+fib(4))+(fib(4)+fib(3)))
+ ((fib(4)+fib(3))+(fib(3)+fib(2))))
= 以下同様に……
fib(6)は5回も呼び出されてる。
これは明らかに無駄！
解法１の考察
- 同じnに対してfib(n)の返す値は同じなのに、それら全てが個々に再帰しているのが無駄。
- じゃあ一回計算したら、その値をメモって再利用すれば良くね？→メモ化再帰
- そもそもnの小さい方から漸化式で一意に決めてそこから計算すれば良くね？→もらうDP
-
一般項って知ってる？→...(今日はやりません)- 愚直にやると浮動小数誤差で実用的ではない
メモ化再帰
解法２：メモ化再帰
- dpという配列を用意しておく。
- fib(i)を１回計算した時にdp[i]に値を保存する。
- dp[i]に計算済みの値が入っていれば再帰せずにそれを返す。
- こうすると、各fib(i)を1度しか計算しないので大きな節約になる。
- このように、計算済みの値で再帰数を大幅に減らすDPをメモ化再帰という。
解法２：メモ化再帰のコード例
#include<bits/stdc++.h>
using namespace std;
//mainなどの関数に入れずに作った変数をグローバル変数という。
//グローバル変数はどの関数からでも参照できる。
vector<long long> dp;
long long fib(int n){
if(dp[n]!=-1) return dp[n];
if(n==0) return 0;
if(n==1) return 1;
return dp[n] = fib(n-1) + fib(n-2);
}
int main(){
int n;
cin >> n;
//assignはvectorのサイズと中身を同時に設定する関数。
//これは初期化と全く同様に使える。[0,n]に-1をセット。
dp.assign(n+1,-1);
cout << fib(n) << endl;
}解法２の計算量考察
これが解法１の時の再帰
ついでに探索順序の確認もしよう。
解法２の計算量考察
これが解法１の時の再帰
ついでに探索順序の確認もしよう。
解法２の計算量考察
これが解法１の時の再帰
ついでに探索順序の確認もしよう。
解法２の計算量考察
これが解法１の時の再帰
ついでに探索順序の確認もしよう。
解法２の計算量考察
これが解法１の時の再帰
ついでに探索順序の確認もしよう。
解法２の計算量考察
これが解法１の時の再帰
ついでに探索順序の確認もしよう。
解法２の計算量考察
これが解法１の時の再帰
ついでに探索順序の確認もしよう。
ここでfib(2)の値が計算終了
解法２の計算量考察
これが解法１の時の再帰
ついでに探索順序の確認もしよう。
解法２の計算量考察
これが解法１の時の再帰
ついでに探索順序の確認もしよう。
解法２の計算量考察
これが解法１の時の再帰
ついでに探索順序の確認もしよう。
解法２の計算量考察
これが解法１の時の再帰
ついでに探索順序の確認もしよう。
解法２の計算量考察
これが解法１の時の再帰
ついでに探索順序の確認もしよう。
解法２の計算量考察
これが解法１の時の再帰
ついでに探索順序の確認もしよう。
解法２の計算量考察
これが解法１の時の再帰
ついでに探索順序の確認もしよう。
解法２の計算量考察
これが解法１の時の再帰
ついでに探索順序の確認もしよう。
解法２の計算量考察
こんな感じ！
再帰してるので深さ優先になります。
次に解法２のイメージ
解法２の計算量考察
次に解法２のイメージ
解法２の計算量考察
次に解法２のイメージ
解法２の計算量考察
次に解法２のイメージ
解法２の計算量考察
次に解法２のイメージ
解法２の計算量考察
次に解法２のイメージ
解法２の計算量考察
ここでfib(2)の値をdp[2]に格納しておく
次に解法２のイメージ
解法２の計算量考察
dp[3]に格納
次に解法２のイメージ
解法２の計算量考察
dp[2]の値を使えばいいので下に行かなくて良い
次に解法２のイメージ
解法２の計算量考察
dp[2]の値を使えばいいので下に行かなくて良い
dp[4]に格納
次に解法２のイメージ
解法２の計算量考察
dp[3]を使う
次に解法２のイメージ
こんな風に、再帰回数を大幅に減らせる。
解法２の計算量考察
dp[3]を使う
解法２の計算量の考察
- 今回の場合は関数呼び出しの回数を15回から9回まで減らせた。
- さっきの図に付け足す形でfib(6)を求めるのをイメージしてみよう。
解法２の計算量の考察
- さっきの図に付け足す形でfib(6)を求めるのをイメージしてみよう。
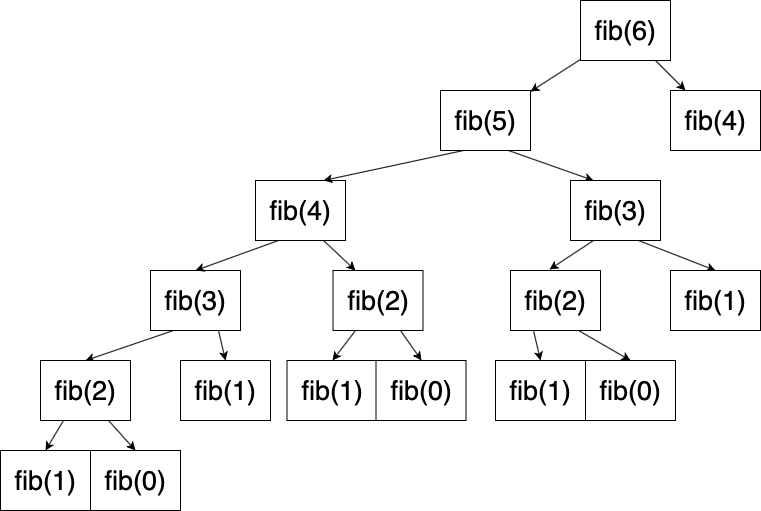
解法２の計算量の考察
- さっきの図に付け足す形でfib(6)を求めるのをイメージしてみよう。
fib(4)は既に求めているので再帰しなくていい。
解法２の計算量の考察
- さっきの図に付け足す形でfib(6)を求めるのをイメージしてみよう。
fib(4)は既に求めているので再帰しなくていい。
fib(6)で増えた呼び出しは2つだけ
解法２の計算量の考察
- さっきの図に付け足す形でfib(6)を求めるのをイメージしてみよう。
fib(4)は既に求めているので再帰しなくていい。
fib(6)で増えた呼び出しは2つだけ
fib(7)が増えても増える呼び出しは2つだけ
解法２の計算量の考察
- 今回の場合は関数呼び出しの回数を15回から9回まで減らせた。
- さっきの図に付け足す形でfib(6)を求めるのをイメージしてみよう。
- nが1増えても増える呼び出しは2つだけ。
- O(N)で求められる！！
もらうDP
もらうDPとは
- N=0(or1)で解けて、その解を使って、より大きいNについて順番に決めていくDP。
- 要は漸化式で過去の値から今見てる値を決めていくイメージ。
解法３：もらうDP
- サイズn+1の配列dpを作っておく。
- dp[0]=0, dp[1]=1としておく。
- dp[n]=dp[n-1]+dp[n-2]としてn=2から順番に計算する。
- 一番ぱっと思いつく方法な気はする。
解法３：もらうDPのコード例
#include<bits/stdc++.h>
using namespace std;
int main(){
int n;
cin >> n;
//[0,n]の配列dpを作る。
//dp[i]はフィボナッチ数列のi番目
vector<long long> dp(n+1);
dp[0] = 0;
dp[1] = 1;
for(int i=2;i<=n;++i){
dp[i] = dp[i-1] + dp[i-2];
}
cout << dp[n] << endl;
}解法３の考察
- O(N)
- この程度の問題なら、DPとか知らなくても、最初にこの解法を思いつく人もいるんでは
配るDP
配るDPとは
- 確定した値から、未確定の値に渡しておくことで、手前から順番に確定させていくDP。
- 漸化式によって、今見てる値から影響を与える先の値に渡していく。
解法４：配るDP
- サイズn+1,初期値0の配列dpを作っておく。
- dp[0]=0, dp[1]=1としておく。
- n=0から、dp[n+1]+=dp[n], dp[n+2]+=dp[n]としてnを増やしながら計算すると、次の値に足し合わせる時にはdp[n]は確定している。
解法４：配るDPのコード例
#include<bits/stdc++.h>
using namespace std;
int main(){
int n;
cin >> n;
//[0,n]の配列dpを作る。
//dp[i]はフィボナッチ数列のi番目
vector<long long> dp(n+1,0);
dp[0] = 0;
dp[1] = 1;
for(int i=0;i<n;++i){
dp[i+1] += dp[i];
if(i+2<=n) dp[i+2] += dp[i];
}
cout << dp[n] << endl;
}解法４：配るDPのコード例
#include<bits/stdc++.h>
using namespace std;
int main(){
int n;
cin >> n;
//[0,n]の配列dpを作る。
//dp[i]はフィボナッチ数列のi番目
vector<long long> dp(n+2,0); //こうすると後のif文を無くせる
dp[0] = 0;
dp[1] = 1;
for(int i=0;i<n;++i){
dp[i+1] += dp[i];
dp[i+2] += dp[i]; //if文消滅！！！！
}
cout << dp[n] << endl;
}解法４：配るDPのコード例の説明
| n | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| dp[n] | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
今の値を1つ次,2つ次の値に追加する。
解法４：配るDPのコード例の説明
| n | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| dp[n] | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
今の値を1つ次,2つ次の値に追加する。
解法４：配るDPのコード例の説明
| n | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| dp[n] | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
今の値を1つ次,2つ次の値に追加する。
解法４：配るDPのコード例の説明
| n | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| dp[n] | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
今の値を1つ次,2つ次の値に追加する。
解法４：配るDPのコード例の説明
| n | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| dp[n] | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 |
今の値を1つ次,2つ次の値に追加する。
解法４：配るDPのコード例の説明
| n | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| dp[n] | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 |
今の値を1つ次,2つ次の値に追加する。
解法４：配るDPのコード例の説明
| n | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| dp[n] | 0 | 1 | 1 | 2 | 1 | 0 | 0 | 0 | 0 |
今の値を1つ次,2つ次の値に追加する。
解法４：配るDPのコード例の説明
| n | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| dp[n] | 0 | 1 | 1 | 2 | 3 | 2 | 0 | 0 | 0 |
今の値を1つ次,2つ次の値に追加する。
解法４：配るDPのコード例の説明
| n | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| dp[n] | 0 | 1 | 1 | 2 | 3 | 5 | 3 | 0 | 0 |
今の値を1つ次,2つ次の値に追加する。
解法４：配るDPのコード例の説明
| n | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| dp[n] | 0 | 1 | 1 | 2 | 3 | 5 | 8 | 5 | 0 |
今の値を1つ次,2つ次の値に追加する。
解法４：配るDPのコード例の説明
| n | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| dp[n] | 0 | 1 | 1 | 2 | 3 | 5 | 8 | 13 | 8 |
今の値を1つ次,2つ次の値に追加する。
解法４：配るDPのコード例の説明
| n | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| dp[n] | 0 | 1 | 1 | 2 | 3 | 5 | 8 | 13 | 21 |
今の値を1つ次,2つ次の値に追加する。
解法４：配るDPのコード例の説明
| n | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| dp[n] | 0 | 1 | 1 | 2 | 3 | 5 | 8 | 13 | 21 |
今の値を1つ次,2つ次の値に追加する。
解法４の考察
- O(N)
- 今回の問題では明らかに解法３の方がわかりやすい。
- なので普通はこうは書かないと思う…
- このように、もらうDPの方が書きやすい問題と配るDPの方が書きやすい問題があるので、使い分けていこう。
例題２：ナップサック問題
愚直解とメモ化再帰
例題２：ナップサック問題
- \(n\)個の品物がある。
- \(i\)番目の品物は重さ\(w_i\),価値\(v_i\)
- ナップサックには合計重さWまで入れられる。
- ナップサックに入れるものの価値を最大化せよ
制約
1\leqq n\leqq 10^3 \\
1\leqq w_i \leqq 10^3 \\
1\leqq v_i \leqq 10^6 \\
1\leqq W \leqq 10^3 \\
例題２：ナップサック問題
n=4, W=7
w_i
v_i
具体例
| 1 | 2 | 3 | 4 | |
| 3 | 2 | 1 | 3 | |
| 5 | 3 | 4 | 4 |
i
この時、i=1,3,4を選ぶと価値の合計は13となり、最大となる。
解法１：全探索
全てについて取るか取らないか試してみる?
- 品物1を取る
- 品物2を取る。
- 品物3を取る。
- 品物3を取らない。
- 品物2を取らない。
- 品物3を取る。
- 品物3を取らない。
- 品物2を取る。
- 品物1を取らない。
- ……
解法１：全探索のコード
全てについて取るか取らないか試してみる?
int n,W;//main関数で入力しておく。
vector<int> w,v; //同上
//i番目の品物を選ぶ場合と選ばない場合の両方を試す。
//cwは選んだ物の重さの合計
int solve(int i,int cw){ //solve(0,W)で解を返す関数
//深さがnになるまで探索したら終了する。
if(i==n) return 0; //もう品物がないので0を返す。
int take;
//取る場合の値を再帰によって得る。取れる時は
if(cw+w[i]<W) take = v[i] + solve(i+1,cw+w[i]);
//取れない時は影響のない-1を代入。
else take = -1;
//取らない場合の値を再帰によって得る。
int untake = solve(i+1,cw);
//双方の大きい方を返す。
return max(take,untake);
}解法１の考察
- 全てについて取るか否かを試している。
- だいたい\(O(2^N)\)くらい
- \(N\leqq 10^3\)なので間に合わない…
- というわけでメモ化してみよう
解法２：メモ化再帰
- さっきの関数solve()には、引数が\(i,cw\)の2つあった。
- これらについてメモ化してみる。
- 二次元配列dpについてメモ化しよう。
- dp[i][j]=solve(i,j)
- \(0\leqq i\leqq n,\ 0\leqq cw\leqq W\)なので、配列サイズは高々\(nW\)
解法２：メモ化再帰のコード
int n,W;//main関数で入力しておく。
vector<int> w,v; //同上
vector<vector<int>> dp;//予め、全て-1でサイズn*(W+1)で初期化
//i番目の品物を選ぶ場合と選ばない場合の両方を試す。
//cwは選んだ物の重さの合計
int solve(int i,int cw){//solve(0,W)で解を返す。
if(i==n) return 0;
if(dp[i][cw]!=-1) return dp[i][cw];
int take = -1;
//取る場合の値を再帰によって得る。
if(cw+w[i]<W) take = solve(i+1,cw+w[i]);
//取らない場合の値を再帰によって得る。
int untake = solve(i+1,cw);
//双方の大きい方を返す。
return dp[i][cw] = max(take,untake);
}
解法２：メモ化再帰の考察
- メモ化すると、一度計算されたら、そのメモが呼び出されるので計算しなくて良い。
- よって\(O(nW)\)になる。
- 結局のところ、関数の引数の範囲でメモを作っておいて、それを利用しながら再帰すれば良い。
解法２：メモ化再帰の注意
int n,W;//main関数で入力しておく。
vector<int> w,v; //同上
//i番目の品物を選ぶ場合と選ばない場合の両方を試す。
//cwは選んだ物の重さの合計,cvは選んだ物の価値の合計
int solve(int i,int cw,int cv){ //solve(0,W,0)で解を返す関数
//深さがnになるまで探索したら終了する。
if(i==n){
if(cw<W) return cv;
else return -1; //選んだ物が条件を満たさない時-1を返す。
}
int take = solve(i+1,cw+w[i],cv+v[i]);
int untake = solve(i+1,cw,cv);
return max(take,untake);
}こんな風に引数を3つの関数にしたり、引数のサイズを制限しない時、計算量的にメモ化再帰しても間に合わない。(そもそもしにくい)
メモ化再帰のまとめ
- 全探索ができるなら、メモ化再帰の実装は然程難しくない。
- 但し、引数のサイズが有限であることが必要。
- また、引数の数はできるだけ減らしておかないと計算量が落ちにくいので注意。
例題２：ナップサック問題
もらうDP
もらうDPをしよう
- もらうDPをするために、どのように問題を分割するか考える。
- まず、nについて分割するのはできそう。
- 次にWについて分割するのもできそう。
- そこで、\(V_{n,W}:=((n,W)の時の答え)\)とする。
- 要は、\(V_{i,j}\)はi番目(1-indexed)までの品物を選んで、合計の重さをj以下にした時の合計価値の最大値のこと。
もらうDPをしよう
- 問題を分割したら、その部分問題が解けたと仮定した時に、そこからnとWをより大きくした部分問題を解けないか考える。
- つまり、漸化式(遷移)を考えるということ。
n番目の品を取る時が最大になるとしたら
V_{n,W}=V_{n-1,W-w[n]}+v[n]
n番目の品を取らない時が最大になるとしたら
V_{n,W}=V_{n-1,W}
になりそう
なぜその遷移に？
n番目の品を取る時が最大になるとしたら
V_{n,W}=V_{n-1,W-w[n]}+v[n]
n番目の品を取らない時が最大になるとしたら
V_{n,W}=V_{n-1,W}
n番目の品を取る時は、それがそもそも無い時でかつ、その品の重さ分がそもそも無かった時の最大値にv[n]を足したものが答えになる。
n番目の品を取らない時は、それがそもそも無い時でかつ、今のWと同じ時の最大値が答えになる。
結局、遷移はどうなるの
V_{n,W}=\max\{ V_{n-1,W-w[n]}+v[n],V_{n-1,W}\}
- 逆に、これ以外で が最大になるケースは存在しないのは明らか。
- じゃあさっきの２つの最大値を取れば良さそう。
V_{n,W}
V_{n,W}=V_{n-1,W}
あっW-w[n]<0の時はもちろん
初項を決めよう
- 遷移を決めたので次は初項を決めよう。
- 初項は遷移の元なので大事。
- nかWのどっちかが0なら、\(V_{n,W}\)は0になる。（そもそも1つも選べないので）
- また、遷移の時に遷移元が確定している必要があるので確認。
- 内側でWについてループを回し、外でnについてループを回せば、遷移元がn-1であることから大丈夫そう。
解法３：もらうDP
- n,Wについてループを回す。
- たったそれだけ
V_{n,W}
= \begin{cases} \max\{ V_{n-1,W-w[n]}+v[n],V_{n-1,W}\}(W-w[n]\geqq 0)\\
V_{n-1,W}\hspace{111pt}(W-w[n]<0)
\end{cases}
遷移
解法３：もらうDP：図
V_{n,W}
= \begin{cases} \max\{ V_{n-1,W-w[n]}+v[n],V_{n-1,W}\}(W-w[n]\geqq 0)\\
V_{n-1,W}\hspace{111pt}(W-w[n]<0)
\end{cases}
| 3 | 5 |
| 2 | 3 |
| 1 | 4 |
| 3 | 4 |
w_i
v_i
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | |||||||
| 0 | |||||||
| 0 | |||||||
| 0 |
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
| 0 | ||||||||
| 1 | ||||||||
| 2 | ||||||||
| 3 | ||||||||
| 4 |
i
j
n
W
解法３：もらうDP：図
V_{n,W}
= \begin{cases} \max\{ V_{n-1,W-w[n]}+v[n],V_{n-1,W}\}(W-w[n]\geqq 0)\\
V_{n-1,W}\hspace{111pt}(W-w[n]<0)
\end{cases}
| 3 | 5 |
| 2 | 3 |
| 1 | 4 |
| 3 | 4 |
w_i
v_i
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | |||||||
| 0 | |||||||
| 0 | |||||||
| 0 |
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
| 0 | ||||||||
| 1 | ||||||||
| 2 | ||||||||
| 3 | ||||||||
| 4 |
i
j
n
W
取る時、\((i-1,j-w[i])\)から遷移
取らない時、\((i-1,j)\)から遷移
解法３：もらうDP：図
V_{n,W}
= \begin{cases} \max\{ V_{n-1,W-w[n]}+v[n],V_{n-1,W}\}(W-w[n]\geqq 0)\\
V_{n-1,W}\hspace{111pt}(W-w[n]<0)
\end{cases}
| 3 | 5 |
| 2 | 3 |
| 1 | 4 |
| 3 | 4 |
w_i
v_i
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | |||||||
| 0 | |||||||
| 0 | |||||||
| 0 |
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
| 0 | ||||||||
| 1 | ||||||||
| 2 | ||||||||
| 3 | ||||||||
| 4 |
i
j
n
W
取る時、\((i-1,j-w[i])\)から遷移
取らない時、\((i-1,j)\)から遷移
重さがオーバーしてて取れない( 欄外 )
\(-2\)
解法３：もらうDP：図
V_{n,W}
= \begin{cases} \max\{ V_{n-1,W-w[n]}+v[n],V_{n-1,W}\}(W-w[n]\geqq 0)\\
V_{n-1,W}\hspace{111pt}(W-w[n]<0)
\end{cases}
| 3 | 5 |
| 2 | 3 |
| 1 | 4 |
| 3 | 4 |
w_i
v_i
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | |||||||
| 0 | |||||||
| 0 | |||||||
| 0 |
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
| 0 | ||||||||
| 1 | ||||||||
| 2 | ||||||||
| 3 | ||||||||
| 4 |
i
j
n
W
取る時、\((i-1,j-w[i])\)から遷移
取らない時、\((i-1,j)\)から遷移
重さがオーバーしてて取れない( 欄外 )
\(-2\)
解法３：もらうDP：図
V_{n,W}
= \begin{cases} \max\{ V_{n-1,W-w[n]}+v[n],V_{n-1,W}\}(W-w[n]\geqq 0)\\
V_{n-1,W}\hspace{111pt}(W-w[n]<0)
\end{cases}
| 3 | 5 |
| 2 | 3 |
| 1 | 4 |
| 3 | 4 |
w_i
v_i
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | ||||||
| 0 | |||||||
| 0 | |||||||
| 0 |
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
| 0 | ||||||||
| 1 | ||||||||
| 2 | ||||||||
| 3 | ||||||||
| 4 |
i
j
n
W
取る時、\((i-1,j-w[i])\)から遷移
取らない時、\((i-1,j)\)から遷移
重さがオーバーしてて取れない( 欄外 )
\(-2\)
解法３：もらうDP：図
V_{n,W}
= \begin{cases} \max\{ V_{n-1,W-w[n]}+v[n],V_{n-1,W}\}(W-w[n]\geqq 0)\\
V_{n-1,W}\hspace{111pt}(W-w[n]<0)
\end{cases}
| 3 | 5 |
| 2 | 3 |
| 1 | 4 |
| 3 | 4 |
w_i
v_i
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | ||||||
| 0 | |||||||
| 0 | |||||||
| 0 |
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
| 0 | ||||||||
| 1 | ||||||||
| 2 | ||||||||
| 3 | ||||||||
| 4 |
i
j
n
W
取る時、\((i-1,j-w[i])\)から遷移
取らない時、\((i-1,j)\)から遷移
重さがオーバーしてて取れない( 欄外 )
\(-1\)
解法３：もらうDP：図
V_{n,W}
= \begin{cases} \max\{ V_{n-1,W-w[n]}+v[n],V_{n-1,W}\}(W-w[n]\geqq 0)\\
V_{n-1,W}\hspace{111pt}(W-w[n]<0)
\end{cases}
| 3 | 5 |
| 2 | 3 |
| 1 | 4 |
| 3 | 4 |
w_i
v_i
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | ||||||
| 0 | |||||||
| 0 | |||||||
| 0 |
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
| 0 | ||||||||
| 1 | ||||||||
| 2 | ||||||||
| 3 | ||||||||
| 4 |
i
j
n
W
取る時、\((i-1,j-w[i])\)から遷移
取らない時、\((i-1,j)\)から遷移
重さがオーバーしてて取れない( 欄外 )
\(-1\)
解法３：もらうDP：図
V_{n,W}
= \begin{cases} \max\{ V_{n-1,W-w[n]}+v[n],V_{n-1,W}\}(W-w[n]\geqq 0)\\
V_{n-1,W}\hspace{111pt}(W-w[n]<0)
\end{cases}
| 3 | 5 |
| 2 | 3 |
| 1 | 4 |
| 3 | 4 |
w_i
v_i
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | |||||
| 0 | |||||||
| 0 | |||||||
| 0 |
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
| 0 | ||||||||
| 1 | ||||||||
| 2 | ||||||||
| 3 | ||||||||
| 4 |
i
j
n
W
取る時、\((i-1,j-w[i])\)から遷移
取らない時、\((i-1,j)\)から遷移
重さがオーバーしてて取れない( 欄外 )
\(-1\)
解法３：もらうDP：図
V_{n,W}
= \begin{cases} \max\{ V_{n-1,W-w[n]}+v[n],V_{n-1,W}\}(W-w[n]\geqq 0)\\
V_{n-1,W}\hspace{111pt}(W-w[n]<0)
\end{cases}
| 3 | 5 |
| 2 | 3 |
| 1 | 4 |
| 3 | 4 |
w_i
v_i
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | |||||
| 0 | |||||||
| 0 | |||||||
| 0 |
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
| 0 | ||||||||
| 1 | ||||||||
| 2 | ||||||||
| 3 | ||||||||
| 4 |
i
j
n
W
取る時、\((i-1,j-w[i])\)から遷移
取らない時、\((i-1,j)\)から遷移
解法３：もらうDP：図
V_{n,W}
= \begin{cases} \max\{ V_{n-1,W-w[n]}+v[n],V_{n-1,W}\}(W-w[n]\geqq 0)\\
V_{n-1,W}\hspace{111pt}(W-w[n]<0)
\end{cases}
| 3 | 5 |
| 2 | 3 |
| 1 | 4 |
| 3 | 4 |
w_i
v_i
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | |||||
| 0 | |||||||
| 0 | |||||||
| 0 |
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
| 0 | ||||||||
| 1 | ||||||||
| 2 | ||||||||
| 3 | ||||||||
| 4 |
i
j
n
W
取る時、\((i-1,j-w[i])\)から遷移
取らない時、\((i-1,j)\)から遷移
+5
解法３：もらうDP：図
V_{n,W}
= \begin{cases} \max\{ V_{n-1,W-w[n]}+v[n],V_{n-1,W}\}(W-w[n]\geqq 0)\\
V_{n-1,W}\hspace{111pt}(W-w[n]<0)
\end{cases}
| 3 | 5 |
| 2 | 3 |
| 1 | 4 |
| 3 | 4 |
w_i
v_i
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | |||||
| 0 | |||||||
| 0 | |||||||
| 0 |
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
| 0 | ||||||||
| 1 | ||||||||
| 2 | ||||||||
| 3 | ||||||||
| 4 |
i
j
n
W
取る時、\((i-1,j-w[i])\)から遷移
取らない時、\((i-1,j)\)から遷移
+5
0+5と0の大きい方を取る
解法３：もらうDP：図
V_{n,W}
= \begin{cases} \max\{ V_{n-1,W-w[n]}+v[n],V_{n-1,W}\}(W-w[n]\geqq 0)\\
V_{n-1,W}\hspace{111pt}(W-w[n]<0)
\end{cases}
| 3 | 5 |
| 2 | 3 |
| 1 | 4 |
| 3 | 4 |
w_i
v_i
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 5 | ||||
| 0 | |||||||
| 0 | |||||||
| 0 |
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
| 0 | ||||||||
| 1 | ||||||||
| 2 | ||||||||
| 3 | ||||||||
| 4 |
i
j
n
W
取る時、\((i-1,j-w[i])\)から遷移
取らない時、\((i-1,j)\)から遷移
+5
0+5と0の大きい方を取る
解法３：もらうDP：図
V_{n,W}
= \begin{cases} \max\{ V_{n-1,W-w[n]}+v[n],V_{n-1,W}\}(W-w[n]\geqq 0)\\
V_{n-1,W}\hspace{111pt}(W-w[n]<0)
\end{cases}
| 3 | 5 |
| 2 | 3 |
| 1 | 4 |
| 3 | 4 |
w_i
v_i
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 5 | ||||
| 0 | |||||||
| 0 | |||||||
| 0 |
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
| 0 | ||||||||
| 1 | ||||||||
| 2 | ||||||||
| 3 | ||||||||
| 4 |
i
j
n
W
取る時、\((i-1,j-w[i])\)から遷移
取らない時、\((i-1,j)\)から遷移
+5
0+5と0の大きい方を取る
解法３：もらうDP：図
V_{n,W}
= \begin{cases} \max\{ V_{n-1,W-w[n]}+v[n],V_{n-1,W}\}(W-w[n]\geqq 0)\\
V_{n-1,W}\hspace{111pt}(W-w[n]<0)
\end{cases}
| 3 | 5 |
| 2 | 3 |
| 1 | 4 |
| 3 | 4 |
w_i
v_i
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 5 | 5 | |||
| 0 | |||||||
| 0 | |||||||
| 0 |
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
| 0 | ||||||||
| 1 | ||||||||
| 2 | ||||||||
| 3 | ||||||||
| 4 |
i
j
n
W
取る時、\((i-1,j-w[i])\)から遷移
取らない時、\((i-1,j)\)から遷移
+5
0+5と0の大きい方を取る
解法３：もらうDP：図
V_{n,W}
= \begin{cases} \max\{ V_{n-1,W-w[n]}+v[n],V_{n-1,W}\}(W-w[n]\geqq 0)\\
V_{n-1,W}\hspace{111pt}(W-w[n]<0)
\end{cases}
| 3 | 5 |
| 2 | 3 |
| 1 | 4 |
| 3 | 4 |
w_i
v_i
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 5 | 5 | 5 | 5 | 5 |
| 0 | |||||||
| 0 | |||||||
| 0 |
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
| 0 | ||||||||
| 1 | ||||||||
| 2 | ||||||||
| 3 | ||||||||
| 4 |
i
j
n
W
取る時、\((i-1,j-w[i])\)から遷移
取らない時、\((i-1,j)\)から遷移
解法３：もらうDP：図
V_{n,W}
= \begin{cases} \max\{ V_{n-1,W-w[n]}+v[n],V_{n-1,W}\}(W-w[n]\geqq 0)\\
V_{n-1,W}\hspace{111pt}(W-w[n]<0)
\end{cases}
| 3 | 5 |
| 2 | 3 |
| 1 | 4 |
| 3 | 4 |
w_i
v_i
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 5 | 5 | 5 | 5 | 5 |
| 0 | |||||||
| 0 | |||||||
| 0 |
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
| 0 | ||||||||
| 1 | ||||||||
| 2 | ||||||||
| 3 | ||||||||
| 4 |
i
j
n
W
取る時、\((i-1,j-w[i])\)から遷移
取らない時、\((i-1,j)\)から遷移
解法３：もらうDP：図
V_{n,W}
= \begin{cases} \max\{ V_{n-1,W-w[n]}+v[n],V_{n-1,W}\}(W-w[n]\geqq 0)\\
V_{n-1,W}\hspace{111pt}(W-w[n]<0)
\end{cases}
| 3 | 5 |
| 2 | 3 |
| 1 | 4 |
| 3 | 4 |
w_i
v_i
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 5 | 5 | 5 | 5 | 5 |
| 0 | |||||||
| 0 | |||||||
| 0 |
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
| 0 | ||||||||
| 1 | ||||||||
| 2 | ||||||||
| 3 | ||||||||
| 4 |
i
j
n
W
取る時、\((i-1,j-w[i])\)から遷移
取らない時、\((i-1,j)\)から遷移
解法３：もらうDP：図
V_{n,W}
= \begin{cases} \max\{ V_{n-1,W-w[n]}+v[n],V_{n-1,W}\}(W-w[n]\geqq 0)\\
V_{n-1,W}\hspace{111pt}(W-w[n]<0)
\end{cases}
| 3 | 5 |
| 2 | 3 |
| 1 | 4 |
| 3 | 4 |
w_i
v_i
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 5 | 5 | 5 | 5 | 5 |
| 0 | 0 | ||||||
| 0 | |||||||
| 0 |
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
| 0 | ||||||||
| 1 | ||||||||
| 2 | ||||||||
| 3 | ||||||||
| 4 |
i
j
n
W
取る時、\((i-1,j-w[i])\)から遷移
取らない時、\((i-1,j)\)から遷移
解法３：もらうDP：図
V_{n,W}
= \begin{cases} \max\{ V_{n-1,W-w[n]}+v[n],V_{n-1,W}\}(W-w[n]\geqq 0)\\
V_{n-1,W}\hspace{111pt}(W-w[n]<0)
\end{cases}
| 3 | 5 |
| 2 | 3 |
| 1 | 4 |
| 3 | 4 |
w_i
v_i
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 5 | 5 | 5 | 5 | 5 |
| 0 | 0 | ||||||
| 0 | |||||||
| 0 |
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
| 0 | ||||||||
| 1 | ||||||||
| 2 | ||||||||
| 3 | ||||||||
| 4 |
i
j
n
W
取る時、\((i-1,j-w[i])\)から遷移
取らない時、\((i-1,j)\)から遷移
解法３：もらうDP：図
V_{n,W}
= \begin{cases} \max\{ V_{n-1,W-w[n]}+v[n],V_{n-1,W}\}(W-w[n]\geqq 0)\\
V_{n-1,W}\hspace{111pt}(W-w[n]<0)
\end{cases}
| 3 | 5 |
| 2 | 3 |
| 1 | 4 |
| 3 | 4 |
w_i
v_i
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 5 | 5 | 5 | 5 | 5 |
| 0 | 0 | ||||||
| 0 | |||||||
| 0 |
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
| 0 | ||||||||
| 1 | ||||||||
| 2 | ||||||||
| 3 | ||||||||
| 4 |
i
j
n
W
取る時、\((i-1,j-w[i])\)から遷移
取らない時、\((i-1,j)\)から遷移
+3
0+3と0の大きい方を取る
解法３：もらうDP：図
V_{n,W}
= \begin{cases} \max\{ V_{n-1,W-w[n]}+v[n],V_{n-1,W}\}(W-w[n]\geqq 0)\\
V_{n-1,W}\hspace{111pt}(W-w[n]<0)
\end{cases}
| 3 | 5 |
| 2 | 3 |
| 1 | 4 |
| 3 | 4 |
w_i
v_i
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 5 | 5 | 5 | 5 | 5 |
| 0 | 0 | 3 | |||||
| 0 | |||||||
| 0 |
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
| 0 | ||||||||
| 1 | ||||||||
| 2 | ||||||||
| 3 | ||||||||
| 4 |
i
j
n
W
取る時、\((i-1,j-w[i])\)から遷移
取らない時、\((i-1,j)\)から遷移
+3
0+3と0の大きい方を取る
解法３：もらうDP：図
V_{n,W}
= \begin{cases} \max\{ V_{n-1,W-w[n]}+v[n],V_{n-1,W}\}(W-w[n]\geqq 0)\\
V_{n-1,W}\hspace{111pt}(W-w[n]<0)
\end{cases}
| 3 | 5 |
| 2 | 3 |
| 1 | 4 |
| 3 | 4 |
w_i
v_i
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 5 | 5 | 5 | 5 | 5 |
| 0 | 0 | 3 | |||||
| 0 | |||||||
| 0 |
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
| 0 | ||||||||
| 1 | ||||||||
| 2 | ||||||||
| 3 | ||||||||
| 4 |
i
j
n
W
取る時、\((i-1,j-w[i])\)から遷移
取らない時、\((i-1,j)\)から遷移
+3
0+3と5の大きい方を取る
解法３：もらうDP：図
V_{n,W}
= \begin{cases} \max\{ V_{n-1,W-w[n]}+v[n],V_{n-1,W}\}(W-w[n]\geqq 0)\\
V_{n-1,W}\hspace{111pt}(W-w[n]<0)
\end{cases}
| 3 | 5 |
| 2 | 3 |
| 1 | 4 |
| 3 | 4 |
w_i
v_i
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 5 | 5 | 5 | 5 | 5 |
| 0 | 0 | 3 | 5 | ||||
| 0 | |||||||
| 0 |
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
| 0 | ||||||||
| 1 | ||||||||
| 2 | ||||||||
| 3 | ||||||||
| 4 |
i
j
n
W
取る時、\((i-1,j-w[i])\)から遷移
取らない時、\((i-1,j)\)から遷移
+3
0+3と5の大きい方を取る
解法３：もらうDP：図
V_{n,W}
= \begin{cases} \max\{ V_{n-1,W-w[n]}+v[n],V_{n-1,W}\}(W-w[n]\geqq 0)\\
V_{n-1,W}\hspace{111pt}(W-w[n]<0)
\end{cases}
| 3 | 5 |
| 2 | 3 |
| 1 | 4 |
| 3 | 4 |
w_i
v_i
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 5 | 5 | 5 | 5 | 5 |
| 0 | 0 | 3 | 5 | ||||
| 0 | |||||||
| 0 |
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
| 0 | ||||||||
| 1 | ||||||||
| 2 | ||||||||
| 3 | ||||||||
| 4 |
i
j
n
W
取る時、\((i-1,j-w[i])\)から遷移
取らない時、\((i-1,j)\)から遷移
+3
0+3と5の大きい方を取る
解法３：もらうDP：図
V_{n,W}
= \begin{cases} \max\{ V_{n-1,W-w[n]}+v[n],V_{n-1,W}\}(W-w[n]\geqq 0)\\
V_{n-1,W}\hspace{111pt}(W-w[n]<0)
\end{cases}
| 3 | 5 |
| 2 | 3 |
| 1 | 4 |
| 3 | 4 |
w_i
v_i
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 5 | 5 | 5 | 5 | 5 |
| 0 | 0 | 3 | 5 | 5 | |||
| 0 | |||||||
| 0 |
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
| 0 | ||||||||
| 1 | ||||||||
| 2 | ||||||||
| 3 | ||||||||
| 4 |
i
j
n
W
取る時、\((i-1,j-w[i])\)から遷移
取らない時、\((i-1,j)\)から遷移
+3
0+3と5の大きい方を取る
解法３：もらうDP：図
V_{n,W}
= \begin{cases} \max\{ V_{n-1,W-w[n]}+v[n],V_{n-1,W}\}(W-w[n]\geqq 0)\\
V_{n-1,W}\hspace{111pt}(W-w[n]<0)
\end{cases}
| 3 | 5 |
| 2 | 3 |
| 1 | 4 |
| 3 | 4 |
w_i
v_i
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 5 | 5 | 5 | 5 | 5 |
| 0 | 0 | 3 | 5 | 5 | |||
| 0 | |||||||
| 0 |
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
| 0 | ||||||||
| 1 | ||||||||
| 2 | ||||||||
| 3 | ||||||||
| 4 |
i
j
n
W
取る時、\((i-1,j-w[i])\)から遷移
取らない時、\((i-1,j)\)から遷移
+3
5+3と5の大きい方を取る
解法３：もらうDP：図
V_{n,W}
= \begin{cases} \max\{ V_{n-1,W-w[n]}+v[n],V_{n-1,W}\}(W-w[n]\geqq 0)\\
V_{n-1,W}\hspace{111pt}(W-w[n]<0)
\end{cases}
| 3 | 5 |
| 2 | 3 |
| 1 | 4 |
| 3 | 4 |
w_i
v_i
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 5 | 5 | 5 | 5 | 5 |
| 0 | 0 | 3 | 5 | 5 | 8 | ||
| 0 | |||||||
| 0 |
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
| 0 | ||||||||
| 1 | ||||||||
| 2 | ||||||||
| 3 | ||||||||
| 4 |
i
j
n
W
取る時、\((i-1,j-w[i])\)から遷移
取らない時、\((i-1,j)\)から遷移
+3
5+3と5の大きい方を取る
解法３：もらうDP：図
V_{n,W}
= \begin{cases} \max\{ V_{n-1,W-w[n]}+v[n],V_{n-1,W}\}(W-w[n]\geqq 0)\\
V_{n-1,W}\hspace{111pt}(W-w[n]<0)
\end{cases}
| 3 | 5 |
| 2 | 3 |
| 1 | 4 |
| 3 | 4 |
w_i
v_i
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 5 | 5 | 5 | 5 | 5 |
| 0 | 0 | 3 | 5 | 5 | 8 | ||
| 0 | |||||||
| 0 |
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
| 0 | ||||||||
| 1 | ||||||||
| 2 | ||||||||
| 3 | ||||||||
| 4 |
i
j
n
W
取る時、\((i-1,j-w[i])\)から遷移
取らない時、\((i-1,j)\)から遷移
+3
5+3と5の大きい方を取る
解法３：もらうDP：図
V_{n,W}
= \begin{cases} \max\{ V_{n-1,W-w[n]}+v[n],V_{n-1,W}\}(W-w[n]\geqq 0)\\
V_{n-1,W}\hspace{111pt}(W-w[n]<0)
\end{cases}
| 3 | 5 |
| 2 | 3 |
| 1 | 4 |
| 3 | 4 |
w_i
v_i
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 5 | 5 | 5 | 5 | 5 |
| 0 | 0 | 3 | 5 | 5 | 8 | 8 | |
| 0 | |||||||
| 0 |
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
| 0 | ||||||||
| 1 | ||||||||
| 2 | ||||||||
| 3 | ||||||||
| 4 |
i
j
n
W
取る時、\((i-1,j-w[i])\)から遷移
取らない時、\((i-1,j)\)から遷移
+3
5+3と5の大きい方を取る
解法３：もらうDP：図
V_{n,W}
= \begin{cases} \max\{ V_{n-1,W-w[n]}+v[n],V_{n-1,W}\}(W-w[n]\geqq 0)\\
V_{n-1,W}\hspace{111pt}(W-w[n]<0)
\end{cases}
| 3 | 5 |
| 2 | 3 |
| 1 | 4 |
| 3 | 4 |
w_i
v_i
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 5 | 5 | 5 | 5 | 5 |
| 0 | 0 | 3 | 5 | 5 | 8 | 8 | 8 |
| 0 | |||||||
| 0 |
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
| 0 | ||||||||
| 1 | ||||||||
| 2 | ||||||||
| 3 | ||||||||
| 4 |
i
j
n
W
取る時、\((i-1,j-w[i])\)から遷移
取らない時、\((i-1,j)\)から遷移
5+3と5の大きい方を取る
解法３：もらうDP：図
V_{n,W}
= \begin{cases} \max\{ V_{n-1,W-w[n]}+v[n],V_{n-1,W}\}(W-w[n]\geqq 0)\\
V_{n-1,W}\hspace{111pt}(W-w[n]<0)
\end{cases}
| 3 | 5 |
| 2 | 3 |
| 1 | 4 |
| 3 | 4 |
w_i
v_i
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 5 | 5 | 5 | 5 | 5 |
| 0 | 0 | 3 | 5 | 5 | 8 | 8 | 8 |
| 0 | |||||||
| 0 |
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
| 0 | ||||||||
| 1 | ||||||||
| 2 | ||||||||
| 3 | ||||||||
| 4 |
i
j
n
W
取る時、\((i-1,j-w[i])\)から遷移
取らない時、\((i-1,j)\)から遷移
5+3と5の大きい方を取る
解法３：もらうDP：図
V_{n,W}
= \begin{cases} \max\{ V_{n-1,W-w[n]}+v[n],V_{n-1,W}\}(W-w[n]\geqq 0)\\
V_{n-1,W}\hspace{111pt}(W-w[n]<0)
\end{cases}
| 3 | 5 |
| 2 | 3 |
| 1 | 4 |
| 3 | 4 |
w_i
v_i
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 5 | 5 | 5 | 5 | 5 |
| 0 | 0 | 3 | 5 | 5 | 8 | 8 | 8 |
| 0 | |||||||
| 0 |
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
| 0 | ||||||||
| 1 | ||||||||
| 2 | ||||||||
| 3 | ||||||||
| 4 |
i
j
n
W
取る時、\((i-1,j-w[i])\)から遷移
取らない時、\((i-1,j)\)から遷移
+4
0+4と0の大きい方を取る
解法３：もらうDP：図
V_{n,W}
= \begin{cases} \max\{ V_{n-1,W-w[n]}+v[n],V_{n-1,W}\}(W-w[n]\geqq 0)\\
V_{n-1,W}\hspace{111pt}(W-w[n]<0)
\end{cases}
| 3 | 5 |
| 2 | 3 |
| 1 | 4 |
| 3 | 4 |
w_i
v_i
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 5 | 5 | 5 | 5 | 5 |
| 0 | 0 | 3 | 5 | 5 | 8 | 8 | 8 |
| 0 | 4 | ||||||
| 0 |
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
| 0 | ||||||||
| 1 | ||||||||
| 2 | ||||||||
| 3 | ||||||||
| 4 |
i
j
n
W
取る時、\((i-1,j-w[i])\)から遷移
取らない時、\((i-1,j)\)から遷移
+4
0+4と0の大きい方を取る
解法３：もらうDP：図
V_{n,W}
= \begin{cases} \max\{ V_{n-1,W-w[n]}+v[n],V_{n-1,W}\}(W-w[n]\geqq 0)\\
V_{n-1,W}\hspace{111pt}(W-w[n]<0)
\end{cases}
| 3 | 5 |
| 2 | 3 |
| 1 | 4 |
| 3 | 4 |
w_i
v_i
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 5 | 5 | 5 | 5 | 5 |
| 0 | 0 | 3 | 5 | 5 | 8 | 8 | 8 |
| 0 | 4 | 4 | 7 | 9 | 9 | 12 | 12 |
| 0 |
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
| 0 | ||||||||
| 1 | ||||||||
| 2 | ||||||||
| 3 | ||||||||
| 4 |
i
j
n
W
取る時、\((i-1,j-w[i])\)から遷移
取らない時、\((i-1,j)\)から遷移
解法３：もらうDP：図
V_{n,W}
= \begin{cases} \max\{ V_{n-1,W-w[n]}+v[n],V_{n-1,W}\}(W-w[n]\geqq 0)\\
V_{n-1,W}\hspace{111pt}(W-w[n]<0)
\end{cases}
| 3 | 5 |
| 2 | 3 |
| 1 | 4 |
| 3 | 4 |
w_i
v_i
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 5 | 5 | 5 | 5 | 5 |
| 0 | 0 | 3 | 5 | 5 | 8 | 8 | 8 |
| 0 | 4 | 4 | 7 | 9 | 9 | 12 | 12 |
| 0 | 4 | 4 | 7 | 9 | 9 | 12 | 13 |
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
| 0 | ||||||||
| 1 | ||||||||
| 2 | ||||||||
| 3 | ||||||||
| 4 |
i
j
n
W
取る時、\((i-1,j-w[i])\)から遷移
取らない時、\((i-1,j)\)から遷移
解法３：もらうDP：図
V_{n,W}
= \begin{cases} \max\{ V_{n-1,W-w[n]}+v[n],V_{n-1,W}\}(W-w[n]\geqq 0)\\
V_{n-1,W}\hspace{111pt}(W-w[n]<0)
\end{cases}
| 3 | 5 |
| 2 | 3 |
| 1 | 4 |
| 3 | 4 |
w_i
v_i
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 5 | 5 | 5 | 5 | 5 |
| 0 | 0 | 3 | 5 | 5 | 8 | 8 | 8 |
| 0 | 4 | 4 | 7 | 9 | 9 | 12 | 12 |
| 0 | 4 | 4 | 7 | 9 | 9 | 12 | 13 |
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
| 0 | ||||||||
| 1 | ||||||||
| 2 | ||||||||
| 3 | ||||||||
| 4 |
i
j
n
W
取る時、\((i-1,j-w[i])\)から遷移
取らない時、\((i-1,j)\)から遷移
答え！！
解法３：もらうDPのコード例
vector<int> w,v; //mainで入力
int given_dp(int n,int W){
vector<vector<int>> dp(n+1,vector<int>(W+1));
//初項の設定
for(int i=0;i<=n;++i) dp[i][0] = 0;
for(int i=0;i<=W;++i) dp[0][i] = 0;
//遷移の実行
for(int i=1;i<=n;++i){ //nについてのループ
for(int j=1;j<=W;++j){ //Wについてのループ
if(j-w[i-1]<0) dp[i][j] = dp[i-1][j];
else dp[i][j] = max(dp[i-1][j],dp[i-1][j-w[i-1]]+v[i-1]);
}
}
//答えは配列dpのここ
return dp[n][W];
}
解法３：もらうDPの考察
- 自明だった例題１と異なり、結構むずい。
- \(O(nW)\)
- ただ、再帰を使わない上、計算量に近似が含まれないので、こっちの方がメモ化再帰より速い。(再帰は重い)
- 考察はむずいが実装はメモ化再帰より簡単。
- どっちが良いかは好みだと思う。
例題２：ナップサック問題
配るDP
配るDPしたい！
- もらうDPは確定した場所から値をもらう。
- 配るDPは逆に確定した場所から値を配る。
- 問題の分割方法はもらうDPと同じ。
- なので、さっきの\(V_{n,W}\)を使い、\(V_{0,j}=0\), \(V_{i,0}=0\)
- というわけでこの遷移について考えてみる。
配るDPしたい！
- 遷移は、今見てる確定済みの値から、どこに影響を及ぼすかについて考えれば良い。
- （\(\to\)は影響を与えるという意味）
- 品物\(n+1\)を取る時、
\(V_{n,W}\to V_{n+1,W+w[n+1]}\)
- 品物\(n+1\)を取らない時、
\(V_{n,W}\to V_{n+1,W}\)
- これで遷移元と遷移先は確定した。
解法４：配るDP
- 遷移によって配られたものの最大値を取れば良い。
- 予め、\(V\)を\(\max\)の単位元として0で全て埋めておいて、
- 品物\(n+1\)を取る時、
\(V_{n+1,W+w[n+1]}\\=\max\{V_{n+1,W+w[n+1]},V_{n,W}+v[n+1]\}\)
- 品物\(n+1\)を取らない時、
\(V_{n+1,W}=\max\{V_{n+1,W},V_{n,W}\}\)
- もちろん、品物\(n+1\)がそもそも取れない時は場合分けする。
解法４：配るDPのコード
vector<int> w,v; //mainで入力
int dp_dist(int n,int W){
//最初は全部0で初期化
vector<vector<int>> dp(n+1,vector<int>(W+1,0));
for(int i=0;i<n;++i){
for(int j=0;j<=W;++j){
if(j+w[i]<=W){ //取れる時
dp[i+1][j+w[i]]
=max(dp[i+1][j+w[i]],dp[i][j]+v[i]);
}
//取らない時
dp[i+1][j] = max(dp[i+1][j],dp[i][j]);
}
}
return dp[n][W];
}解法４：配るDPの考察
- \(O(nW)\)
- もらうDPを逆から見た感じ。
- 計算量、実装のメモ化再帰との比較はだいたいもらうDPと同じなので割愛。
- 例題２はもらうDPとそんなに難易度差はないかな。
- さっきも言ったけど、どっちの方が楽かは問題によるので、いい感じに使い分けよう。
"もらう"と"配る"の違い
- もらうDPは、確定した、今見てる場所より手前の値から、今の値への遷移を考えるDP。
- 配るDPは、確定した今見てる値から、未確定の先の値への遷移を考えるDP。
まとめ
DPの使い分け
- メモ化再帰
- 実装がやや面倒
- 計算量がやや重い
- 考察は楽
- もらうDP, 配るDP
- 考察が面倒
- 実装は楽
- 計算量も軽め
- いい感じにそれぞれ使い分けよう！
- 慣れない内はメモ化再帰で良いと思う。
参考文献
- プログラミングコンテストチャレンジブック第二版
- 通称 蟻本。
- アルゴリズムのあれこれが載ってます。
- 競プロerのほとんどが持っている。
- 競プロやるなら、買って損はないと思います。
- 去年のスライド
お知らせ
-
新歓コンパ！！！
- 明日！！！！！！！
- 楽しもう！！！！
- (参加表明の締め切りは過ぎてます)
次回予告
- 次回は5/24(金) 互除法とか数学的なあれこれ
- 百万遍に部員がくるサービスはもう終了なので、次回は18:30に直接部室に集合！！！
- 部室の場所分からない人いますか？
コンテスト
- コンテスト中にスライドを見たり、ググったりしてくれて全然良いです。
- 分からないことがあれば僕に質問してもOK
- コンテストページは内部Wikiにもあるよ。