Functions

Functions are "self contained" modules of code that accomplish a specific task.

Why to write functions?

They allow us to conceive of our program as a bunch of sub-steps.
They allow us to reuse code instead of rewriting it.

Syntax of writing a function

<return type> <function name>([<argument1>,<argument2>,..]) {
    statement 1;
    statement 2;
    .
    .
    
    return <return value>;
}

Examples of functions

boolean prime(int num){
    boolean flag=true;
    int i=1;
    if(num==1)
        return false;
    else if(num==2)
        return flag;
    for(i=3;i<num;++i){
        if(num%i==0)
            return false;
    }
    return flag;
}

Using this function

#include<stdio.h>
boolean prime(int num);
void main(){
    printf("Enter a number");
    scanf("%d",&no);
    ch=prime(no);
    if(ch)
        printf("The number is prime");
    else
        printf("The number is not prime");
}
boolean prime(int num){
    boolean flag=true;
    int i=1;
    if(num==1)
        return false;
    else if(num==2)
        return flag;
    for(i=3;i<num;++i){
        if(num%i==0)
            return false;
    }
    return flag;
}

Exercising Examples

We are given two numbers as input and we have to find all the prime numbers between them.

Input : Two numbers.

Output : All the prime numbers between them.

#include<stdio.h>
boolean prime(int num);
int main(){
   int n1,n2,i,flag;
   printf("Enter two numbers(intervals): ");
   scanf("%d %d",&n1, &n2);
   printf("Prime numbers between %d and %d are: ", n1, n2);
   for(i=n1+1;i<n2;++i)
   {
      flag=prime(i);
      if(flag)
         printf("%d ",i);
   }
   return 0;
}
boolean prime(int num){
    boolean flag=true;
    int i=1;
    if(num==1)
        return false;
    else if(num==2)
        return flag;
    for(i=3;i<num;++i){
        if(num%i==0)
            return false;
    }
    return flag;
}

A program to convert binary number into decimal or decimal number to binary.

Input : A character either 'd' indicating given number is in binary and convert into decimal or 'b' stating reverse.

Output : Number in changed representation.

#include <stdio.h>
#include <math.h>
int binary_decimal(int n);
int decimal_binary(int n);
int main()
{
   int n;
   char c;
   scanf("%c",&c);
   if (c =='d' || c == 'D')
   {
       printf("Enter a binary number: ");
       scanf("%d", &n);
       printf("%d in binary = %d in decimal", n, binary_decimal(n));
   }
   if (c =='b' || c == 'B')
   {
       printf("Enter a decimal number: ");
       scanf("%d", &n);
       printf("%d in decimal = %d in binary", n, decimal_binary(n));
   }
   return 0;
}

int decimal_binary(int n)  /* Function to convert decimal to binary.*/
{
    int rem, i=1, binary=0;
    while (n!=0)
    {
        rem=n%2;
        n/=2;
        binary+=rem*i;
        i*=10;
    }
    return binary;
}

int binary_decimal(int n) /* Function to convert binary to decimal.*/

{
    int decimal=0, i=0, rem;
    while (n!=0)
    {
        rem = n%10;
        n/=10;
        decimal += rem*pow(2,i);
        ++i;
    }
    return decimal;
}

Recursion

Recursion is the process of repeating items in a self-similar way.

For example :

f(n)=f(n-1)+n
f(n)=f(n-1)*n
f(n)=f(n-1)+f(n-2)

In Computer Science

Recursion is the process a procedure goes through when one of the steps of the procedure involves invoking the procedure itself.

Simply, when a function calls itself.

Coding for f(n)=f(n-1)*n

Factorial

#include<stdio.h>
int fact(int num);
void main(){
    int no,factorial;
    scanf("%d",&no);
    factorial=fact(no);
    printf("Factorial of the number is %d",&factorial);
}

int fact(int num){
    if(num==1 || num==0)
        return 1;
    return num*fact(num-1);
}

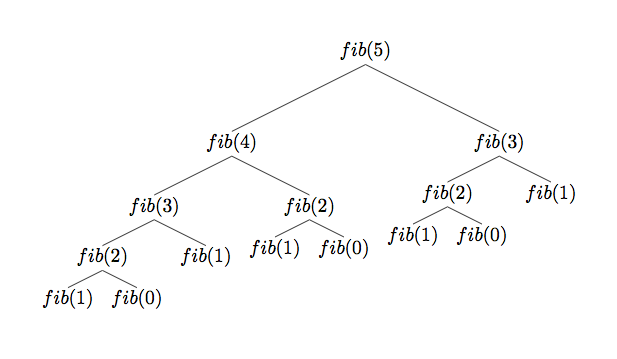
Fibonacci numbers

0,1,1,2,3,5,8,13,21,34,55,89,...

F(n)=F(n-1)+F(n-2)

int fibo(int num){
    if(num==1)
        return 0;
    if(num==2)
        return 1;
    return fibo(num-1)+fibo(num-2);
}

Divide and Conquer

A divide and conquer algorithm works by recursively breaking down a problem into two or more sub-problems of the same (or related) type, until these become simple enough to be solved directly.

Generally contains three steps

Divide : Break the problem into sub problems of same type.
Conquer : Solve the problems recursively
Combine (Merge) : Appropriately combine the

Searching an element in sorted array

Just traverse the array and check whether it is present or not.

Wait, since we know the array is sorted

We will check the middle element of the array and check whether its the required number or its less than or greater than the number.

We can repeat the process and do it much faster.

The method is called Binary Search and take O(log n) time.

If it is less, then we have to traverse only the right half of the array.

If it is more, then we have to traverse only the left half of the array.

If its equal to the number Congrats, you are lucky.

Merge Sort

It is based on divide and conquer paradigm and sorts in O(nlogn) time.

Dividing the problem

Merge Sort divides the array into smaller sub arrays and sort them.

Problem : Sorting the array.

Sub Problem : Sorting the sub arrays.

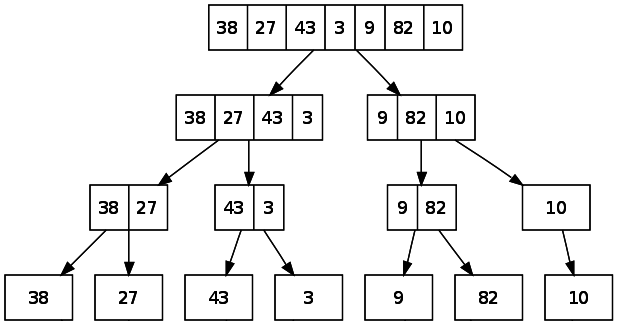
Combining the sub answers

Merge the sorted arrays in a sorted way.

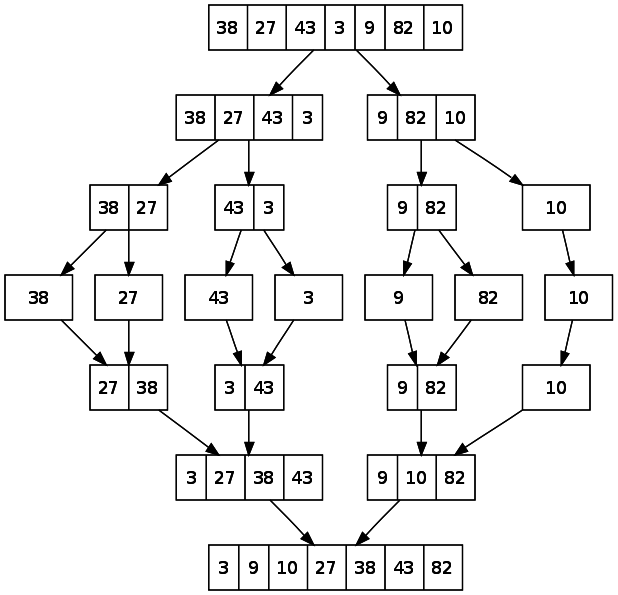
But wait, we didn't find the answers for the sub problem.

We divide till the size of the sub array is 1.

Every array of size 1 is sorted.

So, breaking the problem into sub problems results in the answers of the sub problems.

The Algorithm

Divide the problem into sub problems using recursion.

When we reach the last point of our division, we don't need to solve sub problems.

Merge them to get the final sorted array.

The Code

Make a recursive function which divides the problem into sub problems.

Make a function to merge the sorted arrays.

Counting Inversions

Inversion is pair of numbers which are not naturally ordered.

For example :

[2, 3, 1, 4] has 2 inversions.

Pairs of i and j indices where i<j and ar[i] > ar[j].

When we merge the arrays in merge sort, counting the number of elements of second part which comes before the first one in combined sorted array.

Functions

Questions