In by Out Again

Arbitrarily-Deep Zooming on Iterated Function Systems by 'Self-Similarity Jumping'

BSc Wiebe-Marten Wijnja

Summary

  • Iterated Function Systems?
  • Existing rendering methods
  • New approach
  • Results & Remarks
  • Conclusion

What is an Iterated Function System?

  • What: Mathematical concept, related to set theory and constructing fractals
  • Why: physics, image compression, gene structures, beauty
  • How:

What is an Iterated Function System?

  • What: Mathematical concept, related to set theory and constructing fractals
  • Why: physics, image compression, gene structures, beauty
  • How:

"repeatedly apply the collection of mappings"

What is an Iterated Function System?

  • What: Mathematical concept, related to set theory and constructing fractals
  • Why: physics, image compression, gene structures, beauty
  • How:

iterate

system

(transformation) functions

"repeatedly apply the collection of mappings"

Transformation function (mapping)

image \(\longrightarrow\) transformed image

image: Set of points

Transformation function (mapping)

System of functions

{

}

,

Iterate

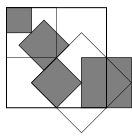
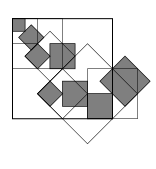
Another example

Formally

  • IFS $$ \mathcal{F} = \{ f_i : \mathcal{M} \rightarrow \mathcal{M}\}_{i=1}^N, N \in \mathbb{N}$$(mappings are required to be contractive)

  • one iteration: $$ \mathcal{S}_{n + 1} = \bigcup_{i=1}^{N} f_i(\mathcal{S}_n), n \in \mathbb{N}$$

  • Attractor: $$\mathcal{A} = \lim_{n \rightarrow \infty} \mathcal{S}_n$$

     

(\(\mathcal{S}_0 \) can be an arbitrary non-empty set of points)

Formally

  • IFS $$ \mathcal{F} = \{ f_i : \mathcal{M} \rightarrow \mathcal{M}\}_{i=1}^N, N \in \mathbb{N}$$(mappings are required to be contractive)

  • one iteration: $$ \mathcal{S}_{n + 1} = \bigcup_{i=1}^{N} f_i(\mathcal{S}_n), n \in \mathbb{N}$$

  • Attractor: $$\mathcal{A} = \lim_{n \rightarrow \infty} \mathcal{S}_n$$

     

(\(\mathcal{S}_0 \) can be an arbitrary non-empty set of points)

!!

Formally

  • IFS $$ \mathcal{F} = \{ f_i : \mathcal{M} \rightarrow \mathcal{M}\}_{i=1}^N, N \in \mathbb{N}$$(mappings are required to be contractive)

  • one iteration: $$ \mathcal{S}_{n + 1} = \bigcup_{i=1}^{N} f_i(\mathcal{S}_n), n \in \mathbb{N}$$

  • Attractor: $$\mathcal{A} = \lim_{n \rightarrow \infty} \mathcal{S}_n$$

     

(\(\mathcal{S}_0 \) can be an arbitrary non-empty set of points)

!!

👌

Rendering an IFS's attractor

\(t(t(t(\mathcal{S}_0))) \cup t(t(l(\mathcal{S}_0))) \cup \ldots r(r(r(\mathcal{S}_0)))\)

how to find all transformation-sequences?

Transformation-sequences as trees

\(t(t(t(\mathcal{S}_0))) \cup t(t(l(\mathcal{S}_0))) \cup \ldots r(r(r(\mathcal{S}_0)))\)

Depth-First

Breadth-First

  • Depth-First:
    •   \(\mathcal{O}\big(\log{P}\big)\) memory
  • Breadth-First:
    • \(\mathcal{O}\big(P\big)\) memory,
    • but able to stop interactively

Can we do better?

  • Both use quite a bit of memory
  • Difficult to parallellize (reason: coordination)*

* There is one cool (but complex) implementation,

c.f. Orion Sky Lawlor. "GPU-accelerated rendering of unbounded nonlinear iterated function system fixed points"

 

\(t(t(t(\mathcal{S}_0))) \cup t(t(l(\mathcal{S}_0))) \cup \ldots r(r(r(\mathcal{S}_0)))\)

\(t(t(t(l(\mathcal{S}_0)))) \approx t(t(t(r(\mathcal{S}_0)))) \)

[

[

indistinguishable!

\( t(t(t(\ldots)))) \rightarrow r(t(t(t(\ldots))))) \rightarrow t(r(t(t(t(\ldots)))))) \rightarrow l(t(r(t(t(t(\ldots)))))))  \) etc.

[

[

[

[

ttt, rtt, trt, ltr, etc.

Yes!

  • \(\mathcal{O}(1)\) memory
  • Simple implementation
    • including a parallel one
  • but needs
    • enough points
    • fine-tuned probabilities

the chaos game

the chaos game

  N: the number of mappings of the IFS;
  z: a single arbitrary starting point;
  v: the camera's view transformation;
  m = 0;
  for m ∈ [0..n + P) { 
    i: a random integer between 0 and N;
    if(m >= n){
      render(v(z)) cumulatively;
    }
    z = fᵢ(z);
  }

But what about animations?

New Approach

  1. Use a point cloud
    • moving the camera does not change points
  2. 'self-similarity jumping'
    • Too little detail? (ab)use self-similarity to (re)use more points!
  • Based on the Chaos Game
  • Meant for animations/interaction

Self-Similarity Jumping

Self-Similarity Jumping

"inside", "outside", "overlapping"

  n: the number of mappings the IFS consists of;
  v: the current camera's view transformation;
  s: a stack of jumps made so far;
  for i <- [1, ..., n] { 
    if isInvertible(fᵢ) and isInside(v⁻¹, fᵢ) {
      push(s, fᵢ);
      v = fᵢ⁻¹ ◦ v;
      break;
    }
  }

  v: the current camera's view transformation;
  s: a stack of jumps made until now;
  if notEmpty(s) and isOutsideUnitSquare(v⁻¹) {
    f = pop(s);
    v = f ◦ v;
  }

Jump 'up'

Jump 'down'

Implementation

  • Haskell
  • Accelerate library
    • Haskell EDSL \(\rightarrow\) LLVM \(\rightarrow\) NVidia PTX ('GPU assembly')

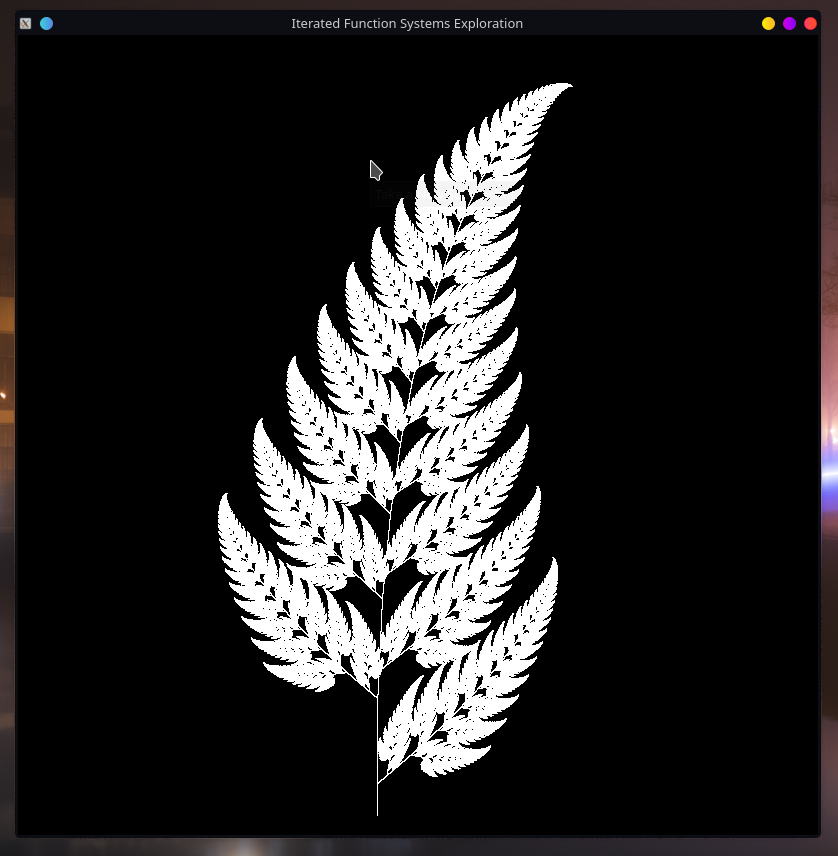
Results & Remarks

  • Point clouds take a lot of GPU memory
  • Self-similarity jumping has two restrictions

Cannot be used on 'borders'

Points of single subtransformation visible

Points of multiple subtransformations visible: problem

Both cases are unfortunately rather common

Conclusion

  • The technique works, but has limited applicability
    • point clouds take a lot of memory
    • self-similarity jumping cannot be used everywhere

Summary

  • Iterated Function Systems?
  • Existing rendering methods
  • New approach
  • Results & Remarks
  • Conclusion

Image Attribution

Thank you!

Thanks to

  • Jiří Kosinka for answering all my questions, and sheer limitless  patience
  • Luc, Jeroen, Sietze and Michiel for kindling my love for computer graphics, visualization and clever algorithms

Thank you!

Questions?

Made with Slides.com