우리가 하는 게임은
정말로 공평할까?
'^'(3511 백종천)
"갑이 주사위를 두 번 던졌을 때 을이 한번 던진 주사위의 눈이 갑이 던진 두 눈 사이일 경우 을이 승리하고 그렇지 않은 경우에는 갑이 승리하는 임의의 게임에서 을이 이길 확률은 몇일까?"
승리
패배
갑 > 을
22/27 > 5/27
우리가 평소에 하던
게임도 불공평?

목적

보편적 게임

https://t1.daumcdn.net/thumb/R720x0/?fname=http://t1.daumcdn.net/brunch/service/user/1Nyw/image/JvIG_2lFwWAOV3rbZ_091-2W2Og.jpg
가위바위보

http://res.heraldm.com/content/image/2016/06/17/20160617000234_0.jpg
모든 경우의 수
A가 낼 수 있는 형태의 수 * B가 낼 수 있는 형태의 수
= 3 * 3 = 9
A가 이기는 경우의 수
A가 낼 수 있는 형태의 수 * A에 지는 형태의 수
= 3 * 1 = 3
가정 : 사람 A, B가 있고 한번 가위바위보를 한다.
A가 이기는 확률 : 1/3
모든 경우의 수
A가 낼 수 있는 형태의 수 * B가 낼 수 있는 형태의 수
= 3 * 3 = 9
비기는 경우의 수
A가 낼 수 있는 형태의 수 * A와 같은 형태의 수
= 3 * 1 = 3
비기는 확률 : 1/3
A가 이기는 확률 : 1/3
B가 이기는 확률 : 1 - (1/3 + 1/3) = 1/3


=
두 명이서 하는 가위바위보
틱택토(tic tac toe)

https://upload.wikimedia.org/wikipedia/commons/thumb/3/32/Tic_tac_toe.svg/2000px-Tic_tac_toe.svg.png
O 승!
1. O와 X가 각각 승리하는 경우의 수
(O가 먼저 시작)
3. 전체 경우의 수 구하기
4. 확률 구하기
2. 비기는 경우의 수
1, 2, 3, 4턴 까지
게임이 끝나지 않음.
(= O, X 가 한줄이 안됨.)
5턴에서 O가 승리하는 경우

승리하는 패턴 수 * O가 표시하는 수 * X가 표시하는 수
= 8 * 3! * 6P2
= 1440
6턴에서 X가 승리하는 경우
(승리하는 패턴 수 * X가 표시하는 수 * O가 표시하는 수)
= 8 * 3! * 6P3
= 5760

6턴에서 X가 승리하는 것보다
5턴에서 먼저 O가 승리하는 경우
(대각선을 제외한 X가 이길 수 있는 패턴 * X가 앞의 패턴으로 둘 때 나머지 O가 이길 수 있는 패턴 * X가 표시하는 경우의 수 * O가 표시하는 경우의 수)
= (8 – 2) * 2 * (3 * 2) * (3!)
= 6 * 2 * 6 * 6
= 432


6턴에서 X가 승리하는 경우
(6턴에서 X가 선을 이루는 경우의 수)
- (5턴에서 O가 X보다 빠르게 선을 이루는 경우의 수)
= 5760 – 432
= 5328
7턴에서 O가 승리하는 경우

(O가 이기는 패턴의 수 * 체크 표시 중 하나를 고를 경우의 수 * 체크 표시를 선택하는 대신 지울 수 있는 패턴의 수 * 5턴까지 O를 배치하는 경우의 수)
= 8 * 6 * 3 * 3!
= 864
7턴에서 O가 승리하는 경우

(O를 표시하는 경우의 수) * (X를 표시하는 경우의 수)
= 864 * (나머지 5칸에 3개의 X를 표시하는 경우의 수)
= 864 * 5P3
= 864 * 5 * 4 * 3
= 51840
7턴에서 O가 승리하기 전에
6턴에서 X가 먼저 선을 만드는 경우
(X가 만들 수 있는 패턴의 수 * X를 표시할 경우의 수 * O가 만들 수 있는 패턴의 수 * 체크 표시 중 하나를 고를 경우의 수 * 체크 표시를 선택하는 대신 지울 수 있는 패턴의 수 * O를 표시할 경우의 수)
= (8 – 2) * 3! * 2 * 3 * 3 * 3!
= 6 * 3! * 2 * 3 * 3 * 3!
= 3888이다.

5턴 O로 선 X
6턴 X로 선 O (대각선 제외)
7턴 O로 선 O(대각선 제외)
7턴에서 O가 승리하는 경우
(O를 표시하는 경우의 수) * (O를 표시하는 경우의 수에서 X가 먼저 선을 만드는 경우의 수)
= 51840 – 3888
= 47952
8턴에서 X가 승리하는 경우
(승리하는 패턴 수 * 체크 표시를 선택하는 대신 지울 수 있는 패턴의 수 * 체크 표시 중 하나를 고를 경우의 수 * X를 표시할 경우의 수 * O를 표시할 경우의 수)
= 8 * 3 * 6 * 3! * 5P4
= 8 * 3 * 6 * 6 * (5*4*3*2)
= 103680
8턴에서 X가 승리하기 전에
5, 7턴에서 O가 먼저 선을 만드는 경우
5턴 O로 선 O(대각선 제외)
6턴 X로 선 X (대각선 제외)
7턴 O로 선 O(대각선 제외)
8턴 X로 선 O(대각선 제외)
8턴에서 X가 승리하기 전에
5, 7턴에서 O가 먼저 선을 만드는 경우

(X가 선을 그릴 수 있는 패턴 수 * 체크 표시를 선택하는 대신 지울 수 있는 패턴의 수 * 체크 표시 중 하나를 고를 경우의 수 * X를 표시할 경우의 수)
= (8 - 2) * 3 * 3 * 3!
= 324
8턴에서 X가 승리하기 전에
5, 7턴에서 O가 먼저 선을 만드는 경우

(O가 그릴 수 있는 패턴 수 * O를 표시할 경우의 수)
= 2 * (4! * 2(남은 X를 표시하고 남은 자리))
= 96 이다.
8턴에서 X가 승리하는 경우
(X를 표시하는 경우의 수) * (X를 표시하는 경우의 수에서 O가 먼저 선을 만드는 경우의 수)
= 103680 - (324 * 96)
= 72576
9턴에서 O가 승리하는 경우
(전체 경우의 수) - (4턴을 더 표시하는 경우) * (5번째 턴에서 게임이 끝나는 경우) - ... - (1턴을 더 표시하는 경우) * (8번째 턴에서 게임이 끝나는 경우)
= 9! - 4! * 1440 – 3! * 5328 – 2! * 47952 – 1! * 72576
= 127872이다.
9턴에서 무승부하는 경우

8가지
4가지
4가지
(무승부가 되는 가짓 수) * (O를 표시하는 경우의 수) * (X를 표시하는 경우의 수)
= (8 + 4 + 4) * 5! * 4!
= 16 * 5! * 4!
= 46080 이다.
9턴에서 O가 승리하는 경우
(8턴까지 선이 완성되지 않은 체로 O와 X를 표시하는 경우의 수) - (무승부가 되는 경우의 수)
= 127872 – 46080
= 81792
정리
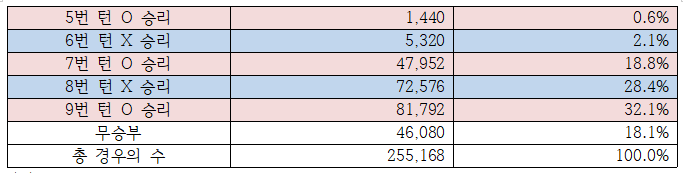
경우의 수
확률
P(O) = 0.6% + 18.8% + 32.1% = 51.5%
P(X) = 2.1% + 28.4% = 30.4%


≠
결론

https://ichef.bbci.co.uk/news/624/cpsprodpb/FE99/production/_105077156_gettyimages-124631281.jpg

https://d2vkoy1na2a6o6.cloudfront.net/images/media/screenshots/ko-kr/ss1-med-c785f55571f6c345ddaf137fa73ea0dabb39ca3f1943cdf2ef4ce9e2c027052dd743a60f5da82e8035c7ed86d2cde2c8c20888b6197abc198f7f349c5b3bd5e6.jpg
한계 및 의의
틱택토가 우리와 친근 X, 다양한 게임 X
대칭을 이용했으면 좀 더 간단하게 설명 가능

주관적인 것은 믿을 만한 것 X
불공평한 게임에 대한 보상
보고서 각주 안 넣음...
참고
경우의 수 계산이 맞는 지 확인용