1. Problema a investigar

• Introducción
• Notación
• Definición de Externalidad
• Ejemplos

• Evalúa el papel de la condicionalidad en los programas de transferencia de efectivo
• Experimento único dirigido a niñas adolescentes en Malawi.
• Dos intervenciones distintas:

​

Experimento en Malawi

Transferencia de efectivo a horgare con niñas en edad escolar

Aleatoriamente 176 (EA) -> 88 tratamiento Condicionada: asistir a la escuela (matrcicularse)

Se studia la condición y el largo plazo: formación de capital humano (ingles, matemáticas, habilidades cognitivas), matrimonio maternidad

Impacto macro y micro

• Transferencias no condicionadas (brazo UCT)  
• Transferencias condicionadas a la asistencia escolar (brazo CCT).  

II Background, Study Design, and Data

II.A Study Setting

• Malawi un país pobre y pequeño en el sur de Africa 

 II.B Sampling

• El distrito de Zomba  dividido en 550 áreas enumeradas  (EA), 250 hogares promedio
• Se eligieron 176 de diferentes extratos (ciudad, cerca rural, lejos rural), Niñas entre 13-22 nunca casadas. se dividió el grupo en dos, las que inicialmente no iban a la escuela y las que ya estaban en al escuela (baseline), para este estudio las que estaban en la escuela fueron las chida (87%)
• En cada EA (176) muestra aleatoria de las chicas que estaban inscritas en la escuela (hogares)

II.C Study Design and Intervention

• 176 (EA)  ->  88 tratamiento y 88 control
• Tratamiento (88) chicas inscritas en al escuela: (i) CCT (46) , (ii) UCT (27) de las EA (15) restantes no se hicieron ofertas a las elegibles.
• Brazo CCT. Transferencia mensual (2008 se extendió a 2009), condicionada: atender a la escuela regularmente durante, podría ser más de una chica por familia, montos familias seleccionados aleatorios ($ 4,6,8,10) y a las beneficiadas ($ 1,2,3,4,5), en el caso que aplicará colegiatura a la escuela. Mensualmente se verificaba la asistencia (80%>) y se retenía el pago en caso de no, no se removía a las no cumplidores se reanudaba si cumplían asistencia, renovaba a principio de año 

• Brazo UCT. Igual a lo anterior pero no había condición para recibir la transferencia, se ajustaba hacia arriba las transferencias para tener en promedio lo mismo que los CCT por las colegiaturas y que no fueran las cantidades a causar un sesgo

• Como resumen (después se hablara de esto) se encontrará diferencias significativas en los impactos de los programas CCT y UCT para todos los indicadores: inscripción, puntaje en exámenes, matrimonios y embarazos. Las intervenciones se percibieron diferentes una de la otra

II.D Data Sources and Outcomes

• Data sources. Se colecciono en tres rondas. Datos base o Ronda 1: antes de ofrecer el programa. Primera recopilación de datos o Ronda 2: finales 10/2008-02/2009. Segunda recopilación de datos o Ronda 3: 01-06/2010. Encuestas a las familias, datos escolares, exámenes, entrevista cualitativas (R3). (Presentan detalles de las entrevistas, duración, fechas, submuestras,etc)

• Resultados escolares. Inscripción y asistencia a la escuela con reportes personales y reportes escolares. Inscrito (1), no inscrito (0)  es una proxy débil para atención, así se utilizaron las bitácoras escolar para al atención. Se realizaron exámenes de matemáticas, lectura de inglés, comprensión de lectura, habilidades cognitivas, numero total de respuestas correctas se estandarizo para tener media 0 y varianza 1 (grupo de control), en el tratamiento se presenta como cambios en la desviación estándar (SD).  

• Resultados en matrimonio y fertilidad. ¿has estado embarazada o estas embarazada? ¿Estas casada? (R2-R3)

III. Estimation Strategy and Results

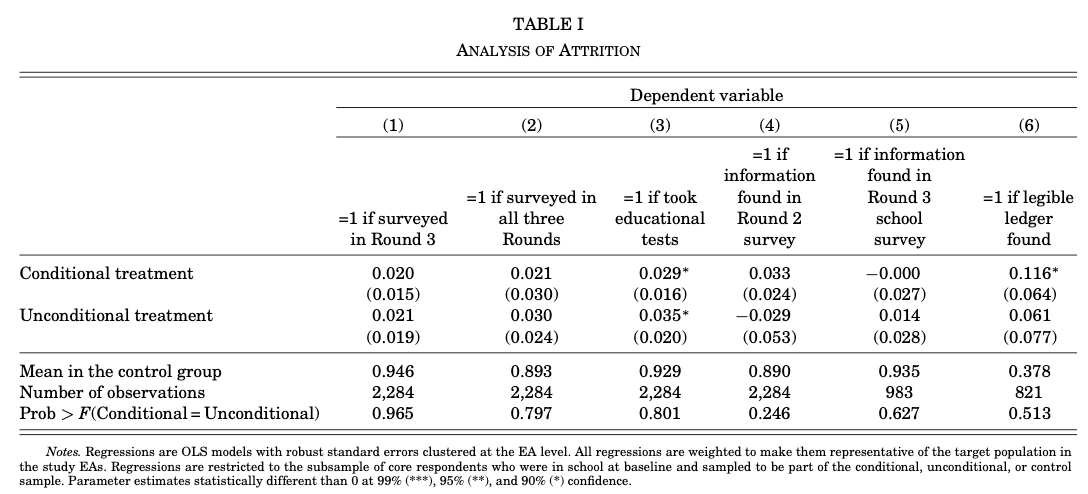
La Tabla I, resume el estudio para la atrición de la muestra. No hay atrición diferencial significativa entre los dos brazos en ninguna d ellas 6 submuestras, así el análisis de las muestras disponibles debe dar un estimador insesgado del impacto diferencial del programa.  

Atrición (desgaste). Retiro de participantes, imposibilidad de recolectar información (sesgo si hay) 

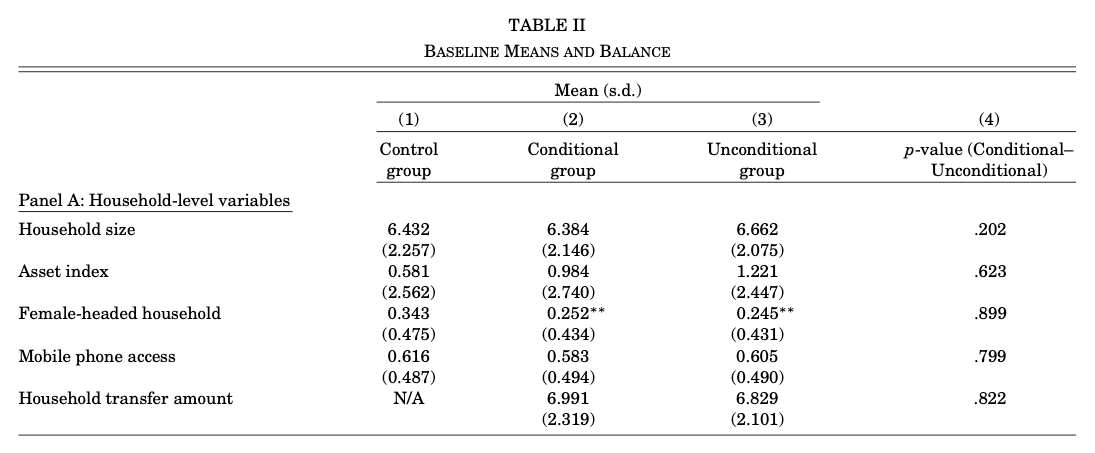
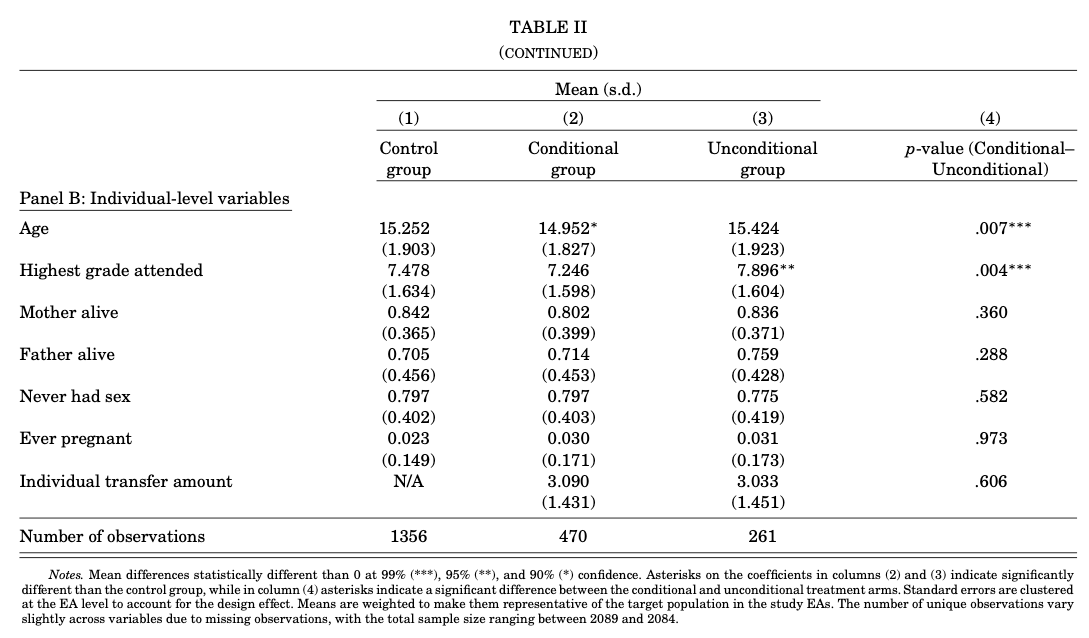
En la tabla II se muestra el balance del experimento denota que fueron exitosamente recopilados durante las tres rondas. El experimento parece bien balanceado entre el grupo de tratamiento y control.

Columna 4 muestra que solo difieren en edad y el año de inscripción, en el grupo de control es mayor

Balance. Si se observa que el experimento en verdad fue aleatorio

III.B Estimation Strategy

El estudio del diseño experimental nos da una fuente confiable de identificación.

Para estimar los efectos de la ITT (intention to tread) del programa en cada brazo de tratamiento: Inscripción, asistencia, casamientos, embarazos, se emplea el siguiente  forma:

Indicador binario

para CCT

Indicador binario

para UCT

Resultado

individuo \(i\)

Carácteristicas

Errores agrupados por EA

Variables de control: 

• Activos de Hogares
• Nivel educativo
• Inicio actividad sexual
• Edad (variable dummy) 

Se han incluido identificares por área de estratificación

III. C Results

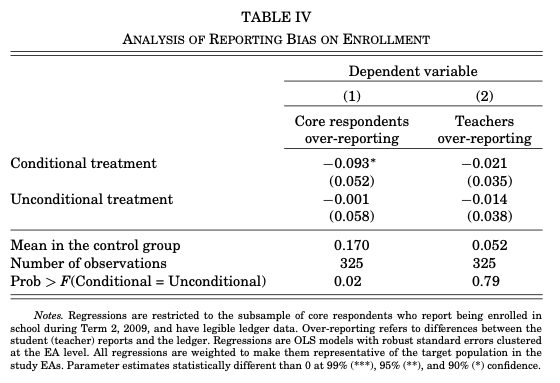
Matricula Escolar. La tabla III Tasas de matriculación por trimestre, incluye una variable acumulativa para el número de periodos que la niña estuvo matriculada durante l intervención (0-6) podría haber sesgos de notificación por los autoinformes y los monitoreos.

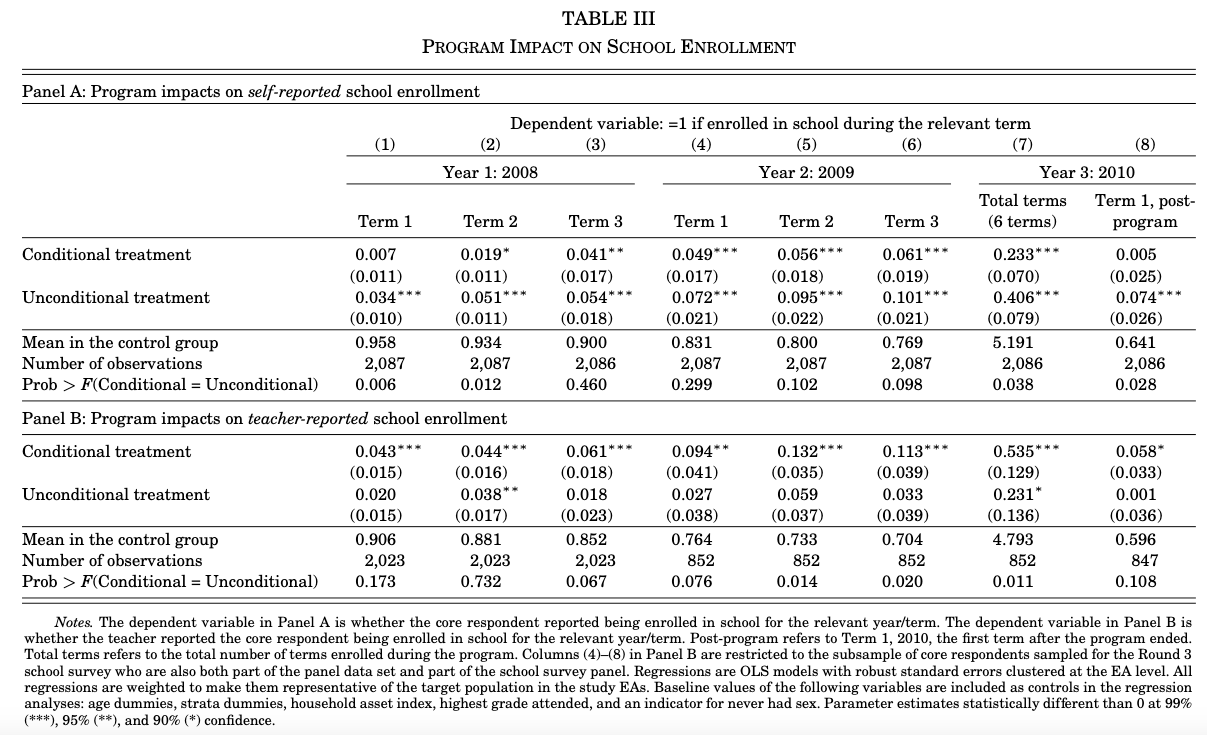
 Se tomo las diferencias de los estudiantes y profesores con las  bitácoras escolares (Term 2, 2009), 17% del grupo de control nunca asistio 

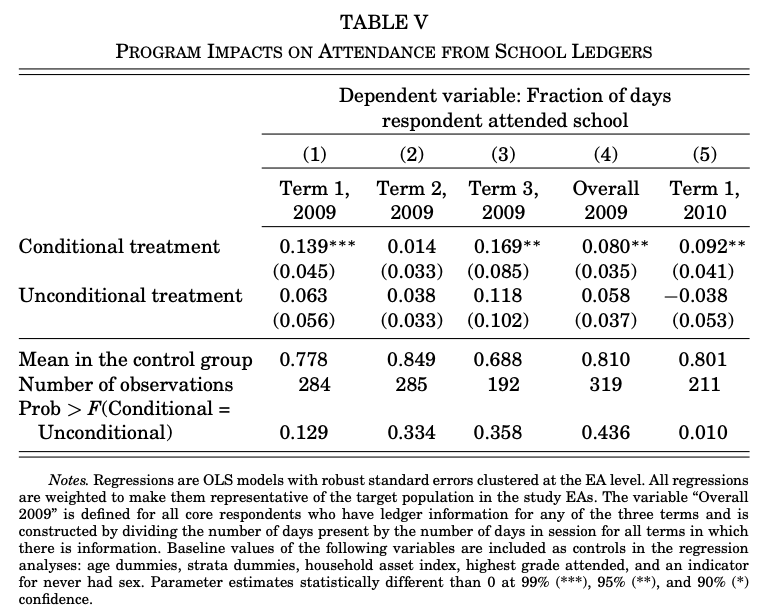
Asistencia escolar (margen intensivo). Asistencia de matriculados 2009 y el primer trimestre de 2010 (Ronda 3). Tabla V indica la asistencia en el grupo de control máxima de 85% y mínima de 69%, en el Term 1 2009 se necesita más el dinero (se mantiene altas) 

Resultados de las pruebas. 

Introducción

Nos vemos afectados por el consumo de terceros:

• vecinos que hacen ruido y estás preparando el tema de externalidades  (utilidad)
• gente que no fuma en casa y estás de invitado (consumo)
• vecino que contrata internet de banda ancha y eres webmaster (producción)

De igual forma por la producción:

• apple aumenta su producción de tablets y vendes  fundas (producción)
• Contaminación de empresas no te permite realizar actividades al aire libre (consumo)
• El vecino es sonidero y sigues preparando el tema de externalidades (utilidad)

Notación

\(X^i \subset \mathbb{R}_+^L\) conjunto de consumo para le consumidor \(i\)

\(L\) número de bienes, \(l=1,\ldots,L\)

\(I\) número de consumidores, \(i=1,\ldots,I\)

\(J\) número de firmas, \(j=1,\dots,J\)

\(x^i=(x_1^i,\ldots,x_L^i )\in X^i\), vector de consumo

\(w^i=(w_1^i,\ldots,w_L^i )\in \mathbb{R}_+^L\), vector de dotación

\(Y^j \subset \mathbb{R}^L\) conjunto de producción para la firma \(j\)

\(y^j=(y_j^i,\ldots,y_L^j )\in Y^j\), vector de producción

\(f^j\), función de producción

\(p \in \mathbb{R}_+^L\), vector de precios

\(p\cdot y^j\), beneficios de la empresa \(j\)

\(\theta^{ij}\in\mathbb{R}_+\), contribución de la firma \(j\) al consumidor \(i\)

\(R^{i}=p\cdot w^i+\sum\limits_j\theta^{ij}p\cdot y^j\), ingreso del consumidor \(i\)

Externalidad

Cualquier efecto indirecto que la actividad de producción o consumo tenga sobre la función de utilidad, el conjunto de consumo o el conjunto de producción.

Definición de Externalidad

Efecto indirecto. El efecto es creado por un agente económico  distinto al afectado (efecto externo) y tal efecto no se transmite mediante los precios (no pecuniario).

• Externalidad por consumo
• Externalidad por producción

7. Conclusiones del estudio

• Introducción
• Notación
• Definición de Externalidad
• Ejemplos

• Aunque hubo una disminución moderada en la tasa de abandono en el grupo de UCT en comparación con el grupo de control, fue solo un 43% tan grande como el impacto en el grupo de CCT al final del programa de 2 años.  
• El grupo CCT también superó al grupo UCT en las pruebas de comprensión de lectura en inglés.  Sin embargo, las tasas de embarazo y matrimonio de adolescentes fueron sustancialmente más bajas en el grupo UCT que en el grupo CCT, debido enteramente al impacto del UCTS en estos resultados entre las niñas que abandonaron la escuela. 
• Mayor asistencia en los CCT 
• Las pruebas cognitivas mejoran en el CCT las ganancias no son detectadles en el UCT
• En resumen CCT ventajas significativa en resultados escolares, inscripción y aprendizaje (modesta) sobre el UCT
• Tasas Matrimonio y embarazo predominan en UCT (44 y 27 %) menor que el control al final de dos años mientras que en el CCT fueron menores y no signifiactivas
• Cuando tienes CCT negar los veneficios a las personas que incumplen pasa por alto los vbeneficios que se pueden causar
• UCT  mejoran cosas pero menos efectivos en la condición
• ¿qué se quiere lograr?
• CCT y UCT diferentes comunidades mismo distrito

Economía particular

Existen dos externalidades:

• Externalidad por consumo \(x_1\)
• Externalidad por producción \(y_1^1\)

Las tecnologías están dadas por:

• \(y_{1}^{1}=f^{1}\left(y_{2}^{1}\right)\)
• \(y_{2}^{2}=f^{2}\left(y_{1}^{2}, y_{1}^{1}, x_{1}\right)\)

\(f^j\) diferenciable y concava

La función de utilidad es:

• \(U(x_1,x_2)\)

\(U\), diferenciable, creciente y estricatmente cuasiconcava

La dotación inicial:

• \((w_1,w_2)\)

El óptimo de Pareto para esta economía se obtiene resolviendo el siguiente problema

Sujeto a:

Donde \(\left(\lambda_{1}, \lambda_{2}, \mu_{1}, \mu_{2}\right)\) son los mutiplicadores de Kuhn-Tucker. Se asumen todas las condiciones necesarias para tener soluciones interiores (concavidad, saturación)

Se tienen las siguientes condiciones de primer orden

Pigou (1920's): se tienen que tomar en cuenta los efectos directos e indirectos de las actividades económicas

Sustituyendo una unidad del bien \(x_1\) por una unidad del bien \(x_2\), la producción del bien dos se ve afectada:

por eso su nivel de utilidad cambia (se agrega)

Por lo tanto la tasa (social) marginal de sustitución es

• \(y_{1}^{1}=f^{1}\left(y_{2}^{1}\right)\)
• \(y_{2}^{2}=f^{2}\left(y_{1}^{2}, y_{1}^{1}, x_{1}\right)\)

• \(y_{1}^{1}=f^{1}\left(y_{2}^{1}\right)\)
• \(y_{2}^{2}=f^{2}\left(y_{1}^{2}, y_{1}^{1}, x_{1}\right)\)

Puesto que la actividad de la firma 2 no crea una externalidad, su tasa (social) marginal de sustitución  es igual a su tasa privada

• \(y_{1}^{1}=f^{1}\left(y_{2}^{1}\right)\)
• \(y_{2}^{2}=f^{2}\left(y_{1}^{2}, y_{1}^{1}, x_{1}\right)\)

La firma 1 debe considerar que usando un a unidad adicional del bien 2 como entrada, produce

Consecuentemente afecta la producción del bien 2 por

de lo cual se sigue que la tasa (social) marginal de transformación esta dada por

La organización óptima de la producción no necesariamente requiere la eliminación total de las externalidades incluso si estas son negativas

Conclusión

• \(y_{1}^{1}=f^{1}\left(y_{2}^{1}\right)\)
• \(y_{2}^{2}=f^{2}\left(y_{1}^{2}, y_{1}^{1}, x_{1}\right)\)

Si consumir y producir el bien 1, afecta la producción del bien 2 negativamente. Esto no significa que el bien 1 debe dejar de ser producido en su totalidad. Más bien en la evaluación del costo social del bien 1, los costos externos deben ser internalizados