Centro de Investigación y Docencia Económicas, A.C.

Maestría en economía

Macroeconomía II

Daniel Hernández

Federico Daverio

Guillermo Woo

Rafael Martínez

Marzo 2020

Brain drain and economic growth: theory and evidence

Beine, M., Docquier, F., Rapoport, H.: Brain drain and economic growth: theory and evidence. Journal of Development Economics 64(1), 275-289 (2001). url: www.sciencedirect.com/science/article/pii/S0304387800001334

Contenido

Introducción
Modelo
Validación empírica
Conclusiones

Introducción

Se analiza el Impacto de las perspectivas de migración en la formación de capital humano y su impacto en el crecimiento de una pequeña economía abierta.

Se asume heterogeneidad de los agentes en cuanto a decisiones de formación y habilidad

Motivación

Externalidades negativas (Bhagwati and Hamada, 1974), como puede ser la sustitución imperfecta entre trabajo calificado y el que no lo es (Piketty, 1977)

Efectos positivos en la formación de capital humano, sin embargo, en el agregado se genera un detrimento al crecimiento.

Crecimiento a largo plazo

El crecimiento a largo plazo depende fundamentalmente de la acumulación de capital humano. No obstante se debe ser cauteloso respecto a los efectos de la migración:

Sin perspectivas de migración, situemos en un país pobre como Yemen, con un bajo potencial de crecimiento. En este caso al no existir condiciones que incentiven la educación, las perspectivas de crecimiento son nulas o muy bajas

Ahora consideremos el caso hipotético donde Yemen Mejora de alguna forma su régimen político y genera incentivos para migrar, en este escenario se puede generar un crecimiento de la población que busque prepararse para estudiar en el extranjero.

Actualmente se habla de los efectos positivos de las perspectivas de migración en un ambiente de incertidumbre, pensemos lo siguiente:

Modelo

Economía

SOE
En desarrollo
Traslape generacional
Dos PERIODOS

Crecimiento económico:

Es debido a la transmisión (promedio) intergeneracional de capital humano

Contexto del Problema

Sector productivo

Y_{t}=F(K_{t},H_{t})

K_t

H_t

y_{t}=\frac{Y_{t}}{H_{t}}

k_{t}=\frac{K_{t}}{H_{t}}

y_{t}=f(k_{t})

Capital

Trabajo

Producción/UET, forma intensiva

Capital / UET

Producción / UET

Produccción (RC)

UET = unidad eficiente de trabajo RC= Retornos Constantes

Comportamiento individual

Firma competitiva
La tasa de interés constante se fija en el mercado internacional
El salario se normaliza a la unidad
Inversión (tiempo) en educación del individuo \(i\) en \(t\)

invierte

no invierte

e_t^i=\overline{e}

e_t^i=0

e_t^i

h_{t+1}^{i}=\begin{cases} \left[1+a^{i}e_{t}^{i\beta}\right]h_{t} \text{ sin migración } (1-p)\\ \\ \left[1+wa^{i}e_{t}^{i\beta}\right]h_{t} \text{ con migración }(p) \end{cases}

0<\beta<1

a^{i} \backsim \text{Unif}[\underline{a}, \overline{a}]

h_{t+1}^{i}=h_{t}

h_{t+1}^i

Nivel de capital humano heredado en \(t\)
Nivel de capital humano en \(t+1\) para el individuo \(i\)

h_t

Se invierte en educación

No se invierte

en educación

Habilidad individual para aprender
Retornos a la educación si hay migración
Probabilidad de migrar

a^i

w>1

h_{t}(1-\overline{e})+ \frac{p\left[1+wa^{i}\overline{e}^{\beta}\right]h_{t}}{1+r} + \frac{(1-p)\left[1+a^{i}\overline{e}^{\beta}\right]h_{t}}{1+r} \geq h_{t}+ \frac{h_{t}}{1+r}

a_{i} \geq a_{E} \equiv \frac{\overline{e}^{1-\beta}(1+r)}{\Phi (p,w)}

\Phi (p,w) \equiv 1 + p (w-1)

Se supone un agente neutral al riesgo (Utilidad de Bernoulli es la identidad) y el interés por maximizar el valor esperado del ingreso

E\left(h_{t}(1-{e}_t^i)+ \frac{h_{t+1}^i}{1+r}\right)

Convendrá invertir en educación cuando

Despejando

\(a_E\) es la capacidad del agente crítico, el cual es indiferente a invertir o no en educación

\begin{cases} a_{F} \equiv \overline{e}^{1-\beta}(1+r); P_{F}=max\left\{0;\frac{\overline{a}-a_{F}}{\overline{a}-\underline{a}}\right\} &\text{ si \(p=0\)} \\ a_{M} \equiv \frac{\overline{e}^{1-\beta}(1+r)}{w}=\frac{a_{f}}{w}; P_{M}=0 &\text{ si \(p=1\)} \\ a_{E} \equiv \frac{\overline{e}^{1-\beta}(1+r)}{1+p(w-1)}; P_{E}=max\left\{0,\frac{(1-p)(\overline{a}-a_{E})}{a_{E}-\underline{a}+ (1-p)(\overline{a}-a_{E})}\right\}&\text{ si \(0 < p < 1\)} \end{cases}

a_{F} < a_{e} < a_{M},

\(P_{E}\) puede ser más pequeño o más grande que \(P_{F}\)

h_{t+1}=\frac{\overline{a}-\underline{a}}{a_{E}-\underline{a}+(1-p)(\overline{a}-a_{E})} \left[\int_{\underline{a}}^{a_{E}}h_{t}U(a) da + (1-p)\int^{\overline{a}}_{a_{E}}(1+a\overline{e}^\beta)h_{t}U(a) da\right]

g_{t+1}=\frac{h_{t+1}-h_{t}}{h_{t}}=\frac{(1-p)\overline{e}^{\beta}\left(\overline{a}^2-a_{E}^2\right)}{2\left[a_{E}-\underline{a}+(1-p)\left(\overline{a}-a_{E}\right)\right]}

Tomando el promedio de capital humano para heredar en la siguiente generación

Efecto cerebro

Efecto fuga

\frac{\partial g}{\partial p} < 0

\frac{\partial g}{\partial a_E} \frac{d a_E}{dp} >0

dg =\frac{\partial g}{\partial p} dp + \frac{\partial g}{\partial a_E}d a_E = \frac{\partial g}{\partial p} dp + \frac{\partial g}{\partial a_E} \frac{d a_E}{dp}dp=\left(\frac{\partial g}{\partial p}+ \frac{\partial g}{\partial a_E} \frac{d a_E}{dp}\right)dp

El crecimiento

g_{F}=\frac{\overline{e}^{\beta}(\overline{a}^2-a_{F}^2)}{2\overline{a}}\> ; \> a_{F} = \overline{e}^{1-\beta}(1+r)

Suponemos \(\underline{a}=0\)

\frac{(1-p)\overline{e}^{\beta}(\overline{a}^2-a_{E}^2)}{2a_{E}+2(1-p)(\overline{a}-a_{e})} \geq \frac{\overline{e}^{\beta}(\overline{a}^2-a_{F}^2)}{2\overline{a}}

\text{recordamos que } a_{e}=\frac{a_{f}}{1+p(w-1)}

Condiciones para un BBD

Caso benchmark (autarquia)

Condiciones BBD

p\times Z(p)=p(Ap^{2}+Bp+C)<0

A=(w-1)^2, B=(w-1)\left(\frac{\overline{a}^2-a^2_{F}}{\overline{a}a_{F}}+3-w\right) C= \frac{\overline{a}^2-a^{2}_{F}}{\overline{a}a_{f}}-2(w-1)

Analizando BBD respecto a p

A=(w-1)^2 \Rightarrow \text{siempre positiva}

p > 0

Z(1)=w\frac{(\overline{a}^2-a_{f}^2 )}{\overline{a}a_{f}}

C= \frac{\overline{a}^2-a^{2}_{F}}{\overline{a}a_{f}}-2(w-1)

Casos frontera

Siempre positivo, la migración comporta siempre un efecto negativo para el país de origen

Z(1)=w\frac{(\overline{a}^2-a_{f}^2 )}{\overline{a}a_{f}}

Z(\epsilon)\cong C

Puede ser positivo o negativo dependendo del signo de C

C= \frac{\overline{a}^2-a^{2}_{F}}{\overline{a}a_{f}}-2(w-1)

Casos intermedios

La inversión en capital humano es relativamente alta en la economia cerrada

C>0

(a_{F} \> \text{suficientemente pequeño})

\text{si} \> B>0

Brain drain prevale por cualquier p -> siempre abrir fronteras perjudica el país siendo que las personas vienen escogidas entre banda que de todos modos habría estudiado

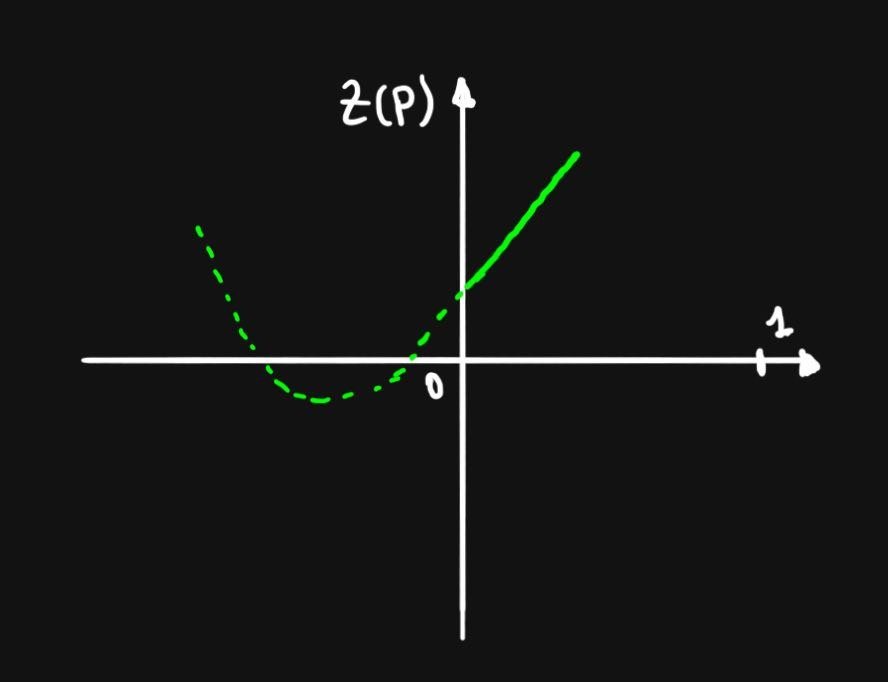
\geq \frac{\overline{e}^{\beta}(\overline{a}^2-a_{F}^2)}{2\overline{a}}

Casos intermedios

La inversión en capital humano es relativamente alta en la economia cerrada

C>0

(a_{F} \> \text{suficientemente pequeño})

\text{si} \> B<0

La probabilidad debe ser suficientemente alta para inducir un significativo brain effect pero no demasiado para no haya un fuerte drain effect

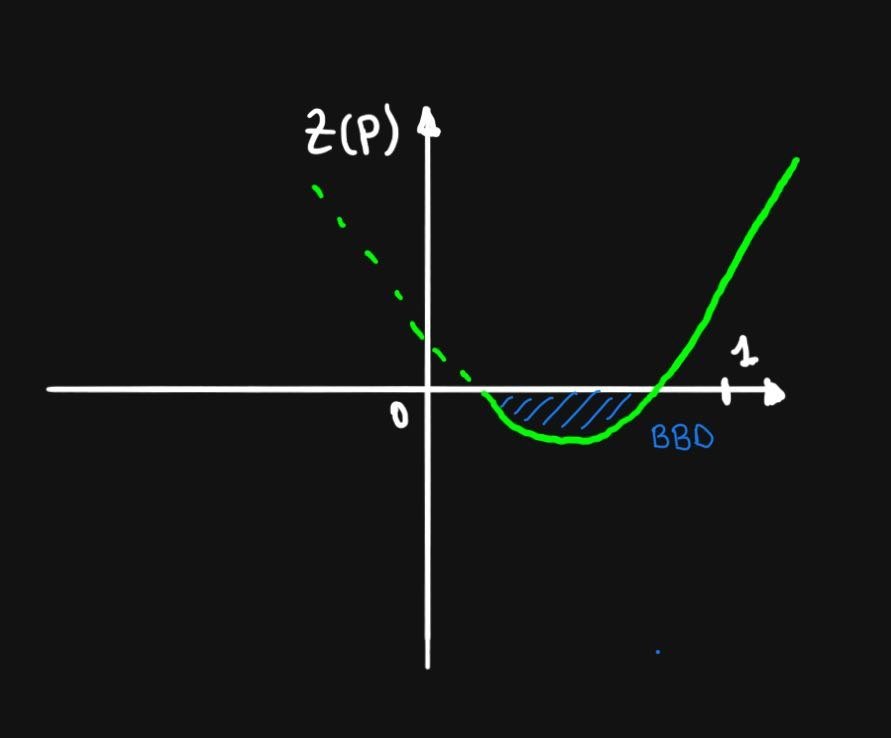
Casos intermedios

Economia en un underdevelopment trap

C<0

El prevaler de un BBD es esperada para valores no demasiados altos de la probabilidad de emigrar

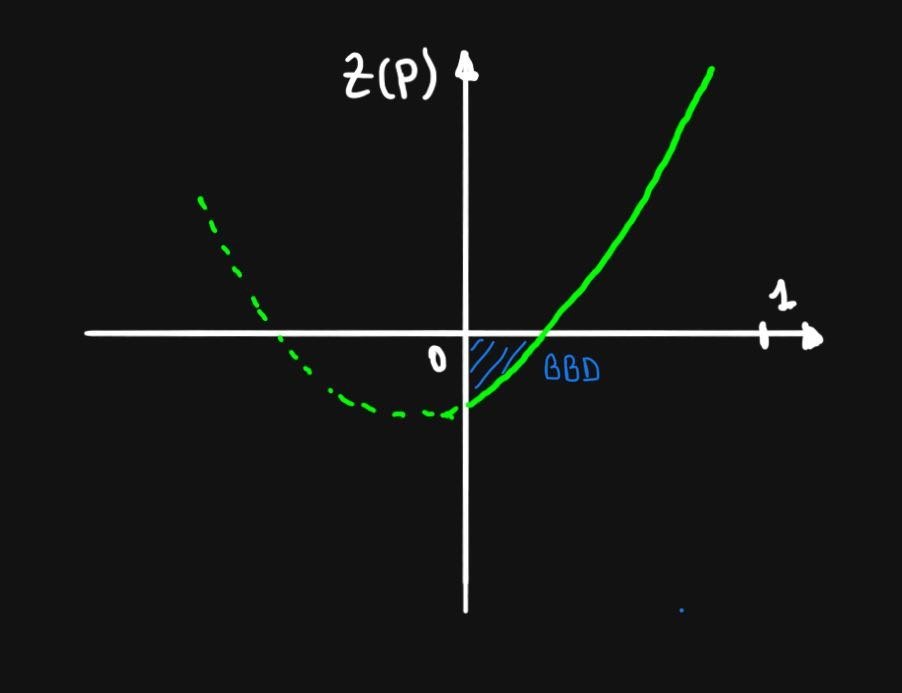
Validación Empírica

Evidencia empírica

El modelo permite comprobar tres hipótesis de manera empírica.

Relación positiva entre oportunidades de migración y la proporción de individuos que deciden invertir en educación.
Relación positiva entre tasa de crecimiento y porcentaje de población educada.
Relación negativa entre tasa de crecimiento y flujos de emigración de población educada.

Efecto cerebro

Efecto fuga

\frac{\partial g}{\partial p} < 0

\frac{\partial g}{\partial a_E} \frac{d a_E}{dp} >0

\frac{\bar{a} - a_{E}}{\bar{a} - \underline{a}} = \frac{1}{\bar{a} - \underline{a}} \left( \bar{a} - \frac{\bar{e}^{(1- \beta)}(1 + r)}{1 + p(w -1 )} \right)

Problemas con datos

No existen datos armonizados entre países de las características de habilidades y/o educación de sus inmigrantes.

Autores utilizan las tasas de migración como variable proxy de "fuga de cerebros".

Medición de flujos migratorios.
- Declaraciones de inmigración de países receptores (OCDE, 1997).
Problema de utilizar flujos de migración y no datos específicos de "fuga de cerebros".
- La ecuación podría capturar por otros efectos además del incentivo en invertir en capital humano.
- Remesas: afectan crecimiento y capital humano.

Especificación y resultados

Endogeneidad en migración \(\rightarrow\) 'Instrumentar' con una regresión para estimar migración
Relación no lineal entre acumulación de CH y probabilidades de migración \(\rightarrow\) \(plev_i = 1\) si país está en 'vías de desarrollo'

mig_i = \textbf{0.366} diff_i - \textbf{0.554} pop_i - 0.144 epub_i

hum_i = - \textbf{0.444} - 0.016 mig_i + \textbf{0.075} mig_i * plev_i + \textbf{0.161}epub_i

grw_i = - \textbf{0.050} -0.004 mig_i + \textbf{0.084} hum_i + 0.134 rem_i

Conclusiones

Primer impacto, “potencialmente benéfico” es que las oportunidades de migrar incentivan la inversión en educación “Brain Effect”.

Segundo Impacto, perjudicial es la fuga de cerebros “Drain Effect”.

El modelo se centra en el impacto de las migraciones en la formación de capital humano y en el crecimiento, a partir de ello los autores señalan.

Cautela en la imposición de barreras a la movilidad en el caso de que la educación sea financiada públicamente, pues esto puede generar efectos contrarios

Es importante generar incentivos que reconozcan el valor del capital humano, mediante subsidios y política fiscal se debe buscar retener a la población educada necesaria para mantener o generar el crecimiento.

Politicas publicas

El modelo se centra en el impacto de las migraciones en la formación de capital humano y en el crecimiento a partir de ello los autores señalan.

Subsidios a la educación resultan ineficientes cuando la probabilidad de migrar a un lugar con un mejor salario respecto al lugar de origen es alta, en este caso no es necesario subsidiar.

Comentarios finales

Hipótesis de salario exógeno \(w\)
El flujo migratorio en el país de destino deberá determinar una disminución de la productividad marginal
Esquema de producción sobre el cual no se concluye (¿ingreso del agente representativo?)
La distribución de habilidades se intuye no uniforme
No en trivial invertir en educación

Brain drain and economic growth: theory and evidence

Contenido

Introducción

Se analiza el Impacto de las perspectivas de migración en la formación de capital humano y su impacto en el crecimiento de una pequeña economía abierta.

Se asume heterogeneidad de los agentes en cuanto a decisiones de formación y habilidad

Motivación

Externalidades negativas (Bhagwati and Hamada, 1974), como puede ser la sustitución imperfecta entre trabajo calificado y el que no lo es (Piketty, 1977)

Efectos positivos en la formación de capital humano, sin embargo, en el agregado se genera un detrimento al crecimiento.

Crecimiento a largo plazo

Sin perspectivas de migración, situemos en un país pobre como Yemen, con un bajo potencial de crecimiento. En este caso al no existir condiciones que incentiven la educación, las perspectivas de crecimiento son nulas o muy bajas

Ahora consideremos el caso hipotético donde Yemen Mejora de alguna forma su régimen político y genera incentivos para migrar, en este escenario se puede generar un crecimiento de la población que busque prepararse para estudiar en el extranjero.

Modelo

Economía

Crecimiento económico:

Contexto del Problema

Sector productivo

Comportamiento individual

El crecimiento

Condiciones para un BBD

Analizando BBD respecto a p

Casos frontera

Casos intermedios

Casos intermedios

Casos intermedios

Validación Empírica

Evidencia empírica

Problemas con datos

Especificación y resultados

Conclusiones

Primer impacto, “potencialmente benéfico” es que las oportunidades de migrar incentivan la inversión en educación “Brain Effect”.

Segundo Impacto, perjudicial es la fuga de cerebros “Drain Effect”.

Cautela en la imposición de barreras a la movilidad en el caso de que la educación sea financiada públicamente, pues esto puede generar efectos contrarios

Es importante generar incentivos que reconozcan el valor del capital humano, mediante subsidios y política fiscal se debe buscar retener a la población educada necesaria para mantener o generar el crecimiento.

Politicas publicas

Subsidios a la educación resultan ineficientes cuando la probabilidad de migrar a un lugar con un mejor salario respecto al lugar de origen es alta, en este caso no es necesario subsidiar.

Comentarios finales