Interconexión de sistemas       Diferenciales LTI

 

Dr. Rafel Martínez Martínez

Abril 2018

         Respuesta en frecuencia

        de  sistemas LTI

 

Dr. Rafel Martínez Martínez

Abril 2018

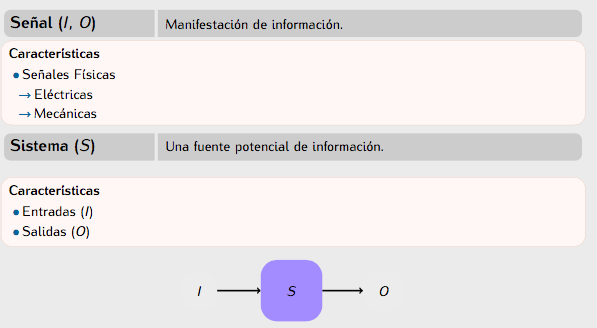
ideas y definiciones

Sistemas diferenciales

 

  • En una ecuación diferencial la salida es la solución de la ecuación

 

 

  • Las operaciones correspondientes a la entrada es a lo que se "iguala" la ecuación diferencial 
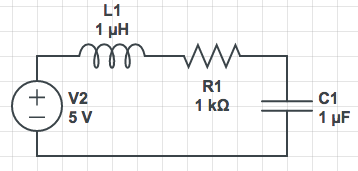
\frac{d^2}{dt^2}y(t)+\frac{R}{L}\frac{d}{dt}y(t)+\frac{1}{LC}y(t)=\frac{1}{L}\frac{d}{dt}x(t)
d2dt2y(t)+RLddty(t)+1LCy(t)=1Lddtx(t)\frac{d^2}{dt^2}y(t)+\frac{R}{L}\frac{d}{dt}y(t)+\frac{1}{LC}y(t)=\frac{1}{L}\frac{d}{dt}x(t)
\frac{d^2}{dt^2}y(t)+\frac{R}{L}\frac{d}{dt}y(t)+\frac{1}{LC}y(t)=\frac{1}{LC}x(t)
d2dt2y(t)+RLddty(t)+1LCy(t)=1LCx(t)\frac{d^2}{dt^2}y(t)+\frac{R}{L}\frac{d}{dt}y(t)+\frac{1}{LC}y(t)=\frac{1}{LC}x(t)

salida la corriente del circuito

salida el voltaje en el capacitor

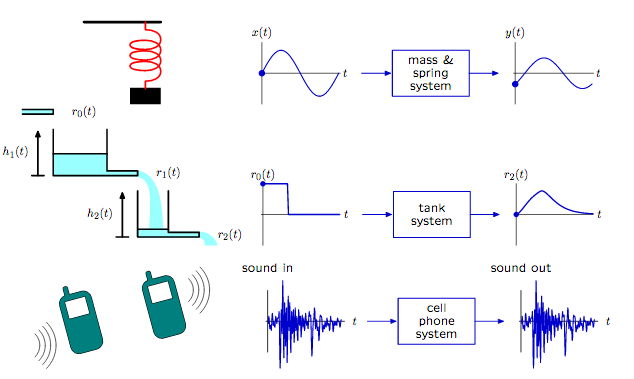
Sistemas LTI

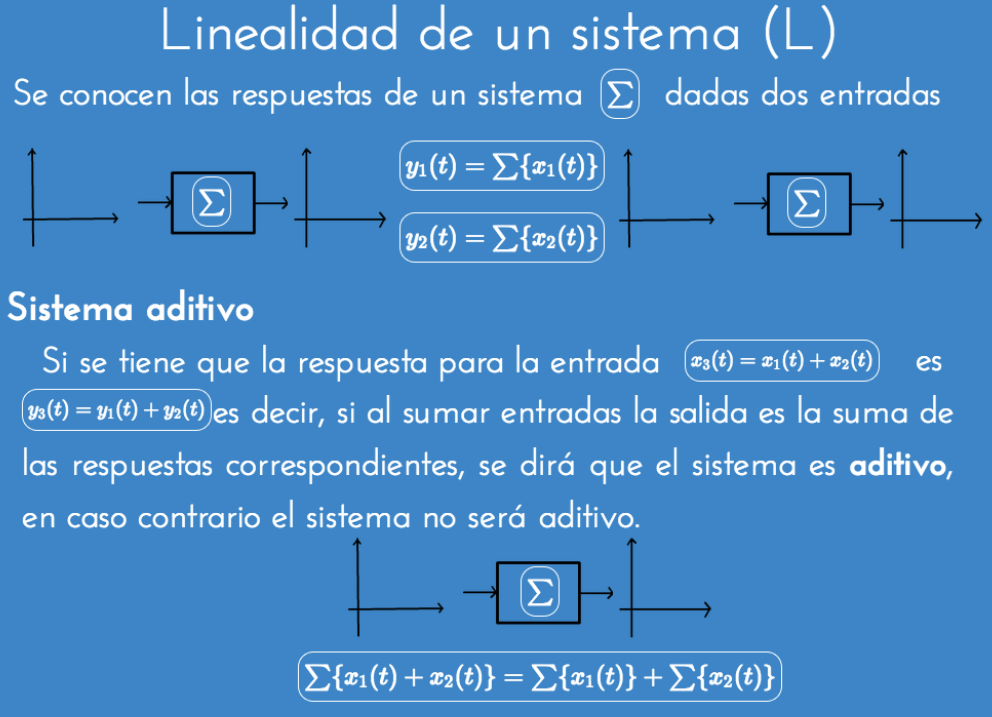
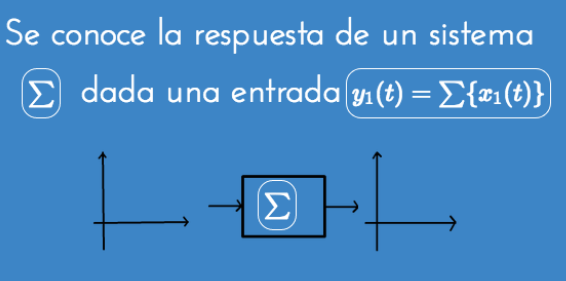
Delta de Dirac

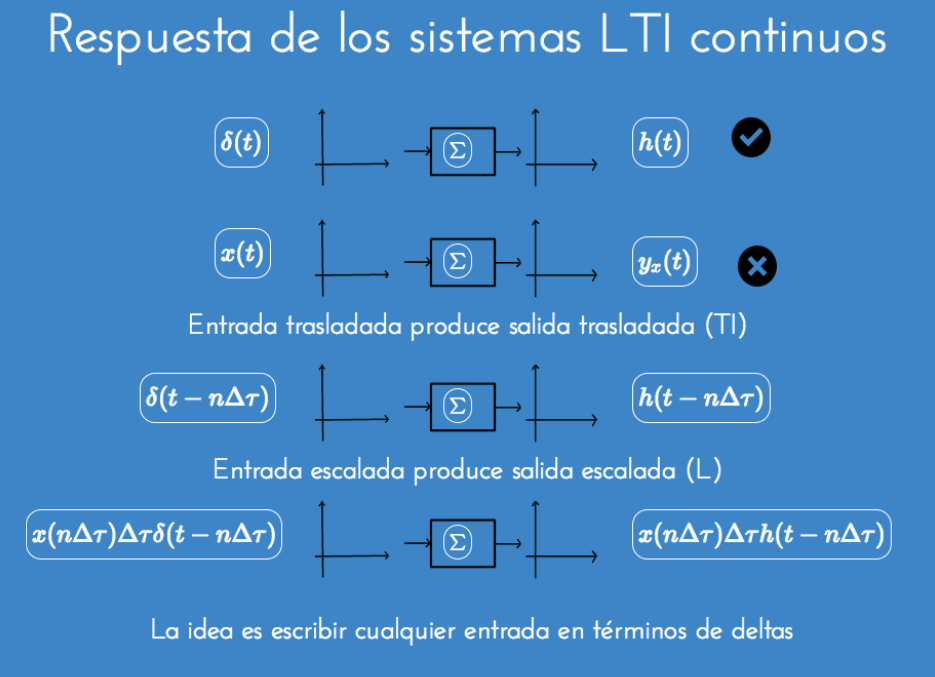
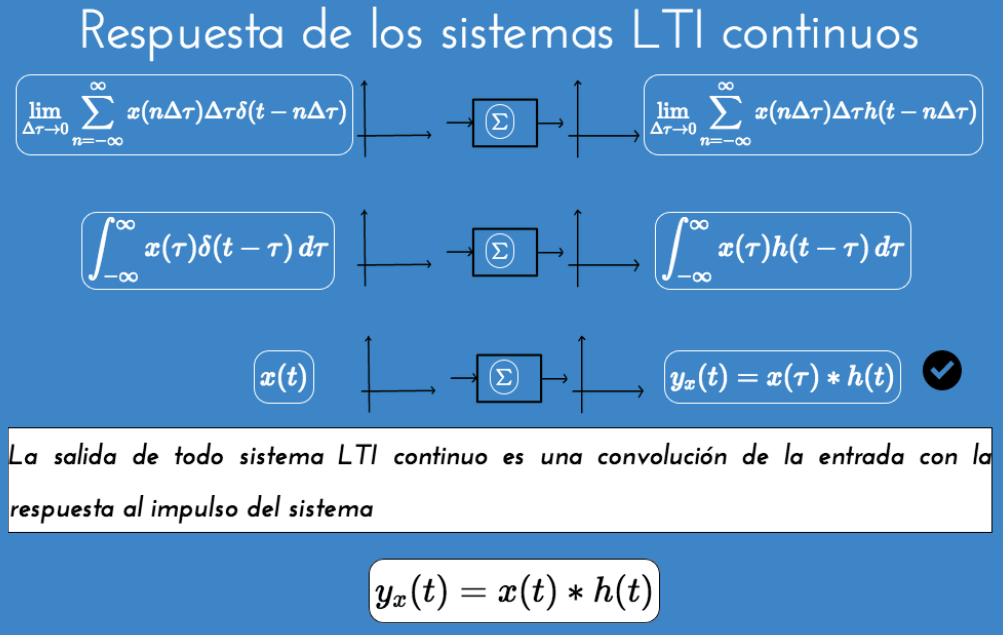
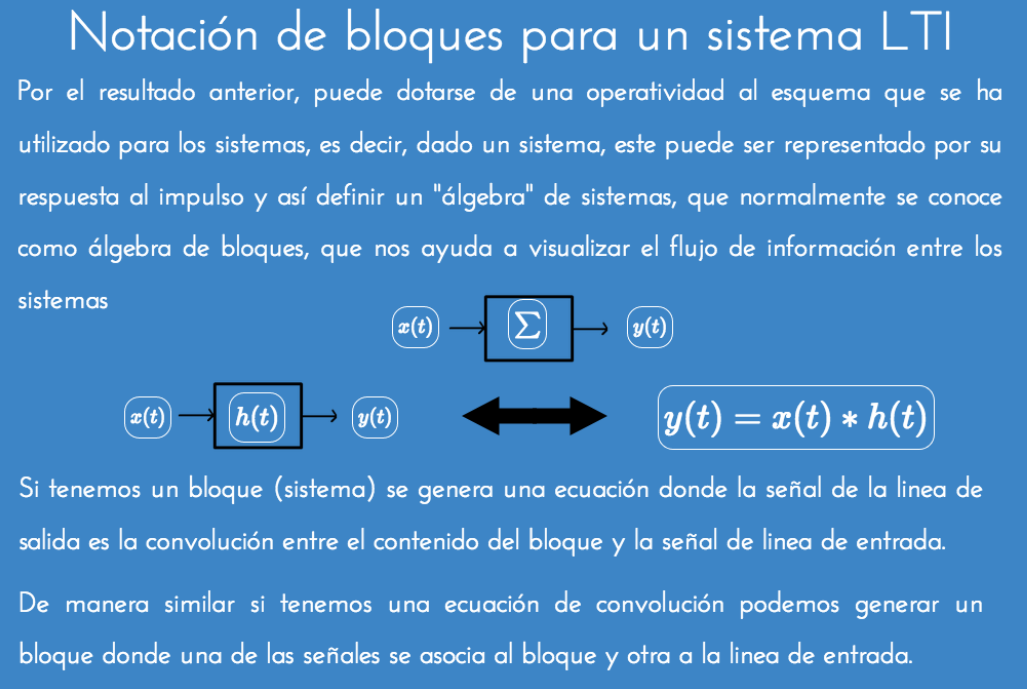
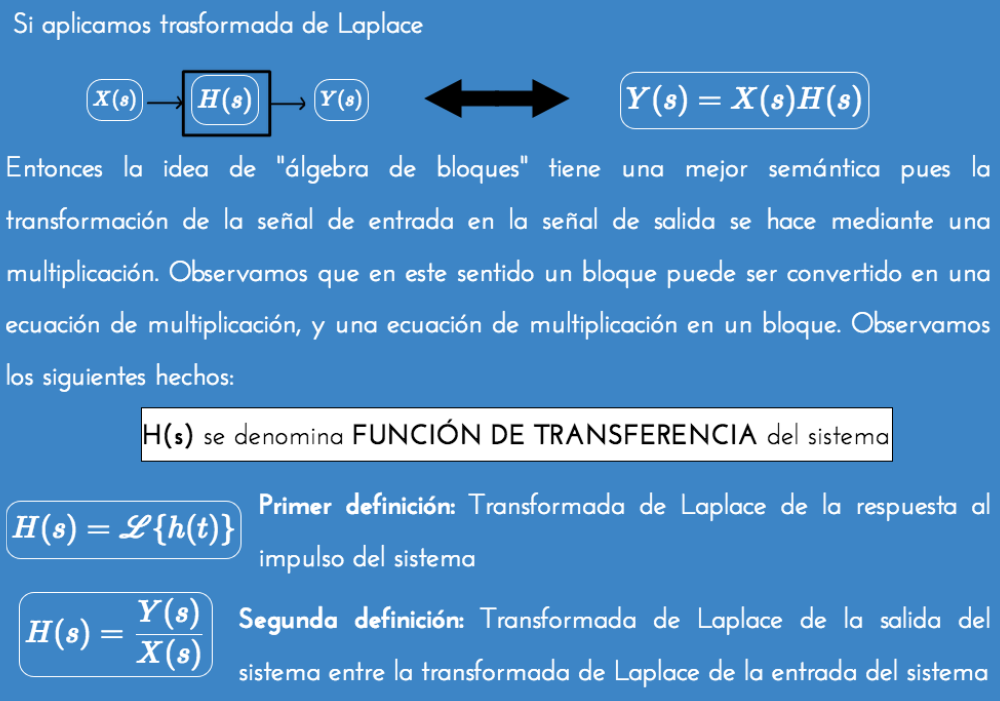
Conexión de sistemas LTI

 

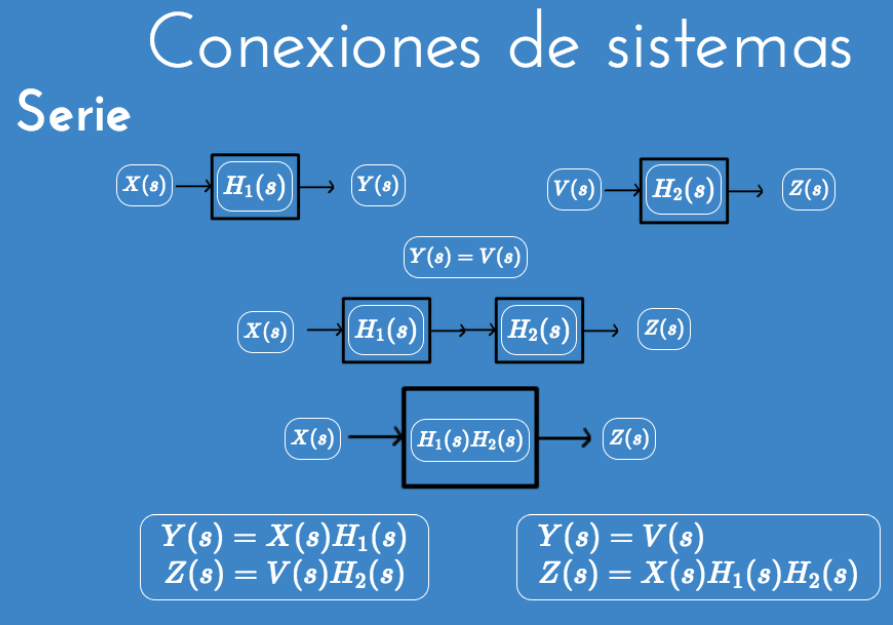
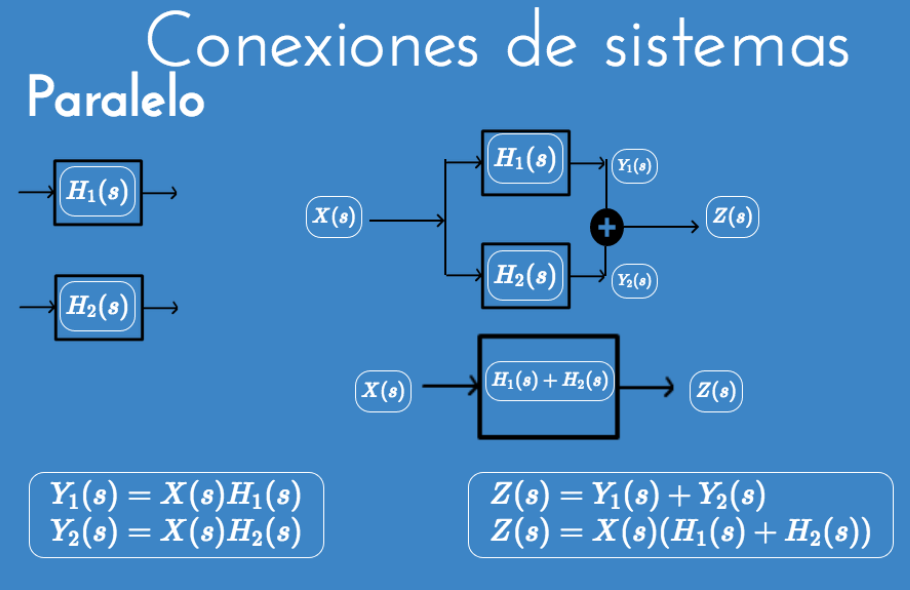
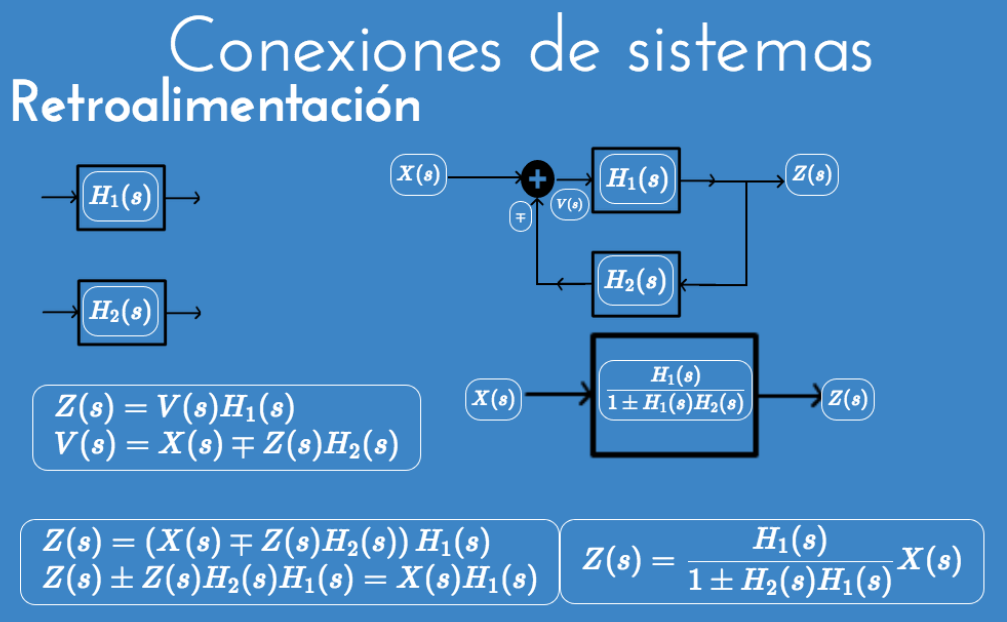
Ejemplos

 

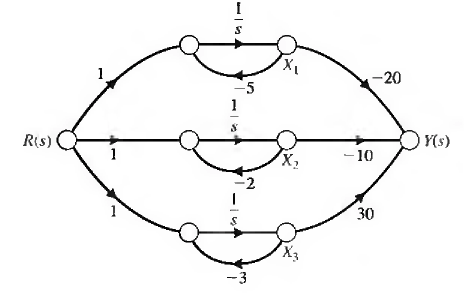
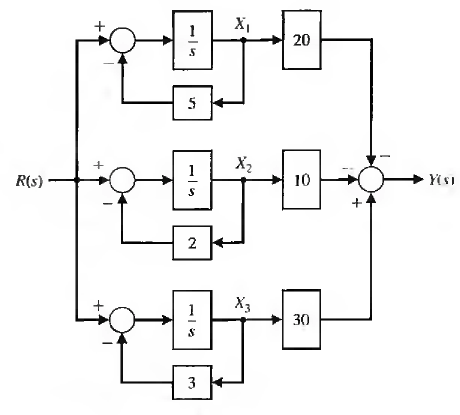
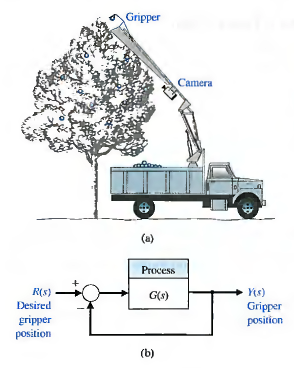
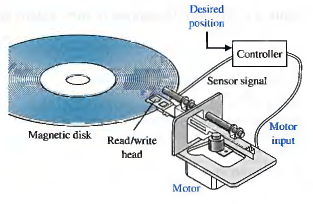
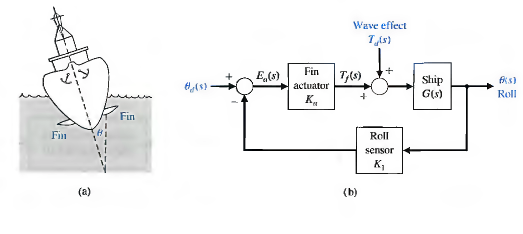
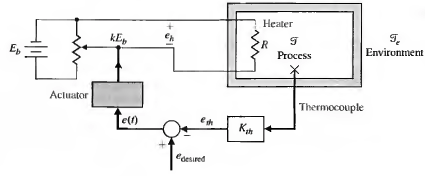
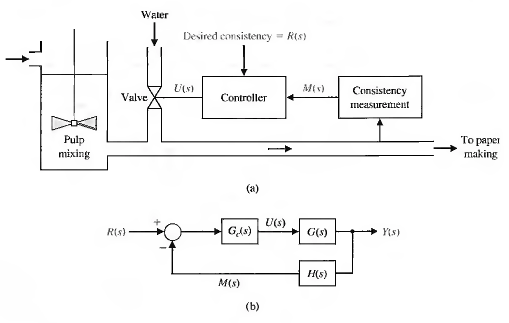
Respuesta en frecuencia de sistemas LTI

Diagramas de bode

Enlace

Made with Slides.com