Estatística

Data Science & Big Data 

Rafael Erbisti

Aula 4 - Conceitos básicos de Probabilidade e Inferência Estatística

 Introdução

  • A Teoria das Probabilidades é o ramo da Matemática que cria, desenvolve e pesquisa modelos que podem ser utilizados para estudar experimentos ou fenômenos aleatórios
  • A Inferência Estatística é totalmente fundamentada na Teoria das Probabilidades

 Experimento aleatório

Exemplos:

  1. selecionar um aluno do WIDA e observar sua idade.
  2. jogar um moeda e observar a face voltada para cima.
  3. encher um copo de água e verificar a quantidade de bactérias por cm³.
  4. selecionar pessoas na rua e perguntar se irão votar no Bolsonaro ou não.

Experimento aleatório: situação ou acontecimento cujos resultados não podem ser previstos com certeza.

Resultados possíveis (espaço amostral):

  1.  
  2.  
  3.  
  4.  
S=\{16,17,18,\ldots,90\}
S={16,17,18,…,90}S=\{16,17,18,\ldots,90\}
S=\{\textrm{cara},\textrm{coroa}\}
S={cara,coroa}S=\{\textrm{cara},\textrm{coroa}\}
S=[0,\infty)
S=[0,∞)S=[0,\infty)
S=\{\textrm{sim},\textrm{nao}\}
S={sim,nao}S=\{\textrm{sim},\textrm{nao}\}

 Alguns conceitos básicos

Axiomas de Probabilidade

  •  
  •  
  •  
P(S)=1 \textrm{ ; } P(\emptyset)=0
P(S)=1 ; P(∅)=0P(S)=1 \textrm{ ; } P(\emptyset)=0
0 \leq P(A) \leq 1
0≤P(A)≤10 \leq P(A) \leq 1
P(A \cup B) = P(A) + P(B), \textrm{ se } A\cap B= \emptyset
P(A∪B)=P(A)+P(B), se A∩B=∅P(A \cup B) = P(A) + P(B), \textrm{ se } A\cap B= \emptyset

Variável aleatória: é uma função que associa um único valor numérico a cada resultado em um espaço amostral.

Exemplo: jogar duas moedas e observar a face voltada para cima.

 

X = número de caras

 Distribuições de Probabilidade

Variáveis aleatórias discretas

  • Bernoulli
  • Binomial
  • Poisson
  • Multinomial

Variáveis aleatórias contínuas

  • Normal
  • t-student
  • log Normal
  • Gama
  • Beta
  • Uniforme

MODELOS PROBABILÍSTICOS: procuram descrever vários tipos de variáveis aleatórias - são as distribuições de probabilidade de variáveis aleatórias

 Distribuições de Probabilidade

MODELO BERNOULLI: a variável resposta X é do tipo sucesso ou fracasso.

X \sim Bernoulli(p) \hspace{0.4cm} \Longrightarrow \hspace{0.4cm} P(X=k) = p^k(1-p)^{1-k} \textrm{ , } k=0,1
X∼Bernoulli(p)⟹P(X=k)=pk(1−p)1−k , k=0,1X \sim Bernoulli(p) \hspace{0.4cm} \Longrightarrow \hspace{0.4cm} P(X=k) = p^k(1-p)^{1-k} \textrm{ , } k=0,1

 Distribuições de Probabilidade

MODELO BINOMIAL: a variável aleatória X contém o número de tentativas que resultam em sucesso.

X \sim Binomial(n,p) \hspace{0.3cm} \Longrightarrow \hspace{0.3cm} P(X=k) = {n\choose k} p^k(1-p)^{1-k} \textrm{ , } k=0,1,\ldots,n.
X∼Binomial(n,p)⟹P(X=k)=(nk)pk(1−p)1−k , k=0,1,…,n.X \sim Binomial(n,p) \hspace{0.3cm} \Longrightarrow \hspace{0.3cm} P(X=k) = {n\choose k} p^k(1-p)^{1-k} \textrm{ , } k=0,1,\ldots,n.

 Distribuições de Probabilidade

MODELO NORMAL: muito comum e o mais importante em toda a estatística. Chamado também de modelo Gaussiano.

X \sim Normal(\mu,\sigma^2) \hspace{0.3cm} \Longrightarrow \hspace{0.3cm} f(k) = \frac{1}{\sqrt{2\pi\sigma^2}}e^{\frac{-1}{2\sigma^2}(k-\mu)^2}\textrm{ , } -\infty < k < \infty.
X∼Normal(μ,σ2)⟹f(k)=12πσ2e−12σ2(k−μ)2 , −∞&lt;k&lt;∞.X \sim Normal(\mu,\sigma^2) \hspace{0.3cm} \Longrightarrow \hspace{0.3cm} f(k) = \frac{1}{\sqrt{2\pi\sigma^2}}e^{\frac{-1}{2\sigma^2}(k-\mu)^2}\textrm{ , } -\infty &lt; k &lt; \infty.

 Exemplos

Exemplo: Volume de oxigênio absorvido numa corrida de 2km em 60 homens com idade entre 20 e 30 anos.

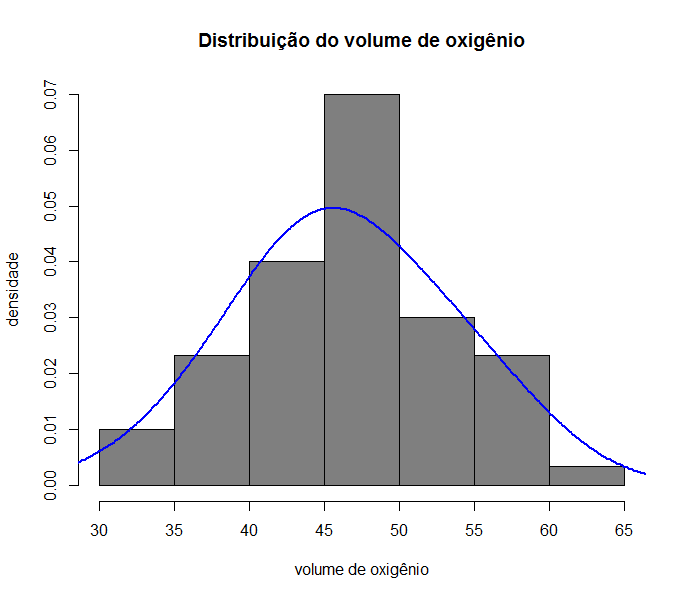
## No R

base = read.csv2(file=paste(diretorio,"oxigenio.csv",sep=""),header=TRUE)
names(base)

hist(base$volume,main="Distribuição do volume de oxigênio",ylab="densidade",
     xlab="volume de oxigênio",col="gray50",freq=FALSE)
lines(density(base$volume,adjust=2),col=4,lwd=2)

 Exemplos

Exemplo: rendimento no trabalho principal (pessoas com 14 anos +).

## No R

library(plotrix)
maximo = 10000
minimo = 0
base.new = subset(base,VD4017!="NA" & VD4017<maximo & VD4017>minimo)

par(mfrow=c(1,2),mar=c(4,4,3,0.5))
weighted.hist(base.new.teste$VD4017,w=base.new.teste$V1032,main="Distribuição da renda",
              ylab="densidade",xlab="renda no trabalho principal",col="gray50",freq=FALSE)
weighted.hist(log(base.new.teste$VD4017),w=base.new.teste$V1032,
              main="Distribuição do logaritmo \n da renda",ylab="densidade",
              xlab="logaritmo da renda no trabalho principal",col="gray50",freq=FALSE)

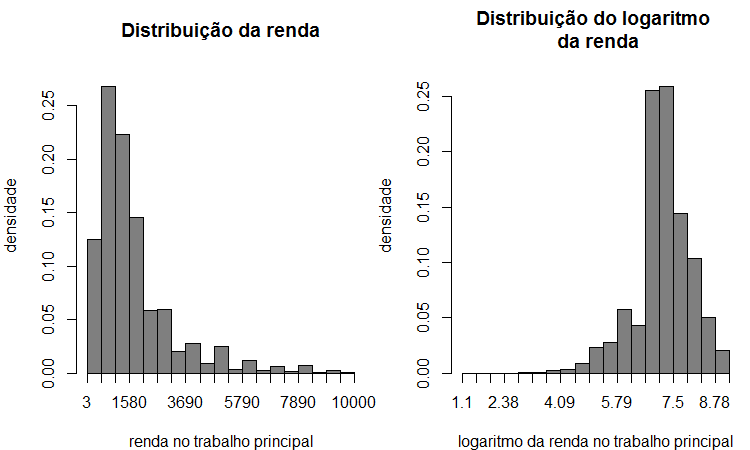
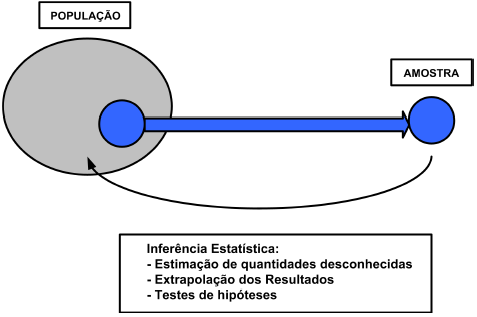
 Inferência Estatística

Inferência:  fazer afirmações sobre características de uma população, baseando-se em resultados de uma amostra

 Inferência Estatística

Intervalo de confiança:  identifica o erro cometido ao usar uma amostra para estimar um parâmetro da população.

\left[\hat \theta - \textrm{erro} ; \hat \theta + \textrm{erro}\right]
[θ^−erro;θ^+erro]\left[\hat \theta - \textrm{erro} ; \hat \theta + \textrm{erro}\right]

Fonte: Pesquisa IBOPE.

Cuidado ao interpretar um intervalo de confiança!!!

IC com nível de confiança de 95% significa que se repetirmos a pesquisa 100 vezes, em 95 delas, o IC conterá o verdadeiro valor do parâmetro populacional.

 Testes estatísticos

Teste de hipóteses: 

  1. ferramenta que permite validar (aceitar) ou refutar (rejeitar) uma alguma afirmação prévia.
  2. auxilia na decisão a ser tomada
H_0: \textrm{hipótese que queremos testar (hipótese nula)}
H0:hipoˊtese que queremos testar (hipoˊtese nula)H_0: \textrm{hipótese que queremos testar (hipótese nula)}
H_1: \textrm{hipótese alternativa}
H1:hipoˊtese alternativaH_1: \textrm{hipótese alternativa}

Hipóteses:

P-valor:

é o menor nível de significância para o qual a hipótese nula é rejeitada.

\Downarrow
⇓\Downarrow

Nível de significância:

\alpha = P(\textrm{Erro I}) = P(\textrm{Rejeitar }H_0 | H_0 \textrm{ verdadeira})
α=P(Erro I)=P(Rejeitar H0∣H0 verdadeira)\alpha = P(\textrm{Erro I}) = P(\textrm{Rejeitar }H_0 | H_0 \textrm{ verdadeira})
\textrm{Rejeita }H_0 \textrm{ se p-valor} \leq \alpha
Rejeita H0 se p-valor≤α\textrm{Rejeita }H_0 \textrm{ se p-valor} \leq \alpha

 Testes estatísticos

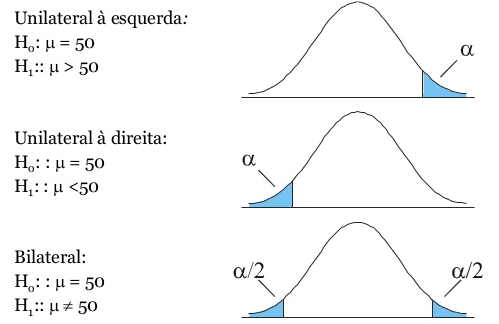
Teste de hipóteses: podem ser bilaterais ou unilaterais.

Exemplo para a média populacional

 Testes estatísticos - Exemplos

Exemplo: Verificar a quantidade de calorias num determinado produto. A empresa informa que a média de calorias de seu produto é de 30 kcal/g, mas a ANVISA afirma que é maior.

H_0: \mu = 30\\ H_1: \mu > 30\\
H0:μ=30H1:μ&gt;30H_0: \mu = 30\\ H_1: \mu &gt; 30\\
## No R:

# amostra de 25 produtos
calorias = c(30.05,29.38,28.45,31.22,31.07,34.44,34.50,34.48,31.75,30.59,
31.92,31.76,30.25,33.28,33.40,31.46,31.43,32.92,29.91,33.63,27.98,33.07,31.01,29.85,29.70)

t.test(calorias,mu=30,alternative ="greater")

        One Sample t-test

data:  calorias
t = 4.0499, df = 24, p-value = 0.0002322
alternative hypothesis: true mean is greater than 30
95 percent confidence interval:
 30.86633      Inf
sample estimates:
mean of x 
     31.5
\boldsymbol{N(\mu,\sigma^2)}
N(μ,σ2)\boldsymbol{N(\mu,\sigma^2)}

 Testes estatísticos - Exemplos

Exemplo: tianeptina é um antidepressivo. Aplicou-se a droga em dois grupos de pacientes e quantificou o nível de depressão através da escala de Montgomery-Asberg, em que os valores maiores indicam maior gravidade da depressão.

H_0: \mu_{T} = \mu_{P}\\ H_1: \mu_{T} < \mu_{P}\\
H0:μT=μPH1:μT&lt;μPH_0: \mu_{T} = \mu_{P}\\ H_1: \mu_{T} &lt; \mu_{P}\\
## No R:


placebo <- c(6,33,21,26,10,29,33,29,37,15,2,21,7,26,13,18)
tianeptina <- c(10,8,17,4,17,14,9,4,21,3,7,10,29,13,14,2)

t.test(tianeptina,placebo,alternative ="less")

     Welch Two Sample t-test

data:  tianeptina and placebo
t = -2.7788, df = 26.343, p-value = 0.004965
alternative hypothesis: true difference in means is less than 0
95 percent confidence interval:
      -Inf -3.478563
sample estimates:
mean of x mean of y 
   11.375    20.375
\boldsymbol{N(\mu,\sigma^2)}
N(μ,σ2)\boldsymbol{N(\mu,\sigma^2)}

Exemplo: renda no trabalho principal (pessoas 14 anos +) em 2017 por sexo. 

H_0: \mu_{H} = \mu_{M}\\ H_1: \mu_{H} \neq \mu_{M}\\
H0:μH=μMH1:μH≠μMH_0: \mu_{H} = \mu_{M}\\ H_1: \mu_{H} \neq \mu_{M}\\
## No R:

base <- read.csv2(file=paste(diretorio,"PNADC_2017_entr5.csv",sep=""),header=TRUE)

# Recodificando a variável Sexo
base$sexo <- NA
base$sexo[base$V2007==1] <- "Homem"
base$sexo[base$V2007==2] <- "Mulher"

base.new <- subset(base,VD4017!="NA")
base.new.h <- subset(base.new,sexo=="Homem")
base.new.m <- subset(base.new,sexo=="Mulher")

t.test(base.new.h$VD4017,base.new.m$VD4017) 

	Welch Two Sample t-test

data:  base.new.h$VD4017 and base.new.m$VD4017
t = 21.908, df = 160660, p-value < 2.2e-16
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
 327.6915 392.0856
sample estimates:
mean of x mean of y 
 2028.571  1668.683

 Testes estatísticos - Exemplos

\boldsymbol{N(\mu,\sigma^2)}
N(μ,σ2)\boldsymbol{N(\mu,\sigma^2)}

Exemplo: avaliar se proporção de crianças do sexo masculino nascidas em 2016 é de 50%.

H_0: p_{H} = 0,5\\ H_1: p_{H} \neq 0,5\\
H0:pH=0,5H1:pH≠0,5H_0: p_{H} = 0,5\\ H_1: p_{H} \neq 0,5\\
## No R:

prop.test(1435631,n=2803080,p=0.5)

    1-sample proportions test with continuity correction

data:  1435631 out of 2803080, null probability 0.5
X-squared = 1658.4, df = 1, p-value < 2.2e-16
alternative hypothesis: true p is not equal to 0.5
95 percent confidence interval:
 0.5115766 0.5127473
sample estimates:
       p 
0.512162

 Testes estatísticos - Exemplos

Segundo dados do Registro Civil (IBGE), dos  2.803.080 nascimentos 1.435.631 foram de homens

Made with Slides.com