
記憶體、位元運算與雜談
Memory, Bits & Tung^9 Sahur
臣亮言 @ NTU CSIE
April 19, 2025
Sprout 資訊之芽北區 C 班
在開始之前......
- 講師口齒不清,如果他忘記用力說話請大力提醒他
- 有任何問題都歡迎直接舉手或在 Slido 提問,不要害怕問問題
- 講師快死了,所以這次的簡報沒那麼精良,請多見諒 :(
- 因為是第二次上課所以有什麼建議也請多多指教
有一些很噁的 coding 習慣不要學- 這個投影片可以四向移動,左右切換主題,上下是同一個主題的前後
關於這堂課
- 是這學期的新規劃,所以範圍還在摸索中
- 大部分並不是程式的內容,主要是計算機概論,就算有些沒聽懂其實不太有影響
- 前一天(當天)可能六點睡,講師睡眠不足會小亢奮,不要覺得我是怪人:(
References
NTU CS1000 計算機概論
Sprout C2024-tp W8-1 變數生命週期、轉型、亂數 by 盧冠綸
Sprout C2022-tp W7-0 變數生命週期與修飾子 by 陳楷元
記憶體與位元運算
型別與轉型
生命週期
修飾子
程式與變數
位元運算
記憶體
雜談
記憶體
記憶體〉
1
進位制
這世界上有 10 種人
懂 10 進位的人跟不懂 10 進位的人
我們現在生活中的數字
通常是使用十進位制(Decimal)表示
不過實際生活中也有許多不同的進位制
像是六十進位制(時間)以及二進位制
而二進位制就是電腦使用的語言
記憶體〉
1
進位制
這世界上有 10 種人
懂 10 進位的人跟不懂 10 進位的人
重新審制一下十進位制
十進位使用的數字:0, 1, 2, 3, 4, 5, 6, 7, 8, 9
其實並沒有數字 10 吧?
所謂進位制,就是設計一套符號(0~9)
並引入進位(Carry)的概念
用這些有限的符號表示無窮的數字!
21809
個位
十位
百位
千位
萬位
我們現在生活中的數字
通常是使用十進位制(Decimal)表示
不過實際生活中也有許多不同的進位制
像是六十進位制(時間)以及二進位制
而二進位制就是電腦使用的語言
記憶體〉
1
進位制
這世界上有 10 種人
懂 10 進位的人跟不懂 10 進位的人
十進位制(Decimal)
二進位制(Binary)
2
下標
表示數字是?進位
21809
11010
重新審制一下十進位制
十進位使用的數字:0, 1, 2, 3, 4, 5, 6, 7, 8, 9
其實並沒有數字 10 吧?
所謂進位制,就是設計一套符號(0~9)
並引入進位(Carry)的概念
用這些有限的符號表示無窮的數字!
記憶體〉
1
進位制
這世界上有 10 種人
懂 10 進位的人跟不懂 10 進位的人
十進位制(Decimal)
二進位制(Binary)
2
21809
11010
對於二進位制的數字
到了\(2_{10} = 10_2\) 會進位
實際上所有進位制都是十進位
下標
表示數字是?進位
記憶體〉
1
進位制
這世界上有 10 種人
懂 10 進位的人跟不懂 10 進位的人
二進位制(Binary)
電腦(Computer)是在地化的翻譯
原文直譯稱為計算機
計算機是二進制的世界
透過許多 0, 1 計算出我們要的結果
十進位制(Decimal)
0, 1, 2, 3, 4, 5, 6, 7, 8, 9
人類世界的語言
0, 1 (F, T)
計算機世界的語言

也是為什麼描述高級工程師的畫面
會用很多 0 和 1 (???
2
21809
11010
對於二進位制的數字
到了\(2_{10} = 10_2\) 會進位
實際上所有進位制都是十進位
記憶體〉
1
進位制
這世界上有 10 種人
懂 10 進位的人跟不懂 10 進位的人
二進位制(Binary)
十進位制(Decimal)
0, 1, 2, 3, 4, 5, 6, 7, 8, 9
人類世界的語言
0, 1 (F, T)
計算機世界的語言
計算機終究是人所發明、維護的
使用二進位恐怕難以高效判讀
小試身手:
\(1010101100010111_2\)
在十進位是多少呢?
電腦(Computer)是在地化的翻譯
原文直譯稱為計算機
計算機是二進制的世界
透過許多 0, 1 計算出我們要的結果

也是為什麼描述高級工程師的畫面
會用很多 0 和 1 (???
記憶體〉
1
進位制
這世界上有 10 種人
懂 10 進位的人跟不懂 10 進位的人
二進位制(Binary)
0, 1 (F, T)
計算機世界的語言
十六進位制(Hexadecimal)
0 ~ 9, A, B, C, D, E, F
人與計算機世界共通的語言
十六進位制既能兼顧易讀性
又能簡單從二進位轉換
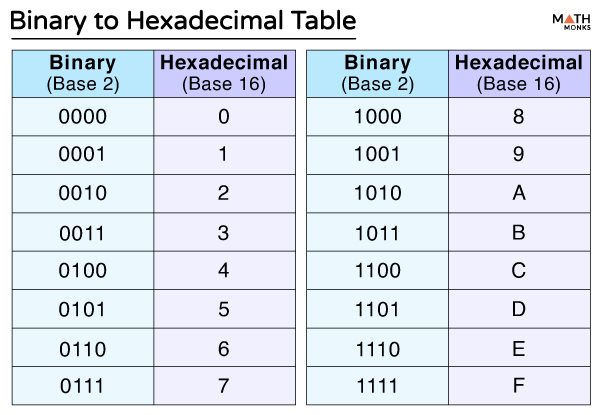
(對於十六進位也可以在前面加上\(\mathrm{0x}\)表示)
(而二進位也可以用\(\mathrm{0b}\))
2
記憶體
十進位制(Decimal)
0, 1, 2, 3, 4, 5, 6, 7, 8, 9
人類世界的語言
計算機終究是人所發明、維護的
使用二進位恐怕難以高效判讀
小試身手:
\(1010101100010111_2\)
在十進位是多少呢?
記憶體〉
1
進位制
2
記憶體
不要問我真的記憶體在幹嘛
因為我也不會
計算機是透過二進位的數字進行計算的機器
而這些數字便需要存放的地方
我們可以粗略地把存儲的地方分成硬碟與記憶體(Memory)
在買電腦、手機的時候前者就是常看到的儲存空間
硬碟和記憶體存在存取速度、造價等差異
硬碟存取慢、便宜,通常較大(256GB, 512GB, ...)
記憶體存取快、造價高、通常較小(8GB, 16GB, ...)
更重要的是記憶體的資料會在斷電後消失,而硬碟不會
所以硬碟通常用於存儲長期資料,記憶體則負責短期記憶
這世界上有 10 種人
懂 10 進位的人跟不懂 10 進位的人
二進位制(Binary)
0, 1 (F, T)
計算機世界的語言
十六進位制(Hexadecimal)
0 ~ 9, A, B, C, D, E, F
人與計算機世界共通的語言
十六進位制既能兼顧易讀性
又能簡單從二進位轉換

(對於十六進位也可以在前面加上\(\mathrm{0x}\)表示)
(而二進位也可以用\(\mathrm{0b}\))
記憶體〉
2
記憶體
不要問我真的記憶體在幹嘛
因為我也不會
八個位元稱之為一個位元組(byte)
10100010 10110111
十六進位: A2 B7一格稱為位元(bit)
每一個 Bit 有 0, 1 兩種可能性,一個 byte 也就有 \(2^8 = 256\) 種可能性
在硬體規格中常看到的 KB, MB, GB, TB 實際上就是有多少 byte
由於 \(2^{10} = 1024\approx1000\),在規格上就簡化為
K(kilo) / M(mega) / G(Giga) / T(Tera) 這類十進位數量級的形式
也就是 \(10^3/10^6/10^9/10^{12}\) bytes

計算機是透過二進位的數字進行計算的機器
而這些數字便需要存放的地方
我們可以粗略地把存儲的地方分成硬碟與記憶體(Memory)
在買電腦、手機的時候前者就是常看到的儲存空間
硬碟和記憶體存在存取速度、造價等差異
硬碟存取慢、便宜,通常較大(256GB, 512GB, ...)
記憶體存取快、造價高、通常較小(8GB, 16GB, ...)
更重要的是記憶體的資料會在斷電後消失,而硬碟不會
所以硬碟通常用於存儲長期資料,記憶體則負責短期記憶
記憶體〉
2
記憶體
3
邏輯閘
計算機建立好了數字系統,接下來就需要運算系統了
對於 0 / 1,我們習慣把他們對應到 False / True
我們便是透過一些基礎邏輯運算來構築二進位制的運算系統
可笑的是我DSDL炸了還在這裡講這個

在邏輯設計中,我們有多種基礎的邏輯閘(Logic Gate)
協助我們構築更複雜的運算系統
但畢竟這堂課不是計算機概論/數位系統與實驗/交換電路與邏輯設計
我們就簡單認識幾個有助於後續內容的邏輯閘就好
八個位元稱之為一個位元組(byte)
10100010 10110111
十六進位: A2 B7一格稱為位元(bit)
每一個 Bit 有 0, 1 兩種可能性,一個 byte 也就有 \(2^8 = 256\) 種可能性
在硬體規格中常看到的 KB, MB, GB, TB 實際上就是有多少 byte
由於 \(2^10 = 1024\approx1000\),在規格上就簡化為
K(kilo) / M(mega) / G(Giga) / T(Tera) 這類十進位數量級的形式
也就是 \(10^3/10^6/10^9/10^{12}\) bytes

不要問我真的記憶體在幹嘛
因為我也不會
記憶體〉
2
記憶體
3
邏輯閘
| 英文 | 中文 | 邏輯符號 | 邏輯意義 | 邏輯運算子 | 位元運算子 |
|---|---|---|---|---|---|
| NOT | 非 | ¬A | 反轉布林值 | ! | ~ |
| AND | 且 | A∧B | 兩者皆真,真 | && | & |
| OR | 或 | A∨B | 其一為真,真 | || | | |
| XOR | 異或 | A⊕B | 一真一假,真 | 無 | ^ |
把 0/1 對應到 False / True(假 / 真)
其實就是之前的一種變數:布林值(Boolean Value)
計算機建立好了數字系統,接下來就需要運算系統了
對於 0 / 1,我們習慣把他們對應到 False / True
我們便是透過一些基礎邏輯運算來構築二進位制的運算系統

在邏輯設計中,我們有多種基礎的邏輯閘(Logic Gate)
協助我們構築更複雜的運算系統
但畢竟這堂課不是計算機概論/數位系統與實驗/交換電路與邏輯設計
我們就簡單認識幾個有助於後續內容的邏輯閘就好
記憶體〉
2
記憶體
3
邏輯閘
| 英文 | 中文 | 邏輯符號 | 邏輯意義 | 邏輯運算子 | 位元運算子 |
|---|---|---|---|---|---|
| NOT | 非 | ¬A | 反轉布林值 | ! | ~ |
| AND | 且 | A ∧ B | 兩者皆真,真 | && | & |
| OR | 或 | A ∨ B | 其一為真,真 | || | | |
| XOR | 異或 | A ⊕ B | 一真一假,真 | 無 | ^ |
| A | B | A ∧ B |
|---|---|---|
| T | T | T |
| T | F | F |
| F | T | F |
| F | F | F |
| A | B | A ∨ B |
|---|---|---|
| T | T | T |
| T | F | T |
| F | T | T |
| F | F | F |
| A | B | A ⊕ B |
|---|---|---|
| T | T | F |
| T | F | T |
| F | T | T |
| F | F | F |
把 0/1 對應到 False / True(假 / 真)
其實就是之前的一種變數:布林值(Boolean Value)
程式與變數
CHECK POINT
| 英文 | 中文 | 邏輯符號 | 邏輯意義 | 邏輯運算子 | 位元運算子 |
|---|---|---|---|---|---|
| NOT | 非 | ¬A | 反轉布林值 | ! | ~ |
| AND | 且 | A ∧ B | 兩者皆真,真 | && | & |
| OR | 或 | A ∨ B | 其一為真,真 | || | | |
| XOR | 異或 | A ⊕ B | 一真一假,真 | 無 | ^ |
| A | B | A ∧ B |
|---|---|---|
| T | T | T |
| T | F | F |
| F | T | F |
| F | F | F |
| A | B | A ∨ B |
|---|---|---|
| T | T | T |
| T | F | T |
| F | T | T |
| F | F | F |
| A | B | A ⊕ B |
|---|---|---|
| T | T | F |
| T | F | T |
| F | T | T |
| F | F | F |
程式與變數
程式與變數〉
1
程式...?
回想一下第一堂課講的,一個 C++ 程式怎麼執行?
想法

C++ 程式碼

組合語言
(Assembly)
機器語言
(Machine Code)
endbr64
push %rbp
mov %rsp,%rbp
movl $0x1,-0x4(%rbp)
shll $0x2,-0x4(%rbp)
mov $0x0,%eax
pop %rbp
ret
f3 0f 1e fa
55
48 89 e5
c7 45 fc 01 00 00 00
c1 65 fc 02
b8 00 00 00 00
5d
c3
Coding
編譯器
(Compiler)
組譯器
(Assembler)
程式與變數〉
1
程式...?
C / C++ 是一種編譯式語言
將所有程式經過編譯器包裝後執行
在執行時,程式會向系統要求一段記憶體區段
並利用這段記憶體進行運算
其中變數就是存在這些記憶體中
Memory
記憶體是有限的
因此超出記憶體上限就會造成 MLE
而亂戳沒用到的記憶體
就會造成 Segment Fault
2
變數:整數
回想一下第一堂課講的,一個 C++ 程式怎麼執行?
想法

C++ 程式碼

組合語言
(Assembly)
機器語言
(Machine Code)
endbr64
push %rbp
mov %rsp,%rbp
movl $0x1,-0x4(%rbp)
shll $0x2,-0x4(%rbp)
mov $0x0,%eax
pop %rbp
ret
f3 0f 1e fa
55
48 89 e5
c7 45 fc 01 00 00 00
c1 65 fc 02
b8 00 00 00 00
5d
c3
Coding
編譯器
(Compiler)
組譯器
(Assembler)
Stack
Machine Code
Static Data
Heap
動態配置
(melloc, free)
一般變數
程式與變數〉
1
程式...?
2
變數:整數
10110001
一個 byte 有八個 bit,理論上能表示 \(2^8\) 種數字
\(\Rightarrow n\) 個 bits 能夠表示 \(2^n\)種數字
問題
怎麼用這些 bit 表示負數?
3
變數:浮點數
C / C++ 是一種編譯式語言
將所有程式經過編譯器包裝後執行
在執行時,程式會向系統要求一段記憶體區段
並利用這段記憶體進行運算
其中變數就是存在這些記憶體中
Stack
Machine Code
Static Data
Heap
Memory
記憶體是有限的
因此超出記憶體上限就會造成 MLE
而亂戳沒用到的記憶體
就會造成 Segment Fault
動態配置
(melloc, free)
一般變數
變數:整數
二補數(2's complement)
把最大的位數(MSB, Most Significant Bit)作為負值
1 0 1 1 0 0 0 1
\(n\) 個 bit 可以表示 \([-2^{n-1},\ 2^{n-1}-1]\)
程式與變數〉
1
程式...?
2
變數:整數
3
變數:浮點數
有些值我們保證不會是負數
就可以把所有 bit 都當作正數位來使用
這種變數型別叫做 unsigned int / long long
在修飾子會提到
10110001
一個 byte 有八個 bit,理論上能表示 \(2^8\) 種數字
\(\Rightarrow n\) 個 bits 能夠表示 \(2^n\)種數字
問題
怎麼用這些 bit 表示負數?
二補數(2's complement)
把最大的位數(MSB, Most Significant Bit)作為負值
1 0 1 1 0 0 0 1
\(n\) 個 bit 可以表示 \([-2^{n-1},\ 2^{n-1}-1]\)
- 大小:8 bytes = 64 bits
- 範圍:\([-2^{63},\ 2^{63}-1]\)
long long 長整數
- 大小:4 bytes = 32 bits
- 範圍:\([-2^{31},\ 2^{31}-1]\)
int 整數
程式與變數〉
2
變數:整數
3
變數:浮點數
在程式之中,浮點數(floating-point number)被用來紀錄小數
浮點數的名稱來自於其紀錄方式
Fixed-point
Floating-point
跟科學記號(或首尾數)非常相似
浮點數並不是紀錄一個固定的小數點
而是紀錄數值與位置與指數
- 大小:4 bytes = 32 bits
- 範圍:\([-2^{31},\ 2^{31}-1]\)
int 整數
- 大小:8 bytes = 64 bits
- 範圍:\([-2^{63},\ 2^{63}-1]\)
long long 長整數
有些值我們保證不會是負數
就可以把所有 bit 都當作正數位來使用
這種變數型別叫做 unsigned int / long long
在修飾子會提到
程式與變數〉
3
變數:浮點數
跟科學記號(或首尾數)非常相似
浮點數並不是紀錄一個固定的小數點
而是紀錄數值與位置與指數
- 4 bytes = 32 bits
- 正負:Sign bit (1-bit)
- 指數:Exponent (8-bit)
- 尾數 :Mantissa (23-bit)
float 單精度浮點數
- 8 bytes = 64 bits
- 正負:Sign bit (1-bit)
- 指數:Exponent (11-bit)
- 尾數 :Mantissa (52-bit)
double 雙精度浮點數
這裡只是極度粗淺的介紹,詳細資料可以參考 IEEE 754
在程式之中,浮點數(floating-point number)被用來紀錄小數
浮點數的名稱來自於其紀錄方式
Fixed-point
Floating-point
程式與變數〉
3
變數:浮點數
浮點數的問題是進位制換算產生的小數誤差
十進位中,10 的因數有 2 和 5
只要除數不是這兩個的倍數,就會除不盡
二進位也有這個問題
就算能在十進位中有限的小數
到了二進位也很有可能除不盡
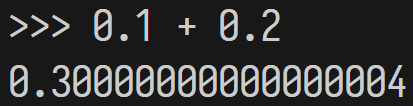
雖然剛剛用以 10 為底的科學記號舉例
但實際上數字會先被轉換為二進位制再儲存
如果數字無法在二進位中表示
就會出現浮點數誤差
因此在多數情況下非不得已不推薦使用浮點數
4
變數:布林值
- 4 bytes = 32 bits
- 正負:Sign bit (1-bit)
- 指數:Exponent (8-bit)
- 尾數 :Mantissa (23-bit)
float 單精度浮點數
- 8 bytes = 64 bits
- 正負:Sign bit (1-bit)
- 指數:Exponent (11-bit)
- 尾數 :Mantissa (52-bit)
double 雙精度浮點數
這裡只是極度粗淺的介紹,詳細資料可以參考 IEEE 754
程式與變數〉
2
變數:整數
3
變數:浮點數
4
變數:布林值
布林值理論上用一個 bit 就可以代表
但是在計算機中 byte 是操控的最小單位
所以 bool 依舊佔一個 byte
bool 布林值
- 大小: 1 byte = 8 bits
- 值:
- false = 00000000
- true = 00000001(defult)
- 0 以外的數值轉型為 bool 都會是 true
這樣很浪費空間?確實,那你可以看看 bitset
5
變數:字元
浮點數的問題是進位制換算產生的小數誤差
十進位中,10 的因數有 2 和 5
只要除數不是這兩個的倍數,就會除不盡
二進位也有這個問題
就算能在十進位中有限的小數
到了二進位也很有可能除不盡
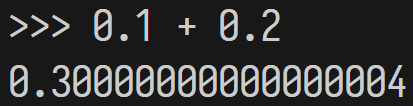
雖然剛剛用以 10 為底的科學記號舉例
但實際上數字會先被轉換為二進位制再儲存
如果數字無法在二進位中表示
就會出現浮點數誤差
因此在多數情況下非不得已不推薦使用浮點數
程式與變數〉
4
變數:布林值
5
變數:字元
char 實際上也是以整數形式存值
透過 Ascii Table 的轉換
可以把 0~127 的數值對應到表上的字元
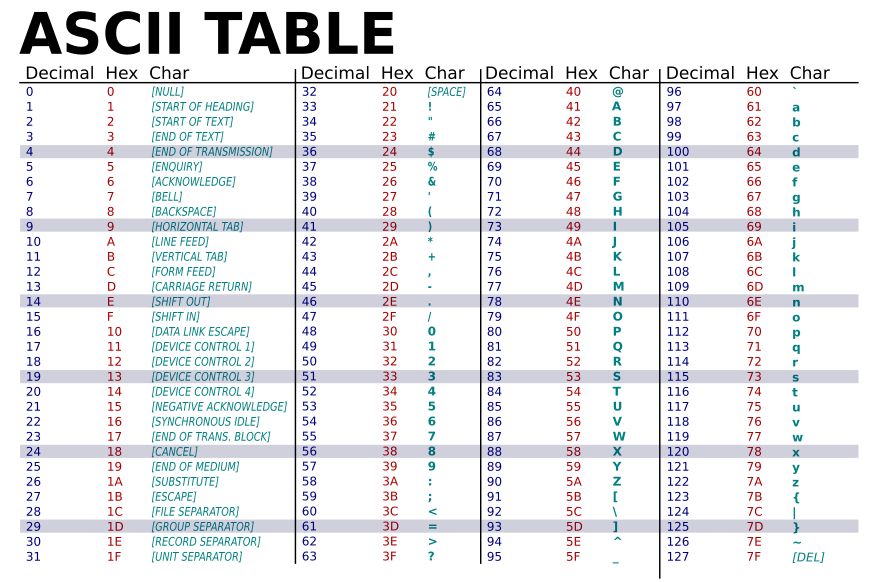
char 字元
- 大小: 1 byte = 8 bits
- 值:\([-128, 127]\)
那負數呢?
6
變數:陣列
布林值理論上用一個 bit 就可以代表
但是在計算機中 byte 是操控的最小單位
所以 bool 依舊佔一個 byte
bool 布林值
- 大小: 1 byte = 8 bits
- 值:
- false = 00000000
- true = 00000001(defult)
- 0 以外的數值轉型為 bool 都會是 true
這樣很浪費空間?確實,那你可以看看 bitset
程式與變數〉
5
變數:字元
6
變數:陣列
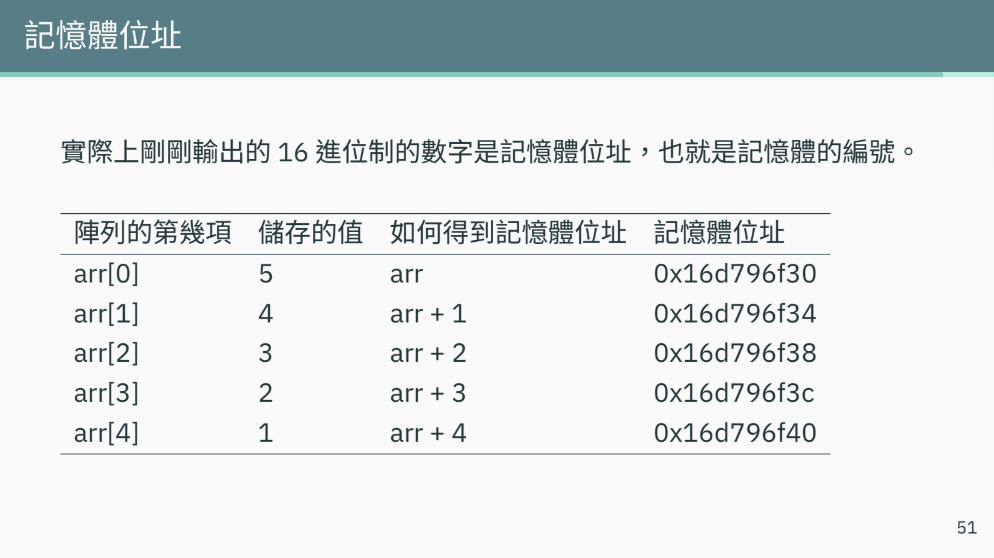
陣列(Array)實際上是一串連續記憶體
藉由索引值(index)的平移來快速存取目標值
(W4-1 一維陣列)
陣列本身是存一個記憶體位址
透過索引值平移到指定的記憶體
再讀取記憶體的值
這個其實類似指標在做的事
詳細內容二階段會提到 :D
char 實際上也是以整數形式存值
透過 Ascii Table 的轉換
可以把 0~127 的數值對應到表上的字元

char 字元
- 大小: 1 byte = 8 bits
- 值:\([-128, 127]\)
那負數呢?
位元運算
CHECK POINT
陣列(Array)實際上是一串連續記憶體
藉由索引值(index)的平移來快速存取目標值

(W4-1 一維陣列)
陣列本身是存一個記憶體位址
透過索引值平移到指定的記憶體
再讀取記憶體的值
這個其實類似指標在做的事
詳細內容二階段會提到 :D
位元運算
位元運算〉
1
Intro
剛剛提到 byte 是計算機中最小的單位
那我們怎麼對一個 bit 作操作?
| 英文 | 中文 | 邏輯符號 | 邏輯意義 | 邏輯運算子 | 位元運算子 |
|---|---|---|---|---|---|
| NOT | 非 | ¬A | 反轉布林值 | ! | ~ |
| AND | 且 | A∧B | 兩者皆真,真 | && | & |
| OR | 或 | A∨B | 其一為真,真 | || | | |
| XOR | 異或 | A⊕B | 一真一假,真 | 無 | ^ |
邏輯運算子是對變數整體操作
位元運算子則是對每一個(對)位元操作
此外,位元運算的速度比一般計算快非常多
2
NOT/AND/OR/XOR
位元運算〉
1
Intro
2
AND/OR/NOT
AND(&) 與 OR(|) 常常用來做兩件事
- 檢測指定的 bit 是 0 / 1
- 把指定的 bit 設成 0 / 1
所以在這個應用下
通常會有一個被運算的變數(被斜拋的球)
與一個拿來運算的工具變數(地球提供重力)
假設被運算的位元是 ? ,有 0, 1 兩種工具
AND/OR 一共有四種操作方式
? AND 1 -> ?:檢測該位元的值
? AND 0 -> 0:把該位元設成 0
? OR 1 -> 1:把該位元設成 1
? OR 0 -> ?:檢測該位元的值
int tester = 0b????;
int a = tester & 0b1000; //test -> ?000
int b = tester & 0b1011; // set -> ?0??
int c = tester | 0b0010; // set -> ??1?
int d = tester | 0b1110; //test -> 111?但在檢測時,AND 0才可以把其他的遮成 0
藉以讓整體的布林值直接就是該位元的結果
而 OR 1 會把其他的遮成 1,通常不是我們要的結果
剛剛提到 byte 是計算機中最小的單位
那我們怎麼對一個 bit 作操作?
| 英文 | 中文 | 邏輯符號 | 邏輯意義 | 邏輯運算子 | 位元運算子 |
|---|---|---|---|---|---|
| NOT | 非 | ¬A | 反轉布林值 | ! | ~ |
| AND | 且 | A∧B | 兩者皆真,真 | && | & |
| OR | 或 | A∨B | 其一為真,真 | || | | |
| XOR | 異或 | A⊕B | 一真一假,真 | 無 | ^ |
邏輯運算子是對變數整體操作
位元運算子則是對每一個(對)位元操作
此外,位元運算的速度比一般計算快非常多
位元運算〉
2
AND/OR/NOT
? AND 1 -> ?:檢測該位元的值
? AND 0 -> 0:把該位元設成 0
? OR 1 -> 1:把該位元設成 1
? OR 0 -> ?:檢測該位元的值
問題:
有什麼實用的地方?
1. 檢查、改寫資料存儲的結果
2. \(2^n\)的取模
\(2_{10}\) 進位 就是 \(10_2\) 進位,回想在 10 進位的時候
我們會直接看尾數來判斷 \(\mathrm{mod}\ 10^n\) 的結果
同理可以利用位元運算對尾數(\(2^n -1\)) AND 1
便能得到餘數
int test = ?;
bool odd = test & 1; // 奇數判斷
int mod8 = test & 7; // test % 8
int mod16 = test & 15; // test % 16AND(&) 與 OR(|) 常常用來做兩件事
- 檢測指定的 bit 是 0 / 1
- 把指定的 bit 設成 0 / 1
所以在這個應用下
通常會有一個被運算的變數(被斜拋的球)
與一個拿來運算的工具變數(地球提供重力)
假設被運算的位元是 ? ,有 0, 1 兩種工具
AND/OR 一共有四種操作方式
int tester = 0b????;
int a = tester & 0b1000; //test -> ?000
int b = tester & 0b1011; // set -> ?0??
int c = tester | 0b0010; // set -> ??1?
int d = tester | 0b1110; //test -> 111?但在檢測時,AND 0才可以把其他的遮成 0
藉以讓整體的布林值直接就是該位元的結果
而 OR 1 會把其他的遮成 1,通常不是我們要的結果
位元運算〉
2
AND/OR/NOT
NOT(~)是把一個變數中的所有 bit 反轉
看起來用途不大,不過通常把所有 bit 設成 0 只要 =0 就好
但當需要初始化為 1 的時候,總不可能真的打出 0b1...1 (*64)
這時候用 ~0 就可以輕鬆化解
int a = ~0; // a == -1, lol
int test = ?;
-test == ~test + 1 // True, why我們還缺一點工具 敬請期待:)
3
XOR
? AND 1 -> ?:檢測該位元的值
? AND 0 -> 0:把該位元設成 0
? OR 1 -> 1:把該位元設成 1
? OR 0 -> ?:檢測該位元的值
問題:
有什麼實用的地方?
1. 檢查、改寫資料存儲的結果
2. \(2^n\)的取模
\(2_{10}\) 進位 就是 \(10_2\) 進位,回想在 10 進位的時候
我們會直接看尾數來判斷 \(\mathrm{mod}\ 10^n\) 的結果
同理可以利用位元運算對尾數(\(2^n -1\)) AND 1
便能得到餘數
int test = ?;
bool odd = test & 1; // 奇數判斷
int mod8 = test & 7; // test % 8
int mod16 = test & 15; // test % 16位元運算〉
2
AND/OR/NOT
3
XOR
複習一下 XOR(^)的意義:「一真一假時為真」
其實中文異或給出了蠻明顯的意涵
透過 XOR 可以得到兩個變數在記憶體中相異的 bit
準確來說,兩者相同會得到 0,相異會得到 1
? ^ 0 -> ?
? ^ 1 -> ~?
Hum... 看起來不適合和 AND / OR一樣作為檢測或改寫工具
所以 XOR 的使用情景就是紀錄兩個變數相同與不同的地方
NOT(~)是把一個變數中的所有 bit 反轉
看起來用途不大,不過通常把所有 bit 設成 0 只要 =0 就好
但當需要初始化為 1 的時候,總不可能真的打出 0b1...1 (*64)
這時候用 ~0 就可以輕鬆化解
int a = ~0; // a == -1, lol
int test = ?;
-test == ~test + 1 // True, why我們還缺一點工具 敬請期待:)
位元運算〉
3
XOR
所以 XOR 的使用情景就是紀錄兩個變數相同與不同的地方
a ^= b ^= a ^= b; //swap(a, b)a':相異處為 1,相同處為 0
b:b
a':相異處為 1,相同處為 0
b':相異處是 b 的相反,相同處是 b -> a
a'':相異處是 b'(=a) 的相反,相同處是 b -> b
b':a
4
shift (<<, >>)
複習一下 XOR(^)的意義:「一真一假時為真」
其實中文異或給出了蠻明顯的意涵
透過 XOR 可以得到兩個變數在記憶體中相異的 bit
準確來說,兩者相同會得到 0,相異會得到 1
? ^ 0 -> ?
? ^ 1 -> ~?
Hum... 看起來不適合和 AND / OR一樣作為檢測或改寫工具
位元運算〉
3
XOR
4
shift (<<, >>)
你以為講完了?
還有最後一種位元運算,左移(<<)與右移(>>)
試著想想:把所有 bit 往左/右移一格,會發生什麼呢?
(不妨想想:十進位中把所有數字往左/右搬會發生什麼?)
A:左移即乘以二,右移即除以二
藉由 << / >> n,我們可以快速得到 \(\times/\div2^n\) 的結果
而且剛剛在檢查/改寫某一格 bit 的時候需要打出那個數字的二進位制
現在我們只要用 <</>> 就能動到那格的 bit!
所以 XOR 的使用情景就是紀錄兩個變數相同與不同的地方
a ^= b ^= a ^= b; //swap(a, b)a':相異處為 1,相同處為 0
b:b
a':相異處為 1,相同處為 0
b':相異處是 b 的相反,相同處是 b -> a
a'':相異處是 b'(=a) 的相反,相同處是 b -> b
b':a
位元運算〉
3
XOR
4
shift (<<, >>)
你以為講完了?
而且剛剛在檢查/改寫某一格 bit 的時候需要打出那個數字的二進位制
現在我們只要用 <</>> 就能動到那格的 bit!
int min_int = 1 << 31; // 100...00
int max_int = ~(1<<31); // 011...11
cout << min_int << " < int < " << max_int <<'\n';
int test = ?;
int bits[32] = {};
int j = 0;
for(int i = 1; i != 0; i <<= 1){
if(test & i) bits[j] = 1;
else bits[j] = 0;
j++;
}
for(int i = 31; i >= 0; i--) cout << bits[i];還有最後一種位元運算,左移(<<)與右移(>>)
試著想想:把所有 bit 往左/右移一格,會發生什麼呢?
(不妨想想:十進位中把所有數字往左/右搬會發生什麼?)
A:左移即乘二,右移即除二
藉由 << / >> n,我們可以快速得到 \(\times/\div2^n\) 的結果
位元運算〉
3
XOR
4
shift (<<, >>)
你以為講完了?
移動以後,超出上限的自然會不見
那空出來的那格要補什麼?
- <<
- 乘以二,顯然補 0
- >>
- signed:補 MSB 以維持正負性
- unsigned:補 0
而且剛剛在檢查/改寫某一格 bit 的時候需要打出那個數字的二進位制
現在我們只要用 <</>> 就能動到那格的 bit!
int min_int = 1 << 31; // 100...00
int max_int = ~(1<<31); // 011...11
cout << min_int << " < int < " << max_int <<'\n';
int test = ?;
int bits[32] = {};
int j = 0;
for(int i = 1; i != 0; i <<= 1){
if(test & i) bits[j] = 1;
else bits[j] = 0;
j++;
}
for(int i = 31; i >= 0; i--) cout << bits[i];型別與轉型
CHECK POINT
你以為講完了?
移動以後,超出上限的自然會不見
那空出來的那格要補什麼?
- <<
- 乘以二,顯然補 0
- >>
- signed:補 MSB 以維持正負性
- unsigned:補 0
型別與轉型
型別與轉型〉
1
型別?
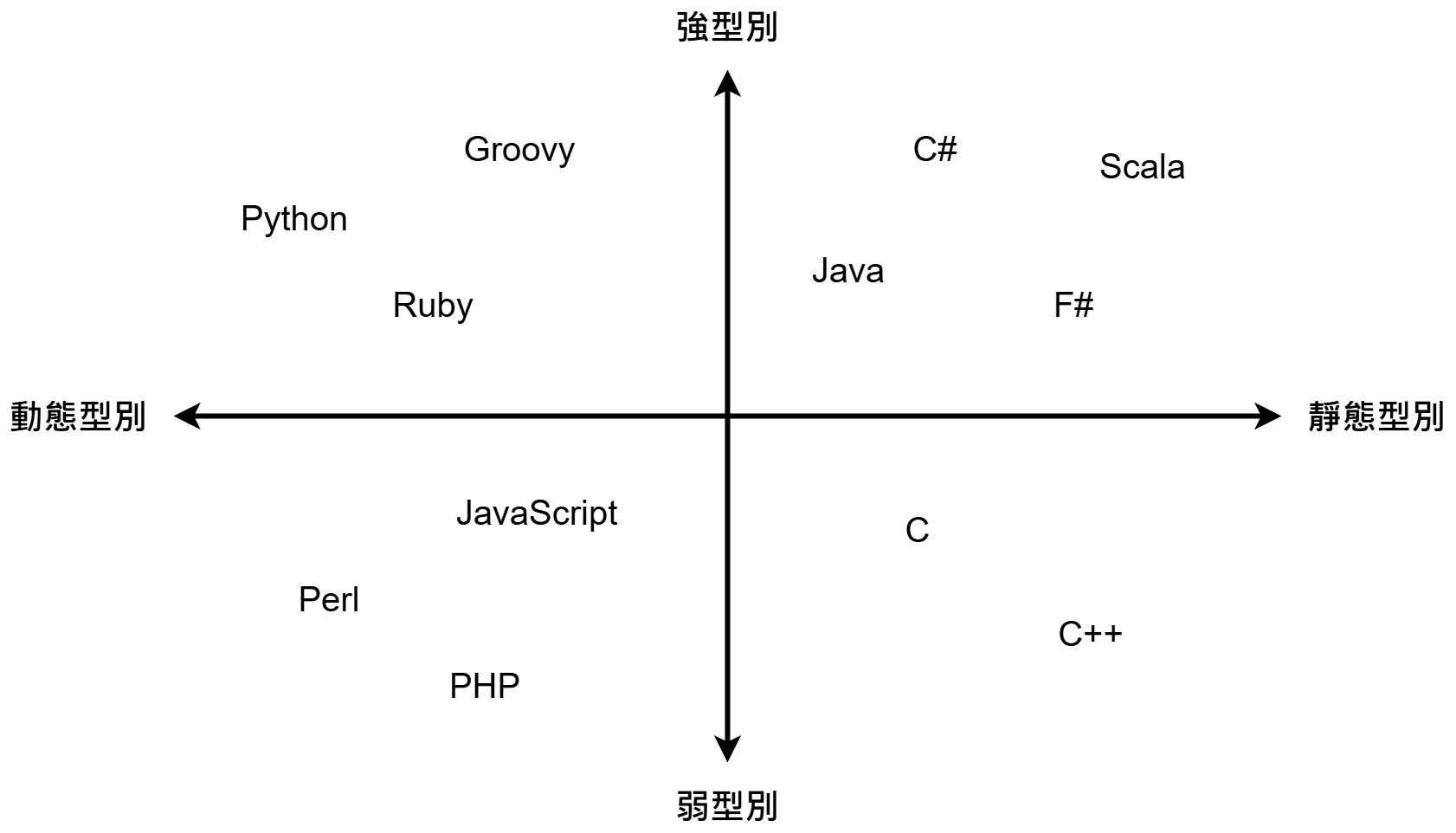
強 / 弱型別
不同型別之間是否支援混合運算
靜 / 動態型別
變數宣告時綁定型別與否
其實沒有很明確的標準
當科普看看就好
2
顯性轉型
型別與轉型〉
1
型別?
2
顯性轉型
在 C / C++ 中有分成顯性 / 隱性轉型
顯性轉型就是在程式中由我們主動協助轉型
for(int i = 0; i < 128; i++){
cout << i << ':' << (char) i << '\n';
}在欲轉換的值前面加上 (目標型別) 就能轉換型別
當然編譯器會阻止你做太過分的轉換((int)"Hello")
轉換的方向很重要,如果目標型別可以涵蓋原始型別(子集合)通常不會出錯
但若是互不隸屬(相割)就有機會出現資料失真甚至錯誤

強 / 弱型別
不同型別之間是否支援混合運算
靜 / 動態型別
變數宣告時綁定型別與否
其實沒有很明確的標準
當科普看看就好
型別與轉型〉
2
顯性轉型
在欲轉換的值前面加上 (目標型別) 就能轉換型別
當然編譯器會阻止你做太過分的轉換((int)"Hello")
轉換的方向很重要,如果目標型別可以涵蓋原始型別(子集合)通常不會出錯
但若是互不隸屬(相割)就有機會出現資料失真甚至錯誤
double a = (double)10; //10, yeah
int b = (int) 3.14; //3, simplify
int c = (int) "Hello"; //Compile Error
short d = (unsigned short)65533; //wrong
float e = 1e100; //(=1*10^100) inf3
隱性轉型
在 C / C++ 中有分成顯性 / 隱性轉型
顯性轉型就是在程式中由我們主動協助轉型
for(int i = 0; i < 128; i++){
cout << i << ':' << (char) i << '\n';
}型別與轉型〉
2
顯性轉型
3
隱性轉型
有時候一些不同型別的值一起運算時
如果有很直觀的(或是乍看合法的)運算方法
通常編譯器會自動幫我們完成型別轉換,即隱性轉型
double a = 3.5;
int b = 5;
cout << a / b;編譯器會轉成最能保持資料完整性的型別
像是除法預設是整數除法(取商)
但只要被除數 / 除數有任一個值是浮點數
就會執行浮點數的除法
在欲轉換的值前面加上 (目標型別) 就能轉換型別
當然編譯器會阻止你做太過分的轉換((int)"Hello")
轉換的方向很重要,如果目標型別可以涵蓋原始型別(子集合)通常不會出錯
但若是互不隸屬(相割)就有機會出現資料失真甚至錯誤
double a = (double)10; //10, yeah
int b = (int) 3.14; //3, simplify
int c = (int) "Hello"; //Compile Error
short d = (unsigned short)65533; //wrong
float e = 1e100; //(=1*10^100) inf型別與轉型〉
2
顯性轉型
3
隱性轉型
編譯器會轉成最能保持資料完整性的型別
像是除法預設是整數除法(取商)
但只要被除數 / 除數有任一個值是浮點數
就會執行浮點數的除法
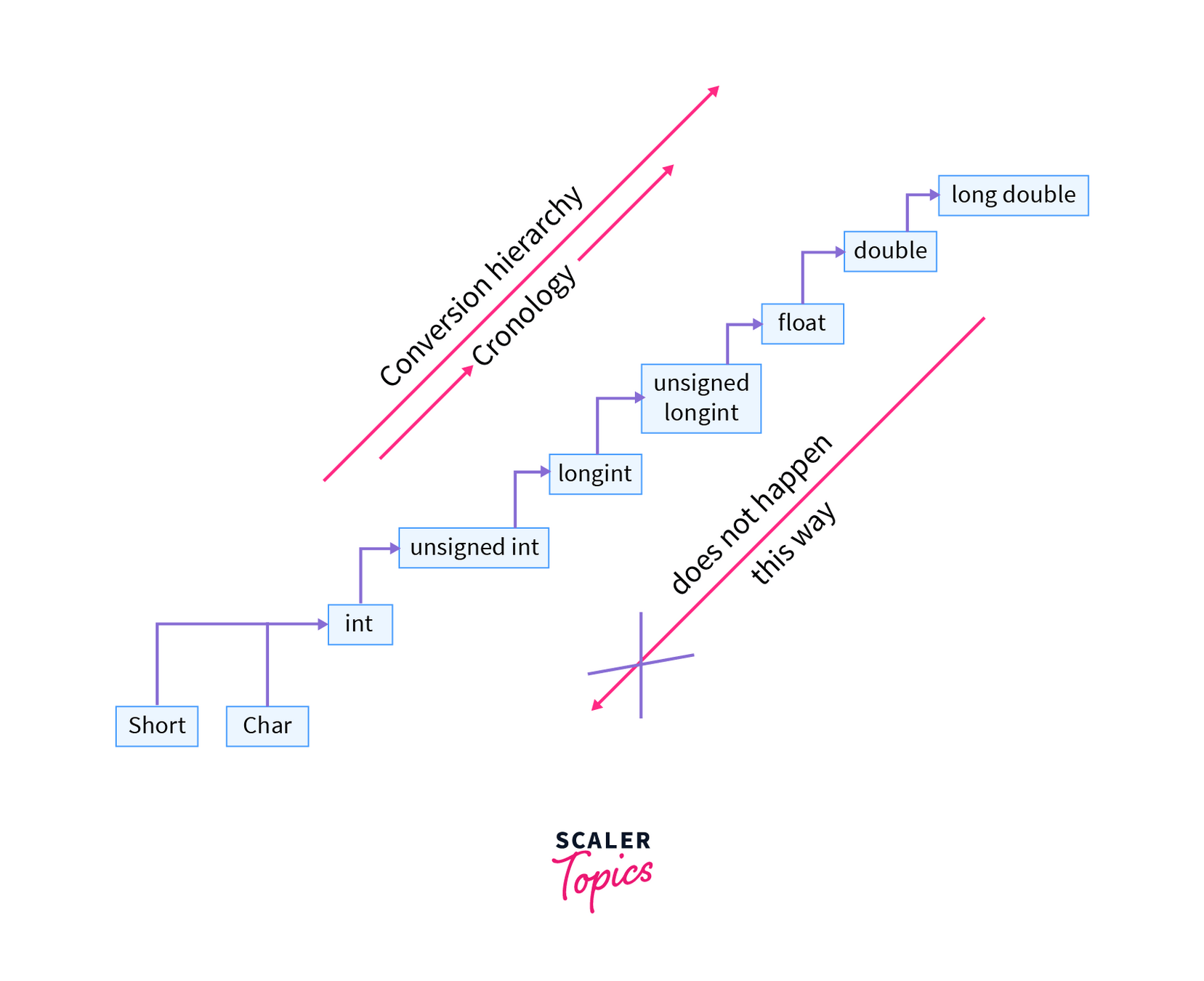
因此,整數和浮點數運算時會轉型成浮點數
範圍小的和大的整數運算會轉型成大的
(un)signed 會被轉成 unsigned
有時候一些不同型別的值一起運算時
如果有很直觀的(或是乍看合法的)運算方法
通常編譯器會自動幫我們完成型別轉換,即隱性轉型
double a = 3.5;
int b = 5;
cout << a / b;編譯器會轉成最能保持資料完整性的型別
像是除法預設是整數除法(取商)
但只要被除數 / 除數有任一個值是浮點數
就會執行浮點數的除法
型別與轉型〉
2
顯性轉型
3
隱性轉型
隱性轉型即使方便,但在一些合法但有病的操作下
編譯器(想想你 RE / SIG 幾次你覺得他有多聰明)也可能會往錯的方向解讀
然後大家都會很難過 :/
char *a = "123";
int b = a + 1; //b == 1431658501有趣的是這個 g++ 編不過,gcc 給過

編譯器會轉成最能保持資料完整性的型別
像是除法預設是整數除法(取商)
但只要被除數 / 除數有任一個值是浮點數
就會執行浮點數的除法

因此,整數和浮點數運算時會轉型成浮點數
範圍小的和大的整數運算會轉型成大的
(un)signed 會被轉成 unsigned
生命週期
CHECK POINT
隱性轉型即使方便,但在一些合法但有病的操作下
編譯器(想想你 RE / SIG 幾次你覺得他有多聰明)也可能會往錯的方向解讀
然後大家都會很難過 :/
char *a = "123";
int b = a + 1; //b == 1431658501有趣的是這個 g++ 編不過,gcc 給過

生命週期
生命週期〉
1
Scope
你是否有問過類似的問題
#include <iostream>
using namespace std;
int main(){
int tmp;
for(int i = 1; true; i++){
cin >> tmp;
if(tmp < 0){
int negative_index = i;
break;
}
}
cout << negative_index << '\n';
}
老師老師,為什麼這樣執行不了啊
生命週期〉
1
Scope
你是否有問過類似的問題
#include <iostream>
using namespace std;
int main(){
int tmp;
for(int i = 1; true; i++){
cin >> tmp;
if(tmp < 0){
int negative_index = i;
break;
}
}
cout << negative_index << '\n';
}
老師老師,為什麼這樣執行不了啊
變數如朝露,生於區塊,亡於逝括。
週而復始,不求留名,唯求一用。
所有變數都有其生命週期
也就是作用域(Scope)
通常是他所屬的那層大括號內
生命週期〉
1
Scope
你是否有問過類似的問題
#include <iostream>
using namespace std;
int main(){
int tmp;
for(int i = 1; true; i++){
cin >> tmp;
if(tmp < 0){
int negative_index = i;
break;
}
}
cout << negative_index << '\n';
}所有變數都有其生命週期
也就是作用域(Scope)
通常是他所屬的那層大括號內
變數的生命始於宣告,終於 Scope 的終止
一旦離開自己的 Scope 就不能再被存取
tmp
i
neg...
這些就是所謂的區域變數

老師老師,為什麼這樣執行不了啊
變數如朝露,生於區塊,亡於逝括。
週而復始,不求留名,唯求一用。
生命週期〉
1
Scope
#include <iostream>
using namespace std;
double average(){
return (double)sum / n;
}
int main(){
int n, sum = 0;
cin >> n;
for(int i = 0; i < n; i++){
int tmp;
cin >> tmp;
sum += tmp;
}
cout << average();
}同理也適用於函式
函式中的變數與主函式的變數不能互相參照
也就是為什麼會需要設定好傳入值
另外,函式傳入值的方式更像是另外建立一套分身
而函數內對變數的改動只會動到分身
本體依舊留在 main 函式而不受影響
因此若要透過函式改動值
除了用回傳值賦予外,只能與用指標或參數
2
重複宣告
你是否有問過類似的問題
#include <iostream>
using namespace std;
int main(){
int tmp;
for(int i = 1; true; i++){
cin >> tmp;
if(tmp < 0){
int negative_index = i;
break;
}
}
cout << negative_index << '\n';
}所有變數都有其生命週期
也就是作用域(Scope)
通常是他所屬的那層大括號內
變數的生命始於宣告,終於 Scope 的終止
一旦離開自己的 Scope 就不能再被存取
tmp
i
neg...
這些就是所謂的區域變數
生命週期〉
1
Scope
2
重複宣告
那如果在不同層 Scope 內重複宣告變數呢?
#include <iostream>
using namespace std;
int main(){
int i = 0;
if(i == 0){
int i = 1;
if(i == 1){
int i = 2;
cout << i << '\n';
}
cout << i << '\n';
}
cout << i << '\n';
}2
1
0
重複宣告的變數會再其 Scope 內
暫時覆蓋原本的變數
在這個 Scope 中改值不會影響到外層的值
等到 Scope 結束後會重新導向原先的變數
就像蓋被子一樣堆上去
等上層拿掉以後下層的還在
看起來很方便,但可讀性極低
不推薦刻意利用這個語法
#include <iostream>
using namespace std;
double average(){
return (double)sum / n;
}
int main(){
int n, sum = 0;
cin >> n;
for(int i = 0; i < n; i++){
int tmp;
cin >> tmp;
sum += tmp;
}
cout << average();
}同理也適用於函式
函式中的變數與主函式的變數不能互相參照
也就是為什麼會需要設定好傳入值
另外,函式傳入值的方式更像是另外建立一套分身
而函數內對變數的改動只會動到分身
本體依舊留在 main 函式而不受影響
因此若要透過函式改動值
除了用回傳值賦予外,只能與用指標或參數
生命週期〉
2
重複宣告
3
全域變數
有人講過了ㄏㄏ 其實這整段都有人講過了(?
有時候我們希望部分變數可以在所有函式中皆可見
同時又不想要傳來傳去
這時候可以在所有函式外宣告全域變數(global variable)
這時他的 Scope 便是整個程式的開始與終結
聽起來很棒,但是是個不好的習慣
當程式量體大起來,如果一直用全域變數
出問題會很難在一堆都直接用到這個變數的地方找到 Bug
所以使用區域變數對於維護一個大專案來說更好
大哉問:函式是不是一種全域變數
那如果在不同層 Scope 內重複宣告變數呢?
#include <iostream>
using namespace std;
int main(){
int i = 0;
if(i == 0){
int i = 1;
if(i == 1){
int i = 2;
cout << i << '\n';
}
cout << i << '\n';
}
cout << i << '\n';
}2
1
0
重複宣告的變數會再其 Scope 內
暫時覆蓋原本的變數
在這個 Scope 中改值不會影響到外層的值
等到 Scope 結束後會重新導向原先的變數
就像蓋被子一樣堆上去
等上層拿掉以後下層的還在
看起來很方便,但可讀性極低
不推薦刻意利用這個語法
修飾子
CHECK POINT
你知道現在是 4:49 嗎
有人講過了ㄏㄏ 其實這整段都有人講過了(?
有時候我們希望部分變數可以在所有函式中皆可見
同時又不想要傳來傳去
這時候可以在所有函式外宣告全域變數(global variable)
這時他的 Scope 便是整個程式的開始與終結
聽起來很棒,但是是個不好的習慣
當程式量體大起來,如果一直用全域變數
出問題會很難在一堆都直接用到這個變數的地方找到 Bug
所以使用區域變數對於維護一個大專案來說更好
大哉問:函式是不是一種全域變數
修飾子
修飾子〉
1
修飾子
在變數宣告時,我們可以加入幾個修飾子
來讓這個變數更符合我們的目的
| 修飾子 | 目的 |
|---|---|
| short / long / long long | 改變資料上下限 |
| signed/ unsigned | 有 / 無號數 |
| const | 常數 |
| static | 改變生命週期 |
2
short / long / long long
修飾子〉
1
修飾子
2
short / long / long long
其實你們都很熟 long long 了(?
long long 實際上是 long long int 的縮寫
是把 int 從 4-byte 擴展到 8-byte 的修飾詞
| 變數型態 | 佔用空間 |
|---|---|
| short (int) | 2 bytes |
| int | 4 bytes |
| long (int) | 8 bytes, at least 4 bytes |
| long long (int) | 8 bytes |
long int 並不保證是 4 or 8 bytes
雖然所有變數都爆開 long long 很爽
但 long long 也更佔空間、需要更長的運算時間
因此在對的變數選擇對的長度是一個好的習慣:D
3
signed / unsigned
在變數宣告時,我們可以加入幾個修飾子
來讓這個變數更符合我們的目的
| 修飾子 | 目的 |
|---|---|
| short / long / long long | 改變資料上下限 |
| signed/ unsigned | 有 / 無號數 |
| const | 常數 |
| static | 改變生命週期 |
修飾子〉
2
short / long / long long
3
signed / unsigned
正負數其實是看他的 sign
因此用 signed / unsigned 來區分整數與非負整數
前面我們用 2's complement 表示負數
而對於非負整數只要像一般二進位制的計法就可以了
就可以把原先拿來表示負數的數字組合用作正數
可以拓展一倍的數值範圍
| 變數型態 | 佔用空間 | 數值範圍 |
|---|---|---|
| (signed) int | 4 bytes | |
| unsigned int | 4 bytes |
其實你們都很熟 long long 了(?
long long 實際上是 long long int 的縮寫
是把 int 從 4-byte 擴展到 8-byte 的修飾詞
| 變數型態 | 佔用空間 |
|---|---|
| short (int) | 2 bytes |
| int | 4 bytes |
| long (int) | 8 bytes, at least 4 bytes |
| long long (int) | 8 bytes |
long int 並不保證是 4 or 8 bytes
雖然所有變數都爆開 long long 很爽
但 long long 也更佔空間、需要更長的運算時間
因此在對的變數選擇對的長度是一個好的習慣:D
修飾子〉
3
signed / unsigned
4
const
const 是 constant 的縮寫,也就是常數
對於一個 const 存取之後就不能改動了
如果是一個經常使用且不會變動的值就會利用 const 存取
除了防止誤動值,某些情況下也能增加程式處裡的速度
最常見的用法是題目要求對某數取模輸出
(e.g. const long long MOD = 1e9+7)
5
static
正負數其實是看他的 sign
因此用 signed / unsigned 來區分整數與非負整數
前面我們用 2's complement 表示負數
而對於非負整數只要像一般二進位制的計法就可以了
就可以把原先拿來表示負數的數字組合用作正數
可以拓展一倍的數值範圍
| 變數型態 | 佔用空間 | 數值範圍 |
|---|---|---|
| (signed) int | 4 bytes | |
| unsigned int | 4 bytes |
修飾子〉
3
signed / unsigned
4
const
5
static
static 可以幫忙改變變數的生命週期至整個程式同時不改變其 Scope
#include <iostream>
using namespace std;
void cnt(){
static int a = 0;
cout << a << '\n'
a++;
}
int main(){
cnt(); // 0
cnt(); // 1
cnt(); // 2
}好難懂...?
精準的解釋
static 變數會在編譯時就預留空間
類似於全域變數,會到程式結束才釋放記憶體
等到第一次執行宣告後實體化
之後再次跑到宣告式就不會執行了
而這個變數雖不能在函式外儲存
卻也能在離開後保留上一次執行完的值
const 是 constant 的縮寫,也就是常數
對於一個 const 存取之後就不能改動了
如果是一個經常使用且不會變動的值就會利用 const 存取
除了防止誤動值,某些情況下也能增加程式處裡的速度
最常見的用法是題目要求對某數取模輸出
(e.g. const long long MOD = 1e9+7)
修飾子〉
3
signed / unsigned
4
const
5
static
static 可以幫忙改變變數的生命週期至整個程式同時不改變其 Scope
#include <iostream>
using namespace std;
void cnt(){
static int a = 0;
cout << a << '\n'
a++;
}
int main(){
cnt(); // 0
cnt(); // 1
cnt(); // 2
}好難懂...?
粗暴的解釋
只有第一次宣告才會賦值
並且值不會消失的變數
精準的解釋
static 變數會在編譯時就預留空間
類似於全域變數,會到程式結束才釋放記憶體
等到第一次執行宣告後實體化
之後再次跑到宣告式就不會執行了
而這個變數雖不能在函式外儲存
卻也能在離開後保留上一次執行完的值