Raíra Marotta
Estatística
Curso Big Data e Data Science
Aula 7 - Introdução a Inferência Estatística
Inferência Estatística
Inferência: fazer afirmações sobre características de uma população, baseando-se em resultados de uma amostra
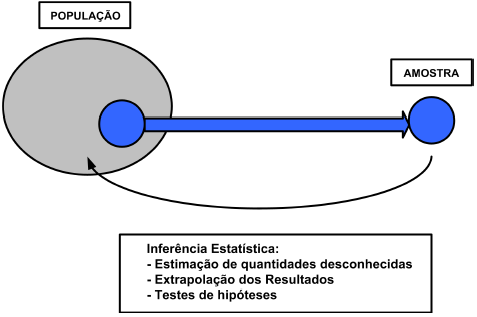
Amostragem

Se repetirmos um evento diversas vezes, poderemos obter um resultado diferente por vez. Como podemos inferir sobre a população baseado em uma amostra?
Intervalo de Confiança
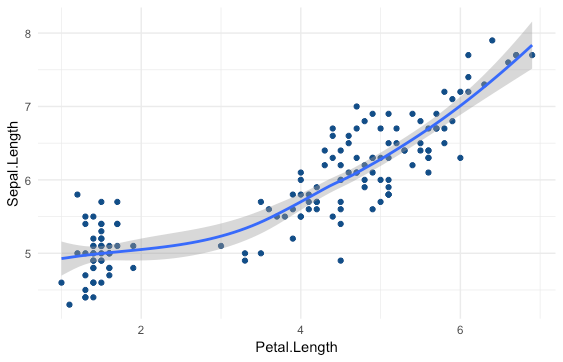
Intervalo de Confiança
Intervalo de confiança: identifica o erro cometido ao usar uma amostra para estimar um parâmetro da população.

Fonte: Pesquisa IBOPE.

Cuidado ao interpretar um intervalo de confiança!!!
IC com nível de confiança de 95% significa que se repetirmos a pesquisa 100 vezes, em 95 delas, o IC conterá o verdadeiro valor do parâmetro populacional.
Intervalo de Confiança
Onde SE é o erro padrão, que nada mais é do que o desvio padrão de X dividido pela raiz quadrada de n.
## No R:
pnorm(2) - pnorm(-2)
[1] 0.9544997Intervalo de Confiança
## No R:
# 99%
z <- qnorm(0.995)
[1] 2.575829
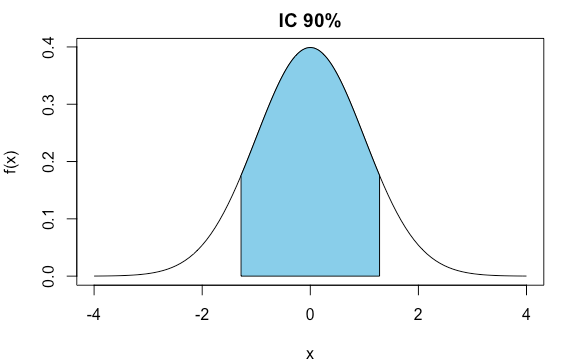
# 95%
z <- qnorm(0.975)
[1] 1.959964
# 90%
z <- qnorm(0.95)
[1] 1.644854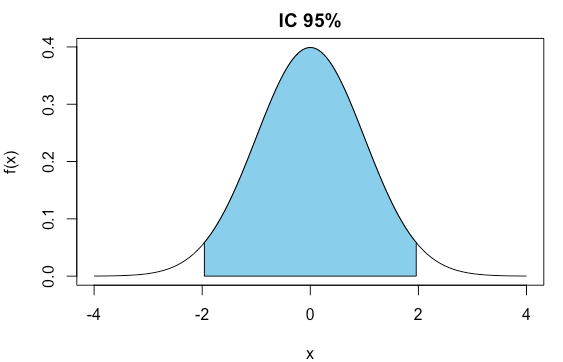
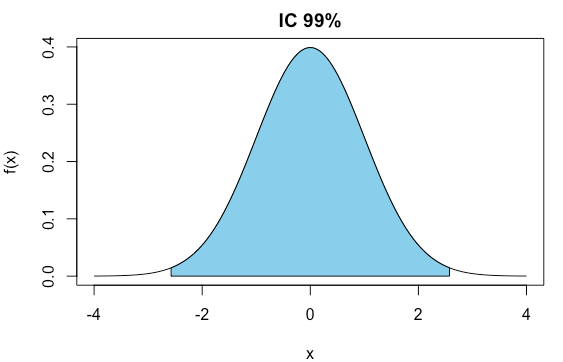
Simulações de Monte Carlo
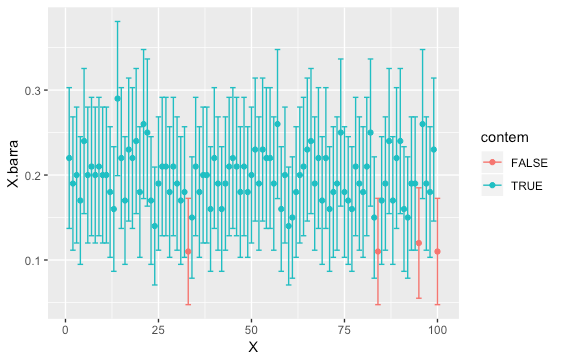
Simulações de Monte Carlo
# Verificando que o tamanho da amostra influencia
p <- 0.2
N.repeticoes <- 10000
N.amostra <- 10
X <- sample(c(0,1), size=N.amostra, replace=TRUE, prob=c(1-p, p))
X.barra <- mean(X)
SE.estimado <- sqrt(X.barra*(1-X.barra)/N.amostra)
c(X.barra - 2*SE.estimado, X.barra + 2*SE.estimado)
IC.aux <- replicate(N.repeticoes, {
X <- sample(c(0,1), size=N.amostra, replace=TRUE, prob=c(1-p, p))
X.barra <- mean(X)
SE.estimado <- sqrt(X.barra*(1-X.barra)/N.amostra)
LS <- X.barra + 2*SE.estimado
LI <- X.barra - 2*SE.estimado
between(p, X.barra - 2*SE.estimado, X.barra + 2*SE.estimado)
})
Testes estatísticos
Teste de hipóteses:
- ferramenta que permite validar (aceitar) ou refutar (rejeitar) uma alguma afirmação prévia.
- auxilia na decisão a ser tomada

Hipóteses:
P-valor:
é o menor nível de significância para o qual a hipótese nula é rejeitada.
Nível de significância:
Testes estatísticos
P-valor:
Comumente, o p-valor é utilizado para avaliar a significância de um teste de hipóteses
- Se o p-valor for menor que 5%, então o resultado é estatísticamente significante
- Se o p-valor for menor que 1%, então o resultado é estatísticamente significante
Testes estatísticos
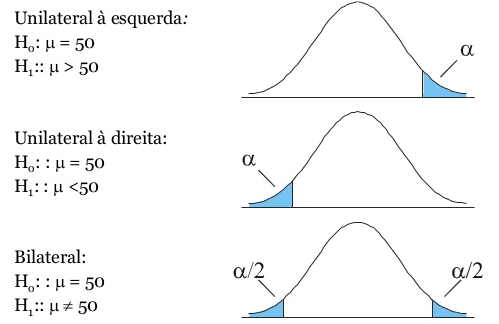
Teste de hipóteses: podem ser bilaterais ou unilaterais.
Exemplo para a média populacional
Testes estatísticos
Teste t
Suponha que estamos interessados em investigar a média populacional de um determinado fenômeno.
Onde s representa o valor estimado do desvio padrão e representa o valor estimado da média.
Utilizamos este teste quando desconhecemos o valor verdadeiro da variância populacional e a amostra é pequena n < 30
Testes estatísticos - Exemplos
Exemplo: Verificar a quantidade de calorias num determinado produto. A empresa informa que a média de calorias de seu produto é de 30 kcal/g, mas a ANVISA afirma que é maior.
## No R:
# amostra de 25 produtos
calorias = c(30.05,29.38,28.45,31.22,31.07,34.44,34.50,34.48,31.75,30.59,
31.92,31.76,30.25,33.28,33.40,31.46,31.43,32.92,
29.91,33.63,27.98,33.07,31.01,29.85,29.70)
t.test(calorias,mu=30,alternative ="greater")
Testes estatísticos - Exemplos
O
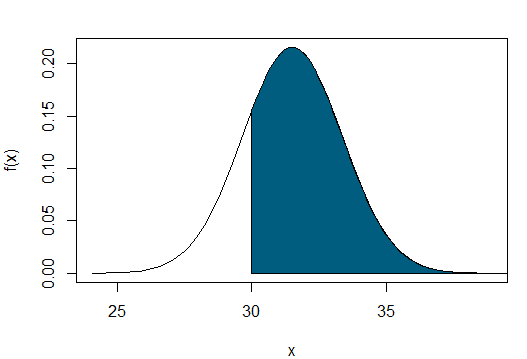
Calcule o intervalo de confiança, a estatística de teste e use o comando t.test do R para chegar a uma conclusão
Testes estatísticos - Exemplos
## No R:
# amostra de 25 produtos
calorias = c(30.05,29.38,28.45,31.22,31.07,34.44,34.50,34.48,31.75,30.59,
31.92,31.76,30.25,33.28,33.40,31.46,31.43,32.92,29.91,
33.63,27.98,33.07,31.01,29.85,29.70)
# IC
N.amostra <- length(calorias)
calorias.barra <- mean(calorias)
se.calorias <- sd(calorias)/sqrt(N.amostra)
IC <- c((calorias.barra - 2*se.calorias),(calorias.barra + 2*se.calorias))
# Estatística de teste
t.score = (mean(calorias) - 30)/se.calorias
# Teste t
t.test(calorias,mu=30,alternative ="greater")
Testes estatísticos
Teste para a proporção
Suponha que estamos interessados em investigar a média populacional de um determinado fenômeno.
Onde s representa o valor estimado do desvio padrão e representa o valor estimado da proporção.
Exemplo: avaliar se proporção de crianças do sexo masculino nascidas em 2016 é de 50%.
Testes estatísticos - Exemplos
Segundo dados do Registro Civil (IBGE), dos 2.803.080 nascimentos 1.435.631 foram de homens
Testes estatísticos - Exemplos
# Teste para proporção
N.amostra <- 2803080
prop.estimada <- 1435631/2803080
se.prop <- sqrt((prop.estimada*(1-prop.estimada))/N.amostra)
IC <- c((prop.estimada - 2*se.prop),(prop.estimada + 2*se.prop))
IC <- c((prop.estimada - 1.96*se.prop),(prop.estimada + 1.96*se.prop))
# Estatística de teste
t.score = (prop.estimada - 0.5)/se.prop
t.score^2
# Teste - t
prop.test(1435631,n=2803080,p=0.5)O
Testes estatísticos - Exemplos
Exemplo: tianeptina é um antidepressivo. Aplicou-se a droga em dois grupos de pacientes e quantificou o nível de depressão através da escala de Montgomery-Asberg, em que os valores maiores indicam maior gravidade da depressão.
## No R:
placebo <- c(6,33,21,26,10,29,33,29,37,15,2,21,7,26,13,18)
tianeptina <- c(10,8,17,4,17,14,9,4,21,3,7,10,29,13,14,2)
t.test(tianeptina,placebo,alternative ="less")
Welch Two Sample t-test
data: tianeptina and placebo
t = -2.7788, df = 26.343, p-value = 0.004965
alternative hypothesis: true difference in means is less than 0
95 percent confidence interval:
-Inf -3.478563
sample estimates:
mean of x mean of y
11.375 20.375 Testes estatísticos - Exemplos
Exemplo: tianeptina é um antidepressivo. Aplicou-se a droga em dois grupos de pacientes e quantificou o nível de depressão através da escala de Montgomery-Asberg, em que os valores maiores indicam maior gravidade da depressão.
## No R:
placebo <- c(6,33,21,26,10,29,33,29,37,15,2,21,7,26,13,18)
tianeptina <- c(10,8,17,4,17,14,9,4,21,3,7,10,29,13,14,2)
t.test(tianeptina,placebo,alternative ="less")
Welch Two Sample t-test
data: tianeptina and placebo
t = -2.7788, df = 26.343, p-value = 0.004965
alternative hypothesis: true difference in means is less than 0
95 percent confidence interval:
-Inf -3.478563
sample estimates:
mean of x mean of y
11.375 20.375