Raíra Marotta
Estatística
Curso Big Data e Data Science
Aula 5 - Probabilidade
Introdução
Suponha que uma urna tenha 4 bolas azuis e 6 vermelhas.
- Qual é a probabilidade de extrairmos uma bola vermelha da urna?
- Qual é a probabilidade de extrairmos duas bolas azuis?
## No R:
# Simulando uma urna --
urna <- rep( c("vermelha", "azul"), times = c(6,4))
[1] "vermelha" "vermelha" "vermelha" "vermelha"
[5] "vermelha" "vermelha" "azul" "azul"
[9] "azul" "azul"
#Extraindo duas bolas
sample(urna, 2)
[1] "vermelha" "azul" Simulação de Monte Carlo
Suponha a retirada de uma bola da urna repetidas vezes. Rode o código abaixo e verifique o que acontece com as proporções

## No R
n <- 10
Repete <- replicate(n, sample(urna, 1))
table(Repete)
prop.table(table(Repete))
n <- 100
Repete <- replicate(n, sample(urna, 1))
table(Repete)
prop.table(table(Repete))
n <- 1000
Repete <- replicate(n, sample(urna, 1))
table(Repete)
prop.table(table(Repete))
Probabilidade Condicional
Suponha agora que a bola não volta a urna após ser sorteada.
- Dado que a primeira bola sorteada foi azul, qual a probabilidade da segunda ser azul novamente?
- Essa probabilidade é a mesma do caso em que a bola volta para a urna ?
## No R
# Sorteio com repetição ----
sample(urna, 11, replace = TRUE)
[1] "azul" "azul" "azul" "azul" "azul"
[6] "vermelha" "vermelha" "vermelha" "vermelha" "vermelha"
[11] "vermelha"
# Sorteio sem repetição ----
sample(urna, 11, replace = FALSE)
Error in sample.int(length(x), size, replace, prob) :
cannot take a sample larger than the population when 'replace = FALSE'Probabilidade Condicional
## No R
library(gtools)
naipes <- c("ouros", "espadas", "copas", "paus")
cartas <- c("Ás", "2", "3", "4", "5", "6", "7", "8", "9", "10", "Valete", "Rei", "Rainha")
deck <- expand.grid(cartas=cartas, naipes=naipes)
deck <- paste(deck$cartas,deck$naipes)
# Verificando a probabilidade de sortear um Ás
as <- paste("Ás", naipes)
mean(deck %in% as)
# Qual a probabilidade de sortear um Ás dado que a primeira carta sorteada foi um Ás?
combinacoes_possiveis <- permutations(52, 2, v = deck)
sum(combinacoes_possiveis[,1] %in% as & combinacoes_possiveis[,2] %in% as) /
sum(combinacoes_possiveis[,1] %in% as)
[1]0.05882353
Permutação x Combinação
Permutação: a ordenação importa.
Combinação: a ordenação não importa.
Exemplo: Suponha um jogo em que o jogador jogará a moeda 2 vezes. Se a face voltada para cima no primeiro lançamento for cara, ele ganha 2 pontos. Se for cara no segundo lançamento 1 ponto e se tirar 2 caras, 0 pontos.
## No R:
library(gtools)
perm <- permutations(2,2,c("cara", "coroa"),repeats.allowed=TRUE)
[,1] [,2]
[1,] "cara" "cara"
[2,] "cara" "coroa"
[3,] "coroa" "cara"
[4,] "coroa" "coroa"## No R:
combina <- combinations(2,2,c("cara", "coroa"),repeats.allowed=TRUE)
[,1] [,2]
[1,] "cara" "cara"
[2,] "cara" "coroa"
[3,] "coroa" "coroa"Exemplo do Aniversário
Suponha que desejamos saber qual a probabilidade de duas pessoas dessa turma fazerem aniversário no mesmo dia.
## No R:
n <- 20
mesmo_bday <- function(n){
bdays <- sample(1:365, n, replace=TRUE)
any(duplicated(bdays))
}
# Verifica quantas amostras, em média,
# tiveram pessoas com aniversários repetidos
N <- 1000
results <- replicate(B, mesmo_bday(n))
mean(results)
compute_prob <- function(n, N = 1000){
aux.prob <- replicate(N, mesmo_bday(n))
mean(aux.prob)
}
n <- seq(1,60)
prob <- sapply(n, compute_prob)
plot(n, prob, pch = 20)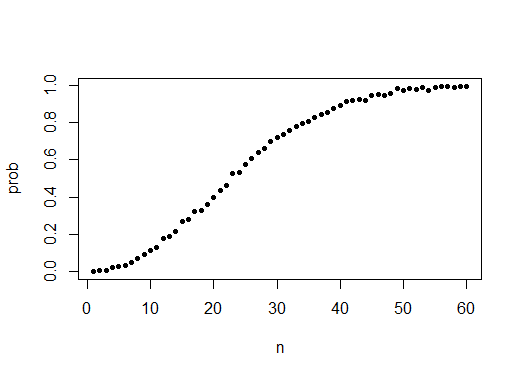
Exercício
Temos uma urna com 3 bolas verdes, 2 azuis, 5 brancas.
- Qual a probabilidade de sortearmos uma bola verde?
- Qual a probabilidade de sortearmos uma bola vermelha?
- Qual a probabilidade NÃO sortearmos uma bola branca?
- Dado que retiramos uma bola verde no primeiro experimento. Qual a probabilidade de retirarmos novamente uma bola verde?