The high-dimensional latent structure of visual cortex representations

Brice Ménard

Raj Magesh Gauthaman

Michael F. Bonner

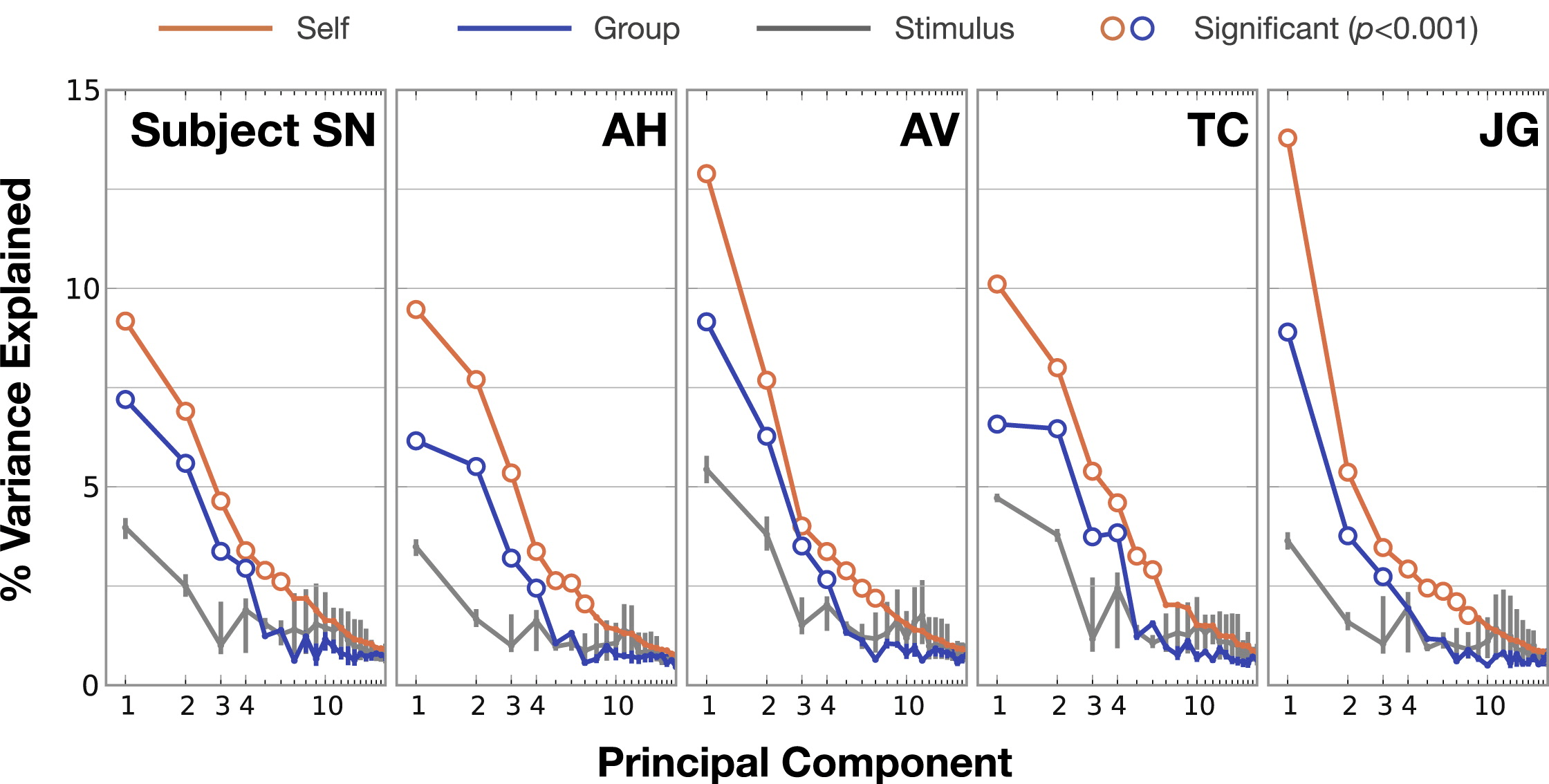
1

2, 1

1

1

2

light enters your eyes

1

signals travel to visual cortex

2

cortical processing

3

perceptual experience

4

How can we understand visual representations?

How can we understand visual representations?

“ambient”
dimensions

  • single neurons
  • voxels from fMRI
  • EEG/MEG sensors
  • abstract dimensions

neural response

stimulus

vector of neuron responses

neuron 1

neuron 4

neuron N

...

How can we understand visual representations?

all axes are orthogonal (90°)

neuron 2

neuron 1

neuron 3

neuron 4

...

neuron N

neuron 2

neuron 1

neuron 3

neuron 4

...

neuron N

has many people

has no people

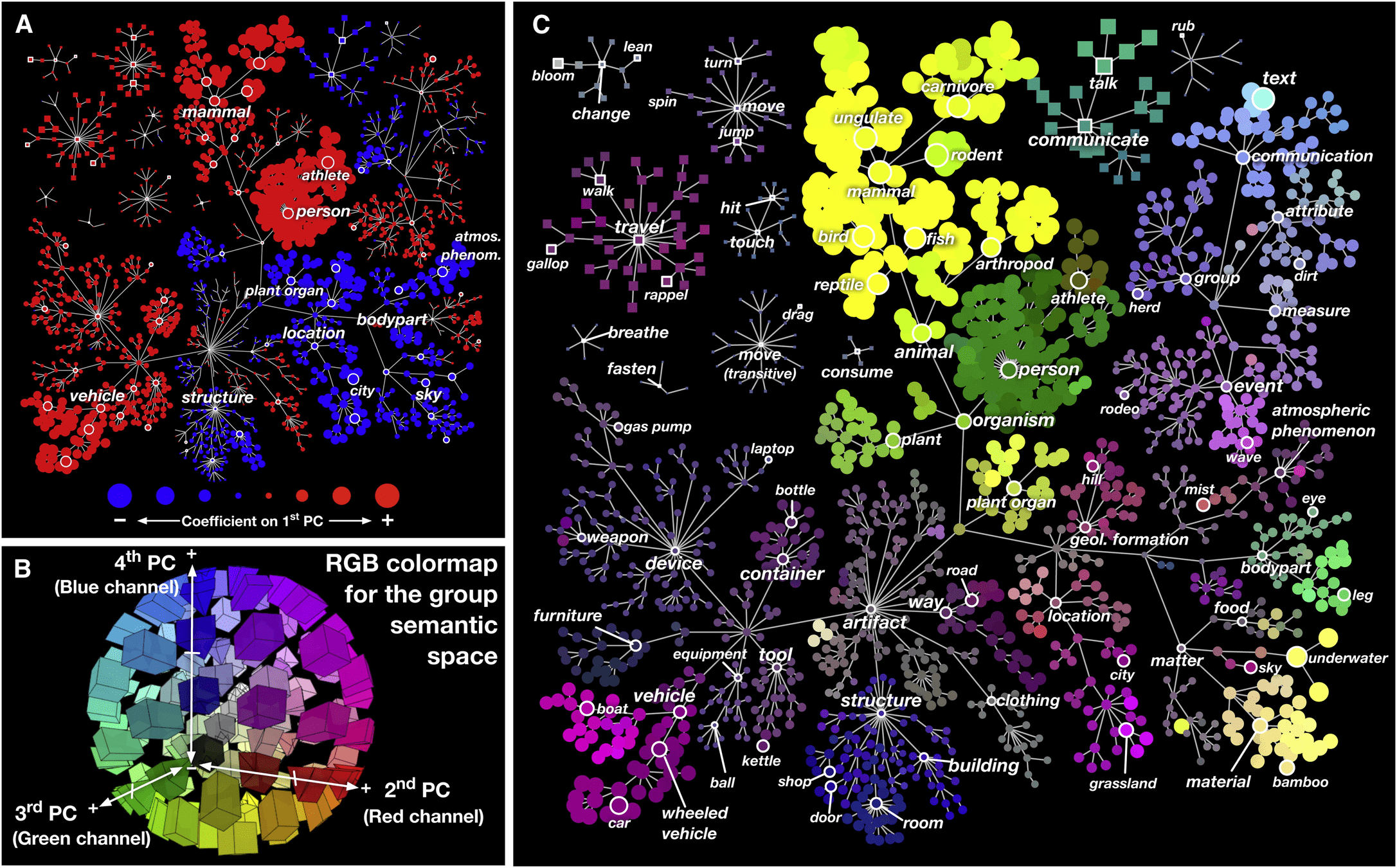
A common approach is to study latent dimensions.

“latent”
dimension

How can we understand visual representations?

all axes are orthogonal (90°)

A common approach is to study latent dimensions.

Long et al. (2015)

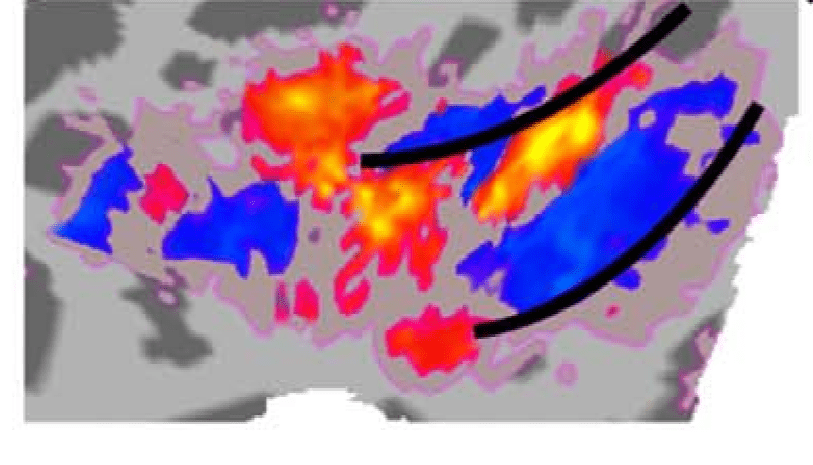
“animacy” dimension in human visual cortex

A common approach is to study latent dimensions.

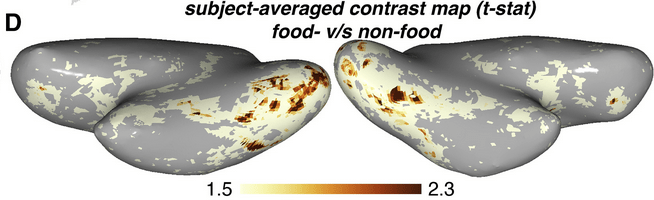
“food” dimension in human visual cortex

Khosla et al. (2022)

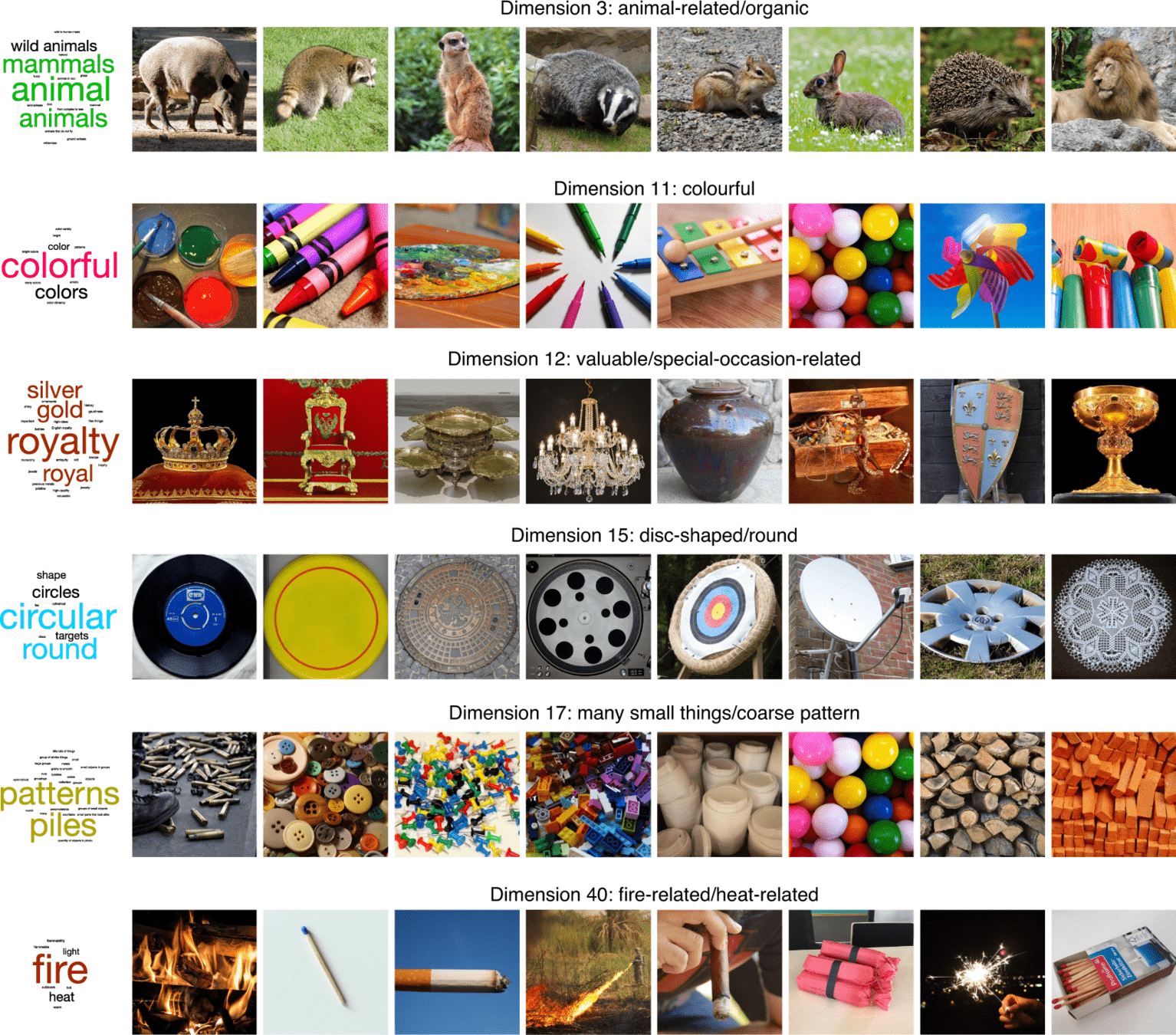
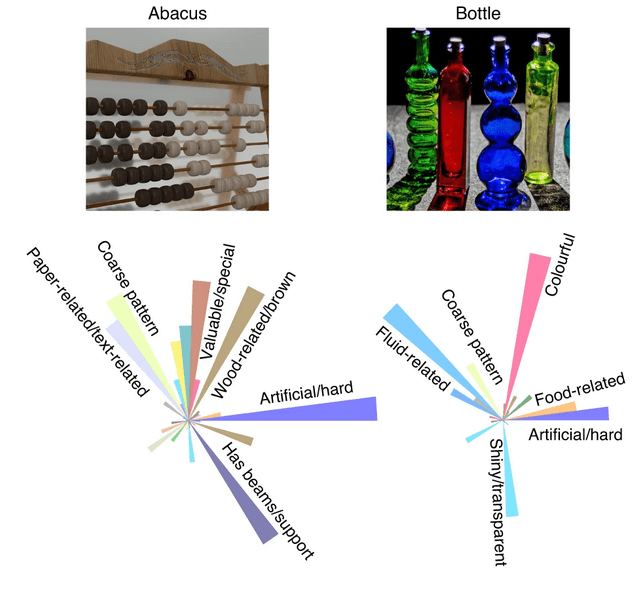
A common approach is to study latent dimensions.

66 dimensions of mental object representations (inferred from behavioral data)

Hebart et al. (2020)

A common approach is to study latent dimensions.

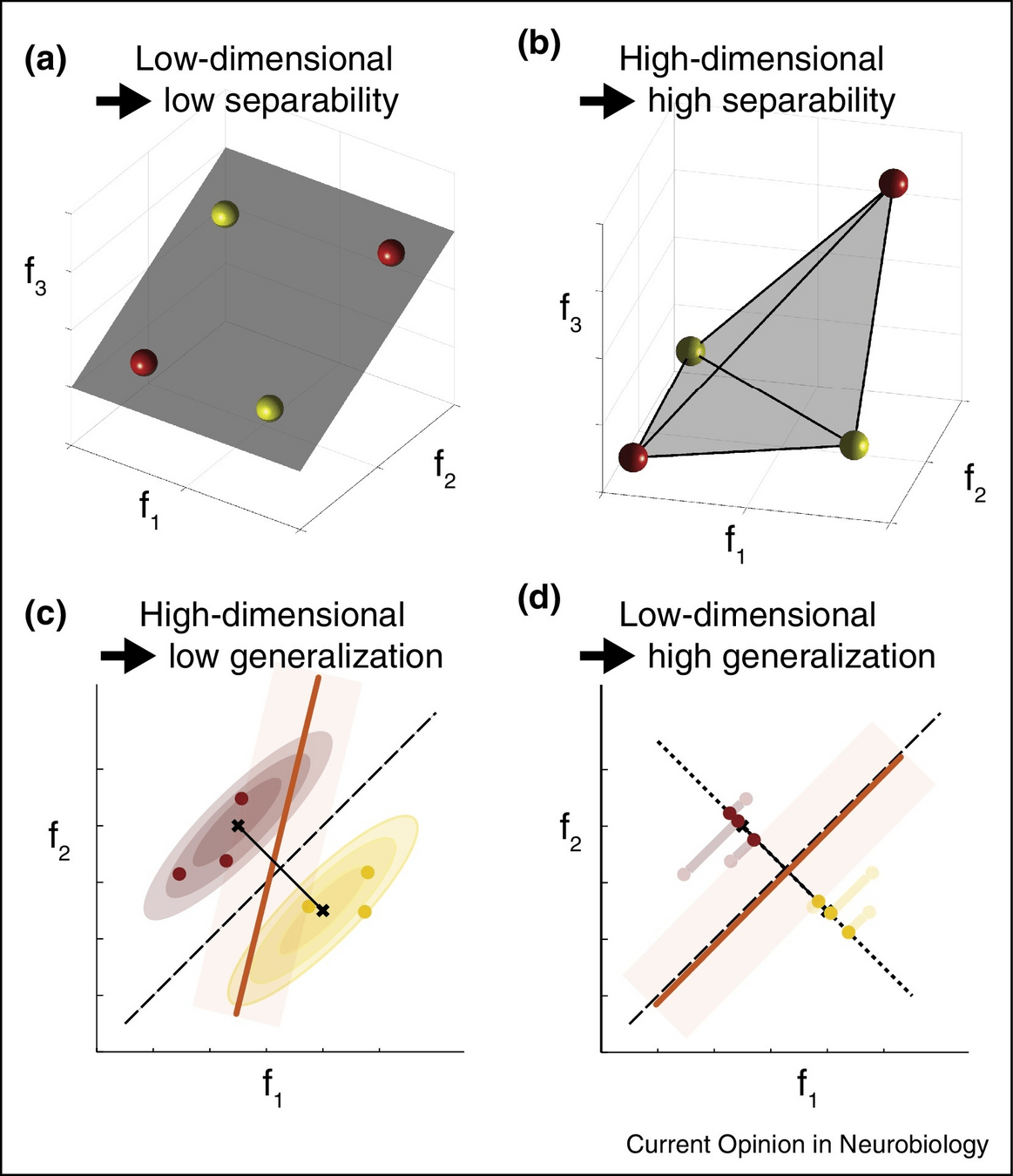
When does this approach make sense?

data manifold spans a low-dimensional subspace

d_\text{latent}
d_\text{ambient}
<<

data spans both ambient dimensions

data lives in a 1-D subspace

“latent dimension”

A common approach is to study latent dimensions.

When does this approach make sense?

A common approach is to study latent dimensions.

When does this approach make sense?

Catalog all the latent dimensions!

d_\text{latent}
d_\text{ambient}
<<

data manifold spans a low-dimensional subspace

  • remove noise
  • visualize data
  • extract salient patterns

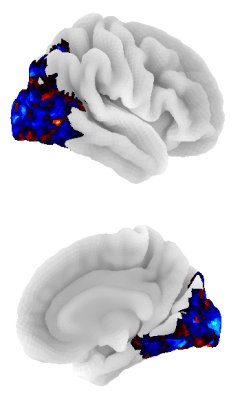
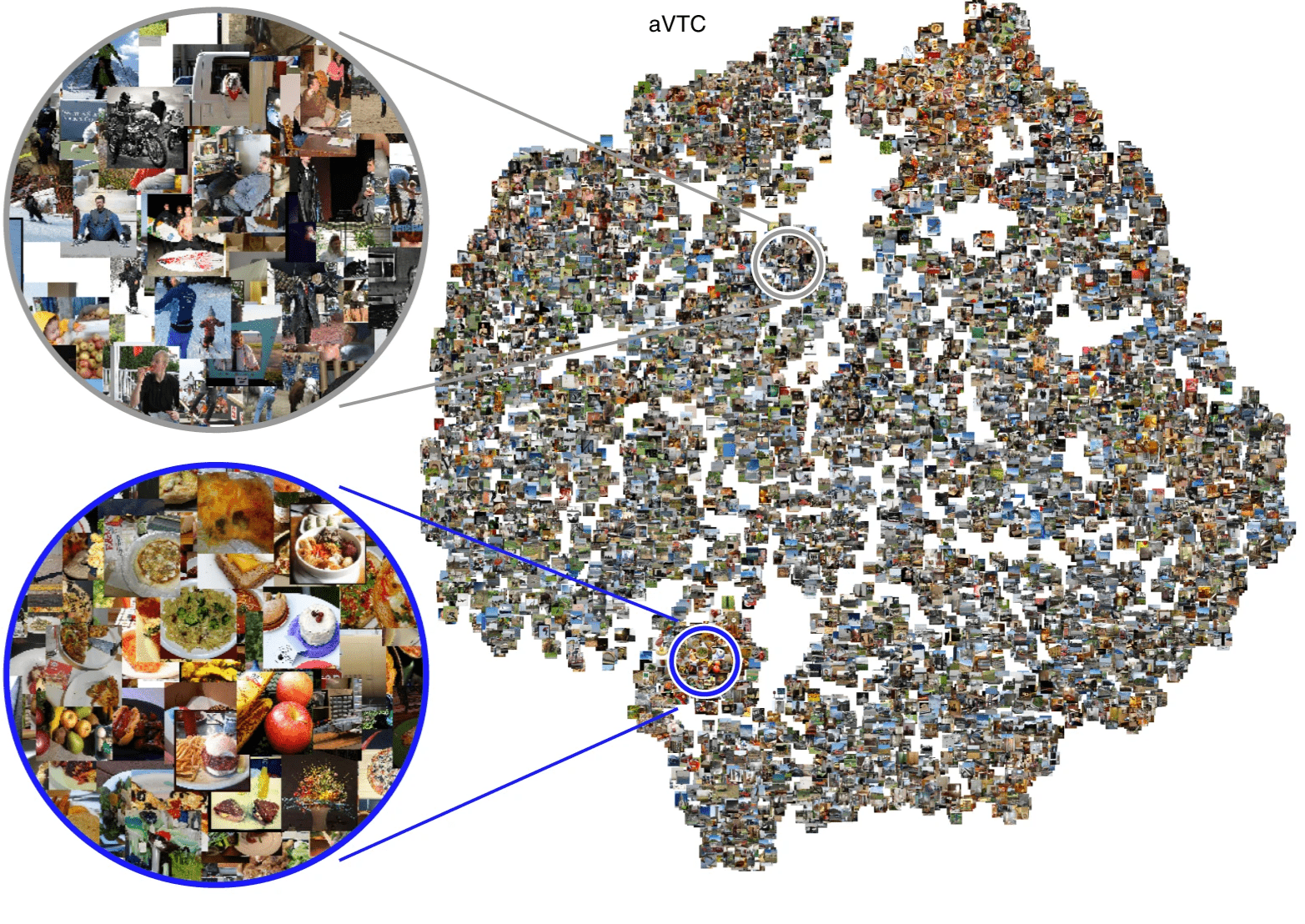
“ [...] the topographies in ventrotemporal cortex (VTC) that support a wide range of stimulus distinctions [...] can be modeled with 35 basis functions”

The visual code is found to be low-dimensional.

Haxby et al. (2011)

“Thus, our fMRI data are sufficient to recover semantic spaces for individual subjects that consist of 6 to 8 dimensions.”

Huth et al. (2012)

The visual code is found to be low-dimensional.

The visual code is found to be low-dimensional.

Hebart et al. (2020)

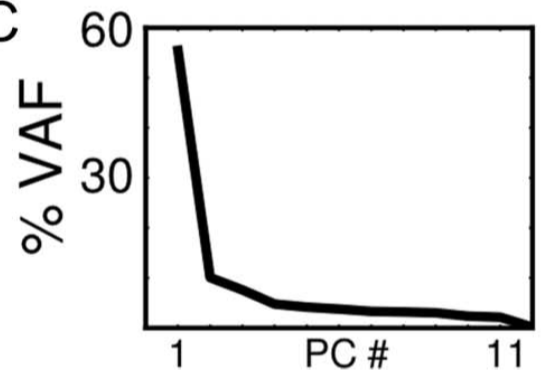
66 dimensions

Principal Component Analysis

Non-negative Matrix Factorization

Sparse Positive Similarity Embedding

dimensions stimuli system method
Haxby et al. (2011) 35 movies human ventrotemporal cortex PCA
Huth et al. (2012) 6-8 (4 shared) movies human cortex PCA
Lehky et al. (2014) 60 (~87 estimate) objects macaque inferotemporal cortex PCA
Tarhan et al. (2020) 5 visual actions human cortex k-means
Hebart et al. (2020) 49 objects human behavior SPoSE
Khosla et al. (2022) 20 (5 reliable) scenes human ventral visual stream NMF
Hebart et al. (2023) 66 objects human behavior SPoSE

The visual code is found to be low-dimensional.

A lot of converging evidence that visual representations are low-dimensional across stimuli, species, and methods

~87 dimensions of object representations in monkey inferotemporal (IT) cortex

“A progressive shrinkage in the intrinsic dimensionality of object response manifolds at higher cortical levels might simplify the task of discriminating different objects or object categories.”

Computational goal of cortex: compress dimensionality.

Lehky et al. (2014)

Previous work has found that dimensionality is bounded.

neural representations

mental representations

What if dimensionality doesn't saturate with dataset size?

Hebart et al. (2020)

Lehky et al. (2014)

But high-dimensional codes have benefits too.

Fusi et al. (2016)

high representational capacity, expressive

makes learning new tasks easier

Elmoznino & Bonner (2024)

Could visual representations be more high-dimensional than previously found?

We now have very large-scale, high-quality datasets.

Outline of today's talk

Visual cortex representations are high-dimensional.

1

They are self-similar over a huge range of spatial scales.

2

The same geometry underlies mental representations of images.

3

Gauthaman, Menard & Bonner, under review

Gauthaman, Menard & Bonner, in preparation

The Natural Scenes fMRI dataset

Allen et al. (2022)

8 subjects

7 T fMRI

10,000 images (repeated 3×)

from the COCO dataset

"Have you seen this image before?"

continuous recognition

Credit: NordicNeuroLab

fMRI

functional magnetic resonance imaging

resolution

~1 mm

~3 s

 

coarse measure of neural activity

Ideal dataset to characterize dimensionality

Allen et al. (2022)

  • very large-scale

  • naturalistic stimuli

  • complex scenes

How can we estimate dimensionality?

  • same geometry
  • new perspective

rotation

Principal Component Analysis

rank 1

rank 2

latent dimensions

ambient dimensions

high variance

low variance

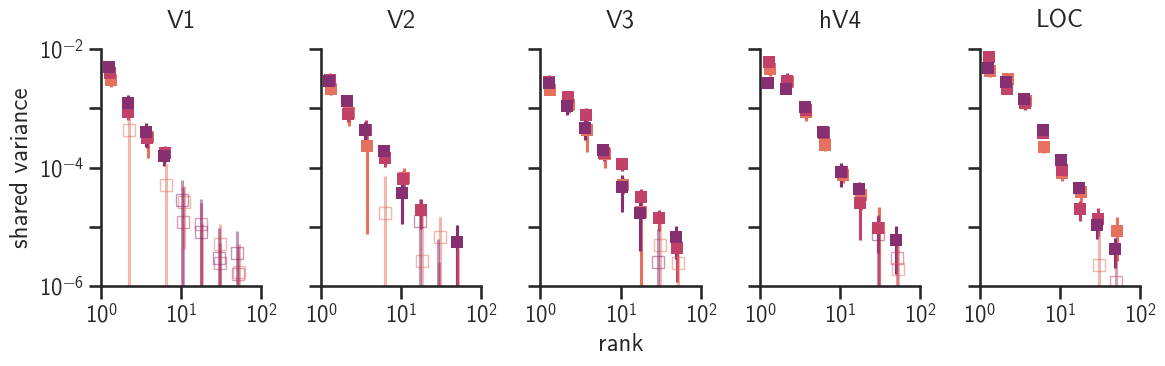
Key statistic: the covariance spectrum

latent dimensions sorted by variance

variance along the dimension

  • logarithmic scales
  • multiple orders of magnitude

low-dimensional code

high-dimensional code

no variance along other dimensions

variance along many dimensions

"core subset" of relevant dimensions

Key statistic: the covariance spectrum

variance along each dimension

Should we just apply PCA?

stimulus-related signal

trial-specific noise

generalizes

... across stimulus repetitions

... to novel images

X_\text{train}
Y_\text{train}

trial 1

trial 2

neurons (or) voxels

stimuli

\text{cov}\left(X_\text{train}, Y_\text{train}\right) = U \Sigma V^\top

Learn latent dimensions

Step 1

Step 2

Evaluate reliable variance

\hat{\Sigma} = \text{cov}\left(X_\text{test} U, Y_\text{test} V\right)
X_\text{test}
Y_\text{test}

If there is no reliable signal in the data, expected value = 0

Cross-decomposition measures stimulus-related signal.

The math of cross-decomposition

\operatorname{cov}(X, Y) = \frac{1}{n} \left(X^\top - \bar{X}\right) \left(Y^\top - \bar{Y}\right)
\operatorname{cov}(X, Y) = U \Sigma V^\top
= \sum_{i=1}^n \sigma_i U_i V_i^\top

the (cross-)covariance matrix

its singular value decomposition

"splitting a matrix into the sum of rank-1 matrices"

The math of cross-decomposition

UV^\top = \operatorname{argmin}_{Q \in SO(n)} || X - YQ ||_F
  • Procrustes
  • PLS-SVD (Partial Least Squares Singular Value Decomposition)
  • hyperalignment (Haxby et al., 2011)
  • the optimal rotation that aligns X to Y
  • preserves geometry (shape; spectrum)
  • "spectral decomposition of the cross-covariance"
QQ^\top = Q^\top Q = I

PCA vs cross-decomposition

logarithmic binning + 8-fold cross-validation

PCA always finds some variance along each ambient dimension ...

... but cross-decomposition
has an expected value of 0.

PCA

cross-decomposition

If there is no stimulus-related signal

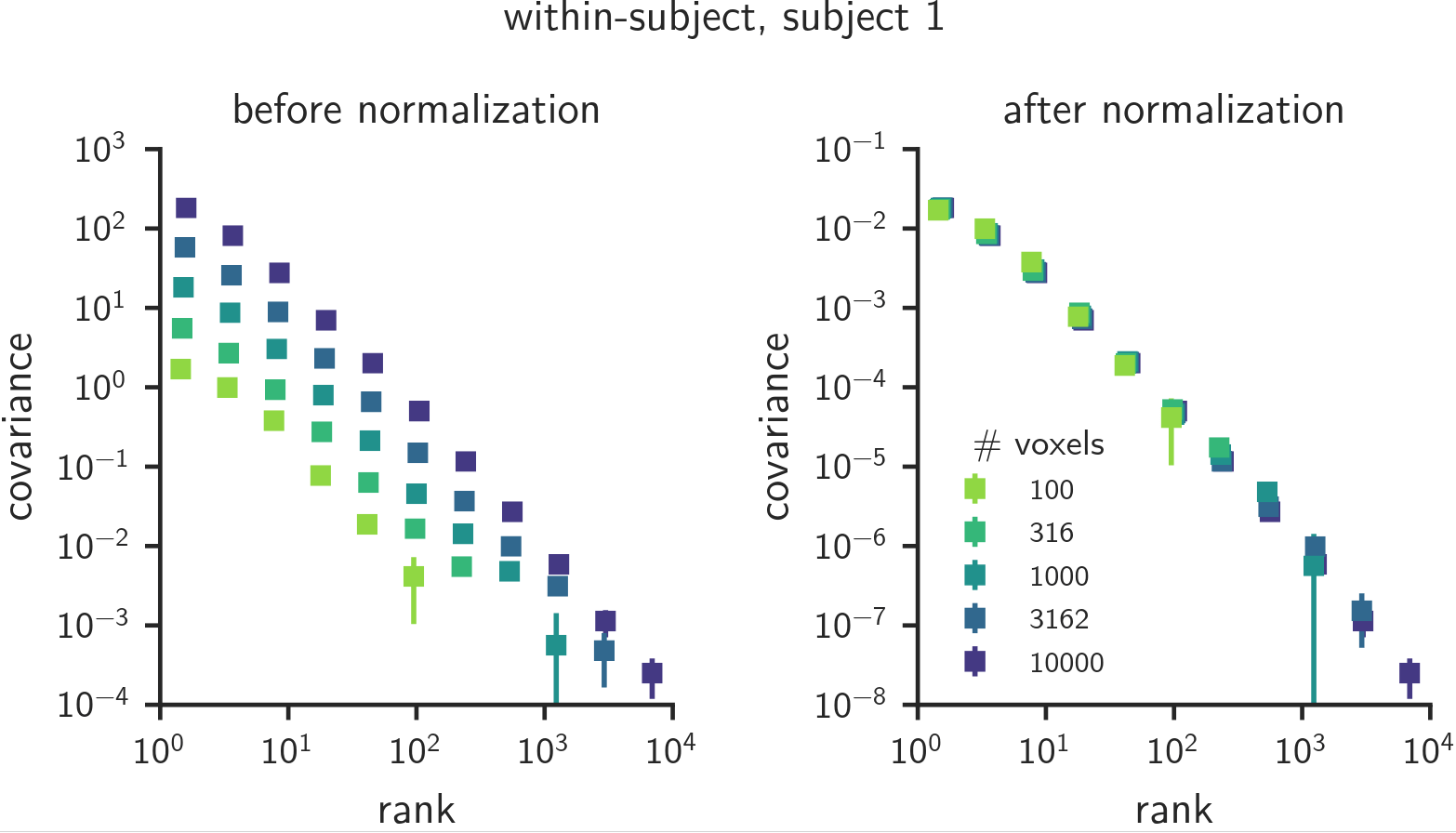
The covariance is normalized by the number of voxels.

The spectrum depends on the size of the dataset.

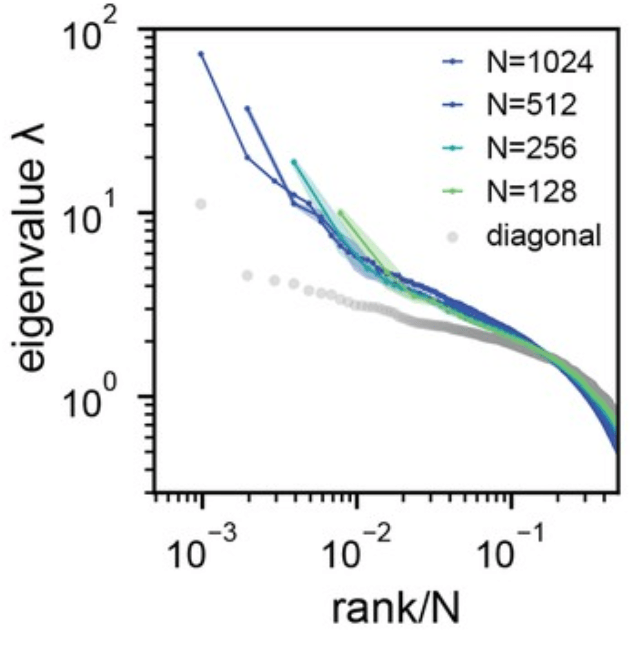
Our cross-validated covariance spectra

reliable variance on the test set

latent dimensions sorted by variance on the training set

Our cross-validated covariance spectra

vs

\text{covariance} \propto \left(\text{rank}\right)^\alpha

binned logarithmically to increase SNR

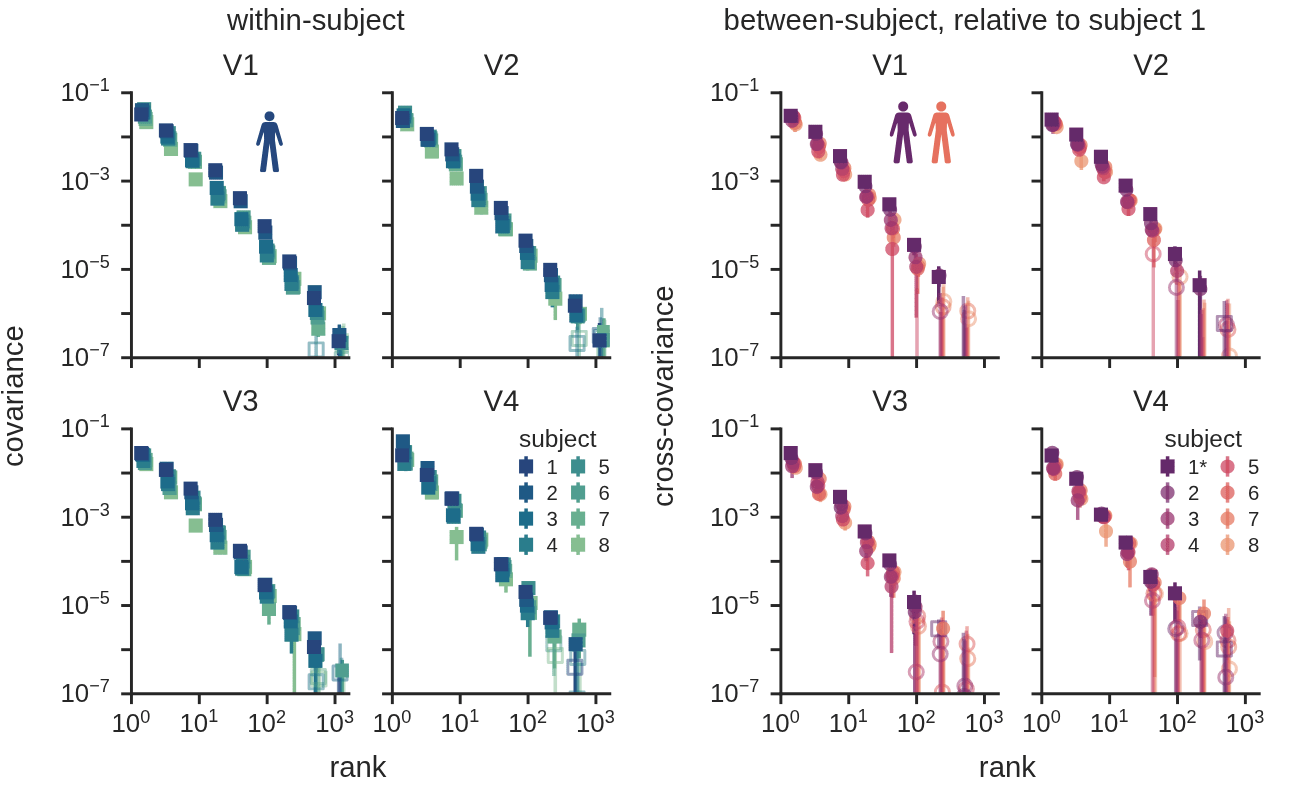
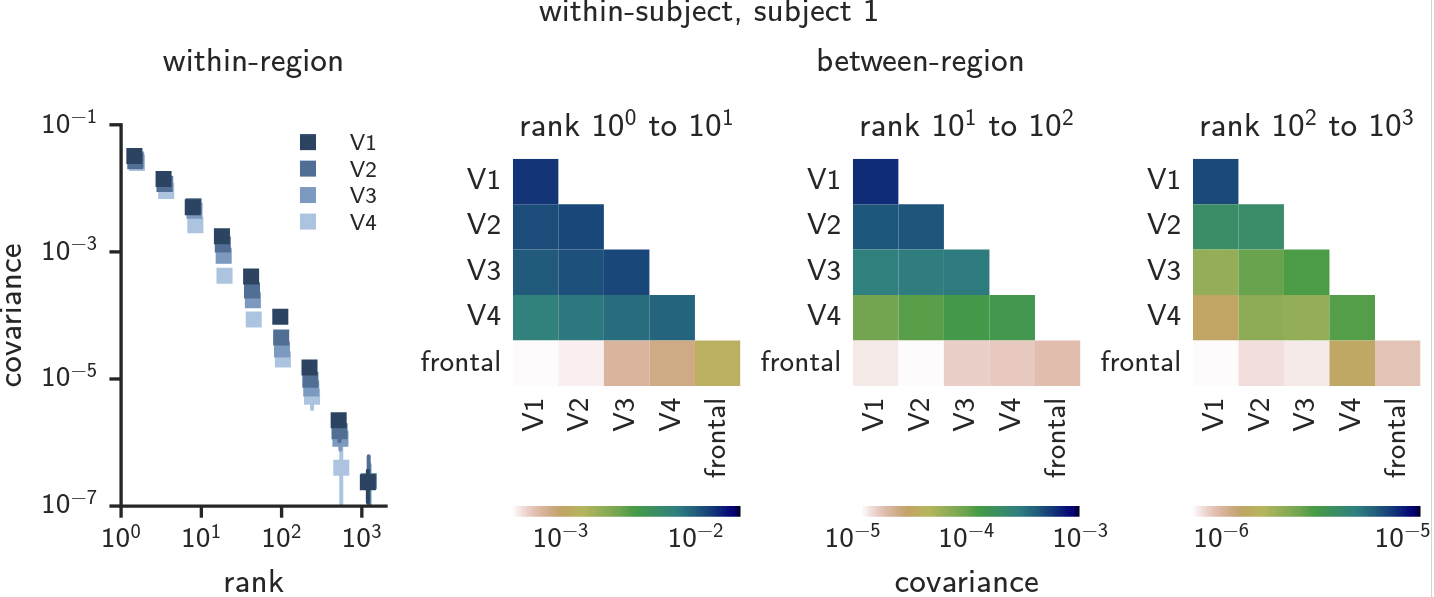
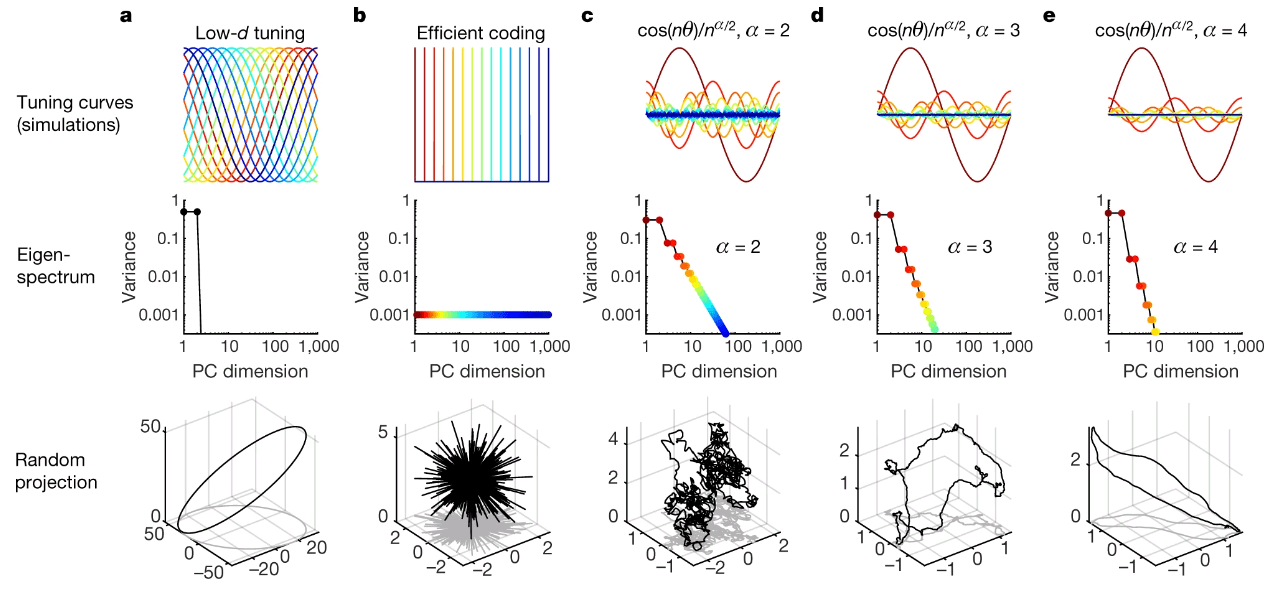
Visual cortex has power-law covariance spectra.

\text{covariance} \propto \left(\text{rank}\right)^\alpha
  • Not limited to a “core subset”
    All dimensions are used, but weighted differently
     
  • Scale-free
    All dimensions have variance distributed in the same way
     
  • No evidence of a break
    More data, more dimensions?

Visual cortex has power-law covariance spectra.

artifact of analyzing a large ROI?

High-dimensional across multiple levels of the visual hierarchy

dimensions stimuli system method
Huth et al. (2012) 6-8 (4 shared) movies human cortex PCA
Khosla et al. (2022) 20 (5 reliable) scenes human ventral visual stream NMF

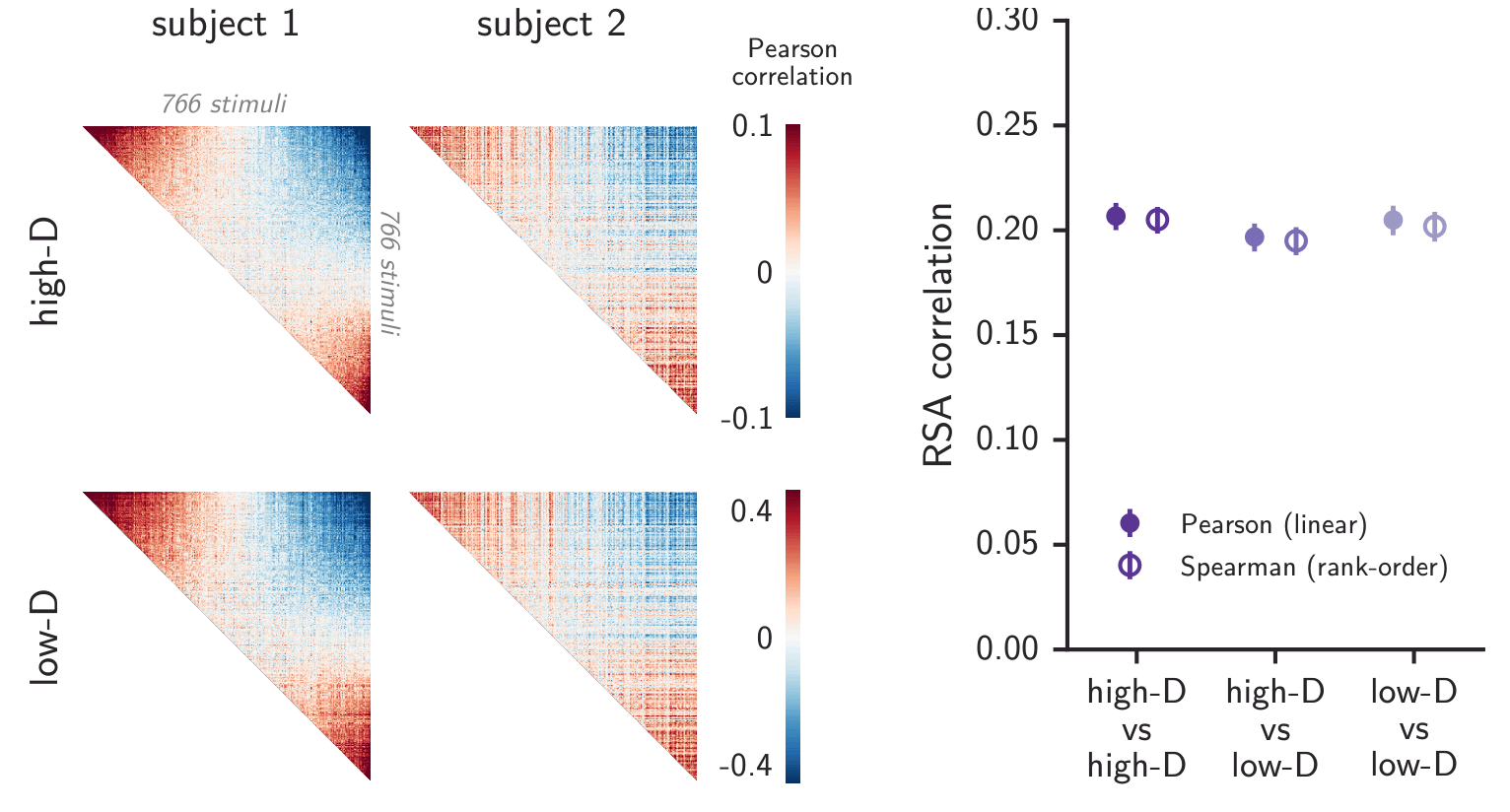
Is this high-dimensional structure shared across people?

vs

reliable, and shared

reliable, but idiosyncratic

Cross-decomposition still works!

generalizes

... across stimulus repetitions

... to novel images

... across participants

X_\text{train}
Y_\text{train}

subject 1

subject 2

neurons (or) voxels

stimuli

\text{cov}\left(X_\text{train}, Y_\text{train}\right) = U \Sigma V^\top

Learn latent dimensions

Step 1

Step 2

Evaluate reliable variance

\hat{\Sigma} = \text{cov}\left(X_\text{test} U, Y_\text{test} V\right)
X_\text{test}
Y_\text{test}
\frac{\text{cov}(S_1, S_2)}{\sqrt{\text{cov}(S_1, S_1) \text{cov}(S_2, S_2)}}

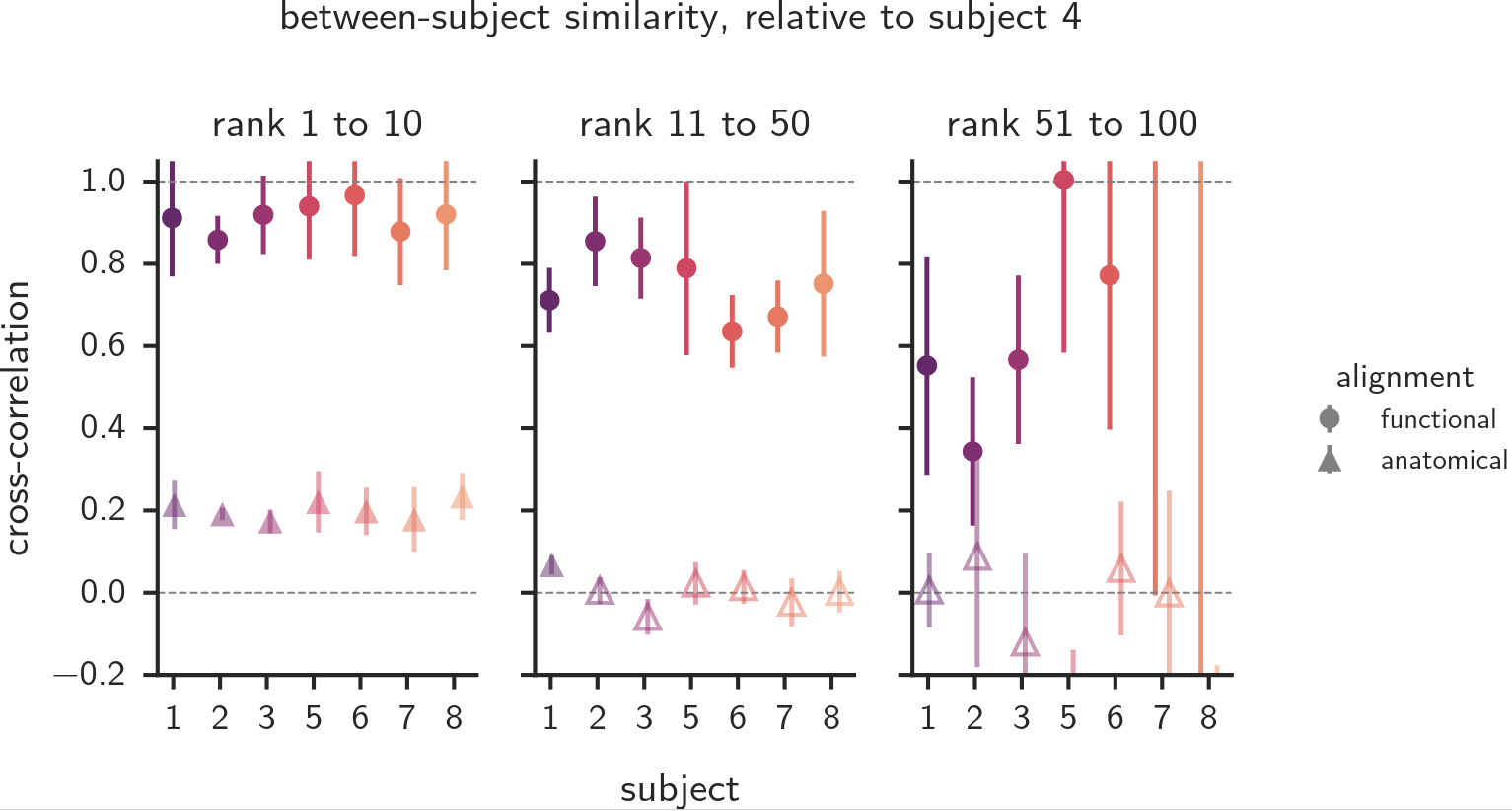
Functional – not anatomical – alignment is required

Cross-individual covariance spectra

Shared high-dimensional structure across individuals

reliable, and shared

Are these spectra just an artifact of the method used?

No, they represent real high-dimensional signal!

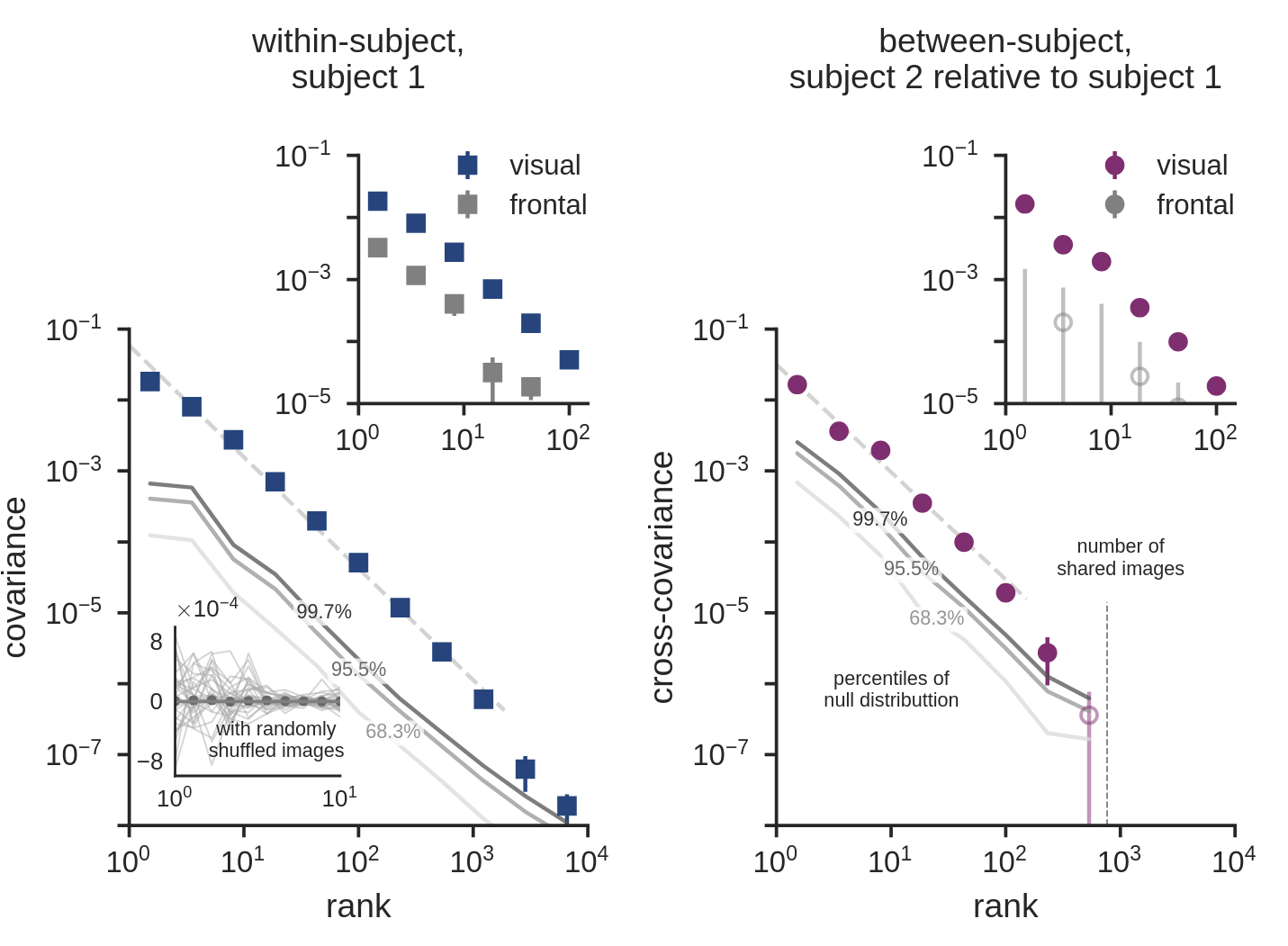
Visual cortex representations are high-dimensional.

1

vs

vs

striking universality across individuals

high-dimensional

power-law covariance

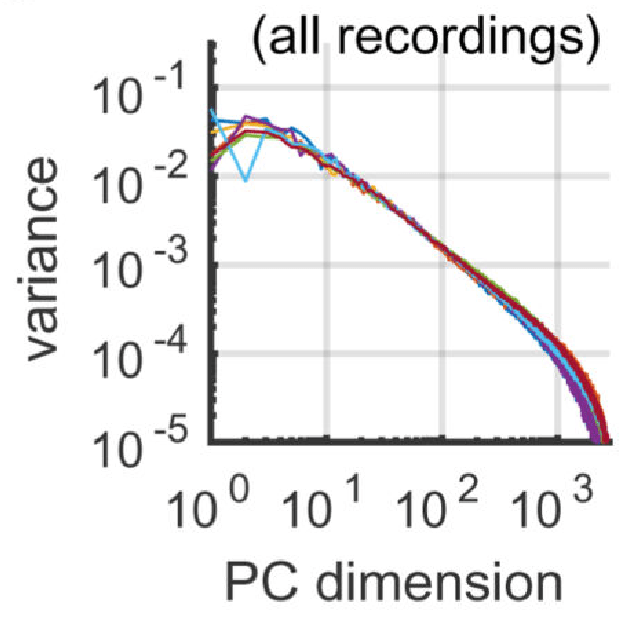
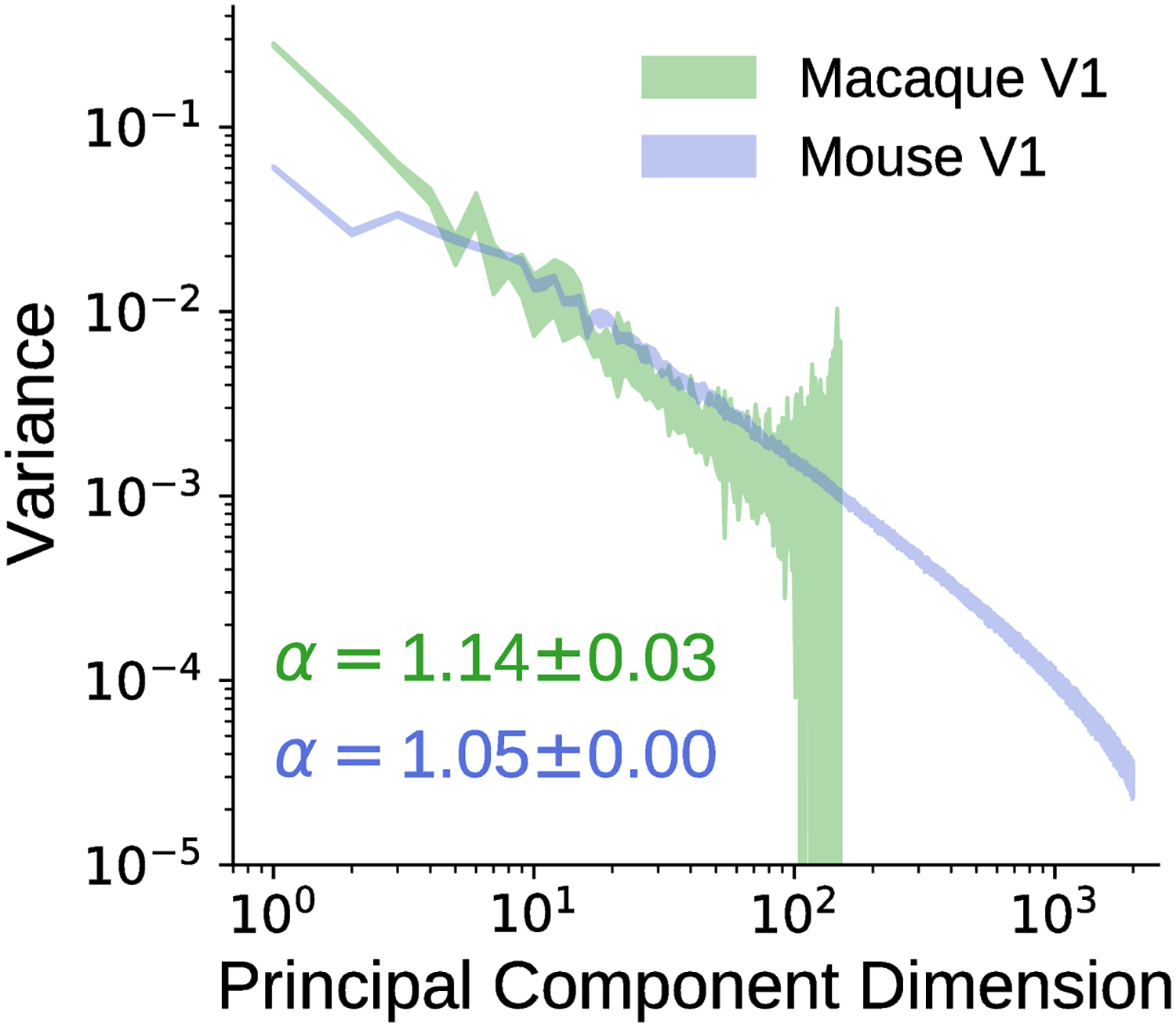
Similar power-law spectra in mouse V1

  • calcium imaging
  • 10,000 neurons
  • 2,800 natural images

Stringer et al. (2019)

6 mice

calcium imaging

 

~10,000 V1 neurons

~2,800 natural images

Similar power-law spectra in mouse V1

Similar neural population statistics

  • in different species,
  • across imaging methods,
  • at very different resolutions.


Why does this happen?

also shared across individuals!

Outline of today's talk

Visual cortex representations are high-dimensional.

1

They are self-similar over a huge range of spatial scales.

2

The same geometry underlies mental representations of images.

3

Gauthaman, Menard & Bonner, under review

Gauthaman, Menard & Bonner, in preparation

\text{cov}\left(X_\text{train}, Y_\text{train}\right) = U \Sigma V^\top

Learn latent dimensions

Step 1

Each is a linear combination of voxels

U_1, U_2, U_3, \dots
V_1, V_2, V_3, \dots

voxel 1

voxel 4

voxel N

...

U_{k,1}
U_{k,4}
U_{k,N}

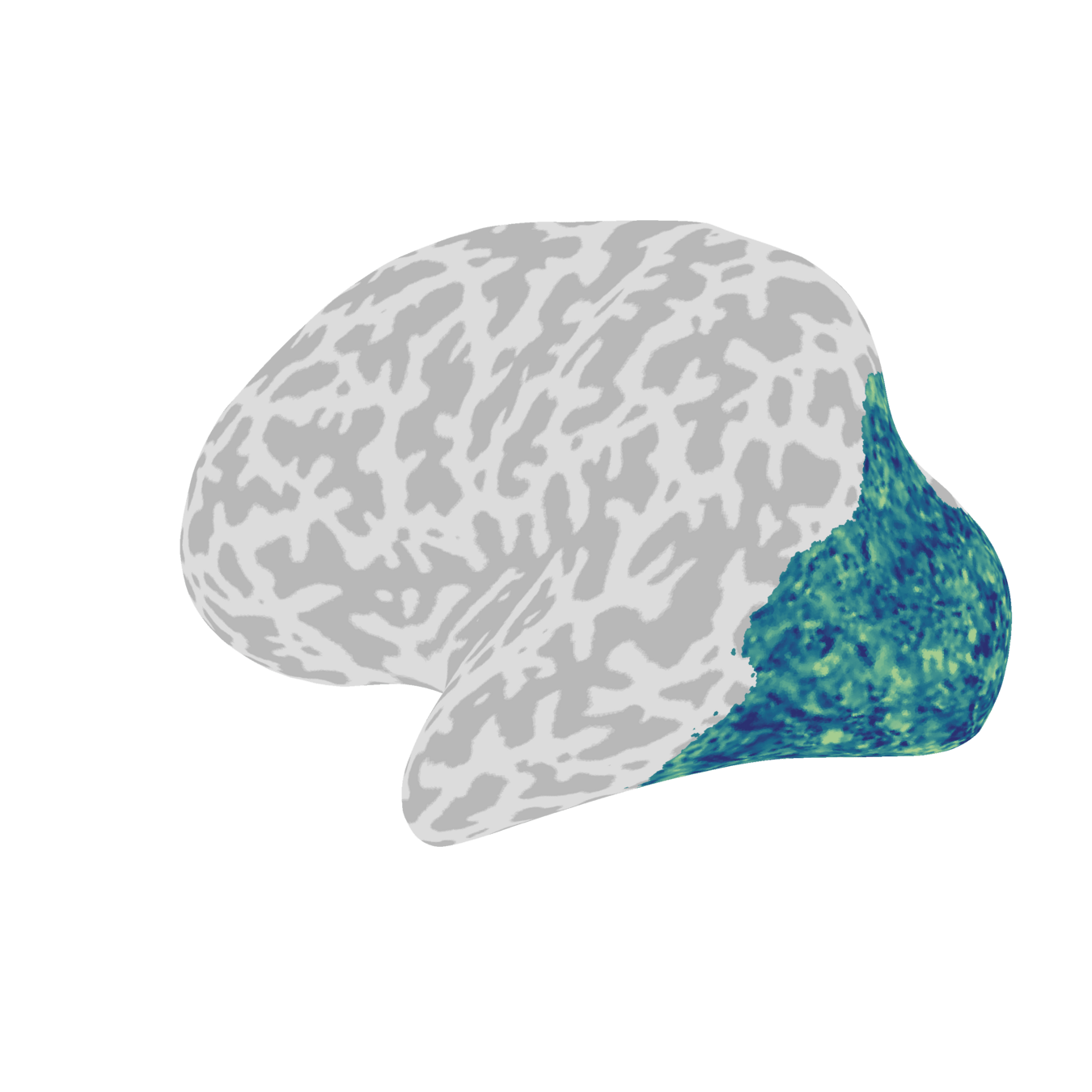
Latent dimensions are spatially distributed on cortex.

low-rank

high-rank

1

10

100

1,000

large spatial scale

small spatial scale

Latent dimensions are spatially distributed on cortex.

They show a rank-dependent spatial pattern.

1

30 mm

Latent dimensions are spatially distributed on cortex.

We can measure the characteristic spatial scale of each latent dimension.

human

mouse

10,000 neurons

primary visual cortex (V1)

Variance is distributed consistently over spatial scales.

human

mouse

\text{covariance} \propto \left(\text{spatial scale}\right)^\gamma

Most variance in the data is on large spatial scales.

1-D Fourier basis

2-D Fourier basis

Reminiscent of a Fourier basis ...

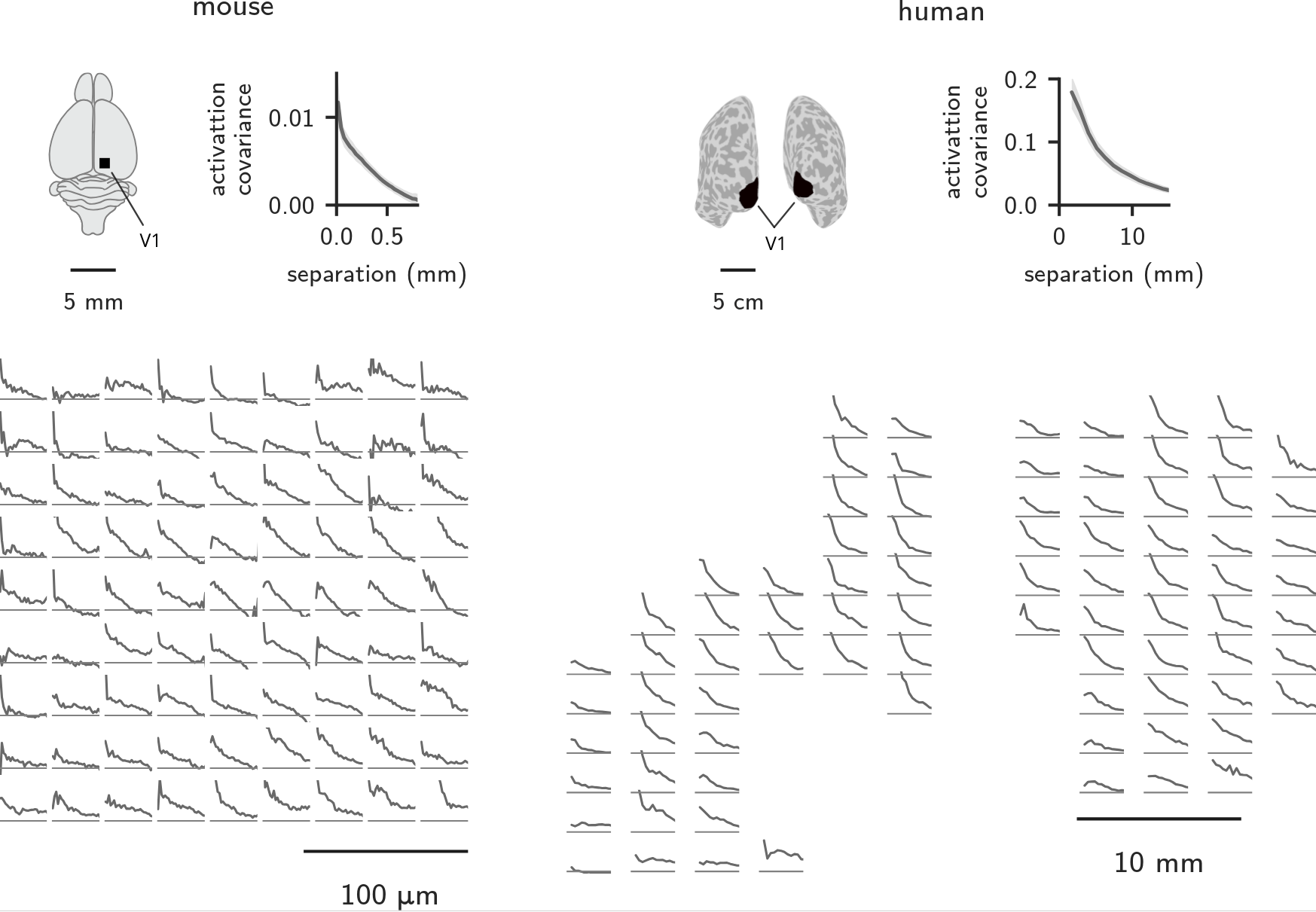
V1 correlation functions are ~translationally invariant

Answer: when data are translationally invariant

When do latent dimensions look like a Fourier basis?

number of neurons in human V1

spacing between neurons

a code that leverages all latent dimensions

Spatial scale: a potential organizing principle?

  • Most variance in the data is on large spatial scales, in both humans and mice
  • Even low-resolution imaging should capture most of the variance in the data

Coarse-graining should preserve covariance spectra.

spatial binning

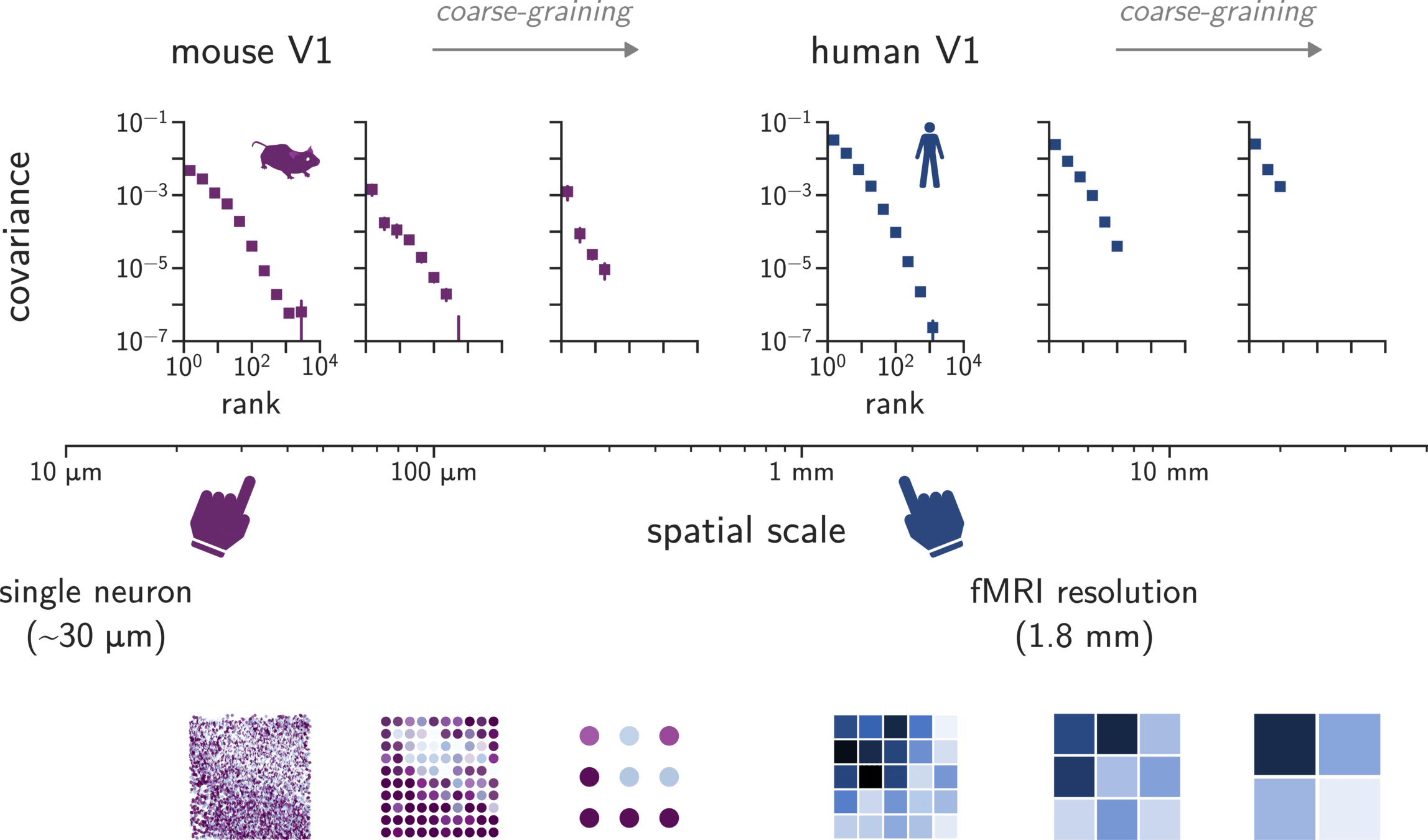
high-resolution data

simulated low-resolution data

V1 is self-similar over a wide range of spatial scales.

2

High-resolution neuroimaging probes low-variance dimensions

Invariance to spatial scale explains similar findings across fields

Outline of today's talk

Visual cortex representations are high-dimensional.

1

They are self-similar over a huge range of spatial scales.

2

The same geometry underlies mental representations of images.

3

Gauthaman, Menard & Bonner, under review

Gauthaman, Menard & Bonner, in preparation

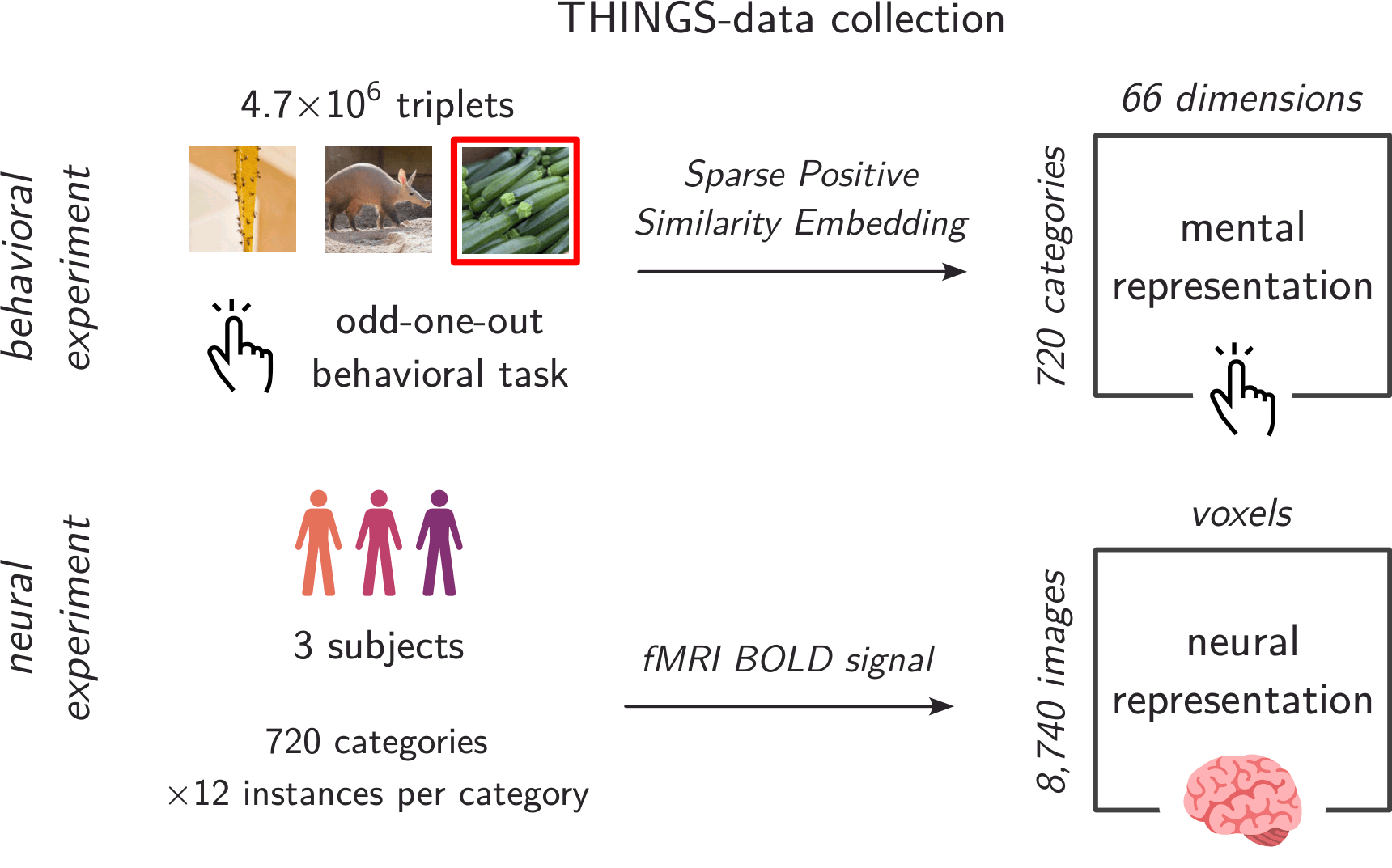
The THINGS initiative: same stimuli, many datasets

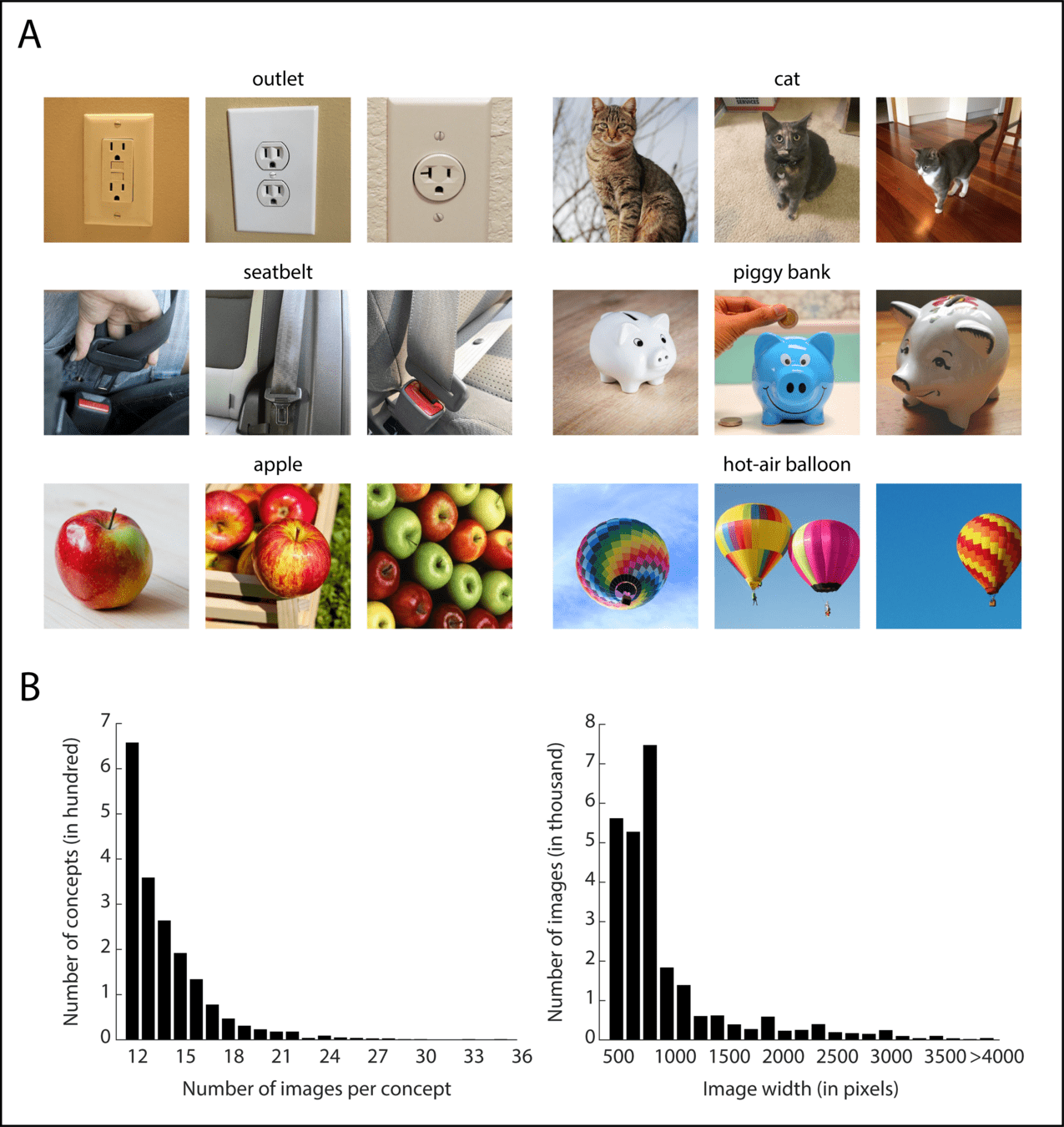
~26,000 images

1,854 categories

 

nameable, picturable nouns

The THINGS database has many diverse object categories.

What is the dimensionality of these neural representations of objects?

A large-scale fMRI dataset was collected on these objects.

Objects also evoke high-dimensional representations!

We replicate our earlier findings in the Natural Scenes Dataset.

10 0 10 3 10 −9 10 −7 10 −5 neural covariance V1 10 0 10 3 V2 10 0 10 3 V3 10 0 10 3 hV4 10 0 10 3 LOC 10 −3 rank

increasingly abstract object representations

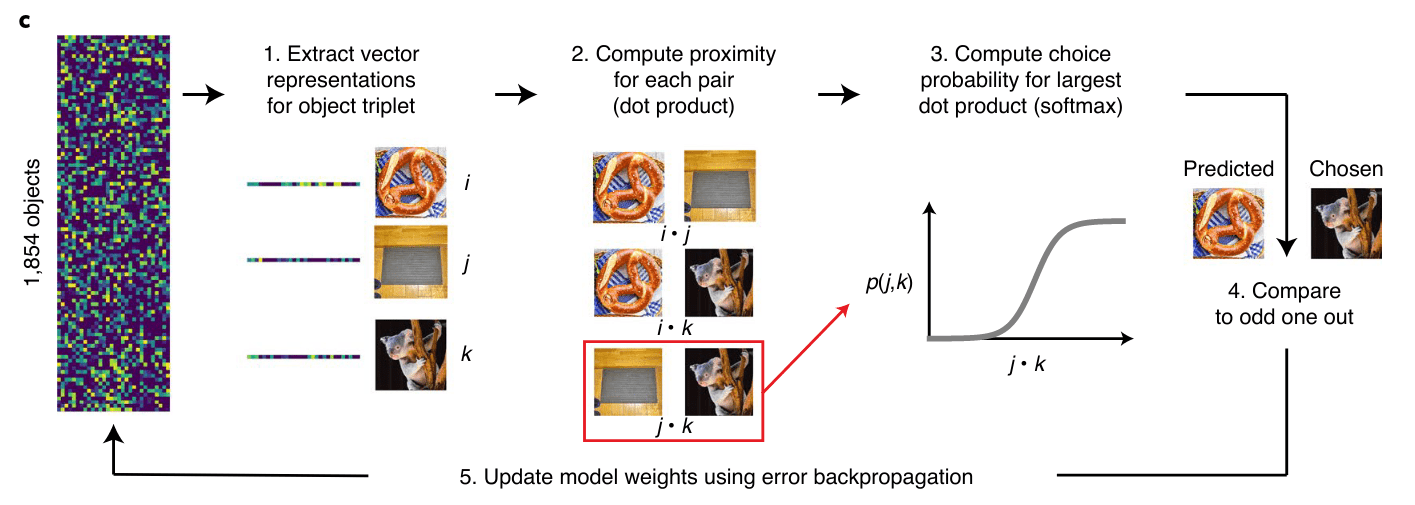
Which is the odd-one-out?

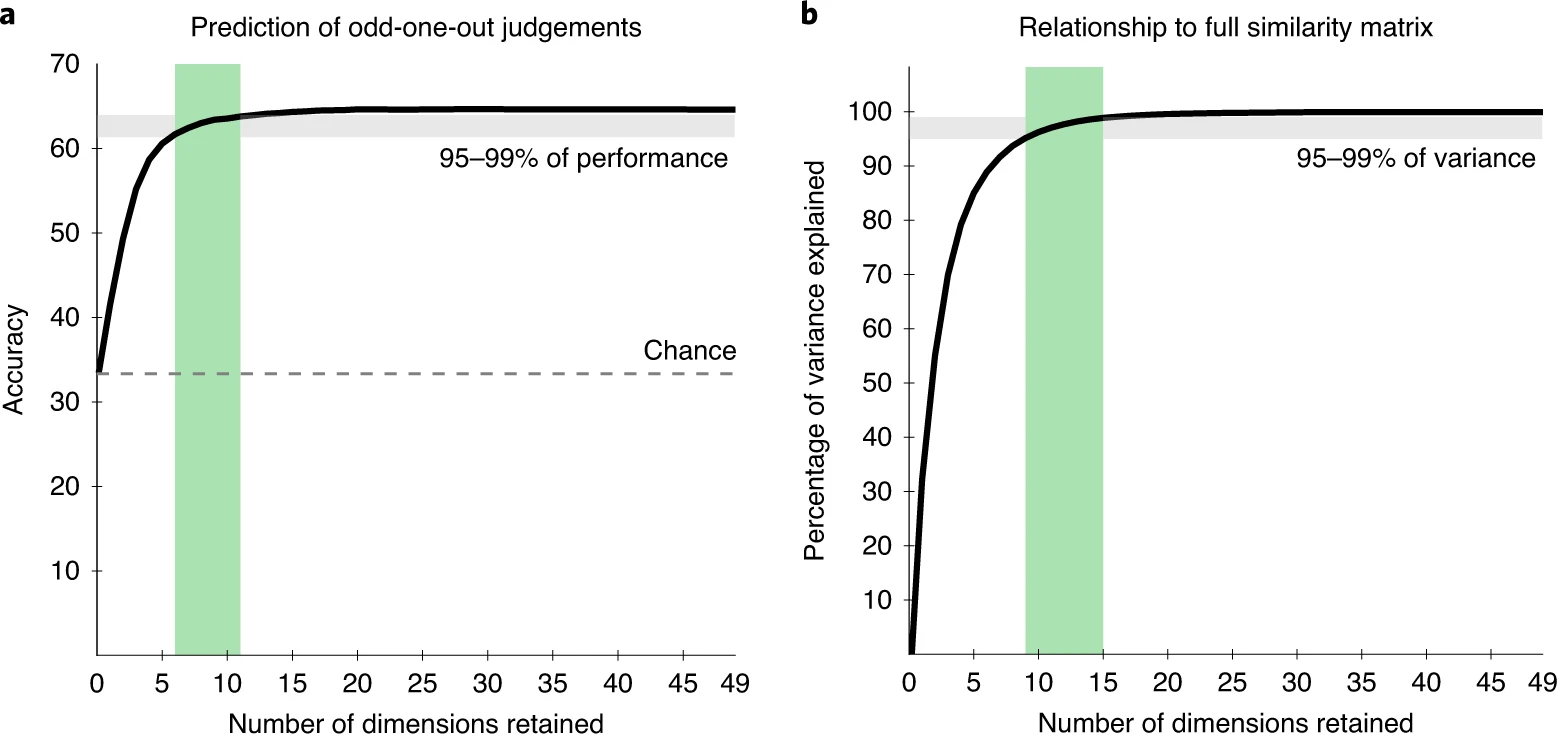
Large-scale similarity judgments were also collected.

Large-scale similarity judgments were also collected.

... and used to learn an embedding capturing the mental representations
that participants use when performing the odd-one-out task

Sparse Positive Similarity Embedding

Hebart et al. (2020)

Mental representations appear low-dimensional.

What is the underlying structure of these mental representations?

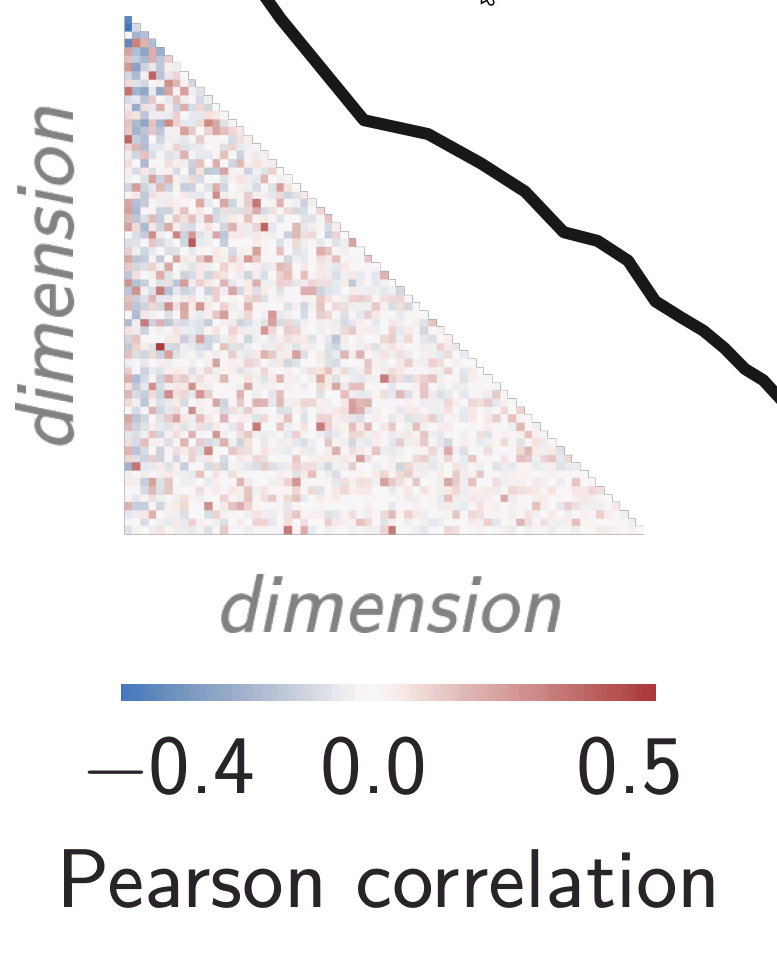
Covariance decays as a power-law

Latent dimensions have significant correlations

Mental representations have a power-law spectrum too!

There are power-law spectra in both cortical and behavioral data, but are they the same underlying representation?

How are neural and mental representations related?

generalizes

... to novel images

... across experiments

X_\text{train}
Y_\text{train}

mental

neural

neurons (or) voxels

stimuli

\text{cov}\left(X_\text{train}, Y_\text{train}\right) = U \Sigma V^\top

Learn latent dimensions

Step 1

Step 2

Evaluate reliable variance

\hat{\Sigma} = \text{cov}\left(X_\text{test} U, Y_\text{test} V\right)
X_\text{test}
Y_\text{test}

Cross-decomposition still works!

Systematic increase in shared dimensionality between neural and mental representations!

How are neural and mental representations related?

increasingly abstract object representations

Only 66 dimensions of mental representations were detected.

Why are mental representations so low-dimensional?

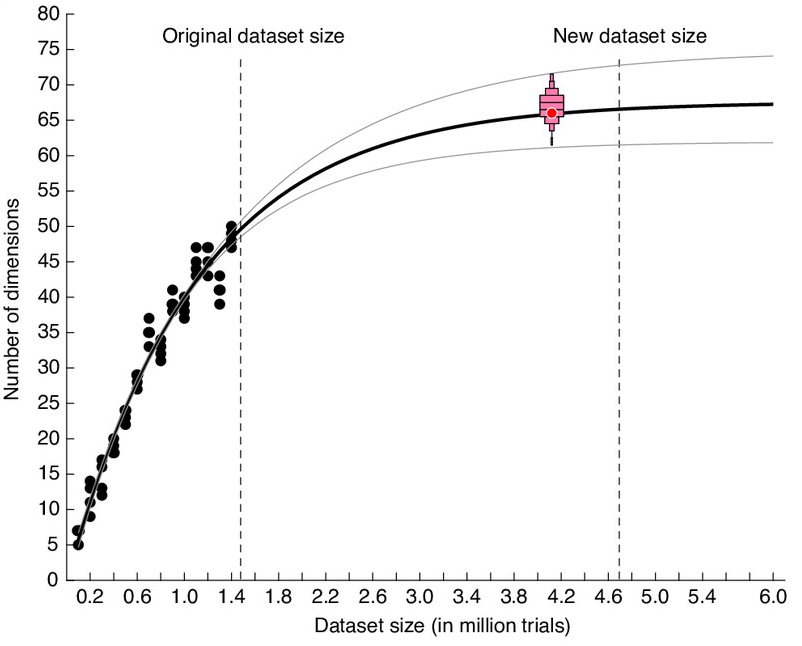
Scaling up the dataset doesn't help much!

49-D to 66-D

A potential cause: task complexity?

Why are mental representations so low-dimensional?

between-category triplets

(only coarse distinctions required)

within-category triplets

(fine distinctions required)

also has power-law covariance structure

Can we increase dimensionality using harder triplets?

coarse distinctions

fine distinctions

VGG-16 deep neural network

Simonyan & Zisserman (2015)

Can we increase dimensionality using harder triplets?

?

DNN

Yes, object representations increase in dimensionality when a DNN is forced to learn a more difficult task.

Can we increase dimensionality using harder triplets?

Visual cortex representations are high-dimensional.

1

They are self-similar over a huge range of spatial scales.

2

The same geometry underlies mental representations of images.

3

power-law covariance spectra

shared across subjects

remarkably similar across species

invariant to spatial scale

shared neural and mental representations

higher ranks encode finer distinctions

Thank you!

Brice Ménard

Michael F. Bonner

The Bonner Lab

The Isik Lab

The research presented in this dissertation was supported in part by a

  • Johns Hopkins Catalyst Award to Michael F. Bonner,
  • Institute for Data Intensive Engineering and Science Seed Funding to Michael F. Bonner and Brice Ménard, and
  • grant NSF PHY-2309135 to the Kavli Institute for Theoretical Physics.

“Thank you for paying us to do
what we would gladly pay to do.”
 

– S P Arun, Vision Lab, Indian Institute of Science

Discussion

Emerging evidence supports a high-dimensional view.

across species, in systems neuroscience

Wang et al. (2025)

zebrafish

Kong et al. (2022)

macaque

Stringer et al. (2019)

mouse

Agrawal et al. (2022)

Kong et al. (2022)

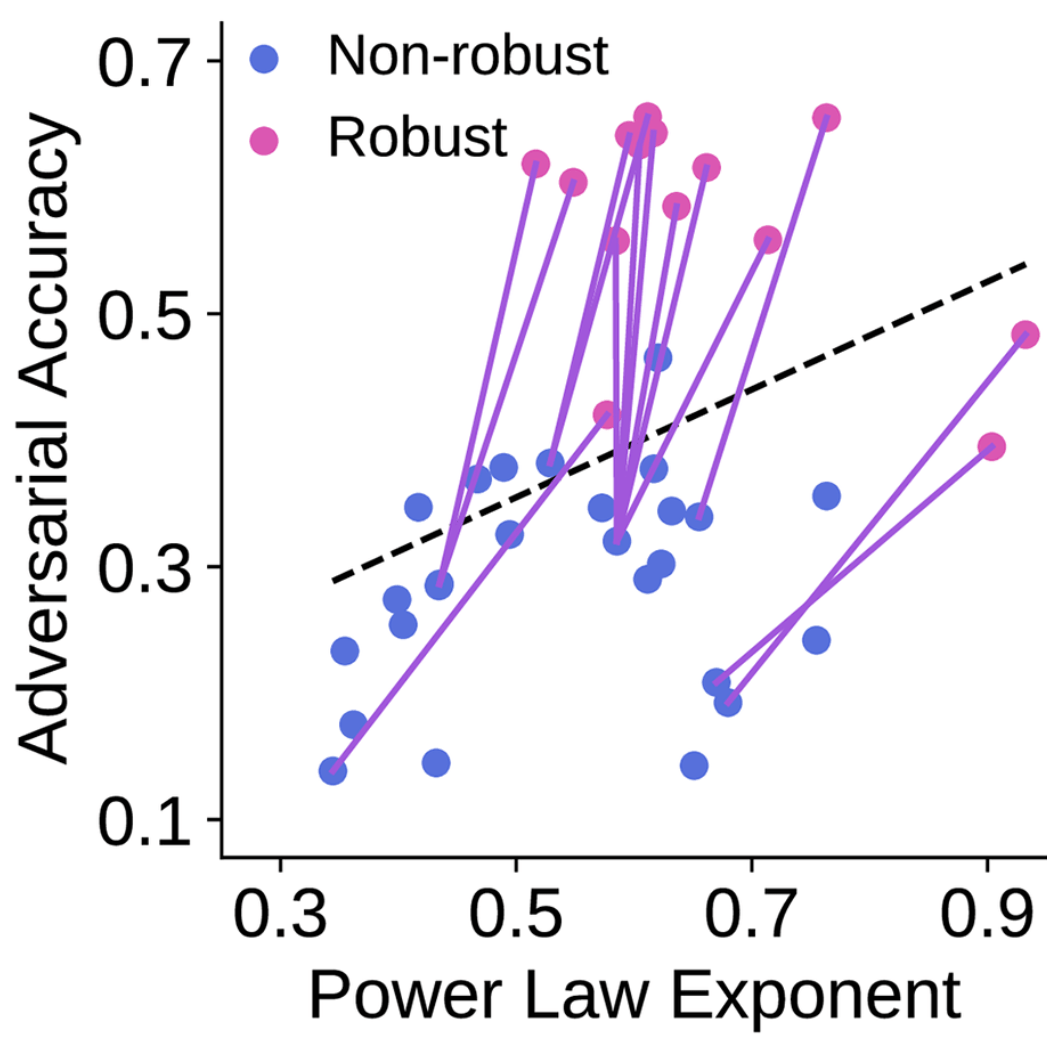
artificial neural networks

Emerging evidence supports a high-dimensional view.

out-of-distribution classification accuracy

adversarial robustness

Rigotti et al. (2013)

Emerging evidence supports a high-dimensional view.

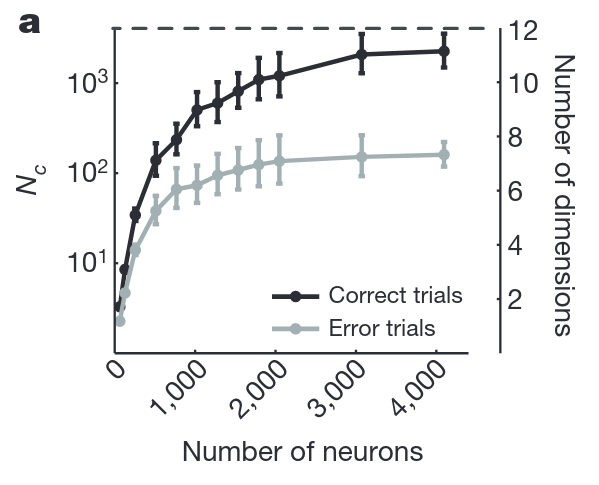
outside the visual system

prefrontal cortex

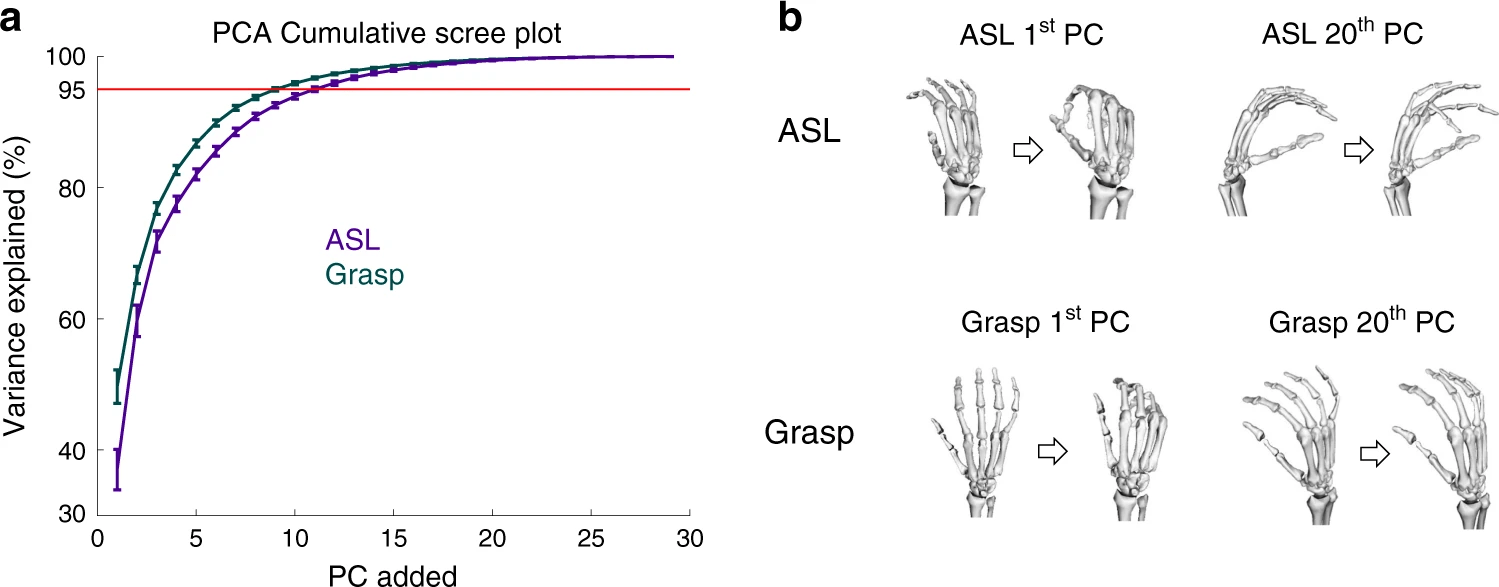
hand kinematics

Yan et al. (2020)

Catalog all the latent dimensions!

Understand the generative mechanisms!

Not helpful to interpret every latent dimension

Cognitive visual neuroscience needs new approaches.

We want theory!

Cognitive visual neuroscience needs new approaches.

X_\text{train}
Y_\text{train}

trial 1

trial 2

neurons (or) voxels

stimuli

X_\text{test}
Y_\text{test}

Limitations of cross-decomposition:

  • linear view of the system
  • second-order (Gaussian) description
  • not informative about visual features

We need new tools:

  • nonlinear dimensionality metrics
  • information-theoretic metrics
  • ???

Standard methods are insensitive to high-dimensional structure.

Potential future directions

More variety in

  • species
  • neuroimaging techniques
  • subject populations

For example,

  • Are kids' representations more low-dimensional?
  • What about patients with visual agnosia?

Potential future directions

  • Are there systematic variations across regions of the brain?
  • Does this generalize to other sensory or cognitive systems?

Potential future directions

also has power-law covariance structure

Simonyan & Zisserman (2015)

Using artificial vision systems to study the role of dimensionality, especially with causal manipulations

deep neural network

Potential future directions

How are other scale-free aspects of cortex
 

  • spatial organization
  • temporal signals
  • connectivity patterns

 

related to the scale-free representations we find here?

Chihye (Kelsey) Han

Are humans behaviorally sensitive to low-variance visual information present in the tail of the spectrum?

Individual differences in vision are high-dimensional.

FAQs

How much information about the stimulus can be encoded?

  • animate vs inanimate
  • stubby/boxy vs thin/elongated

How stable is the representation to irrelevant perturbations?

  • invariant recognition
  • smoothness of the code

low-D

high-D

Why is dimensionality a useful measure?

robustness

expressivity

Power-law index* of −1: a critical point

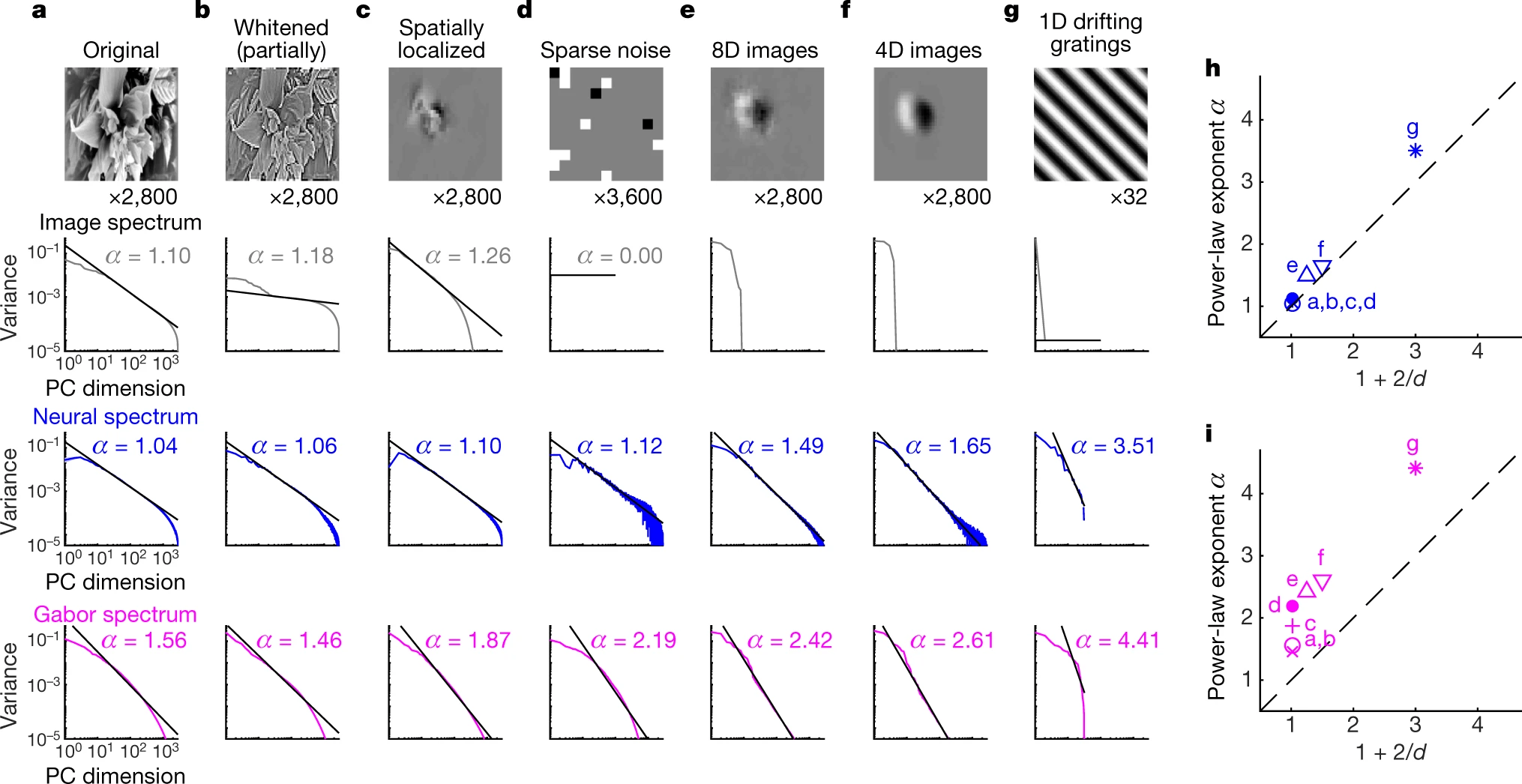
Is the power law simply due to stimulus statistics?

Zipf's law: the classic power law

\text{word frequency} \propto \left(\text{rank}\right)^{-1}

Why should we care about low-variance dimensions?

i love sci-fi and am willing to put up with a lot. Sci-fi movies/tv are usually underfunded, under-appreciated and misunderstood. I tried to like this, I really did, but it is to good tv sci-fi as babylon 5 is to star trek (the original). Silly prosthetics, cheap cardboard sets, stilted dialogues, cg that doesn't match the background, and painfully one-dimensional characters cannot be overcome with a'sci-fi'setting. (I'm sure there are those of you out there who think babylon 5 is good sci-fi tv. It's not. It's clichéd and uninspiring.) while us viewers might like emotion and character development, sci-fi is a genre that does not take itself seriously (cf. Star trek). [...]

i love and to up with a lot. Are, and. I to like this, I really did, but it is to good as is to (the).,,, that doesn't the, and characters be with a''. (I'm there are those of you out there who think is good. It's not. It's and.) while us like and character, is a that does not take [...]

Using only the 200 most frequent words...

What are these latent dimensions encoding?

Ramesh et al. (2022)

Where can I learn more about this fascinating stuff? ;)

Made with Slides.com