To transform or not to transform?

Rebecca Barter

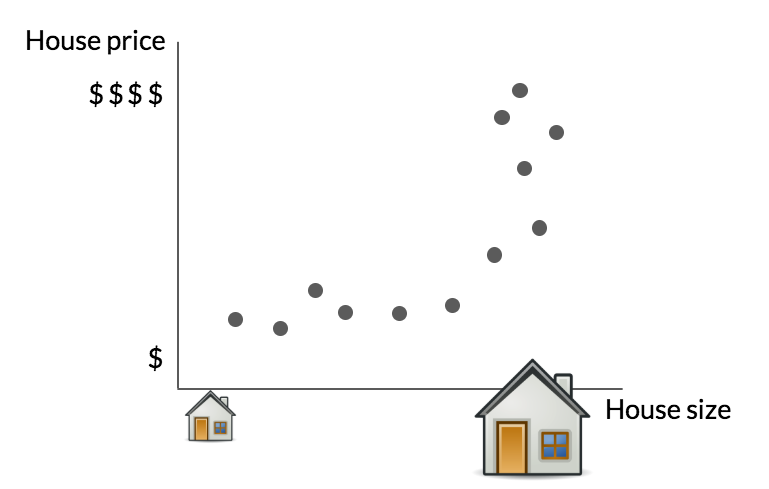
Some context...

House price

$

$

House size

$

$

$

\textrm{House price} = \alpha + \beta \textrm{House size} + \epsilon
House price=α+βHouse size+ϵ\textrm{House price} = \alpha + \beta \textrm{House size} + \epsilon

Some context...

House price

$

$

House size

$

$

$

\textrm{House price} = \alpha + \beta \textrm{House size} + \epsilon
House price=α+βHouse size+ϵ\textrm{House price} = \alpha + \beta \textrm{House size} + \epsilon

Some context...

House price

$

$

log(House size)

$

$

$

log(           )

log

(     )

\textrm{House price} = \alpha + \beta \log(\textrm{House size}) + \epsilon
House price=α+βlog⁡(House size)+ϵ\textrm{House price} = \alpha + \beta \log(\textrm{House size}) + \epsilon

When do people usually transform their variables?

Poor model accuracy

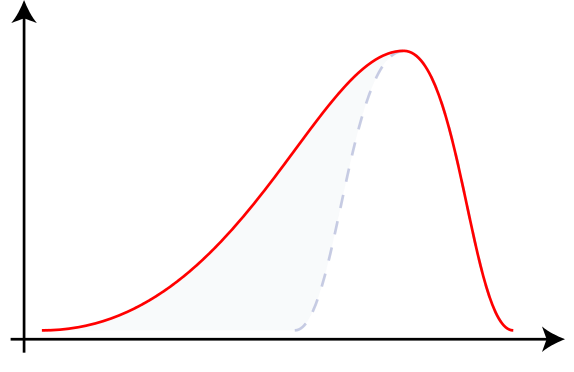
Variables are not normal

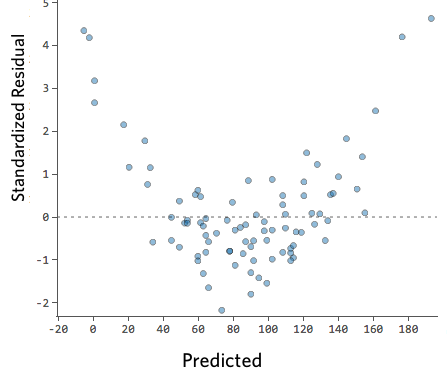
Weird looking residual plot

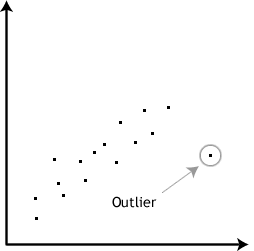
Outliers are present

Relationship doesn't look linear

indicates your model assumptions are wrong

(if you care about inference)

If you can predict better with transformed variables, great!

(if you care about pred. accuracy)

Common misconception:

Variables in a regression don't actually need to be normal

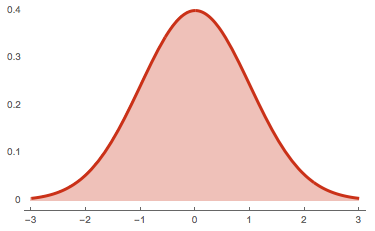
...but the "errors" do!*

*Actually... we don't even need the errors to be normal.
They just need to be independent, have zero mean and common variance

Common transformations:

the logarithm

Interpreting log transforms:

 increasing

Drawbacks:

can't be used for values 

What it does:

compresses large vales and spreads small values

\beta
β\beta
Y \sim X:
Y∼X:Y \sim X:

by

increases

by

X
XX
1
11
Y
YY
\log(Y) \sim \log(X):
log⁡(Y)∼log⁡(X):\log(Y) \sim \log(X):

multiplying

e^\beta
eβe^\beta

by

multiplies

by

X
XX
Y
YY
e
ee
Y \sim \log(X):
Y∼log⁡(X):Y \sim \log(X):

multiplying 

\beta
β\beta

by

increases

by

X
XX
Y
YY
e
ee
\log(Y) \sim X:
log⁡(Y)∼X:\log(Y) \sim X:

 increasing

e^\beta
eβe^\beta

by

multiplies

by

X
XX
Y
YY
\textrm{1}
1\textrm{1}
\leq 0
≤0\leq 0

Common transformations:

the square-root

Interpreting log transforms:

 increasing

Drawbacks:

can't be used for values 

What it does:

compresses large vales and spreads small values

Y \sim X:
Y∼X:Y \sim X:

by

increases

by

X
XX
1
11
Y
YY
\sqrt{Y} \sim \sqrt{X}:
Y∼X:\sqrt{Y} \sim \sqrt{X}:

 increasing

by

increases

by

X
XX
Y
YY
1
11
Y \sim \sqrt{X}:
Y∼X:Y \sim \sqrt{X}:

 increasing

by

increases

by

X
XX
Y
YY
1
11
\sqrt{Y} \sim X:
Y∼X:\sqrt{Y} \sim X:

 increasing

by

increases

by

X
XX
Y
YY
1
11
< 0
&lt;0&lt; 0
\beta
β\beta
?
??
?
??
?
??

Common course of action

Run regression on the raw data

Compute R2

Transform variables because you think you can do better

Re-run regression with transformed variables

Re-compute R2

Repeat

Consequences of transformation

Incorrectly interpreting model coefficients

Multiple testing problems

To transform or not to transform?

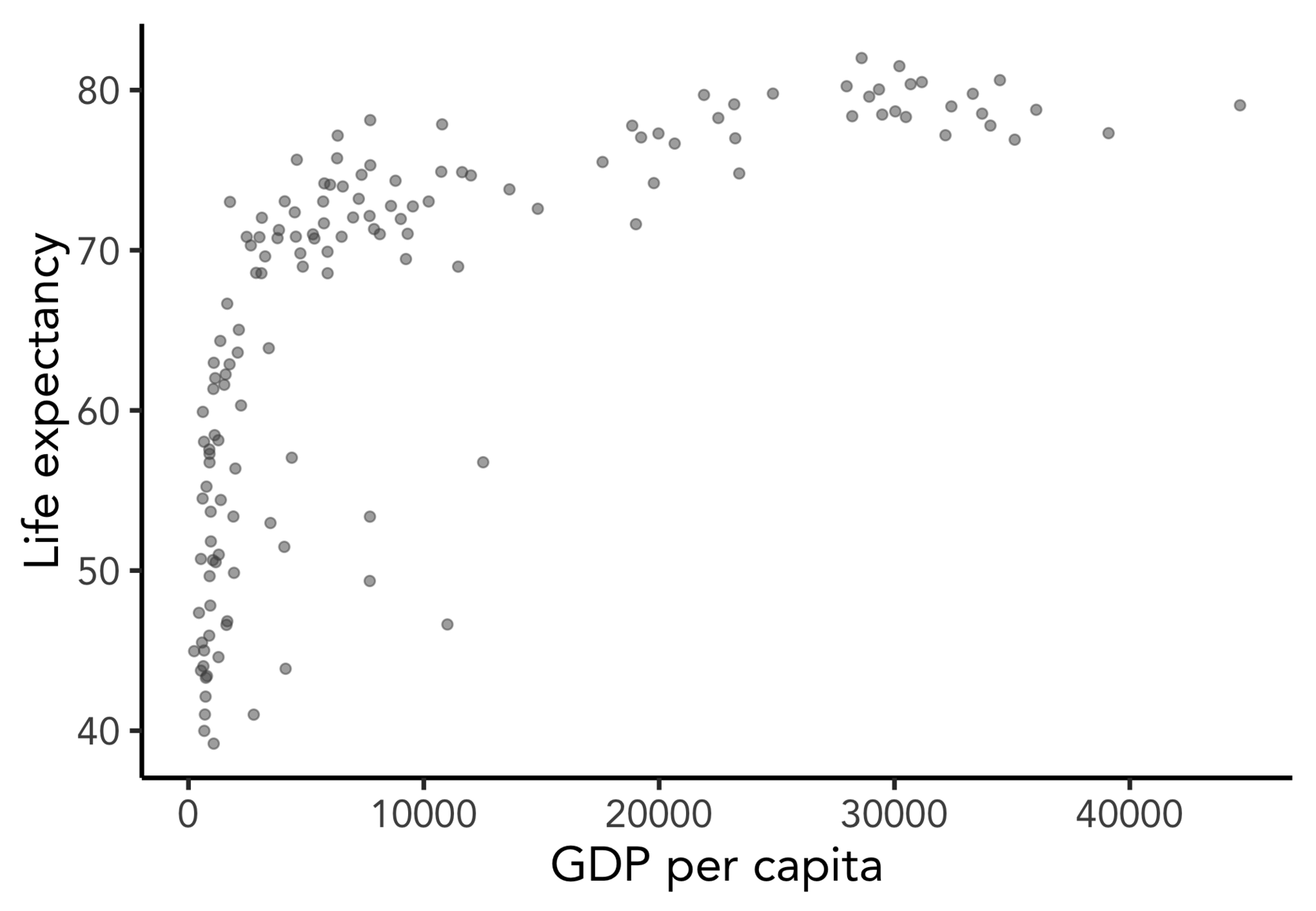
Goal: predict life expectancy based on GDP per capita

\widehat{\textrm{Life expectancy}} = 54.0 + 0.000765 \times(\textrm{GDP per cap} )
Life expectancy^=54.0+0.000765×(GDP per cap)\widehat{\textrm{Life expectancy}} = 54.0 + 0.000765 \times(\textrm{GDP per cap} )
R^2 = 0.34
R2=0.34R^2 = 0.34
\widehat{\textrm{Life expectancy}} = -9.1 + 8.4 \log(\textrm{GDP per cap} )
Life expectancy^=−9.1+8.4log⁡(GDP per cap)\widehat{\textrm{Life expectancy}} = -9.1 + 8.4 \log(\textrm{GDP per cap} )
R^2 = 0.65
R2=0.65R^2 = 0.65

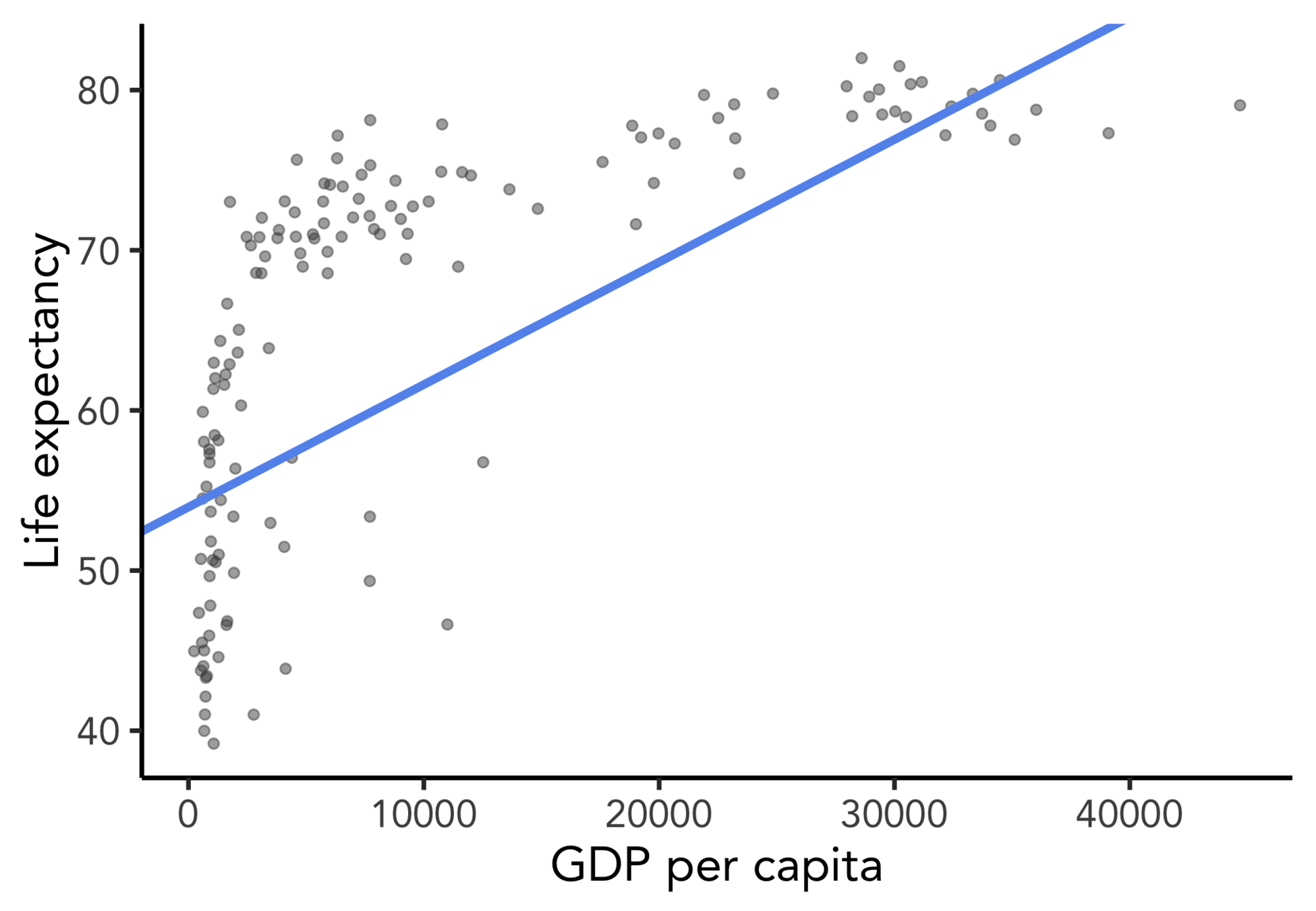
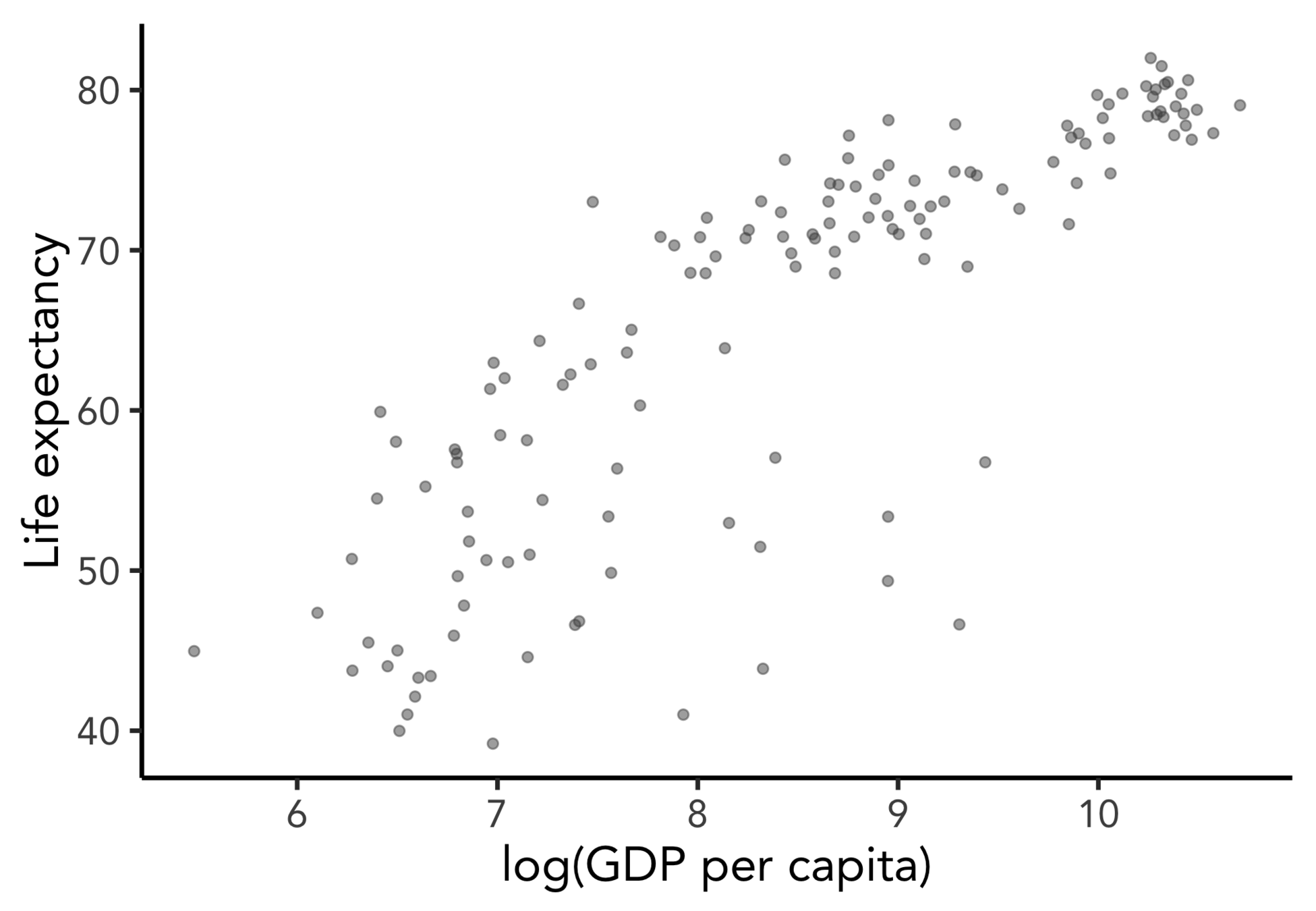
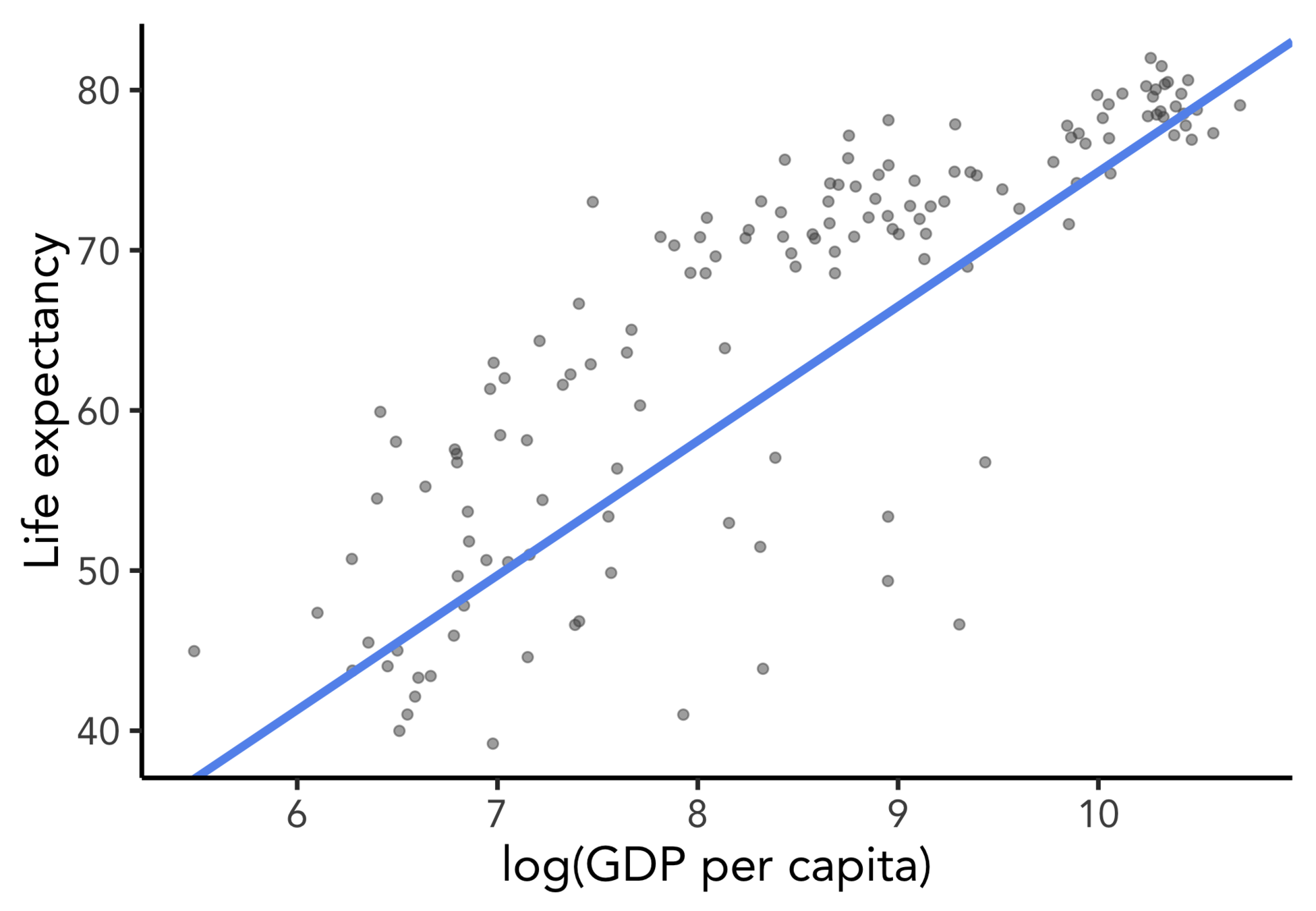
Goal: estimate effect of GDP on life expectancy

The bottom line is...

Made with Slides.com