Grafos
Usos de los grafos
Mapas y georeferenciación
Usos de los grafos
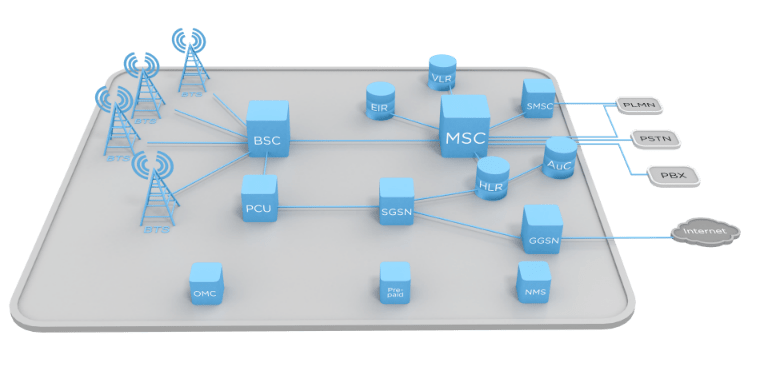
Telecomunicaciones
Usos de los grafos
Astronomía
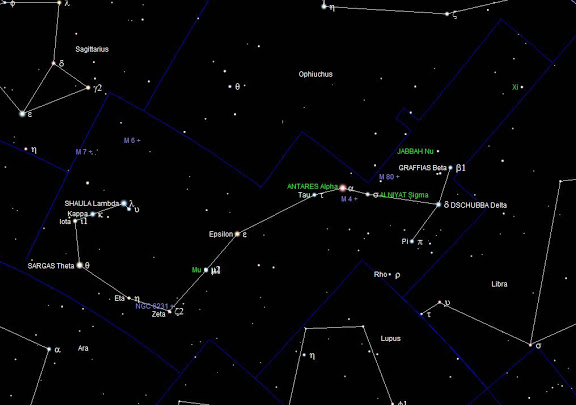
Usos de los grafos
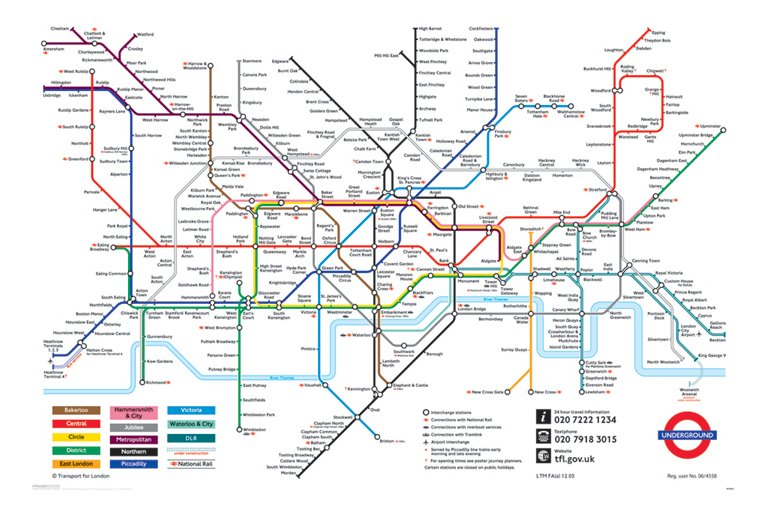
Metro de Londres
Usos de los grafos
Metro
de
Moscú
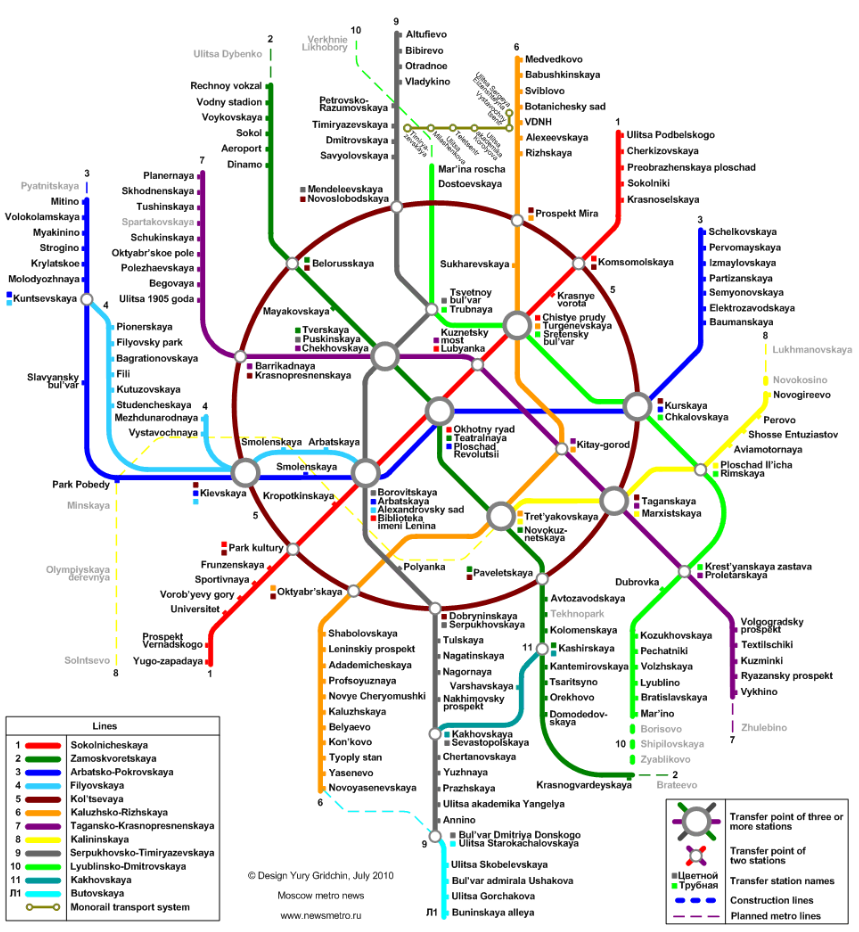
Usos de los grafos
Planeación de rutas de transporte público
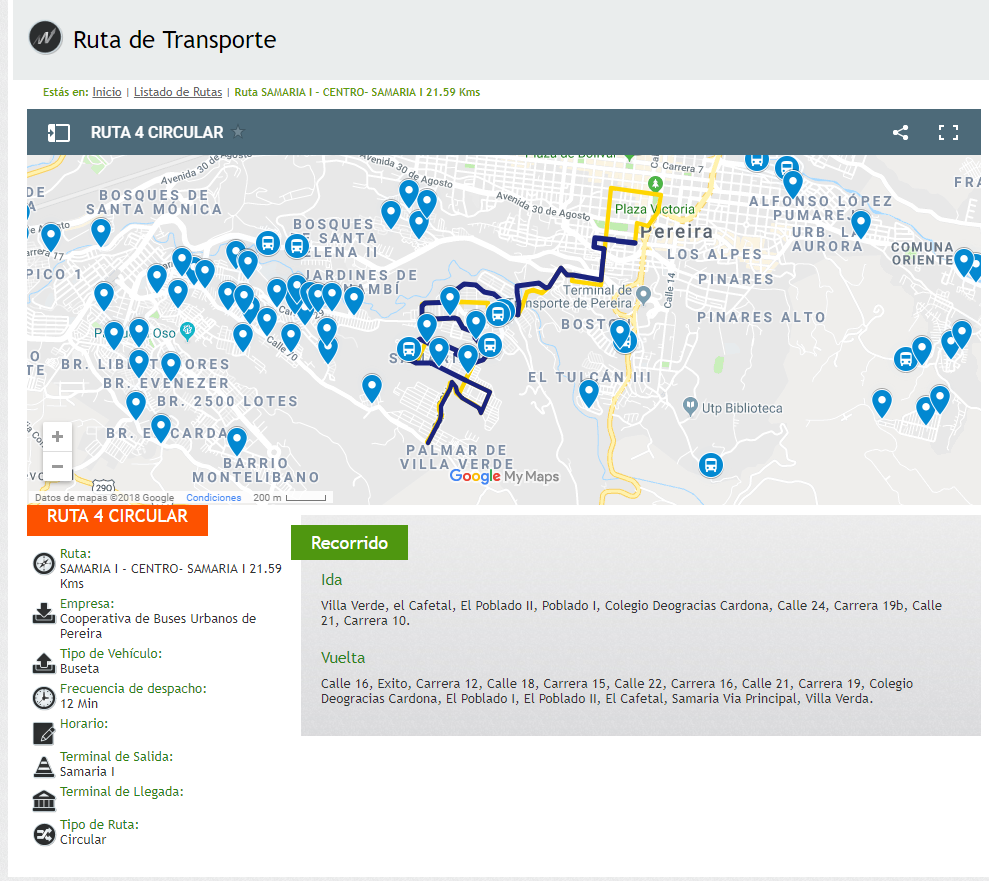
Grafos
Quimica
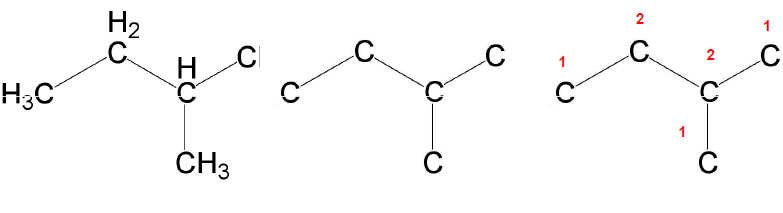
Ejemplos
Grafos
Conceptos y definiciones
Definición
Agrupación de entes físicos o conceptuales y relaciones entre ellos.
Grafo (Graph/Network)
G = (V, A)
V = Conjunto de Vértices
A = Conjunto de Aristas
Representación
VERTICE A
VERTICE B
ARISTA
Pereira
Medellín
Definición
Es la representación de un elemento físico o conceptual.
Vértice
- Ciudades
- Números
- Personas
- Moléculas

G = (V,A)
V = {pereira, cali, Medellín}
Definición
Representa una relación entre dos nodos.
Arco / Arista (Arc / Edge)
- Dirigidos
G = (V,A)
A = {(pereira, cali), (Pereira,Medellín)}
VERTICE A
VERTICE B
Pereira
Medellín
VERTICE A
VERTICE B
Pereira
Medellín
- No Dirigidos
Tipos de grafo
- Dirigidos
- No dirigidos
- Grafo con pesos
VERTICE A
VERTICE B
Pereira
Medellín
VERTICE A
VERTICE B
Pereira
Medellín
VERTICE A
VERTICE B
Pereira
Medellín
380 Km
Grafo simple
Sin bucles ni arcos paralelos
Grafo plano
Los arcos no se pueden cruzar
Grafo lineal
Se puede expresar como una línea
Grafo Cn (Rueda)
Los arcos forman un ciclo completo
Grafo Kn
Todos sus vertices se conectan entre si
Grafo Km, n
Dos grupos que se conectan entre ellos, pero no con elementos del mismo grupo
Componentes conexas
Grafo conexo: Existe un camino entre cualquier par de vértices que forman el grafo.
Para saber si un grafo es conexo o no se hace un recorrido del mismo.
1. Realizar un recorrido del grafo a partir de cualquier vértice w.
2. Si en el recorrido se han marcado todos los vértices, entonces el grafo es conexo.
3. Si el grafo no es conexo, los vértices marcados forman una componente conexa.
4. Se toma un vértice no marcado, z, y se realiza de nuevo el recorrido del grafo a partir de z. Los nuevo vértices marcados forman otra componente conexa.
5. El algoritmo termina cuando todos los vértices han sido marcados (visitados)
Componentes fuertemente conexas
Un grafo dirigido fuertemente conexo es aquel en el cual existe un camino entre cualquier par
de vértices del grafo.
De no ser fuertemente conexo se pueden determinar componentes fuertemente conexas (Se puede usar el algoritmo de recorrido en profundidad para identificarlas)
a
d
e
c
b
Grafo dirigido
a
d
e
c
b
Componentes fuertes
Grafos
Tipo abstracto de dato (T.A.D.)
Creando el TAD
A
B
C
D
E
Creando el TAD
A
B
C
D
E
VERTICES
Creando el TAD
A
B
C
D
E
ARCOS
EJEMPLO: (A,C)
TAD: CON MATRIZ DE ADYACENCIA
VERTICE
GRAFO
| A | B | |
|---|---|---|
| A | 0 | 50 |
| B | 50 | 0 |
MATRIZ DE ADYACENCIA
String dato
Vertice[] vertices
int[][] matrizAdyacencia
TAD: CON LISTA DE ADYACENCIA
VERTICE
GRAFO
String dato
Vertice[] vertices
List<Arco> listaAdyacencia
ARCO
Vértice origen
Vértice destino
VENTAJAS DE LISTA FRENTE A MATRIZ
- Incrementar la cantidad de vértices, sin tener que ejecutar algoritmos complejos (Memoria dinámica)
Integer peso
Grafos
Implementación
Grafos
Algoritmos comunes de grafos
Pseudocódigo
Recorrido en profundidad
DFS (Deep First Search)
- Permite recorrer todos los vértices de un grafo.
- Funciona como el recorrido de preorden de en árboles.
- Parte de un vértice y visita sus vértices adyacentes uno a uno, cuando exista un vértice sin adyacentes se retorna de manera recursiva al vértice inmediatamente anterior.
- Si existen vértices no alcanzables desde el vértice de partida, se procede a seleccionar otro vértice de partida. (Recorrido incompleto)
DFS (Deep First Search)
- Marcar todos los vértices como no visitados
- Elegir un vértice como punto de partida.
- Marcar el vértice como visitado
- Recorrer todos los vertices adyacentes al vértice inicial, si el sub vértice no ha sido visitado llamar recursivamente para ejecutar 3 y 4.
Inicializar marca
Para todos los vértices no marcados llamar a DFS
DFS: Para cada sub vértice si este no es visitado llamar a DFS
Aplicaciones
Recorrido en profundidad
- Encontrar componentes conexas de un grafo no dirigido.
- Revisar si un grafo tiene o no ciclos
- Encontrar componentes fuertemente conexas
Recorrido en Amplitud
BFS - Breadth First Search
Supone recorrer el grafo por niveles parecidos a los de un arbol. Es decir, primero se recorren los que esten a un paso del vertice origen, luego los que están a dos pasos, luego a tres y así sucesivamente hasta que estén marcados todos los vertices del grafo.
Se puede usar una estructura de datos COLA.
- Se encola el vertice actual.
- Se atiende el vertice actual y se encolan los vertices adyacentes.
- Se hace 1 y 2 hasta que no se tengan vertices adyacentes.
Aplicaciones
- Para explorar segmentos de un grafo finito o de grandes dimensiones.
- Para encontrar el camino más corto
- Para encontrar la solución a un problema usando el menor número de pasos posibles