Functional JavaScript

Rob Hilgefort

> whoami

Background

Rob Hilgefort
Cincinnati, OH native
University of Kentucky graduate
Moved to Denver, CO in 2018
10 years professional JS experience

Contact

: rjhilgefort
: rjhilgefort
: rob.hilgefort.me

This Is

A Zero FP knowledge talk
Enablement to read/write FP in the real world

This Is Not

An intro to JS
A deep dive into FP
ADT Coverage
A Hindley Milner Notation Intro (probably)

At A Glance

(let's look at some code)

Imperative Approach

const users = [
  { active: true, first: 'Rob   ', last: '   Hilgefort ' }, // 12
  { active: true, first: 'John  ', last: ' Doe' }, // 7
  { active: false, first: '  Jane', last: 'Smith   ' },  // 9
  { active: true, first: 'Jesselin  ', last: ' Alexandra ' }, // 17
]

const sumNameLengths = (users) => {
  let filteredUsers = []
  for (let i = 0; i < users.length; i++) {
    const user = users[i]
    if (user.active) {
      filteredUsers.push(user)
    }
  }
  
  let allLengths = 0
  for (let i = 0; i < filteredUsers.length; i++) {
    const user = filteredUsers[i]
    allLengths += user.first.trim().length + user.last.trim().length
  }  
  
  return allLengths
}

sumNameLengths(users) // 36

Problems With Imperative

const users = [
  { active: true, first: 'Rob   ', last: '   Hilgefort ' }, // 12
  { active: true, first: 'John  ', last: ' Doe' }, // 7
  { active: false, first: '  Jane', last: 'Smith   ' },  // 9
  { active: true, first: 'Jesselin  ', last: ' Alexandra ' }, // 17
]

const sumNameLengths = (users) => {
  let filteredUsers = [] // intermediate state
  for (let i = 0; i < users.length; i++) { // Duplicate structure traversal code
    const user = users[i] // intermediate state
    if (user.active) {
      filteredUsers.push(user)
    }
  }
  
  let allLengths = 0
  for (let i = 0; i < filteredUsers.length; i++) { // Duplicate structure traversal code
    const user = filteredUsers[i] // easy to make a mistake here and reference `users`
    // hard to see what the math is we're even doing
    allLengths += user.first.trim().length + user.last.trim().length
  }  
  
  return allLengths // Other variables don't matter and are just intermediate state
}

sumNameLengths(users)

Declarative / FP

import { pipe, filter, map, pipe, pick, trim, length, values, sum } from 'ramda'

const users = [
  { active: true, first: 'Rob   ', last: '   Hilgefort ' }, // 12
  { active: true, first: 'John  ', last: ' Doe' }, // 7
  { active: false, first: '  Jane', last: 'Smith   ' },  // 9
  { active: true, first: 'Jesselin  ', last: ' Alexandra ' }, // 17
]

// User :: { active: Bool, first: String, last: String }
// sumNameLength :: [User] -> Number
const sumNameLength = pipe(
  filter(propEq('active', true)),
  map(pipe(
    pick(['first', 'last']),
    map(pipe(trim, length)),
    values,
    sum,
  )),
  sum,
)

sumNameLength(users) // 36

Is that even JavaScript?

WAT

Learning Curve

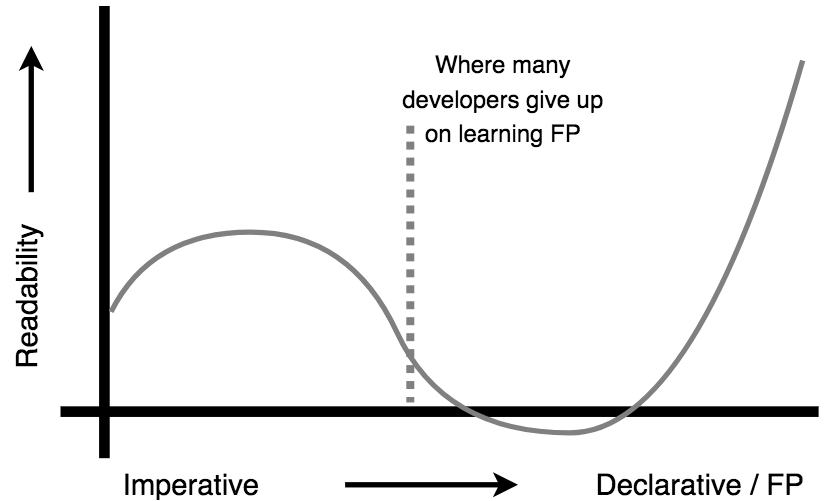
Functional Programming

Functional programming (FP) is a programming paradigm that is the process of building software by composing pure functions and avoiding shared state, mutable data, and side-effects.

Data passes through transformations.

vs Object Oriented Programming

This is different than Object oriented programming (OOP), where application state is usually shared and colocated with methods in objects.

Why Functional Programming?

Problems With Imperative


Error Prone	It's much easier to make mistakes when you have more code and more variables to keep track of
Hard To Refactor	The math we were doing was coupled with the structure traversal
Mutations	Easy to have unexpected side effects happen when mutating state
Noise	The data being acted on is buried in code that is extraneous
!Single Responsibility Principle:	Operations/Logic are coupled and harder to reuse

FP Advantages


Predictability	Pure functions mean we always get the same output for a given input
Testability	Pure functions are easy to test because you don't have to mock
Easy To Reason About	Declarative code indicates intent and desire, self documenting
Single Responsibility Principle	FP encourages tiny composable methods (lego blocks) which are easy to reuse
Refactorability	Tiny composable methods are easy to move around and/or remove

How?

1️⃣ Tools

Higher Order Functions
Currying
Composition

2️⃣ Rules

Purity
Immutability
No Side Effects

3️⃣ Concepts

Declarative
First Class Functions
Point Free

FP Topics

Don't Worry!

We'll cover these, look for this icon!

Let's Break This Down

import { pipe, filter, map, pipe, pick, trim, length, values, sum } from 'ramda'

const users = [
  { active: true, first: 'Rob   ', last: '   Hilgefort ' }, // 12
  { active: true, first: 'John  ', last: ' Doe' }, // 7
  { active: false, first: '  Jane', last: 'Smith   ' },  // 9
  { active: true, first: 'Jesselin  ', last: ' Alexandra ' }, // 17
]

// User :: { active: Bool, first: String, last: String }
// sumNameLength :: [User] -> Number
const sumNameLength = pipe(
  filter(propEq('active', true)),
  map(pipe(
    pick(['first', 'last']),
    map(pipe(trim, length)),
    values,
    sum,
  )),
  sum,
)

sumNameLength(users) // 36

Filtering The Users

import { pipe, filter, map, pipe, pick, trim, length, values, sum } from 'ramda'

const users = [
  { active: true, first: 'Rob   ', last: '   Hilgefort ' }, // 12
  { active: true, first: 'John  ', last: ' Doe' }, // 7
  { active: false, first: '  Jane', last: 'Smith   ' },  // 9
  { active: true, first: 'Jesselin  ', last: ' Alexandra ' }, // 17
]

// User :: { active: Bool, first: String, last: String }
// sumNameLength :: [User] -> Number
const sumNameLength = pipe(
  filter(
    propEq('active', true)
  ),
  map(pipe(
    pick(['first', 'last']),
    map(
      pipe(trim, length)
    ),
    values,
    sum,
  )),
  sum,
)

sumNameLength(users) // 36

In `sumNameLength`, we first need to select only the active users from the list. We need to filter the list.

Imperative Filter

const sumNameLengths = (users) => {
  let filteredUsers = []
  for (let i = 0; i < users.length; i++) {
    const user = users[i]
    if (user.active) {
      filteredUsers.push(user)
    }
  }
  
  let allLengths = 0
  for (let i = 0; i < filteredUsers.length; i++) {
    const user = filteredUsers[i]
    allLengths += user.first.trim().length + user.last.trim().length
  }  
  
  return allLengths
}

In our imperative approach, we described how to filter, and we tightly coupled our array traversal with our "predicate" (condition).

Furthermore, our function has to be concerned with how to traverse an array. Ideally, it would just say what it wants to filter on, and not be concerned with how.

Single Responsibility Principle

// filter :: 
//   ((* -> Boolean), Array a) 
//     -> Array b
const filter = (predicate, data) => {
  let filtered = []
  for (let i = 0; i < data.length; i++) {
    const val = data[i]
    if (predicate(val)) {
      filtered.push(val)
    }
  }
  return filtered
}

// isLessThan5 :: Number -> Boolean
const isLessThan5 = x => x < 5

filter(isLessThan5, [1, 3, 6, 8])
// -> [1, 3]

Let's hide all the details of how to traverse a list and filter by a predicate.

This allows us to reuse this functionality and allow the callers to say what they want, and not be concerned with how to do it.

FP Topics

1️⃣ Tools

Higher Order Functions
Currying
Composition

2️⃣ Rules

Purity
Immutability
No Side Effects

3️⃣ Concepts

Declarative
First Class Functions
Point Free

Declarative Programming

// Imperative
// Double every number in list

const nums = [2, 5, 8];

for (let i = 0; i < nums.length; i++) {
  nums[i] = nums[i] * 2
}

nums // [4, 10, 16]

Express the logic of a computation without describing its control flow.

Programming is done with expressions or declarations instead of statements. In contrast, imperative programming uses statements that change a program's state.

// Declarative
// Double every number in list

const double = x => x * 2

const nums = [2, 5, 8];
const numsDoubled = nums.map(double)

numsDoubled // [4, 10, 16]

First Class Functions

Functions are values.

First class function support means we can treat functions like any other data type and there is nothing particularly special about them - they may be stored in arrays, passed around as function parameters, assigned to variables, etc.

// isLessThan5 :: Number -> Boolean
const isLessThan5 = x => x < 5

filter(
  isLessThan5, 
  [1, 3, 6, 8]
)
// -> [1, 3]

Higher Order Functions

Functions take and can return functions.

First class function support enables higher order functions- functions that work on other functions, meaning that they take one or more functions as an argument and can also return a function.

const getServerStuff = (callback) => {
  return ajaxCall((json) => {
    return callback(json)
  })
}

// ... is the same as ...

const getServerStuff = ajaxCall;

Higher Order Functions

const getServerStuff = (callback) => {
  return ajaxCall((json) => {
    return callback(json)
  })
}

const getServerStuff = (callback) => {
  return ajaxCall(callback)
}

const getServerStuff = ajaxCall

Okay, back to the breakdown!

Filtering For Active Users

import { pipe, filter, map, pipe, pick, trim, length, values, sum } from 'ramda'

const users = [
  { active: true, first: 'Rob   ', last: '   Hilgefort ' }, // 12
  { active: true, first: 'John  ', last: ' Doe' }, // 7
  { active: false, first: '  Jane', last: 'Smith   ' },  // 9
  { active: true, first: 'Jesselin  ', last: ' Alexandra ' }, // 17
]

// User :: { active: Bool, first: String, last: String }
// sumNameLength :: [User] -> Number
const sumNameLength = pipe(
  filter(
    propEq('active', true)
  ),
  map(pipe(
    pick(['first', 'last']),
    map(
      pipe(trim, length)
    ),
    values,
    sum,
  )),
  sum,
)

sumNameLength(users) // 36

We've created an abstraction for `filter`, let's look at the predicate (condition) we're passing to it to select only the users which have a prop `active` equal to `true`.

Let's try write our own version of this function which is looking to find a property which equals a value.

`propEq` Predicate

filter(
  (user) => user.active === true,
  users
)

const isUserActive = 
  (user) => user.active === true
filter(
  user => isUserActive(user),
  users
)

const isActive = 
  (data) => data.active === true
filter(
  user => isActive(user),
  users
)

const isPropTrue = 
  (prop, data) => data[prop] === true
filter(
  user => isPropTrue('active', user),
  users
)

const propEq = 
  (prop, val, data) => data[prop] === val
filter(
  user => propEq('active', true, user),
  users
)

Works, but not reusable

We can name it, but it could apply to more than users

Nice, but we could be flexible to other props

While we're at it, we may as well make it fully flexible/reusable

✅, but we've learned that passing data through is noisy...

// User :: { active: Bool, first: String, last: String }
// sumNameLength :: [User] -> Number
const sumNameLength = pipe(
  filter(
    propEq('active', true)
  ),
  map(pipe(
    pick(['first', 'last']),
    map(
      pipe(trim, length)
    ),
    values,
    sum,
  )),
  sum,
)

What can we do to `propEq` to make this possible?

const propEq = 
  (prop, val, data) => data[prop] === val

const getServerStuff = (callback) => {
  return ajaxCall((json) => {
    return callback(json)
  })
}

// ... is the same as ...

const getServerStuff = ajaxCall;

Can we apply this HOC principle to reduce code and not name the data we're acting on?

So what's going on here?

`propEq` Predicate

// propEq :: 
//   (String, Any) -> Object -> Boolean
const propEq = (prop, val) => data =>
  data[prop] === val

We can build our function to return a function after providing the first two arguments.

`propEq` Predicate

Now we can provide the information we care about, and let `filter` fill in the rest.

// User :: { active: Bool, first: String, last: String }
// sumNameLength :: [User] -> Number
const sumNameLength = pipe(
  filter(
    propEq('active', true)
  ),
  map(pipe(
    pick(['first', 'last']),
    map(
      pipe(trim, length)
    ),
    values,
    sum,
  )),
  sum,
)

FP Topics

1️⃣ Tools

Higher Order Functions
Currying
Composition

2️⃣ Rules

Purity
Immutability
No Side Effects

3️⃣ Concepts

Declarative
First Class Functions
Point Free

const double = (x) => x * 2

[1,2,3,4,5].map(
  (number) => double(number)
)
// [2,4,6,8,10]



// ... is the same as ...



const double = (x) => x * 2

[1,2,3,4,5].map(double)
// [2,4,6,8,10]

No intermediate state.

Pointfree style means never having to say your data. Functions never mention the data upon which they operate.

Pointfree code can help us remove needless names and keep us concise and generic.

Point Free

What about non unary functions like our `propEq` function?

(Function arity refers to the number of arguments a function takes)

Non Unary Function

// propEq :: 
//   (String, Any) -> Object -> Boolean
const propEq = (prop, val) => data =>
  data[prop] === val

const add = x => y => z => 
  x + y + z

add(1)(2)(3) // 6
add(1, 2, 3) // <Function>

Manual Currying refers to function interfaces that expect their arguments one at a time.

You can call a function with fewer arguments than it expects. It returns a function that takes the remaining arguments. Because of this, it is critical that your data be supplied as the final argument.

Manual Currying

When we left our third argument out, to be filled in later, we curried our function!

import { curry } from 'ramda'

const add = curry(
  (x, y, z) => x + y + z
)

add(1, 2, 3) // 6
add(1)(2)(3) // 6
add(1, 2)(3) // 6
add(1)(2, 3) // 6

Many functional libraries provide a `curry` function which allow functions to be called like a normal function if desired. This is called Auto Currying.

When called with fewer than the expected arguments, a function is returned waiting for the remaining arguments.

Auto Currying

const add = x => y => z => 
  x + y + z

const add12 = add(10)(2)

add12(1) // 13
add12(8) // 20
add12(12) // 24

Back To The Breakdown

import { pipe, filter, map, pipe, pick, trim, length, values, sum } from 'ramda'

const users = [
  { active: true, first: 'Rob   ', last: '   Hilgefort ' }, // 12
  { active: true, first: 'John  ', last: ' Doe' }, // 7
  { active: false, first: '  Jane', last: 'Smith   ' },  // 9
  { active: true, first: 'Jesselin  ', last: ' Alexandra ' }, // 17
]

// User :: { active: Bool, first: String, last: String }
// sumNameLength :: [User] -> Number
const sumNameLength = pipe(
  filter(
    propEq('active', true)
  ),
  map(pipe(
    pick(['first', 'last']),
    map(
      pipe(trim, length)
    ),
    values,
    sum,
  )),
  sum,
)

sumNameLength(users) // 36

Now that we've filtered, we need to get the combined length of the "first" and "last" props for each user.

So what's this `pipe` all about?

Let's take this simpler example.

Sanitizing The Name

const sumNameLength = pipe(
  filter(
    propEq('active', true)
  ),
  map(pipe(
    pick(['first', 'last']),
    map(
      pipe(trim, length)
    ),
    values,
    sum,
  )),
  sum,
)

This could look like this:

After selecting the props we care about, we need to find their true length.

const { ..., trim, length } from 'ramda'

const sumNameLength = pipe(
  filter(
    propEq('active', true)
  ),
  map(pipe(
    pick(['first', 'last']),
    map(
      (val) => {
        const trimmed = trim(val)
        const valLength = length(trimmed)
        return valLength
      }
    ),
    values,
    sum,
  )),
  sum,
)

Sanitizing The Name

There's intermediate state that distracts from the aim.

map(
  (val) => {
    const trimmed = trim(val)
    const valLength = length(trimmed)
    return valLength
  }
)

map(
  (val) => length(trim(val))
)

map(
  (val) => compose(length, trim)(val)
)

map(
  compose(length, trim)
)

Better, but It's hard to see the data we're acting on.

We can compose these functions together!

And then it's easy to see that we can make this point-free.

FP Topics

1️⃣ Tools

Higher Order Functions
Currying
Composition

2️⃣ Rules

Purity
Immutability
No Side Effects

3️⃣ Concepts

Declarative
First Class Functions
Point Free

// compose :: 
//   (Function, Function) -> 
//     Any a -> 
//     Any b
const compose = (f, g) => x => f(g(x))

const add1 = x => x + 1
const add2 = compose(add1, add1)

add2(2) // 4
add2(5) // 7
add2(10) // 12

Functions built from functions.

Function composition is the process of combining two or more functions in order to produce a new function.

For example, the composition `f . g` (the dot means “composed with”) is equivalent to `f(g(x))` in JavaScript.

Composition

🎉 Full Breakdown 🎉

import { pipe, filter, map, pipe, pick, trim, length, values, sum } from 'ramda'

const users = [
  { active: true, first: 'Rob   ', last: '   Hilgefort ' }, // 12
  { active: true, first: 'John  ', last: ' Doe' }, // 7
  { active: false, first: '  Jane', last: 'Smith   ' },  // 9
  { active: true, first: 'Jesselin  ', last: ' Alexandra ' }, // 17
]

// User :: { active: Bool, first: String, last: String }
// sumNameLength :: [User] -> Number
const sumNameLength = pipe(
  filter(propEq('active', true)), // [User]
  map(pipe(
    pick(['first', 'last']),      // { first: String, last: String }
    map(pipe(trim, length)),      // { first: Number, last: Number } 
    values,                       // [Number]
    sum,                          // Number
  )),                             // [Number]
  sum,                            // Number
)

sumNameLength(users) // 36

FP Rules

FP Topics

1️⃣ Tools

Higher Order Functions
Currying
Composition

2️⃣ Rules

Purity
Immutability
No Side Effects

3️⃣ Concepts

Declarative
First Class Functions
Point Free

Purity

No outside scope.

Always returns a value.

// Impure
const maxNames = 5
const isValidNames = names => {
  return names.length <= maxNames
}
isValidNames(names) // false

const names = [
  'Michael', 'Erin', 'Dylan',
  'Wes', 'Bao', 'Taron',
]

// Impure
let count
const getNamesCount = names => {
  count = names.length
}
getNamesCount(names)
count // 6

// Pure
const isValidNames = names => {
  const maxNames = 5
  return names.length <= maxNames
}
isValidNames(names) // false

// Pure
const getNamesCount = names => names.length
const count = getNamesCount(names)
count // 6

Immutability ❌

Mutations can lead to inconsistent behavior and are hard to reason about.

Mutating shared state complicates debugging and reasoning about code.

// Given the following
const foo = { val: 2 }

const addOneObjVal = () => foo.val += 1
const doubleObjVal = () => foo.val *= 2

// Has a different effect on each call

addOneObjVal() // { val: 3 }
addOneObjVal() // { val: 4 }
addOneObjVal() // { val: 5 }
addOneObjVal() // { val: 6 }

// The order of execution changes
// the output of the function

addOneObjVal() // { val: 3 }
doubleObjVal() // { val: 6 }

// `foo` is reset to original

doubleObjVal() // { val: 4 }
addOneObjVal() // { val: 5 }

Immutability ✅

Objects can’t be modified after it’s created.

Immutability is a central concept of functional programming because without it, the data flow in your program is lossy. State history is abandoned, and strange bugs can creep into your software.

import { merge } from 'ramda'

// Given the following
const foo = { val: 2 }

const addOneObjVal = 
  x => merge(x, { val: x.val + 1})
const doubleObjVal =
  x => merge(x, { val: x.val * 2})

addOneObjVal(foo) // { val: 3 }
addOneObjVal(foo) // { val: 3 }
addOneObjVal(foo) // { val: 3 }

doubleObjVal(foo) // { val: 4 }
doubleObjVal(foo) // { val: 4 }

doubleObjVal(addOneObjVal(foo))
// { val: 6 }

compose(doubleObjVal, addOneObjVal)(foo)
// { val: 6 }

Resources

This talk was heavily inspired by the following resources.

If you liked this talk and/or want to learn more, these are some of my favorite links to give out.